9.7: 更高的根源
- Page ID
- 204429
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
在本节结束时，您将能够：
- 简化根数较高的表达式
- 使用 Product 属性简化具有较高根系的表达式
- 使用 Quotient 属性简化具有较高根系的表达式
- 加上和减去更高的根
简化具有较高根系的表达式
到目前为止，在本章中，我们已经使用了平方和平方根。 现在，我们将扩大工作范围，将更高的权力和更高的根源包括在内。
让我们先回顾一些词汇。
\[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]
术语 “平方” 和 “立方体” 来自正方形面积和立方体体积的公式。
如果有一张表，列出从 −5to5 的整数的幂会很有帮助。 参见图\(\PageIdnex{1}\)。
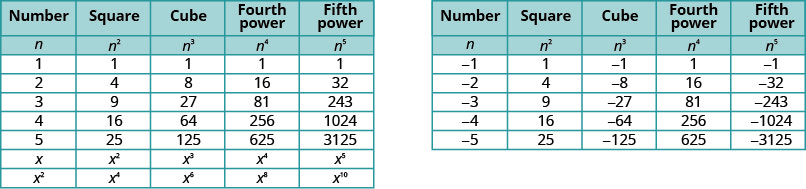
注意图中的标志\(\PageIndex{1}\)。 当然，所有正数的幂都是正数。 但是当我们有一个负数时，偶数幂是正数，奇数次方是负数。 我们将在下面复制带有 −2 幂的行，以帮助你看清这一点。
在本章前面，我们定义了数字的平方根。
if\(n^2=m\)，则 n 是 m 的平方根。
我们用这个表示法\(\sqrt{m}\)来表示主平方根。 所以\(\sqrt{m} \ge 0\)总是这样。
现在，我们将把定义扩展到更高的根源。
if\(b^n=a\)，则 b 是数字 a 的第 n 个根。
写入了 a 的第 n 个根的主体\(\sqrt[n]{a}=b\)
n 被称为激进的索引。
我们不为平方根写索引。 就像我们使用 “cubed” 这个词一样\(b^3\)，我们使用 “cube root” 一词来表示\(\sqrt[3]{a}\)。
我们参考图\(\PageIndex{1}\)是为了帮助我们找到更高的根源。
\[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]
我们可以有一个负数的偶数根吗？ 不。 我们知道负数的平方根不是实数。 任何偶数根也是如此。 负数的偶数根不是实数。 负数的奇数根是实数。
当 n 是偶数并且
- \(a\ge 0\)，那么\(\sqrt[n]{a}\)是一个实数
- \(a < 0\)，那么\(\sqrt[n]{a}\)不是实数
当 n 是奇数时，\(\sqrt[n]{a}\)是 a 的所有值的实数。
简化：
- \(\sqrt[3]{8}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)。
- 回答
-
1。 \(\sqrt[3]{8}\) 由于\((2)^3=8\)。 2 2。 \(\sqrt[4]{81}\) 由于\((3)^4=81\)。 3 3。 \(\sqrt[5]{32}\) 由于\((2)^5=32\)。 2
简化：
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{243}\)。
- 回答
-
- 3
- 4
- 3
简化：
- \(\sqrt[3]{1000}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{32}\)。
- 回答
-
- 10
- 2
- 2
简化：
- \(\sqrt[3]{−64}\)
- \(\sqrt[4]{−16}\)
- \(\sqrt[5]{−243}\)。
- 回答
-
1。 \(\sqrt[3]{−64}\) 由于\((−4)^3=−64\)。 −4 2。 \(\sqrt[4]{−16}\) 想想，\((?)^4=−16\).没有提高到第四次幂的实数是正数。 不是实数。 3。 \(\sqrt[5]{−243}\) 由于\((−3)^5=−243\)。 −3
简化：
- \(\sqrt[3]{−125}\)
- \(\sqrt[4]{−16}\)
- \(\sqrt[5]{−32}\)。
- 回答
-
- −5
- 不是真的
- −2
简化：
- \(\sqrt[3]{−216}\)
- \(\sqrt[4]{−81}\)
- \(\sqrt[5]{−1024}\)。
- 回答
-
- −6
- 不是真的
- −4
数字的奇数根可以是正数也可以是负数。 我们已经看见了\(\sqrt[3]{−64}=−4\)。
但是非负数的偶数根总是非负数，因为我们取主数 n 个根。
假设我们从 a=−5 开始。
\[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]
我们怎样才能确保 −5 的第四个根提高到第四次方，\((−5)^4\)即 5？ 我们将在以下属性中看到。
对于任何整数\(n \ge 2\)，
\[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]
当我们取一个表达式的偶数根时，我们必须使用绝对值符号，其中一个变量是激进的。
简化：
- \(\sqrt{x^2}\)
- \(\sqrt[3]{n^3}\)
- \(\sqrt[4]{p^4}\)
- \(\sqrt[5]{y^5}\)。
- 回答
-
我们使用绝对值来确保得到正根。
1。 \(\sqrt{x^2}\) 从那\((x)^2=x^2\)以后，我们想要积极的根源。 |x| 2。 \(\sqrt[3]{n^3}\) 由于\((n)^3=n^3\)。 它是一个奇数根，因此不需要绝对值符号。 n 3。 \(\sqrt[4]{p^4}\) 从那\((p)^4=p^4\)以后，我们想要积极的根源。 |p| 4。 \(\sqrt[5]{y^5}\) 由于\((y)^5=y^5\)。 它是一个奇数根，因此不需要绝对值符号。 y
简化：
- \(\sqrt{b^2}\)
- \(\sqrt[3]{w^3}\)
- \(\sqrt[4]{m^4}\)
- \(\sqrt[5]{q^5}\)。
- 回答
-
- |b|
- w
- |m|
- q
简化：
- \(\sqrt{y^2}\)
- \(\sqrt[3]{p^3}\)
- \(\sqrt[4]{z^4}\)
- \(\sqrt[5]{q^5}\)
- 回答
-
- |y|
- p
- |z|
- q
简化：
- \(\sqrt[3]{y^{18}}\)
- \(\sqrt[4]{z^8}\)。
- 回答
-
1。 \(\sqrt[3]{y^{18}}\) 由于\((y^6)^3=y^18\)。 \(\sqrt[3]{(y^6)^3}\) \(y^6\) 2。 \(\sqrt[4]{z^8}\) 由于\((z^2)^4=z^8\)。 \(\sqrt[4]{(z^2)^4}\) 由于\(z^2\)是正数，因此我们不需要绝对值符号。 \(z^2\)
简化：
- \(\sqrt[4]{u^{12}}\)
- \(\sqrt[3]{v^{15}}\)。
- 回答
-
- \(u^3\)
- \(v^5\)
简化：
- \(\sqrt[5]{c^{20}}\)
- \(\sqrt[6]{d^{24}}\)。
- 回答
-
- \(c^4\)
- \(d^4\)
简化：
- \(\sqrt[3]{64p^6}\)
- \(\sqrt[4]{16q^{12}}\)。
- 回答
-
1。 \(\sqrt[3]{64p^6}\) 重写\(64p^6\)为\((4p^2)^3\)。 \(\sqrt[3]{(4p^2)^3}\) 取立方体根。 \(4p^2\) 2。 \(\sqrt[4]{16q^{12}}\) 将激进分子重写为第四种力量。 \(\sqrt[4]{(2q^3)^4}\) 取第四根根。 \(2|q^3|\)
简化：
- \(\sqrt[3]{27x^{27}}\)
- \(\sqrt[4]{81q^{28}}\)。
- 回答
-
- \(3x^9\)
- \(3∣q^7∣\)
简化：
- \(\sqrt[3]{125p^9}\)
- \(\sqrt[5]{243q^{25}}\)
- 回答
-
- \(5p^3\)
- \(3q^5\)
使用 product 属性简化具有较高根系的表达式
我们将简化具有较高根的表达式，其方式与简化平方根表达式的方式大致相同。 如果第 n 个根没有因子，则将其视为简化\(m^n\)。
\(\sqrt[n]{a}\)如果 a 没有因子为，则视为简化\(m^n\)。
我们将把平方根的乘积属性概括为包括任何整数根\(n \ge 2\).
\(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)和\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
wh\(\sqrt[n]{a}\) en\(\sqrt[n]{b}\) and 是实数，对于任何整数\(n \ge 2\)
简化：
- \(\sqrt[3]{x^4}\)
- \(\sqrt[4]{x^7}\)。
- 回答
-
1。
\(\sqrt[3]{x^4}\) 使用最大的完美立方体因子将 radicand 重写为产品。 \(\sqrt[3]{x^3·x}\) 将激进改写为两个激进的乘积。 \(\sqrt[3]{x^3}·\sqrt[3]{x}\) 简化。 \(x\sqrt[3]{x}\) 2。 \(\sqrt[4]{x^7}\) 使用最大完美第四功率因数将 radicand 重写为产品。 \(\sqrt[4]{x^4·x^3}\) 将激进改写为两个激进的乘积。 \(\sqrt[4]{x^4}·\sqrt[4]{x^3}\) 简化。 \(|x|\sqrt[4]{x^3}\)
简化：
- \(\sqrt[4]{y^6}\)
- \(\sqrt[3]{z^5}\)。
- 回答
-
- \(|y∣\sqrt[4]{y^2}\)
- \(z\sqrt[3]{z^2}\)
简化：
- \(\sqrt[5]{p^8}\)
- \(\sqrt[6]{q^{13}}\)。
- 回答
-
- \(p\sqrt[5]{p^3}\)
- \( q^2\sqrt[6]{q}\)
简化：
- \(\sqrt[3]{16}\)
- \(\sqrt[4]{243}\)。
- 回答
-
1。 \(\sqrt[3]{16}\) \(\sqrt[3]{2^4}\) 使用最大的完美立方体因子将 radicand 重写为产品。 \(\sqrt[3]{2^3·2}\) 将激进改写为两个激进的乘积。 \(\sqrt[3]{2^3}·\sqrt[3]{2}\) 简化。 \(2\sqrt[3]{2}\) 2。 \(\sqrt[4]{243}\) \(\sqrt[4]{3^5}\) 使用最大完美第四功率因数将 radicand 重写为产品。 \(\sqrt[4]{3^4·3}\) 将激进改写为两个激进的乘积。 \(\sqrt[4]{3^4}·\sqrt[4]{3}\) 简化。 \(3\sqrt[4]{3}\)
简化：
- \(\sqrt[3]{81}\)
- \(\sqrt[4]{64}\)。
- 回答
-
- \(3\sqrt[3]{3}\)
- \(2\sqrt[4]{4}\)
简化：
- \(\sqrt[3]{625}\)
- \(\sqrt[4]{729}\)。
- 回答
-
- \(5\sqrt[3]{5}\)
- \(3\sqrt[4]{9}\)
在取一个表达式的偶数根时，别忘了使用绝对值符号，其中的变量是激进的。
简化：
- \(\sqrt[3]{24x^7}\)
- \(\sqrt[4]{80y^{14}}\)。
- 回答
-
1。 \(\sqrt[3]{24x^7}\) 使用完美的立方体因子将 radicand 重写为产品。 \(\sqrt[3]{2^{3}x^{6}·3x}\) 将激进改写为两个激进的乘积。 \(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\) 将第一个 radicand 重写为\((2x^2)^3\) \(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\) 简化。 \(2x^2\sqrt[3]{3x}\) 2。 \(\sqrt[4]{80y^{14}}\) 使用完美的第四次功率因数将 radicand 重写为产品。 \(\sqrt[4]{2^{4}y^{12}·5y^2}\) 将激进改写为两个激进的乘积。 \(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\) 将第一个 radicand 重写为\((2y^3)^4\) \(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\) 简化。 \(2|y^3|\sqrt[4]{5y^2}\)
简化：
- \(\sqrt[3]{54p^[10}]\)
- \(\sqrt[4]{64q^{10}}\)。
- 回答
-
- \(3p^3\sqrt[3]{2p}\)
- \(2q^2\sqrt[4]{4q^2}\)
简化：
- \(\sqrt[3]{128m^{11}}\)
- \(\sqrt[4]{162n^7}\)。
- 回答
-
- \(4m^3\sqrt[3]{2m^2}\)
- \(3|n|\sqrt[4]{2n^3}\)
简化：
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−16}\)。
- 回答
-
1。 \(\sqrt[3]{−27}\) 使用完美的立方体因子将 radicand 重写为产品。 \(\sqrt[3]{(−3)^3}\) 取立方体根。 −3 2。 \(\sqrt[4]{−16}\) 哪里没有实数 n\(n^4=−16\)。 不是实数。
简化：
- \(\sqrt[3]{−108}\)
- \(\sqrt[4]{−48}\)。
- 回答
-
- \(−3\sqrt[3]{4}\)
- 不是真的
简化：
- \(\sqrt[3]{−625}\)
- \(\sqrt[4]{−324}\)。
- 回答
-
- \(−5\sqrt[3]{5}\)
- 不是真的
使用 Quotient 属性简化具有较高根系的表达式
我们可以像简化平方根一样用商来简化较高的根。 首先，我们简化激进内部的所有分数。
简化：
- \(\sqrt[3]{\frac{a^8}{a^5}}\)
- \(\sqrt[4]{\frac{a^{10}}{a^2}}\)。
- 回答
-
1。
\(\sqrt[3]{\frac{a^8}{a^5}}\) 首先简化激进部分下的分数。 \(\sqrt[3]{a^3}\) 简化。 一个 2。 \(\sqrt[4]{\frac{a^{10}}{a^2}}\) 首先简化激进部分下的分数。 \(\sqrt[4]{a^8}\) 使用完美的第四次功率因数重写 radicand。 \(\sqrt[4]{(a^2)^4}\) 简化。 \(a^2\)
简化：
- \(\sqrt[4]{\frac{x^7}{x^3}}\)
- \(\sqrt[4]{\frac{y^{17}}{y^5}}\)。
- 回答
-
- |x|
- \(y^3\)
简化：
- \(\sqrt[3]{\frac{m^{13}}{m^7}}\)
- \(\sqrt[5]{\frac{n^{12}}{n^2}}\)。
- 回答
-
- \(m^2\)
- \(n^2\)
以前，我们使用 Quotient 属性 “反向” 来简化平方根。 现在，我们将对公式进行概括以包括更高的根。
\(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)和\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
什么时候\(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b \ne 0\), and for any integer \(n \ge 2\)
简化：
- \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
- \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
- 回答
-
1。 \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\) 两个 radicand 都不是完美的立方体，所以使用 Quotient Property 写成一个激进。 \(\sqrt[3]{\frac{−108}{2}}\) 简化激进下方的分数。 \(\sqrt[3]{−54}\) 使用完美的立方体因子将 radicand 重写为产品。 \(\sqrt[3]{(−3)^3·2}\) 将激进改写为两个激进的乘积。 \(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\) 简化。 \(−3\sqrt[3]{2}\) 2。 \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\) 两个 radicand 都不是完美的第四次方，所以使用 Quotient Property 写成一个激进分子 \(\sqrt[4]{\frac{96x^7}{3x^2}}\) 简化激进下方的分数。 \(\sqrt[4]{32x^5}\) 使用完美的第四次功率因数将 radicand 重写为产品。 \(\sqrt[4]{2^{4}x^4·2x}\) 将激进改写为两个激进的乘积。 \(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\) 简化。 \(2|x|\sqrt[4]{2x}\)
简化：
- \(\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}\)
- \(\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}\)
- 回答
-
- 不是真的
- \(3|m|\sqrt[4]{2m^2}\)
简化：
- \(\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}\)
- \(\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}\)。
- 回答
-
- −4
- \(3|n|\sqrt[4]{2}\)
如果部首内部的分数无法简化，我们使用 Quotient Property 的第一种形式将表达式重写为两个部首的商。
简化：
- \(\sqrt[3]{\frac{24x^7}{y^3}}\)
- \(\sqrt[4]{\frac{48x^{10}}{y^8}}\)。
- 回答
-
1。 \(\sqrt[3]{\frac{24x^7}{y^3}}\) 基数中的分数无法简化。 使用商属性写成两个部首。 \(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\) 使用完美的立方体因子将每个 radicand 重写为产品。 \(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\) 将分子重写为两个自由基的乘积。 \(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\) 简化。 \(\frac{2x^2\sqrt[3]{3x}}{y}\) 2。 \(\sqrt[4]{\frac{48x^{10}}{y^8}}\) 基数中的分数无法简化。 使用商属性写成两个部首。 \(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\) 使用完美的立方体因子将每个 radicand 重写为产品。 \(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\) 将分子重写为两个自由基的乘积。 \(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\) 简化。 \(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)
简化：
- \(\sqrt[3]{\frac{108c^{10}}{d^6}}\)
- \(\sqrt[4]{\frac{80x^{10}}{y^5}}\)。
- 回答
-
- \(\frac{3c^3\sqrt[3]{4c}}{d^2}\)
- \(\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}\)
简化：
- \(\sqrt[3]{\frac{40r^3}{s}}\)
- \(\sqrt[4]{\frac{162m^{14}}{n^{12}}}\)
- 回答
-
- \(r\sqrt[3]{\frac{40}{s}}\)
- \(\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}\)
加上和减去更高的根
我们可以加上和减去更高的根，就像我们加上和减去平方根一样。 首先，我们给出了类似激进分子的正式定义。
具有相同索引和相同基数的激进被称为激进。
就像激进分子有相同的指数和相同的基数。
- \(9\sqrt[4]{42x}\)\(−2\sqrt[4]{42x}\)而且就像激进分子。
- \(5\sqrt[3]{125x}\)而且\(6\sqrt[3]{125y}\)不像激进分子。 激进分子是不同的。
- \(2\sqrt[5]{1000q}\)而且\(−4\sqrt[4]{1000q}\)不像激进分子。 指数不同。
我们像激进项一样添加和减去，其方式与相似项相加和减去的方式相同。 我们可以添加\(9\sqrt[4]{42x}+(−2\sqrt[4]{42x})\)，结果是\(7\sqrt[4]{42x}\)。
简化：
- \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
- \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
- 回答
-
1。 \(\sqrt[3]{4x}+\sqrt[3]{4x}\) 自由基就像，所以我们加上系数 \(2\sqrt[3]{4x}\) 2。 \(4\sqrt[4]{8}−2\sqrt[4]{8}\) 自由基就像，所以我们减去系数。 \(2\sqrt[4]{8}\)
简化：
- \(\sqrt[5]{3x}+\sqrt[5]{3x}\)
- \(3\sqrt[3]{9}−\sqrt[3]{9}\)
- 回答
-
- \(2\sqrt[5]{3x}\)
- \(2\sqrt[3]{9}\)
简化：
- \(\sqrt[4]{10y}+\sqrt[4]{10y}\)
- \(5\sqrt[6]{32}−3\sqrt[6]{32}\)。
- 回答
-
- \(2\sqrt[4]{10y}\)
- \(2\sqrt[6]{32}\)
当一个表达式看起来不像激进分子时，我们将首先简化每个部首。 有时候，这会导致激进分子相似的表情。
简化：
- \(\sqrt[3]{54}−\sqrt[3]{16}\)
- \(\sqrt[4]{48}+\sqrt[4]{243}\)。
- 回答
-
1。 \(\sqrt[3]{54}−\sqrt[3]{16}\) 使用完美立方因子重写每个 radicand。 \(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\) 重写完美的立方体。 \(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\) 尽可能简化激进分子。 \(3\sqrt[3]{2}−2\sqrt[3]{2}\) 像激进分子一样结合。 \(\sqrt[3]{2}\) 2。 \(\sqrt[4]{48}+\sqrt[4]{243}\) 使用完美的第四个功率因数重写。 \(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\) 使用完美的立方体因子将每个 radicand 重写为产品。 \(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\) 将分子重写为两个自由基的乘积。 \(2\sqrt[4]{3}+3\sqrt[4]{3}\) 简化。 \(5\sqrt[4]{3}\)
简化：
- \(\sqrt[3]{192}−\sqrt[3]{81}\)
- \(\sqrt[4]{32}+\sqrt[4]{512}\)。
- 回答
-
- \(\sqrt[3]{3}\)
- \(6\sqrt[4]{2}\)
简化：
- \(\sqrt[3]{108}−\sqrt[3]{250}\)
- \(\sqrt[5]{64}+\sqrt[5]{486}\)。
- 回答
-
- \(−\sqrt[3]{2}\)
- \(5\sqrt[5]{2}\)
简化：
- \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
- \(\sqrt[4]{162y^9}+\sqrt[4]{512y^5}\)。
- 回答
-
1。 \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\) 使用完美立方因子重写每个 radicand。 \(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\) 重写完美的立方体。 \(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\) 尽可能简化激进分子。 \(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\) 2。 \(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\) 使用完美的第四个功率因数重写。 \(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\) 使用完美的立方体因子将每个 radicand 重写为产品。 \(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\) 将分子重写为两个自由基的乘积。 \(3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}\)
简化：
- \(\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}\)
- \(\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}\)。
- 回答
-
- \(2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}\)
- \(3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}\)
简化：
- \(\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}\)
- \(\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}\)。
- 回答
-
- \(2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}\)
- \(2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}\)
- 简化更高的根源
- 添加/减去索引较高的根
关键概念
- 的属性
- \(\sqrt[n]{a}\)当 n 是偶数并且
- \(a \ge 0\)，那么\(\sqrt[n]{a}\)是一个实数
- \(a < 0\)，那么\(\sqrt[n]{a}\)不是实数
- 当 n 是奇数时，\(\sqrt[n]{a}\)是 a 的所有值的实数。
- 对于任何整数\(n \ge 2\)，当 n 为奇数时\(\sqrt[n]{a^n}=a\)
- 对于任何整数\(n \ge 2\)，当 n 为偶数时\(\sqrt[n]{a^n}=|a|\)
- \(\sqrt[n]{a}\)如果 a 没有因子为，则视为简化\(m^n\)。
- \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)和\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
- \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)和\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
- 要像自由基一样进行组合，只需将系数相加或减去即可，同时保持基数不变。
词汇表
- n 个数字的根
- if\(b^n=a\)，那么 b 是 a 的第 n 个根。
- 根上的主体
- 写入了 a 的根中的主体\(\sqrt[n]{a}\)。
- 索引
- \(\sqrt[n]{a}\)n 被称为激进的索引。
- 像激进分子一样
- 具有相同索引和相同基数的激进被称为激进。