6.7: 整数指数和科学记数法

学习目标

在本节结束时，您将能够：

• 使用负指数的定义
• 使用整数指数简化表达式
• 从十进制记数法转换为科学记数法
• 将科学记数法转换为十进制形式
• 使用科学记数法进行乘法和除法

注意

在开始之前，请参加这个准备测验。

1. 数字 64891 中 6 的位值是多少？
   如果您错过了此问题，请查看练习 1.2.1。
2. 将十进制命名为：0.0012。
   如果您错过了此问题，请查看练习 1.8.1。
3. 减去：5− (−3)。
   如果您错过了此问题，请查看练习 1.4.33。

使用负指数的定义

我们看到，本章前面介绍的指数的商属性有两种形式，具体取决于分子还是分母中的指数较大。

指数的商属性

如果 a 是实数\(a\neq0\)，而 m 和 n 是整数，那么

\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]

和

\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]

如果不管哪个指数更大，我们都只减去指数怎么办？

让我们考虑一下\(\dfrac{x^{2}}{x^{5}}\)。

我们从分子中的指数中减去分母中的指数。

\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]

我们还可以\(\dfrac{x^{2}}{x^{5}}\)通过划分常见因素来进行简化：

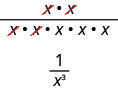
这意味着这一点\(x^{-3}=\dfrac{1}{x^{3}}\)，它使我们得出了负指数的定义。

定义：负指数

如果 n 是一个整数\(a\neq 0\)，那么\(a^{-n}=\dfrac{1}{a^{n}}\)

负指数告诉我们，我们可以通过取基数的倒数然后更改指数的符号来重写表达式。

任何具有负指数的表达式都不被视为最简单的形式。 我们将使用负指数的定义和指数的其他属性来编写仅包含正指数的表达式。

例如，如果在简化了一个表达式之后我们最终得到了一个表达式\(x^{-3}\)，那么我们将再走一步来编写\(\dfrac{1}{x^{3}}\)。 当答案只有正指数时，它被认为是最简单的形式。

练习\(\PageIndex{1}\)

简化：

1. \(4^{-2}\)
2. \(10^{-3}\)

回答

1. \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
2. \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)

练习\(\PageIndex{2}\)

简化：

1. \(2^{-3}\)
2. \(10^{-7}\)

回答

1. \(\dfrac{1}{8}\)
2. \(\dfrac{1}{10^{7}}\)

练习\(\PageIndex{3}\)

简化：

1. \(3^{-2}\)
2. \(10^{-4}\)

回答

1. \(\dfrac{1}{9}\)
2. \(\dfrac{1}{10,000}\)

在练习中，\(\PageIndex{1}\)我们将一个整数提高到负指数。 当我们将分数提高到负指数时会发生什么？ 首先，我们来看看分子为一且分母是整数的分数会发生什么，该分数的分数会被提升到负指数。

\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)

这就产生了负指数的属性。

负指数的性质

如果 n 是一个整数\(a\neq 0\)，那么\(\dfrac{1}{a^{-n}}=a^{n}\)。

练习\(\PageIndex{4}\)

简化：

1. \(\dfrac{1}{y^{-4}}\)
2. \(\dfrac{1}{3^{-2}}\)

回答

1. \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
2. \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)

练习\(\PageIndex{5}\)

简化：

1. \(\dfrac{1}{p^{-8}}\)
2. \(\dfrac{1}{4^{-3}}\)

回答

1. \(p^{8}\)
2. 64

练习\(\PageIndex{6}\)

简化：

1. \(\dfrac{1}{q^{-7}}\)
2. \(\dfrac{1}{2^{-4}}\)

回答

1. \(q^{7}\)
2. 16

假设现在我们有一个分数提高到负指数。 让我们用我们对负指数的定义来引导我们找到一个新的属性。

\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)

为了从原始分数上升到负指数到最终结果，我们取了基数的倒数（分数），然后更改了指数的符号。

这使我们得出了商到负幂属性。

商到负指数属性

如果\(a\)和\(b\)是实数，\(a \neq 0, b \neq 0,\)并且\(n\)是整数，那么\(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)

练习\(\PageIndex{7}\)

简化：

1. \(\left(\dfrac{5}{7}\right)^{-2}\)
2. \(\left(-\dfrac{2 x}{y}\right)^{-3}\)

回答

1. \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
2. \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)

练习\(\PageIndex{8}\)

简化：

1. \(\left(\dfrac{2}{3}\right)^{-4}\)
2. \(\left(-\dfrac{6 m}{n}\right)^{-2}\)

回答

1. \(\dfrac{81}{16} \)
2. \(\dfrac{n^{2}}{36 m^{2}}\)

练习\(\PageIndex{9}\)

简化：

1. \(\left(\dfrac{3}{5}\right)^{-3}\)
2. \(\left(-\dfrac{a}{2 b}\right)^{-4}\)

回答

1. \(\dfrac{125}{27}\)
2. \(\dfrac{16 b^{4}}{a^{4}}\)

在用指数简化表达式时，我们必须小心谨慎地正确识别基数。

练习\(\PageIndex{10}\)

简化：

1. \((-3)^{-2}\)
2. \(-3^{-2}\)
3. \(\left(-\dfrac{1}{3}\right)^{-2}\)
4. \(-\left(\dfrac{1}{3}\right)^{-2}\)

回答

1. 这里的指数适用于以 −3 为基数。 \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
2. 这个表达式的\(-3^{-2}\)意思是 “找到相反\(3^{-2}\)的东西”。 这里的指数适用于以 3 为基数。 \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
3. 这里的指数适用于基数\(\left(-\dfrac{1}{3}\right)\)。 \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
4. 这个表达式的\(-\left(\dfrac{1}{3}\right)^{-2}\)意思是 “找到相反\(\left(\dfrac{1}{3}\right)^{-2}\)的东西”。 这里的指数适用于基数\(\left(\dfrac{1}{3}\right)\)。 \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)

练习\(\PageIndex{11}\)

简化：

1. \((-5)^{-2}\)
2. \(-5^{-2}\)
3. \(\left(-\dfrac{1}{5}\right)^{-2}\)
4. \(-\left(\dfrac{1}{5}\right)^{-2}\)

回答

1. \(\dfrac{1}{25}\)
2. \(-\dfrac{1}{25}\)
3. 25
4. −25

练习\(\PageIndex{12}\)

简化：

1. \((-7)^{-2}\)
2. \(-7^{-2}\)
3. \(\left(-\dfrac{1}{7}\right)^{-2}\)
4. \(-\left(\dfrac{1}{7}\right)^{-2}\)

回答

1. \(\dfrac{1}{49}\)
2. \(-\dfrac{1}{49}\)
3. 49
4. −49

我们必须谨慎遵守行动顺序。 在下一个示例中，部件 (a) 和 (b) 看起来相似，但结果不同。

练习\(\PageIndex{13}\)

简化：

1. 4\(\cdot 2^{-1}\)
2. \((4 \cdot 2)^{-1}\)

回答

1. \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
2. \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)

练习\(\PageIndex{14}\)

简化：

1. 6\(\cdot 3^{-1}\)
2. \((6 \cdot 3)^{-1}\)

回答

1. 2
2. \(\dfrac{1}{18}\)

练习\(\PageIndex{15}\)

简化：

1. 8\(\cdot 2^{-2}\)
2. \((8 \cdot 2)^{-2}\)

回答

1. 2
2. \(\dfrac{1}{256}\)

当变量升高为负指数时，我们应用定义的方式与处理数字的方式相同。 我们将假设所有变量都非零。

练习\(\PageIndex{16}\)

简化：

1. \(x^{-6}\)
2. \(\left(u^{4}\right)^{-3}\)

回答

1. \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
2. \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)

练习\(\PageIndex{17}\)

简化：

1. \(y^{-7}\)
2. \(\left(z^{3}\right)^{-5}\)

回答

1. \(\dfrac{1}{y^{7}}\)
2. \(\dfrac{1}{z^{15}}\)

练习\(\PageIndex{18}\)

简化：

1. \(p^{-9}\)
2. \(\left(q^{4}\right)^{-6}\)

回答

1. \(\dfrac{1}{p^{9}}\)
2. \(\dfrac{1}{q^{24}}\)

当有乘积和指数时，我们必须小心谨慎地将指数应用于正确的数量。 根据运算顺序，我们在应用指数之前简化了括号中的表达式。 我们将在下一个示例中看到它是如何工作的。

练习\(\PageIndex{19}\)

简化：

1. 5\(y^{-1}\)
2. \((5 y)^{-1}\)
3. \((-5 y)^{-1}\)

回答

1. \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
2. \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
3. \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)

练习\(\PageIndex{20}\)

简化：

1. 8\(p^{-1}\)
2. \((8 p)^{-1}\)
3. \((-8 p)^{-1}\)

回答

1. \(\dfrac{8}{p}\)
2. \(\dfrac{1}{8 p}\)
3. \(-\dfrac{1}{8 p}\)

练习\(\PageIndex{21}\)

简化：

1. 11\(q^{-1}\)
2. \((11 q)^{-1}-(11 q)^{-1}\)
3. \((-11 q)^{-1}\)

回答

1. \(\dfrac{11}{1 q}\)
2. \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
3. \(-\dfrac{1}{11 q}\)

对于负指数，商法则只需要一种形式\(\dfrac{a^{m}}{a^{n}}=a^{m-n},\)来表示\(a \neq 0\) 0。 当分母中的指数大于分子中的指数时，商的指数将为负。

使用整数指数简化表达式

我们在本章前面开发的所有带有整数指数的指数属性也适用于整数指数。 我们在这里重述它们以供参考。

指数属性的摘要

如果\(a\)和\(b\)是实数，并且\(m\)和\(n\)是整数，那么

\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)

练习\(\PageIndex{22}\)

简化：

1. \(x^{-4} \cdot x^{6}\)
2. \(y^{-6} \cdot y^{4}\)
3. \(z^{-5} \cdot z^{-3}\)

回答

1. \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
2. \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
3. \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)

练习\(\PageIndex{23}\)

简化：

1. \(x^{-3} \cdot x^{7}\)
2. \(y^{-7} \cdot y^{2}\)
3. \(z^{-4} \cdot z^{-5}\)

回答

1. \(x^{4}\)
2. \(\dfrac{1}{y^{5}}\)
3. \(\dfrac{1}{z^{9}}\)

练习\(\PageIndex{24}\)

简化：

1. \(a^{-1} \cdot a^{6}\)
2. \(b^{-8} \cdot b^{4}\)
3. \(c^{-8} \cdot c^{-7}\)

回答

1. \(a^{5}\)
2. \(\dfrac{1}{b^{4}}\)
3. \(\dfrac{1}{c^{15}}\)

在接下来的两个示例中，我们将首先使用 Commutative Property 将相同的变量组合在一起。 这使得在使用产品属性之前可以更轻松地识别相似的基础。

练习\(\PageIndex{25}\)

简化：\(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)

回答

\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)

练习\(\PageIndex{26}\)

简化：\(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)

回答

\(\frac{1}{p^3 q^3}\)

练习\(\PageIndex{27}\)

简化：\(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)

回答

\(\frac{1}{r^2 s^8}\)

如果单项式有数值系数，我们将系数相乘，就像我们之前所做的那样。

练习\(\PageIndex{28}\)

简化：\(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)

回答

\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)

练习\(\PageIndex{29}\)

简化：\(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)

回答

\(-\frac{12v^5}{u}\)

练习\(\PageIndex{30}\)

简化：\(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)

回答

\(\frac{30d^3}{c^8}\)

在接下来的两个示例中，我们将使用功率属性和乘积到功率属性。

练习\(\PageIndex{31}\)

简化：\(\left(6 k^{3}\right)^{-2}\)

回答

\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)

练习\(\PageIndex{32}\)

简化：\(\left(-4 x^{4}\right)^{-2}\)

回答

\(\frac{1}{16x^8}\)

练习\(\PageIndex{33}\)

简化：\(\left(2 b^{3}\right)^{-4}\)

回答

\(\frac{1}{16b^{12}}\)

练习\(\PageIndex{34}\)

简化：\(\left(5 x^{-3}\right)^{2}\)

回答

\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)

练习\(\PageIndex{35}\)

简化：\(\left(8 a^{-4}\right)^{2}\)

回答

\(\frac{64}{a^8}\)

练习\(\PageIndex{36}\)

简化：\(\left(2 c^{-4}\right)^{3}\)

回答

\(\frac{8}{c^{12}}\)

为了简化分数，我们使用商属性并减去指数。

练习\(\PageIndex{37}\)

简化：\(\dfrac{r^{5}}{r^{-4}}\)

回答

\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)

练习\(\PageIndex{38}\)

简化：\(\dfrac{x^{8}}{x^{-3}}\)

回答

\(x^{11}\)

练习\(\PageIndex{39}\)

简化：\(\dfrac{y^{8}}{y^{-6}}\)

回答

\(y^{14}\)

从十进制记数法转换为科学记数法

还记得使用整数和小数的位值吗？ 我们的数字系统以 10 的幂为基础。 我们使用数十、数百、数千等等。 我们的十进制数也基于十的幂——十分之一、百分之一、千分之一等等。 以数字 4,000 和 0.004 为例。 我们知道 4,000 表示\(4 \times 1,000\)，0.004 表示\(4 \times \dfrac{1}{1,000}\)。

如果我们将1000写成指数形式的十次方，我们可以用这种方式重写这些数字：

\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]

当一个数字写成两个数字的乘积时，其中第一个因子是大于或等于 1 但小于 10 的数字，第二个因子是以指数形式书写的 10 的乘方，则说它是用科学记数法写的。

科学记数法

数字的形式是用科学记数法表示的

\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]

在科学记数法中，习惯上使用\(\times\)乘法符号作为乘法符号，尽管我们避免在代数的其他地方使用这个符号。

如果我们看看小数点发生了什么，我们可以看到一种可以轻松地从十进制记数法转换为科学记数法的方法。

在这两种情况下，将小数点移动 3 位，得出介于 1 和 10 之间的第一个因子。

\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)

练习\(\PageIndex{40}\): HOW TO CONVERT FROM DECIMAL NOTATION TO SCIENTIFIC NOTATION

用科学记数法书写：37000。

回答

练习\(\PageIndex{41}\)

用科学记数法书写：96000。

回答

\(9.6 \times 10^{4}\)

练习\(\PageIndex{42}\)

用科学记数法书写：48300。

回答

\(4.83 \times 10^{4}\)

操作方法：从十进制记数法转换为科学记数法

1. 第 1 步。 移动小数点，使第一个因子大于或等于 1 但小于 10。
2. 第 2 步。 计算小数点移动的小数位数 n。
3. 第 3 步。 将数字写成 10 的乘积。
   如果原始号码是：
   • 大于 1，10 的次方将为 10 ⁿ。
   • 在 0 和 1 之间，10 的幂将^{为 10 −n}。
4. 第 4 步。 查看。

练习\(\PageIndex{43}\)

用科学记数法书写：0.0052。

回答

原始数字 0.0052 介于 0 和 1 之间，因此我们的负乘方为 10。

移动小数点得到 5.2，一个介于 1 和 10 之间的数字。
计算该点移动的小数位数。
以 10 的幂数写成 produce。
查看。
\(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\)
0.0052

练习\(\PageIndex{44}\)

用科学记数法书写：0.0078

回答

\(7.8 \times 10^{-3}\)

练习\(\PageIndex{45}\)

用科学记数法书写：0.0129

回答

\(1.29 \times 10^{-2}\)

将科学记数法转换为十进制形式

我们怎样才能从科学记数法转换为十进制形式？ 让我们来看看用科学记数法书写的两个数字，然后看看。

\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]

如果我们看一下小数点的位置，我们可以看到一种简单的方法可以将数字从科学记数法转换为十进制形式。

\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]

在这两种情况下，小数点都移动了 4 位。 当指数为正数时，小数向右移动。 当指数为负数时，小数点向左移动。

练习\(\PageIndex{46}\)

转换为十进制格式：\(6.2 \times 10^{3}\)

回答

练习\(\PageIndex{47}\)

转换为十进制格式：\(1.3 \times 10^{3}\)

回答

\(1,300\)

练习\(\PageIndex{48}\)

转换为十进制格式：\(9.25 \times 10^{4}\)

回答

\(92,500\)

这些步骤总结如下。

怎么做

将科学记数法转换为十进制形式。

要将科学记数法转换为十进制形式：

1. 第 1 步。 确定因子\(n\)上的指数\(10\)。
2. 第 2 步。 移动小数\(n\)位，必要时添加零。
   • 如果指数为正，则将小\(n\)数点向右移动。
   • 如果指数为负数，则将小\(|n|\)数点向左移动。
3. 第 3 步。 查看。

练习\(\PageIndex{49}\)

转换为十进制格式：\(8.9\times 10^{-2}\)

回答

确定因子\(n\)上的指数\(10\)。
由于指数为负，因此将小数点向左移动 2 位。
根据需要为占位符添加零。

练习\(\PageIndex{50}\)

转换为十进制格式：\(1.2 \times 10^{-4}\)

回答

\(0.00012\)

练习\(\PageIndex{51}\)

转换为十进制格式：\(7.5 \times 10^{-2}\)

回答

\(0.075\)

使用科学记数法进行乘法和除法

天文学家使用非常大的数字来描述宇宙中的距离以及恒星和行星的年龄。 化学家使用非常小的数字来描述原子的大小或电子上的电荷。 当科学家用非常大或非常小的数字进行计算时，他们使用科学记数法。 科学记数法提供了一种无需写大量零即可完成计算的方法。 我们将看到如何使用指数的属性来乘以和除以科学计数法中的数字。

练习\(\PageIndex{52}\)

乘。 以十进制形式写出答案：\(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)

回答

\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)

练习\(\PageIndex{53}\)

乘\((3\times 10^{6})(2\times 10^{-8})\)。 以十进制形式写出答案。

回答

\(0.06\)

练习\(\PageIndex{54}\)

乘\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\)。 以十进制形式写出答案。

回答

\(0.009\)

练习\(\PageIndex{55}\)

除以。 以十进制形式写出答案：\(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)

回答

\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)

练习\(\PageIndex{56}\)

除以十进制形式\(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\)写出答案。

回答

\(400,000\)

练习\(\PageIndex{57}\)

除以十进制形式\(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\)写出答案。

回答

\(20,000\)

媒体访问其他在线资源

访问这些在线资源以获取更多指导和使用整数指数和科学记数法进行练习：

• 负指数
• 科学记数法
• 科学记数法 2

关键概念

• 负指数的属性
  • 如果\(n\)是正整数\(a \ne 0\)，那么\(\dfrac{1}{a^{−n}}=a^n\)
    
• 商到负指数
  • 如果\(a\)和\(b\)是实数，\(b \ne 0\)并且\(n\)是整数，那么\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
    
• 要将科学记数法转换为十进制形式：
  1. 在因子\(n\)上确定指数\(10\)。
  2. 移动小数\(n\)位，必要时添加零。
     • 如果指数为正，则将小\(n\)数点向右移动。
     • 如果指数为负数，则将小\(|n|\)数点向左移动。
  3. 查看。
     
• 要将十进制转换为科学记数法，请执行以下操作：
  1. 移动小数点，使第一个因子大于或等于\(1\)但小于\(10\)。
  2. 计算小数点被移动的小数位数。\(n\)
  3. 将数字写成乘积，其次方为\(10\)。 如果原始号码是：
     • 大于\(1\)，\(10\)意志的力量是\(10^n\)
     • 介于\(0\)和之间\(1\)，\(10\)意志的力量是\(10^{−n}\)
  4. 查看。

词汇表

负指数

如果\(n\)是正整数\(a \neq 0\)，那么\(a^{-n}=\dfrac{1}{a^{n}}\)。

科学记数法

当数字的形式为 where\(a \geq 1\) 和 a<10 并且\(n\)是一个整数时\(a \times 10^{n}\)，用科学记数法表示。