4.7E:练习
- Page ID
- 204711
练习成就完美
验证两个变量中不等式的解
在以下练习中,确定每个有序对是否是给定不等式的解。
确定每个有序对是否是不等式的解\(y>x−1\):
- \((0,1)\)
- \((−4,−1)\)
- \((4,2)\)
- \((3,0)\)
- \((−2,−3)\)
确定每个有序对是否是不等式的解\(y>x−3\):
- \((0,0)\)
- \((2,1)\)
- \((−1,−5)\)
- \((−6,−3)\)
- \((1,0)\)
- 回答
-
- 是的
- 不
- 不
- 是的
- 不
确定每个有序对是否是不等式的解\(y<x+2\):
- \((0,3)\)
- \((−3,−2)\)
- \((−2,0)\)
- \((0,0)\)
- \((−1,4)\)
确定每个有序对是否是不等式的解\(y<x+5\):
- \((−3,0)\)
- \((1,6)\)
- \((−6,−2)\)
- \((0,1)\)
- \((5,−4)\)
- 回答
-
- 是的
- 不
- 不
- 是的
- 是的
确定每个有序对是否是不等式的解\(x+y>4\):
- \((5,1)\)
- \((−2,6)\)
- \((3,2)\)
- \((10,−5)\)
- \((0,0)\)
确定每个有序对是否是不等式的解\(x+y>2\):
- \((1,1)\)
- \((4,−3)\)
- \((0,0)\)
- \((−8,12)\)
- \((3,0)\)
- 回答
-
- 不
- 不
- 不
- 是的
- 是的
认识不等式解与其图之间的关系
在以下练习中,写下阴影区域所示的不等式。
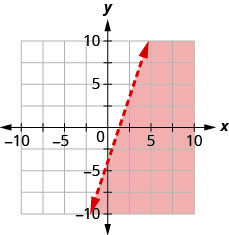
用边界线写下图表所示的不等式\(y=3x−4\)。
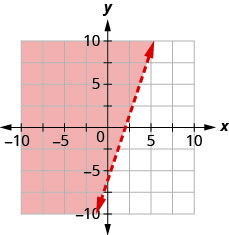
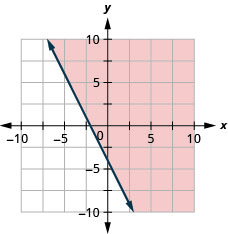
用边界线写下图表所示的不等式\(y=2x−4\)。
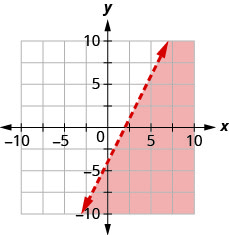
- 回答
-
\(y<2 x-4\)
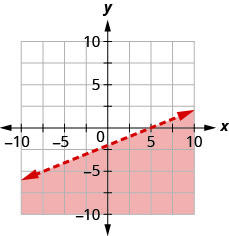
用边界线写下图表所示的不等式\(y=\frac{1}{2} x+1\)
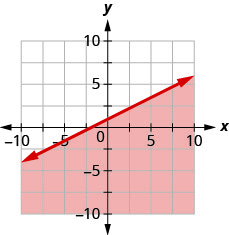
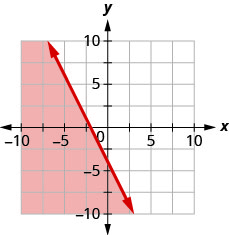
用边界线写下图表所示的不等式\(y=-\frac{1}{3} x-2\)
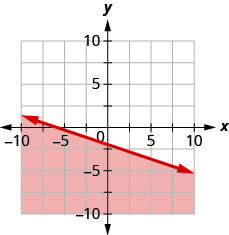
- 回答
-
\(y \leq-\frac{1}{3} x-2\)
用边界线写下图中阴影区域所示的不等式\(x+y=5\)。
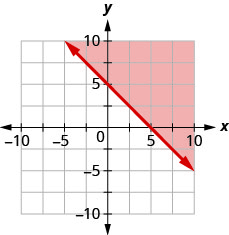
用边界线写下图中阴影区域所示的不等式\(x+y=3\)。
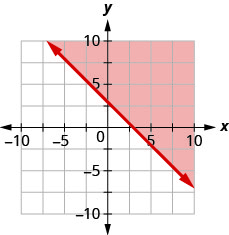
- 回答
-
\(x+y \geq 3\)
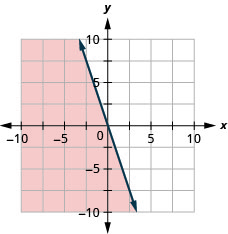
用边界线写下图中阴影区域所示的不等式\(2x+y=−4\)。
用边界线写下图中阴影区域所示的不等式\(x+2y=−2\)。
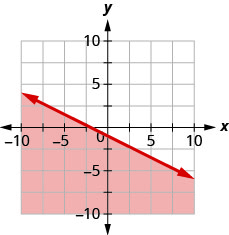
- 回答
-
\(x+2 y \geq-2\)
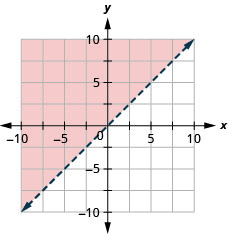
用边界线写下图中阴影区域所示的不等式\(3x−y=6\)。
用边界线写下图中阴影区域所示的不等式\(2x−y=4\)。
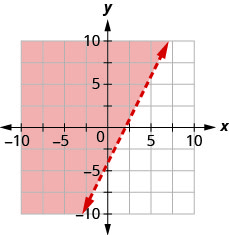
- 回答
-
\(2 x-y<4\)
用边界线写下图中阴影区域所示的不等式\(2x−5y=10\)。
用边界线写下图中阴影区域所示的不等式\(4x−3y=12\)。
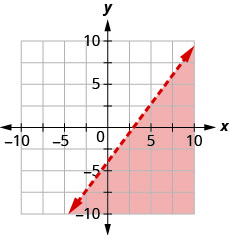
- 回答
-
\(4 x-3 y>12\)
绘制线性不等式
在以下练习中,绘制每个线性不等式的图表。
绘制线性不等式图\(y>\frac{2}{3} x-1\)
绘制线性不等式图\(y<\frac{3}{5} x+2\)
- 回答
-
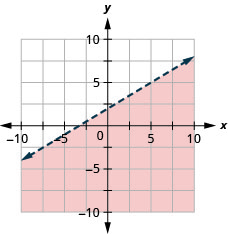
绘制线性不等式图\(y \leq-\frac{1}{2} x+4\)
绘制线性不等式图\(y \geq-\frac{1}{3} x-2\)
- 回答
-
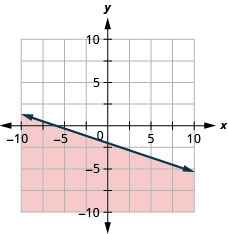
绘制线性不等式图\(x-y \leq 3\)
绘制线性不等式图\(x-y \geq -2\)
- 回答
-
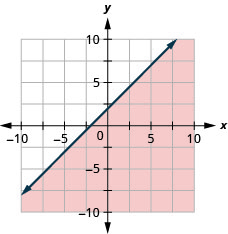
绘制线性不等式图\(4x+y>-4\)
绘制线性不等式图\(x+5y<-5\)
- 回答
-
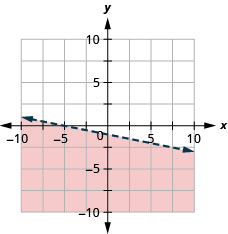
绘制线性不等式图\(3 x+2 y \geq-6\)
绘制线性不等式图\(4 x+2 y \geq-8\)
- 回答
-
绘制线性不等式图\(y>4x\)
绘制线性不等式图\(y>x\)
- 回答
-
绘制线性不等式图\(y \leq-x\)
绘制线性不等式图\(y \leq-3 x\)
- 回答
-
绘制线性不等式图\(y \geq-2\)
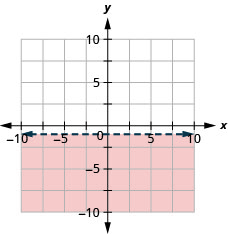
绘制线性不等式图\(y<-1\)
- 回答
-
绘制线性不等式图\(y<4\)
绘制线性不等式图\(y \geq 2\)
- 回答
-
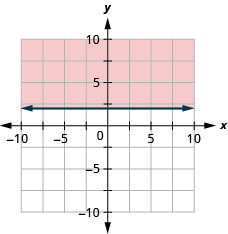
绘制线性不等式图\(x \leq 5\)
绘制线性不等式图\(x>-2\)
- 回答
-
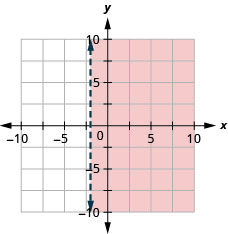
绘制线性不等式图\(x>-3\)
绘制线性不等式图\(x \leq 4\)
- 回答
-
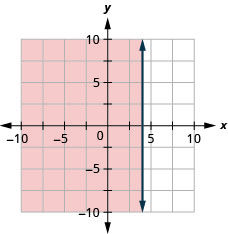
绘制线性不等式图\(x-y<4\)
绘制线性不等式图\(x-y<-3\)
- 回答
-
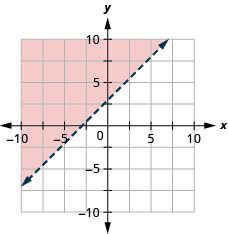
绘制线性不等式图\(y \geq \frac{3}{2} x\)
绘制线性不等式图\(y \leq \frac{5}{4} x\)
- 回答
-
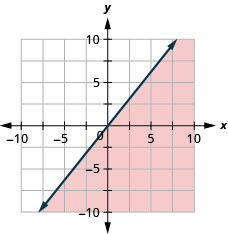
绘制线性不等式图\(y>-2 x+1\)
绘制线性不等式图\(y<-3 x-4\)
- 回答
-
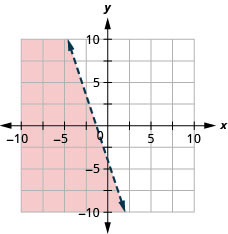
绘制线性不等式图\(x \leq-1\)
绘制线性不等式图\(x \geq 0\)
- 回答
-
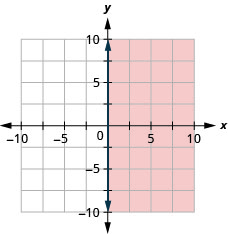
日常数学
钱。 Gerry 希望在教堂狂欢节开幕时在售票处获得最多 100 美元的现金。 他将有1美元的钞票和5美元的钞票。 如果\(x\)是1美元钞票的数量,\(y\)是5美元钞票的数量,则不等式\(x+5y \leq 100\)模拟了这种情况。
- 绘制不等式的图表。
- 列出不等式的三种解,\(x+5y \leq 100\)其中\(x\)和\(y\)都是整数。
购物。 图拉有20美元可以花在二手书销售上。 精装书每本售价2美元,平装书每本售价0.50美元。 如果说\(x\)是图拉可以买到的精装书的数量,以及她能买到的平装书的数量,那么不平等\(y\)就是这种情况的\(2x+\frac{1}{2} y \leq 20\)模范。
- 绘制不等式的图表。
- 列出不等式的三种解,\(2x+\frac{1}{2} y \leq 20\)其中\(x\)和\(y\)都是整数。
- 回答
-
1。
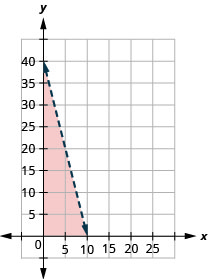
2。 答案会有所不同。
写作练习
莱斯特认为,任何带\(>\)符号的不平等的解决方案是线上方的区域,任何带\(<\)符号的不平等的解决方案是线下区域。 莱斯特对吗? 解释原因或原因。
解释为什么在某些线性不等式图中,边界线是实线,而在其他图中则是虚线。
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
b. 关于你对本部分的掌握程度,这份清单告诉了你什么? 你会采取哪些措施来改进?