4.7: 线性不等式图
- Page ID
- 204696
在本节结束时,您将能够:
- 验证两个变量中不等式的解
- 认识不等式解与其图之间的关系
- 绘制线性不等式
验证两个变量中不等式的解
我们已经学会了如何解决一个变量中的不等式。 现在,我们将研究两个变量中的不等式。 两个变量中的不等式有许多用途。 例如,如果你经营一家企业,你会希望你的收入大于成本,这样你的企业才能获利。
线性不等式是一种可以用以下形式之一书写的不等式:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]
其中\(A\)和不是\(B\)都为零。
你还记得一个变量的不等式有许多解吗? 不等式的解\(x>3\)是任何大于的数字\(3\)。 我们在数字行上显示了这一点,方法是在右边的数字行中加上阴影\(3\),然后在左括号处加上一个左括号\(3\)。 参见图\(\PageIndex{1}\)。

同样,两个变量中的不等式有很多解。 当我们在值中替换时\( (x, y)\),任何使不等式成真的有序对都是不等式的解。
当我们替换和的值时,如果不等式为真,则有序对\( (x, y)\)就是线性不\(x\)等式的解\(y\)。
确定每个有序对是否是不等式的解\(y>x+4\):
- \((0,0)\)
- \((1,6)\)
- \((2,6)\)
- \((−5,−15)\)
- \((−8,12)\)
- 回答
- 1。
2。\((0,0)\) 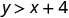

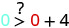
简化。 
所以,\((0,0)\)不是解决办法\(y>x+4\)。\((1,6)\) 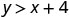

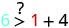
简化。 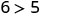
所以,\((1,6)\)是一个解决方案\(y>x+4\)。 - 3。
\((2,6)\) 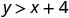


简化。 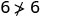
所以,\((2,6)\)不是解决办法\(y>x+4\)。 - 4。
\((−5,−15)\) 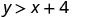
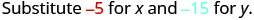
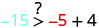
简化。 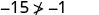
所以,\((−5,−15)\)不是解决办法\(y>x+4\)。 - 5。
(−8,12) 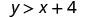

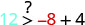
简化。 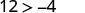
所以,\((−8,12)\)是一个解决方案\(y>x+4\)。
确定每个有序对是否是不等式的解\(y>x−3\):
- \((0,0)\)
- \((4,9)\)
- \((−2,1)\)
- \((−5,−3)\)
- \((5,1)\)
- 回答
-
- 是的
- 是的
- 是的
- 是的
- 不
确定每个有序对是否是不等式的解\(y<x+1\):
- \((0,0)\)
- \((8,6)\)
- \((−2,−1)\)
- \((3,4)\)
- \((−1,−4)\)
- 回答
-
- 是的
- 是的
- 不
- 不
- 是的
认识不等式解与其图之间的关系
现在,我们将研究不等式的解与其图表有何关系。
让我们\(\PageIndex{1}\)再想一想图中的数字线。 该点将该数字线\(x=3\)分为两部分。 一边\(3\)是所有数字都小于\(3\)。 另一方面,\(3\)所有数字都大于\(3\)。 参见图\(\PageIndex{2}\)。
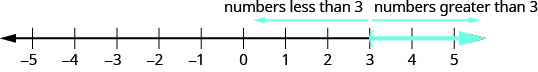
的解决方案\(x>3\)是右边数字线的阴影部分\(x=3\)。
同样,这条线将平面\(y=x+4\)分成两个区域。 直线的一侧是带有以下点的点\(y<x+4\)。 在这条线的另一边是带有的点\(y>x+4\)。 我们称这条线\(y=x+4\)为边界线。
带方程的直线\(Ax+By=C\)是分隔区域与所在\(Ax+By>C\)区域的边界线\(Ax+By<C\)。
对于一个变量中的不等式,端点用圆括号或方括号显示,具体取决于解中是否包含 aa:

同样,对于两个变量中的不等式,边界线以实线或虚线显示,以表示解中是否包含该直线。 表中对此进行了总结\(\PageIndex{1}\)。
| \(Ax+By<C\) | \(Ax+By\leq C\) |
| \(Ax+By>C\) | \(Ax+By\geq C\) |
| 解中不包括边界线。 | 边界线包含在解决方案中。 |
| 边界线为虚线。 | 边界线是实线。 |
现在,让我们来看看我们在练习中发现了什么\(\PageIndex{1}\)。 我们首先绘制线条\(y=x+4\),然后绘制我们测试的五个点。 参见图\(\PageIndex{3}\)。
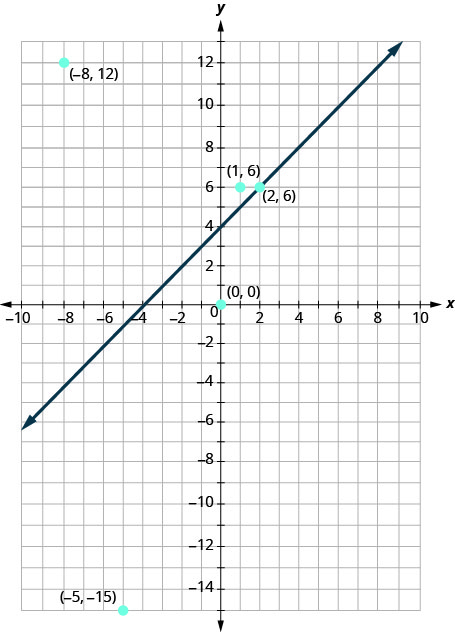
在练习中,\(\PageIndex{1}\)我们发现有些要点是解决不平等的办法\(y>x+4\),有些则不是。
我们绘制的哪个点是解决不平等的办法\(y>x+4\)? 要点\((1,6)\)和\((−8,12)\)是解决不平等的办法\(y>x+4\)。 请注意,它们都位于边界线的同一侧\(y=x+4\)。
这两个点\((0,0)\)和\((−5,−15)\)位于边界线的另一边\(y=x+4\),它们不是不等式的解\(y>x+4\)。 对于这两点,\(y<x+4\).
那重点\((2,6)\)呢? 因为\(6=2+4\),该点是方程的解\(y=x+4\)。 所以\((2,6)\)这个点在边界线上。
让我们在边界线的左侧再取一个点,测试它是否是不等式的解\(y>x+4\)。 该点\((0,10)\)显然在边界线的左边,不是吗? 这是解决不平等的办法吗?
\[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]
您在边界线左侧选择的任何点都是不等式的解\(y>x+4\)。 左边的所有点都是解决方案。
同样,边界线右侧的所有点(带\((0,0)\)和\((−5,−15)\)的一侧)都不是解\(y>x+4\)。 参见图\(\PageIndex{4}\)。
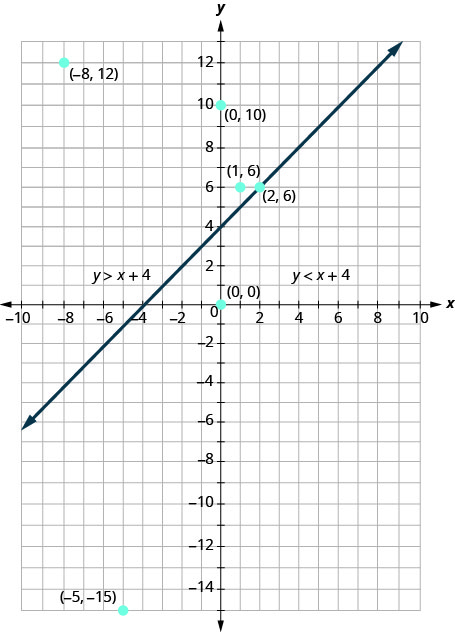
不等式图\(y>x+4\)如下图所\(\PageIndex{5}\)示。 这条线\(y=x+4\)将飞机分为两个区域。 阴影部分显示了不等式的解决方案\(y>x+4\)。
边界线上的点和位置\(y=x+4\)上的点不是不等式的解\(y>x+4\),因此线本身不是解的一部分。 我们通过将直线设为虚线,而不是实线来证明这一点。
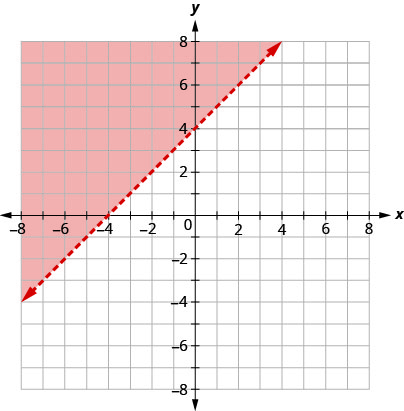
显示的边界线是\(y=2x−1\)。 写下图表所示的不等式。
- 回答
-
这条线\(y=2x−1\)是边界线。 直线的一侧是带有\(y>2x−1\)的点,另一侧是带点的点\(y<2x−1\)。
让我们测试一下这个点\((0,0)\),看看哪个不等式描述了它的边界线边。
在\((0,0)\),哪个不平等是正确的:
\[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]
既然\(y>2x−1\)是真的\((0,0)\),那就是解决方案。 阴影区域显示了不等式的解决方案\(y>2x−1\)。
由于边界线是用实线绘制的,因此不等式包括等号。
该图显示了不等式\(y\geq 2x−1\)。
我们可以使用任何点作为测试点,前提是它不在线上。 我们为什么选择\((0,0)\)? 因为它是最容易评估的。 你可能需要在边界线的另一边选取一个点然后检查一下\(y<2x−1\)。
用边界线写下图表所示的不等式\(y=−2x+3\)。
- 回答
-
\(y\geq −2x+3\)
用边界线写下图表所示的不等式\(y=\frac{1}{2}x−4\)。
- 回答
-
\(y \leq \frac{1}{2}x - 4\)
显示的边界线是\(2x+3y=6\)。 写下图表所示的不等式。
- 回答
-
这条线\(2x+3y=6\)是边界线。 直线的一侧是带有\(2x+3y>6\)的点,另一侧是带点的点\(2x+3y<6\)。
让我们测试一下这个点\((0,0)\),看看哪个不等式描述了它的边界线边。
在\((0,0)\),哪个不平等是正确的:
\[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]
所以,一边\((0,0)\)是哪一边\(2x+3y<6\)。
(你可能想在边界线的另一边选一个点然后检查一下\(2x+3y>6\)。)
由于边界线以虚线绘制,因此不等式不包含等号。
该图显示了不等式的解\(2x+3y<6\)。
用边界线写下图中阴影区域所示的不等式\(x−4y=8\)。
- 回答
-
\(x-4 y \leq 8\)
用边界线写下图中阴影区域所示的不等式\(3x−y=6\)。
- 回答
-
\(3 x-y \leq 6\)
绘制线性不等式
现在,我们已经准备好将所有这些放在一起,绘制线性不等式图。
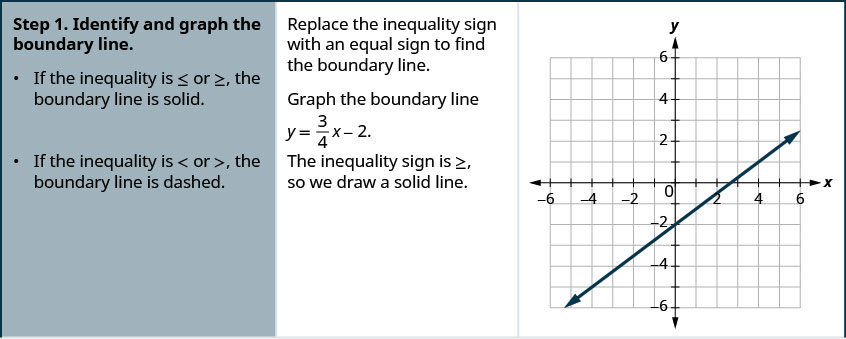
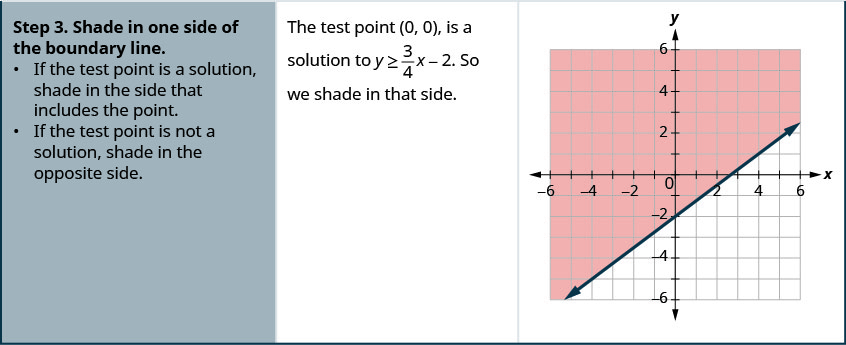
绘制线性不等式图\(y \geq \frac{3}{4} x-2\)。
- 回答
-

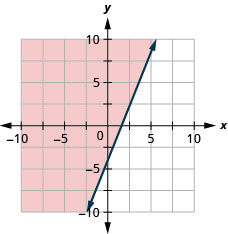
绘制线性不等式图\(y \geq \frac{5}{2} x-4\)。
- 回答
-
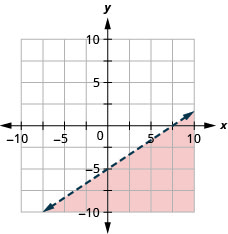
绘制线性不等式图\(y<\frac{2}{3} x-5\)。
- 回答
-
这里总结了我们绘制线性不等式图所采取的步骤。
- 识别边界线并绘制图表。
- 如果不等式为\(≤\)或\(≥\),则边界线为实线。
- 如果不等式为\(<\)或\(>\),则边界线为虚线。
- 测试不在边界线上的点。 这是不平等的解决方案吗?
- 边界线一侧的阴影。
- 如果测试点是解,则在包含该点的一侧加上阴影。
- 如果测试点不是解决方案,则在另一侧遮阳。
绘制线性不等式图\(x−2y<5\)。
- 回答
-
首先我们绘制边界线\(x−2y=5\)。 不平等\(<\)之处在于我们画一条虚线。
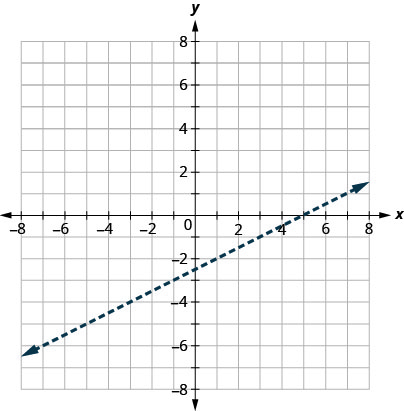
-
然后我们测试一个点。 我们将\((0,0)\)再次使用,因为它易于评估并且不在边界线上。
\((0,0)\)有解决方案\(x−2y<5\)吗?
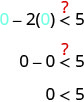
这个点\((0,0)\)是解\(x−2y<5\),所以我们在边界线的那一侧做阴影。
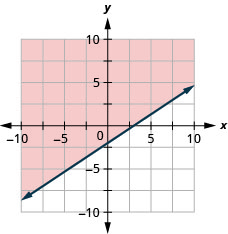
绘制线性不等式图\(2x−3y\leq 6\)。
- 回答
-
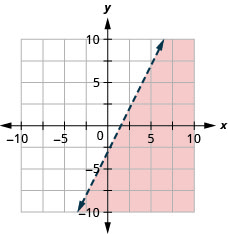
绘制线性不等式图\(2x−y>3\)。
- 回答
-
如果边界线穿过原点怎么办? 这样我们就不能\((0,0)\)用作测试点了。 没问题——我们只选择不在边界线上的其他点即可。
绘制线性不等式图\(y\leq −4x\)。
- 回答
-
首先我们绘制边界线\(y=−4x\)。 它采用斜率截距形式,带有 an\(m=−4\) d\(b=0\)。 不平等\(≤\)之处在于我们画一条实线。
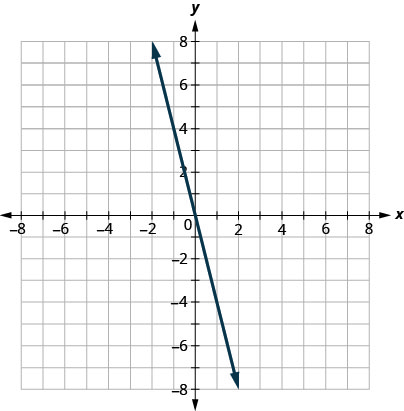
现在,我们需要一个测试点。 我们可以看到该点\((1,0)\)不在边界线上。
\((1,0)\)有解决方案\(y≤−4x\)吗?
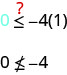
这个点\((1,0)\)不是解法\(y≤−4x\),所以我们在边界线的另一侧进行阴影。 参见图\(\PageIndex{6}\)。
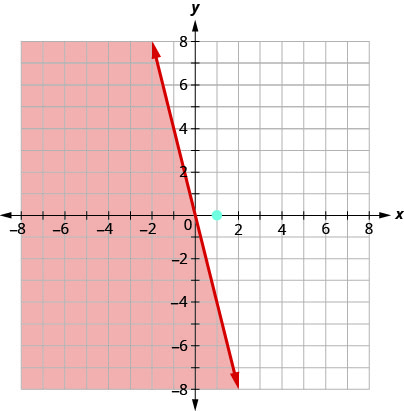
图\(\PageIndex{6}\)
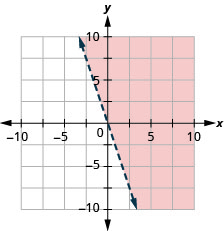
绘制线性不等式图\(y>−3x\)。
- 回答
-
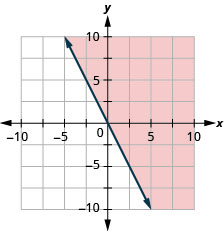
绘制线性不等式图\(y\geq −2x\)。
- 回答
-
一些线性不等式只有一个变量。 他们可能有 “\(x\)但没有\(y\)” 或 “a\(y\) 但没有”\(x\)。 在这些情况下,边界线要么是垂直线,要么是水平线。 你还记得吗?
\(\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}\)
绘制线性不等式图\(y>3\)。
- 回答
-
首先我们绘制边界线\(y=3\)。 它是一条水平线。 不平等\(>\)之处在于我们画一条虚线。
我们测试一下\((0,0)\)。
\[y>3 \\ 0\not>3\]
\((0,0)\)不是解决的办法\(y>3\)。
因此,我们会遮盖不包括的一面\((0,0)\)。
绘制线性不等式图\(y<5\)。
- 回答
-
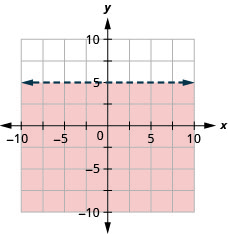
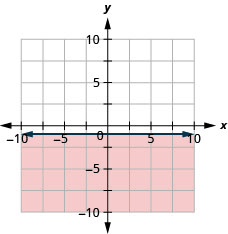
绘制线性不等式图\(y \leq-1\)。
- 回答
-
关键概念
- 绘制线性不等式图
- 识别边界线并绘制图表。
如果不等式为\(≤\)或\(≥\),则边界线为实线。
如果不等式为\(<\)或\(>\),则边界线为虚线。 - 测试不在边界线上的点。 这是不平等的解决方案吗?
- 边界线一侧的阴影。
如果测试点是解,则在包含该点的一侧加上阴影。
如果测试点不是解决方案,则在另一侧遮阳。
- 识别边界线并绘制图表。
词汇表
- 边界线
- 带有方程的直线\(A x+B y=C\),用于将区域与所在\(A x+B y>C\)区域分开\(A x+B y<C\)。
- 线性不等式
- 一种不等式,可以用以下形式之一书写:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]
其中\(B\),\(A\)和不是都为零。
- 线性不等式的解
- 有序对\((x,\,y)\)是线性不等式的解,当我们替换\(x\)和的值时,不等式是正确的\(y\)。


