第 4 章复习练习
- Page ID
- 204645
第 4 章复习练习
矩形坐标系
在矩形坐标系中绘制点
在以下练习中,在矩形坐标系中绘制每个点。
- (−1、−5)
- (−3,4)
- (2, −3)
- \(\left(1, \frac{5}{2}\right)\)
- (4,3)
- (−4,3)
- (−4、−3)
- (4, −3)
- 回答
-
- (−2,0)
- (0, −4)
- (0,5)
- (3,0)
- \(\left(2, \frac{3}{2}\right)\)
- \(\left(3, \frac{4}{3}\right)\)
- \(\left(\frac{1}{3},-4\right)\)
- \(\left(\frac{1}{2},-5\right)\)
- 回答
-
识别图表上的点
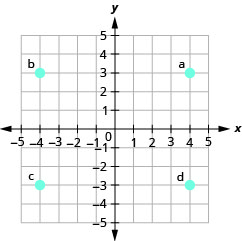
在以下练习中,命名矩形坐标系中显示的每个点的有序对。
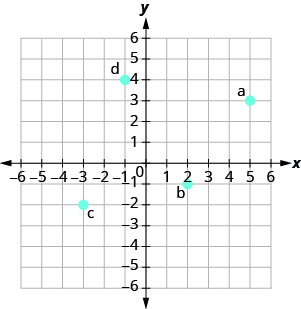
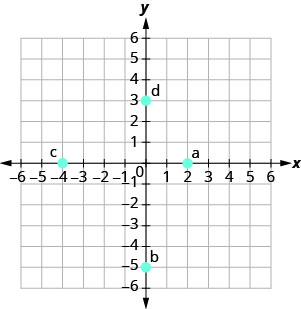
- 回答
-
a. (2,0)
b (0, −5)
c (−4.0)
d (0,3)
验证两个变量中方程的解
在以下练习中,哪些有序对是给定方程的解?
\(5x+y=10\)
- (5,1)
- (2,0)
- (4, −10)
\(y=6x−2\)
- (1,4)
- \(\left(\frac{1}{3}, 0\right)\)
- (6, −2)
- 回答
-
1、2
完成两个变量中线性方程的解表
在以下练习中,填写表格以找到每个线性方程的解。
\(y=4 x-1\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -2 |
\(y=-\frac{1}{2} x+3\)
| x | y | (x, y) |
| 0 | ||
| 4 | ||
| -2 |
- 回答
-
x y (x, y) 0 3 (0,3) 4 1 (4, 1) −2 4 (−2,4)
\(x+2 y=5\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -1 |
\(3x+2y=6\)
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -2 |
- 回答
-
x y (x, y) 0 −3 (0, −3) 2 0 (2,0) −2 −6 (−2、−6)
在两个变量中找到线性方程的解
在以下练习中,找到每个线性方程的三个解。
\(x+y=3\)
\(x+y=-4\)
- 回答
-
答案会有所不同。
\(y=3 x+1\)
\(y=-x-1\)
- 回答
-
答案会有所不同。
绘制线性方程图
认识方程解与其图之间的关系
在以下练习中,针对每个有序的对子决定:
- 有序对是方程的解吗?
- 点在直线上吗?
\(y=−x+4\)
(0,4) (−1,3)
(2,2) (−2,6)
\(y=\frac{2}{3} x-1\)
\((0,-1) (3,1)\)
\((-3,-3) (6,4)\)
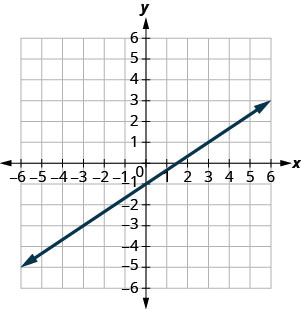
- 回答
-
- 是的;是的
- 是;不是
通过绘制点来绘制线性方程图
在以下练习中,通过绘制点来绘制图形。
\(y=4x-3\)
\(y=-3x\)
- 回答
-
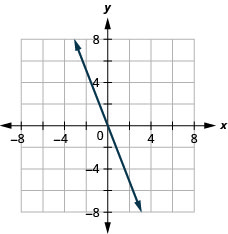
\(y=\frac{1}{2} x+3\)
\(x-y=6\)
- 回答
-
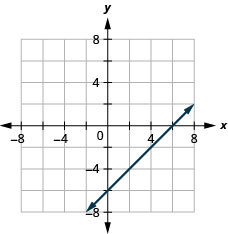
\(2x+y=7\)
\(3x-2y=6\)
- 回答
-
绘制垂直线和水平线
在以下练习中,绘制每个方程的图表。
\(y=-2\)
\(x=3\)
- 回答
-
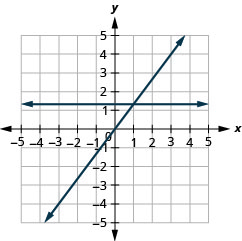
在以下练习中,用相同的矩形坐标系绘制每对方程的图形。
\(y=-2 x\)和\(y=-2\)
\(y=\frac{4}{3} x\)和\(y=\frac{4}{3}\)
- 回答
-
使用截图绘制图表
识别图表上的\(x\)\(y\)-和-截取
在以下练习中,找到\(x\)-和\(y\)-截取。
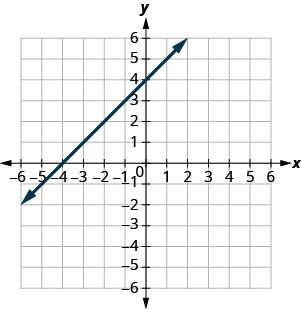
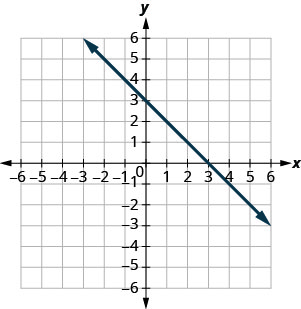
- 回答
-
\((3,0)\)和\((0,3)\)
从直线方程中找\(y\)出\(x\)-和-截距
在以下练习中,找到每个方程的截距。
\(x+y=5\)
\(x-y=-1\)
- 回答
-
\((-1,0),(0,1)\)
\(x+2y=6\)
\(2x+3y=12\)
- 回答
-
\((6,0),(0,4)\)
\(y=\frac{3}{4} x-12\)
\(y=3x\)
- 回答
-
\((0,0)\)
使用截图画一条线
在以下练习中,使用截获量绘制图表。
\(-x+3y=3\)
\(x+y=-2\)
- 回答
-
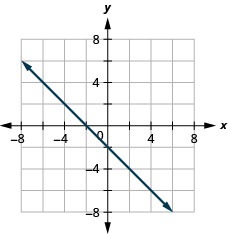
\(x-y=4\)
\(2x-y=5\)
- 回答
-
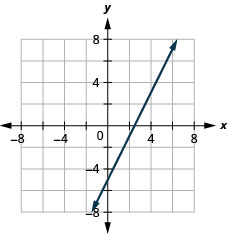
\(2x-4y=8\)
\(y=2x\)
- 回答
-
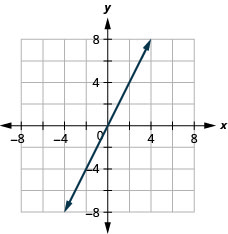
直线的斜率
使用地理板对坡度进行建模
在以下练习中,找到在每个地理板上建模的斜率。
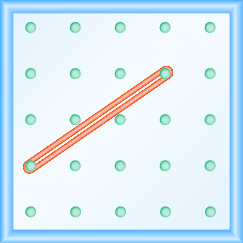
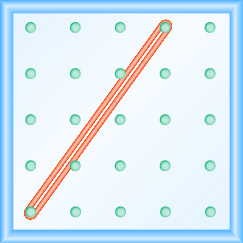
- 回答
-
\(\frac{4}{3}\)
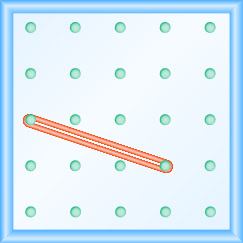
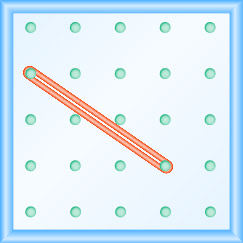
- 回答
-
\(-\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{3}{2}\)
- 回答
-
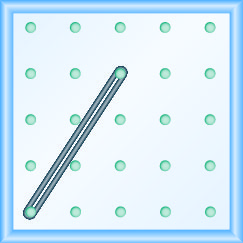
\(-\frac{2}{3}\)
\(-\frac{1}{2}\)
- 回答
-
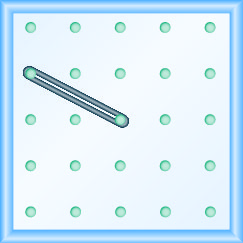
\(m=\frac{\text { rise }}{\text { run }}\)用于从曲线图中找出直线的斜率
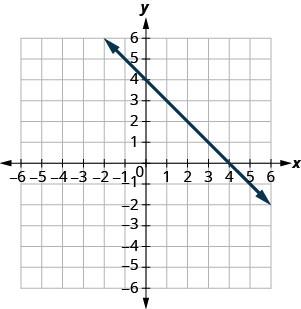
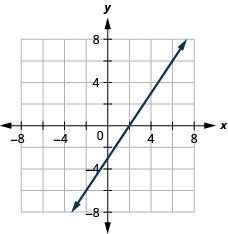
在以下练习中,找到所示每条线的斜率。
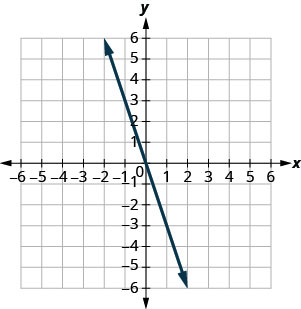
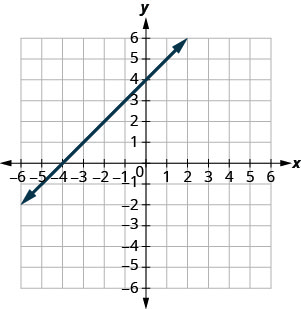
- 回答
-
1
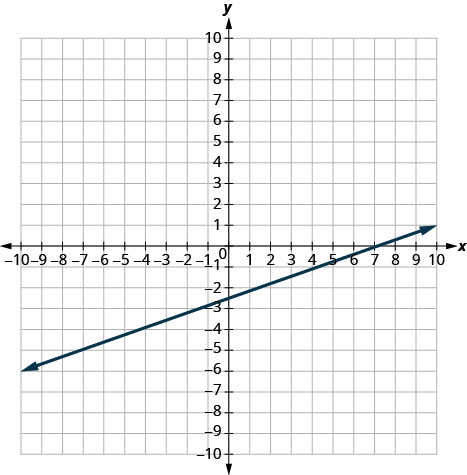
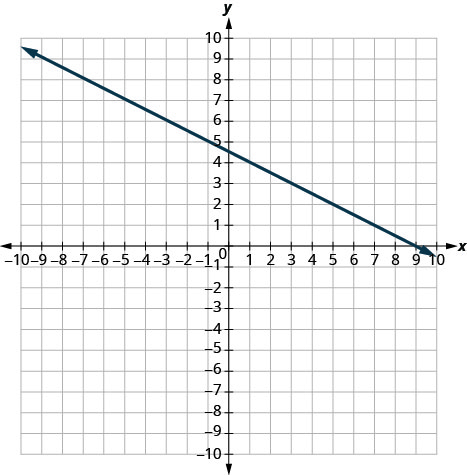
- 回答
-
\(-\frac{1}{2}\)
找出水平线和垂直线的斜率
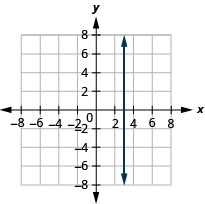
在以下练习中,找出每条线的斜率。
\(y=2\)
\(x=5\)
- 回答
-
未定义
\(x=-3\)
\(y=-1\)
- 回答
-
0
使用斜率公式求出两点间直线的斜率
在以下练习中,使用斜率公式求出每对点之间的直线的斜率。
\((-1,-1),(0,5)\)
\((3,5),(4,-1)\)
- 回答
-
−6
\((-5,-2),(3,2)\)
\((2,1),(4,6)\)
- 回答
-
\(\frac{5}{2}\)
给定一个点和斜率绘制一条直线
在以下练习中,用给定的点和斜率绘制每条线。
\((2,-2) ; \quad m=\frac{5}{2}\)
\((-3,4) ; \quad m=-\frac{1}{3}\)
- 回答
-
\(x\)-截距\(-4 ; \quad m=3\)
\(y\)-截距\(1 ; \quad m=-\frac{3}{4}\)
- 回答
-
求解斜率应用程序
在以下练习中,求解这些斜率应用程序。
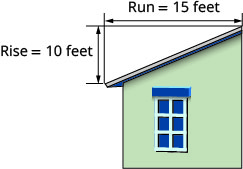
下图所示的屋顶有一\(10\)英尺的上升和一英\(15\)尺的长度。 它的斜率是多少?
山路上升一\(500\)英\(50\)尺. 它的斜率是多少?
- 回答
-
\(\frac{1}{10}\)
直线方程的截距形式
识别图形与直线方程的斜率截距形式之间的关系
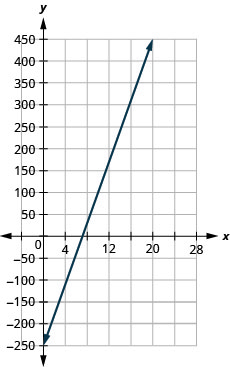
在以下练习中,使用图表找出每条线的斜率和 y 截距。 将这些值与方程进行比较\(y=mx+b\)。
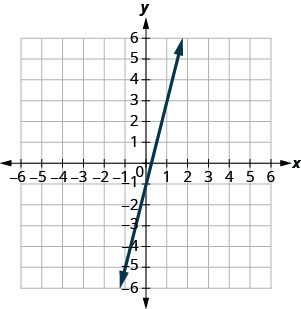
\(y=4x−1\)
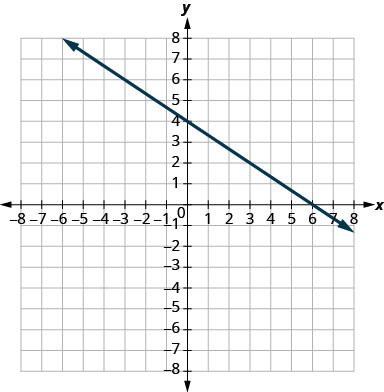
\(y=-\frac{2}{3} x+4\)
- 回答
-
斜\(y\)率\(m=-\frac{2}{3}\)和截距\((0,4)\)
从直线方程中识别斜率和 Y 截距
在以下练习中,确定每条线的斜率和\(y\)截距。
\(y=-4 x+9\)
\(y=\frac{5}{3} x-6\)
- 回答
-
\(\frac{5}{3} ;(0,-6)\)
\(5x+y=10\)
\(4x-5y=8\)
- 回答
-
\(\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)\)
使用斜率和截距绘制直线图
在以下练习中,使用斜率和\(y\)截距绘制每个方程的直线。
\(y=2x+3\)
\(y=-x-1\)
- 回答
-
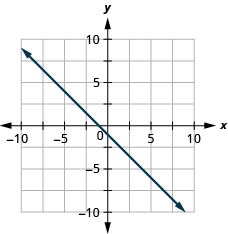
\(y=-\frac{2}{5} x+3\)
\(4x-3y=12\)
- 回答
-
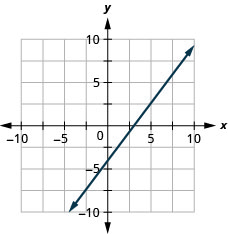
在以下练习中,确定绘制每条线的最便捷方法。
\(x=5\)
\(y=-3\)
- 回答
-
水平线
\(2x+y=5\)
\(x-y=2\)
- 回答
-
截住
\(y=x+2\)
\(y=\frac{3}{4} x-1\)
- 回答
-
绘制点
绘制和解释坡度截距的应用
凯瑟琳是一名私人厨师。 该方程\(C=6.5m+42\)模拟了她每周的费用(以美元计)与她供应的膳食数量之间的关系。\(C\)\(m\)
- 找出凯瑟琳不吃饭一周的费用。
- 找出她一周提供\(14\)膳食的费用。
- 解释方程的斜率和\(C\)截距。
- 绘制方程图。
玛乔丽教钢琴。 该方程式\(P=35h−250\)模拟了她以美元计算的每周利润与她所教的学生课程数量之间的关系。\(P\)\(s\)
- 查看 Marjorie 一周不教学生课时的利润。
- 当她教\(20\)学生课时,可以找到一周的利润。
- 解释方程的斜率和\(P\)截距。
- 绘制方程图。
- 回答
-
- \(−$250\)
- \($450\)
- 斜率意味\(35\)着 Marjorie 每多教一次学生\(P\),她的每周利润就会增加。\($35\) \(P\)-intercept 表示当课程数量达到时\(0\),Marjorie 输了\($250\)。
使用斜率识别平行线
在以下练习中,使用斜率和\(y\)-intercepts来确定线是否平行。
\(4x-3y=-1 ; \quad y=\frac{4}{3} x-3\)
\(2 x-y=8 ; \quad x-2 y=4\)
- 回答
-
不平行
使用斜率识别垂直线
在以下练习中,使用斜率和 y 截距来确定直线是否垂直。
\(y=5x-1 ; \quad 10x+2y=0\)
\(3x-2y=5 ; \quad 2x+3y=6\)
- 回答
-
垂直
求直线方程
给定斜率和 y 截距求直线方程
在以下练习中,找到具有给定斜率和\(y\)截距的直线的方程。 以斜率截距形式写下方程。
斜\(y\)率\(\frac{1}{3}\)和截距\((0,-6)\)
斜\(y\)率\(-5\)和截距\((0,-3)\)
- 回答
-
\(y=-5x-3\)
斜\(y\)率\(0\)和截距\((0,4)\)
斜\(y\)率\(-2\)和截距\((0,0)\)
- 回答
-
\(y=-2x\)
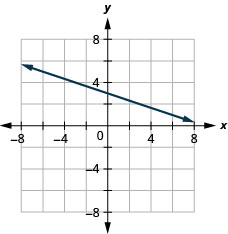
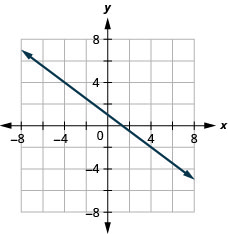
在以下练习中,找到每张图中显示的直线的方程。 以斜率截距形式写下方程。
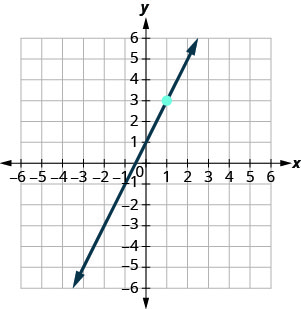
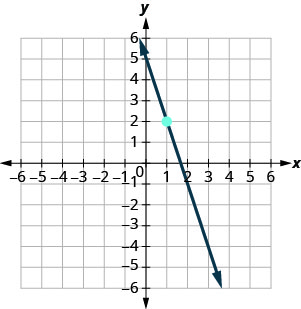
- 回答
-
\(y=-3x+5\)
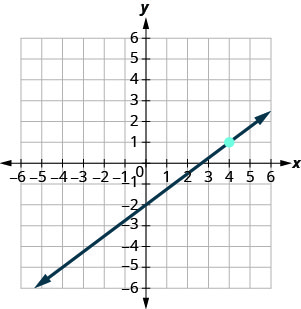
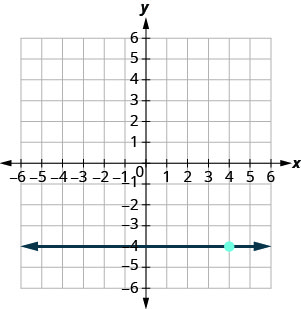
- 回答
-
\(y=-4\)
在给定斜率和点的情况下求直线方程
在以下练习中,找到具有给定斜率并包含给定点的直线的方程。 以斜率截距形式写下方程。
\(m=-\frac{1}{4},\)点\((-8,3)\)
\(m=\frac{3}{5},\)点\((10,6)\)
- 回答
-
\(y=\frac{3}{5} x\)
水平线包含\((-2,7)\)
\(m=-2,\)点\((-1,-3)\)
- 回答
-
\(y=-2x-5\)
给定两点求直线方程
在以下练习中,找到包含给定点的直线的方程。 以斜率截距形式写下方程。
\((2,10)\)和\((-2,-2)\)
\((7,1)\)和\((5,0)\)
- 回答
-
\(y=\frac{1}{2} x-\frac{5}{2}\)
\((3,8)\)和\((3,-4)\)
\((5,2)\)和\((-1,2)\)
- 回答
-
\(y=2\)
求一条平行于给定直线的直线的方程
在以下练习中,找到一条平行于给定直线且包含给定点的直线的方程。 以斜率截距形式写下方程。
线\(y=-3x+6,\)点\((1,-5)\)
线\(2x+5y=-10,\)点\((10,4)\)
- 回答
-
\(y=-\frac{2}{5} x+8\)
线\(x=4,\)点\((-2,-1)\)
线\(y=-5,\)点\((-4,3)\)
- 回答
-
\(y=3\)
求一条垂直于给定直线的直线的方程
在以下练习中,找到一条垂直于给定直线并包含给定点的直线的方程。 以斜率截距形式写下方程。
线\(y=-\frac{4}{5} x+2,\)点\((8,9)\)
线\(2x-3y=9,\)点\((-4,0)\)
- 回答
-
\(y=-\frac{3}{2} x-6\)
线\(y=3,\)点\((-1,-3)\)
线\(x=-5\)点\((2,1)\)
- 回答
-
\(y=1\)
绘制线性不等式
验证两个变量中不等式的解
在以下练习中,确定每个有序对是否是给定不等式的解。
确定每个有序对是否是不等式的解\(y<x−3\):
- \((0,1)\)
- \((−2,−4)\)
- \((5,2)\)
- \((3,−1)\)
- \((−1,−5)\)
确定每个有序对是否是不等式的解\(x+y>4\):
- \((6,1)\)
- \((−3,6)\)
- \((3,2)\)
- \((−5,10)\)
- \((0,0)\)
- 回答
-
- 是的
- 不
- 是的
- 是的
- 不
认识不等式解与其图之间的关系
在以下练习中,写下阴影区域所示的不等式。
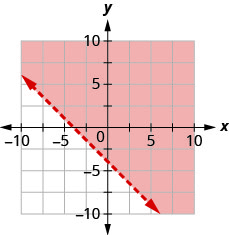
用边界线写下图表所示的不等式\(y=−x+2\)。
用边界线写下图表所示的不等式\(y=\frac{2}{3} x-3\)
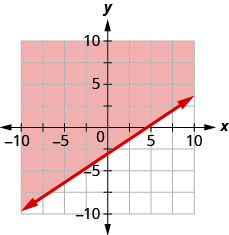
- 回答
-
\(y>\frac{2}{3} x-3\)
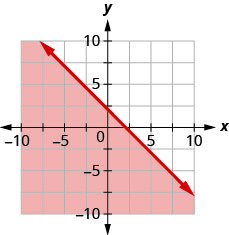
用边界线写下图中阴影区域所示的不等式\(x+y=−4\)。
用边界线写下图中阴影区域所示的不等式\(x−2y=6\)。
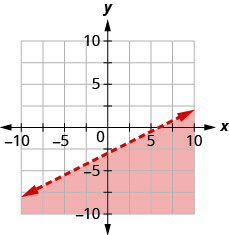
- 回答
-
\(x-2 y \geq 6\)
绘制线性不等式
在以下练习中,绘制每个线性不等式的图表。
绘制线性不等式图\(y>\frac{2}{5} x-4\)
绘制线性不等式图\(y \leq-\frac{1}{4} x+3\)
- 回答
-
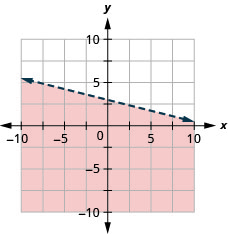
绘制线性不等式图\(x-y \leq 5\)
绘制线性不等式图\(3 x+2 y>10\)
- 回答
-
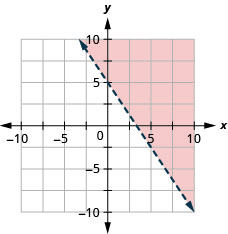
绘制线性不等式图\(y \leq-3 x\)
绘制线性不等式图\(y<6\)
- 回答
-
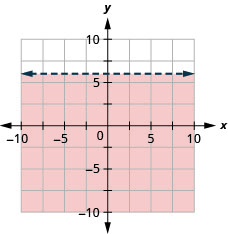
练习测试
在矩形坐标系中绘制每个点。
- \((2,5)\)
- \((−1,−3)\)
- \((0,2)\)
- \(\left(-4, \frac{3}{2}\right)\)
- \((5,0)\)
给定的有序对中哪些是方程的解\(3x−y=6\)?
- \((3,3)\)
- \((2,0)\)
- \((4,−6)\)
- 回答
-
- 是的
- 是的
- 不
找到线性方程的三个解\(y=-2x-4\)
找出方程的\(x\)-和\(y\)-截距\(4x-3y=12\)
- 回答
-
\((3,0),(0,-4)\)
找到所示每条线的斜率。
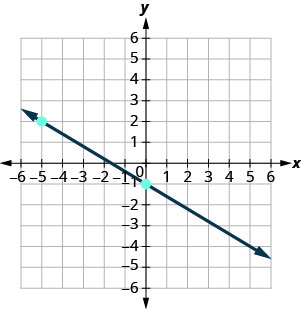
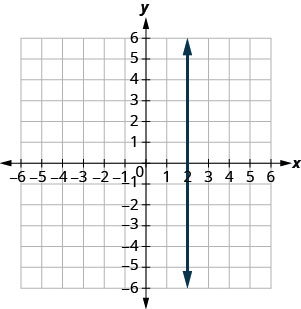
- 回答
-
未定义
找出两点\((5,2)\)和两点之间的直线的斜率\((-1,-4)\)
- 回答
-
1
用\(\frac{1}{2}\)包含点的斜率绘制直线图\((-3,-4)\)
绘制以下每个方程的直线。
\(y=\frac{5}{3} x-1\)
- 回答
-
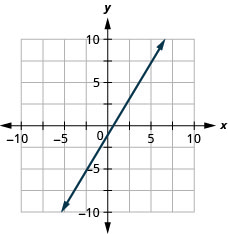
\(y=-x\)
\(x-y=2\)
- 回答
-
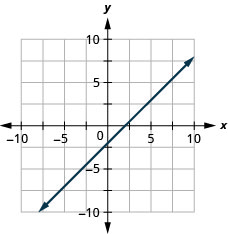
\(4x+2y=-8\)
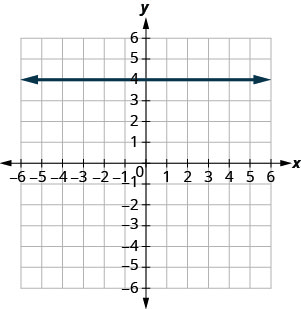
\(y=2\)
- 回答
-
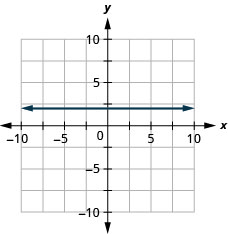
\(x=-3\)
找出每条线的方程。 以斜率截距形式写下方程。
斜\(y\)率\(-\frac{3}{4}\)和截距\((0,-2)\)
- 回答
-
\(y=-\frac{3}{4} x-2\)
\(m=2,\)点\((-3,-1)\)
包含\((10,1)\)和\((6,-1)\)
- 回答
-
\(y=\frac{1}{2} x-4\)
平行于\(y=-\frac{2}{3} x-1,\)包含该点的直线\((-3,8)\)
垂直于\(y=\frac{5}{4} x+2,\)包含该点的直线\((-10,3)\)
- 回答
-
\(y=-\frac{4}{5} x-5\)
用边界线写下图表所示的不等式\(y=−x−3\)。
绘制每个线性不等式的图像。
\(y>\frac{3}{2} x+5\)
- 回答
-
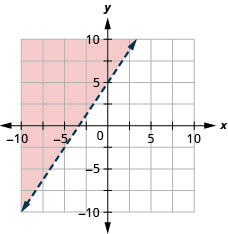
\(x-y \geq-4\)
\(y \leq-5 x\)
- 回答
-
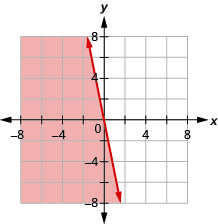
\(y<3\)