4.6: 求直线方程
- Page ID
- 204644
在本节结束时,您将能够:
- 给定斜率和 y 截距,求直线方程
- 在给定斜率和点的情况下找出直线的方程
- 在给定两点的情况下找出直线的方程
- 求一条平行于给定直线的直线的方程
- 求一条垂直于给定直线的直线的方程
在开始之前,请参加这个准备测验。
- 解决:\(\frac{2}{3} = \frac{x}{5}\)。
如果您错过了此问题,请查看练习 2.2.4。 - 简化:\(−\frac{2}{5}(x−15)\)。
如果您错过了此问题,请查看练习 1.10.34。
在线零售商如何根据你刚刚订购的商品知道 “你可能也会喜欢” 一件特定的商品? 经济学家怎么知道最低工资的提高将如何影响失业率? 医学研究人员如何创造靶向癌细胞的药物? 交通工程师如何预测汽油价格上涨或下降对通勤时间的影响? 都是数学。
你正处于数学之旅中一个激动人心的时刻,因为你正在学习的数学在现实世界中有有趣的应用。
物理科学、社会科学和商业世界充满了可以用关联两个变量的线性方程进行建模的情境。 收集数据并绘制图表。 如果数据点看起来形成一条直线,则可以使用该直线的方程根据另一个变量的值来预测一个变量的值。
要创建两个变量之间线性关系的数学模型,我们必须能够找到直线的方程。 在本节中,我们将介绍几种写直线方程的方法。 我们使用的具体方法将取决于我们获得的信息。
给定斜率和 y 截距求直线方程
如果方程以 slope—intercept 形式书写,y=mx+b,我们可以很容易地确定直线的斜率和截距。现在,我们将反过来——我们将从斜率和 y 截距开始,然后用它们来求直线的方程。
找出斜率为 −7 和 y 截距 (0, −1) 的直线的方程。
- 回答
-
由于我们得到了直线的斜率和 y 截距,因此我们可以将所需的值替换为 slope—intercept 形式,即 y=mx+b。
命名斜坡。 
命名为 y 截距。 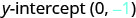
将这些值替换为 y=mx+b。 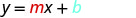
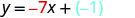
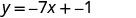
找出具有斜率\(\frac{2}{5}\)和 y 截距 (0,4) 的直线的方程。
- 回答
-
\(y = \frac{2}{5}x + 4\)
找出斜率为 −1 和 y 截距 (0, −3) 的直线的方程。
- 回答
-
\(y=−x−3\)
有时,需要根据图表确定斜率和截距。
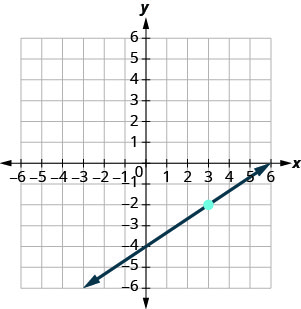
找到所示直线的方程。
- 回答
-
我们需要从图中找到直线的斜率和 y 截距,这样我们就可以将所需的值替换为 slope—intercept 形式 y=mx+by=mx+b。
为了找到斜率,我们在图表上选择两个点。
y 截距为 (0, −4),图形通过 (3, −2)。
通过计算上升和跑步来找到斜率。 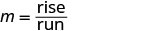

找出 y 截距。 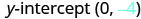
将这些值替换为 y=mx+b。 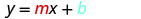
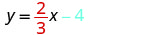
找到图中显示的直线的方程。
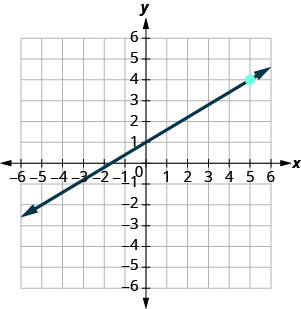
- 回答
-
\(y=\frac{3}{5}x+1\)
找到图中显示的直线的方程。
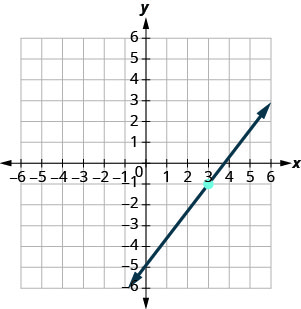
- 回答
-
\(y=\frac{4}{3}x−5\)
在给定斜率和点的情况下求直线方程
当你得到斜率和 y 截距或者从图表中读取它们时,使用方程的坡度-截距形式找到直线方程效果很好。 但是当你有另一个点而不是 y 截距时会发生什么?
我们将使用斜率公式推导出另一种形式的直线方程。 假设我们有一条斜率为 mm 的直线,它包含一些特定的点\((x_{1}, y_{1})\)和另一个点,我们称之为 (x, y)。 我们可以写出这条线的斜率,然后将其更改为不同的形式。
\(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)
这种格式称为直线方程的点斜率形式。
斜率为 mm 且包含点的直线方程的点-斜率形式\((x_{1}, y_{1})\)为
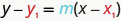
当给定斜率和一个点时,我们可以使用方程的点-斜率形式来找出直线的方程。 然后,我们将以斜率截距形式重写方程。 线性方程的大多数应用都使用斜率截距形式。
找出一条斜率\(m=\frac{2}{5}\)包含点 (10,3) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-




找出具有斜率\(m=\frac{5}{6}\)且包含点 (6,3) 的直线的方程。
- 回答
-
\(y=\frac{5}{6}x−2\)
求具有斜率\(m=\frac{2}{3}\)且包含点 (9,2) 的直线的方程。
- 回答
-
\(y=\frac{2}{3}x−4\)
- 确定斜率。
- 找出重点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写下方程。
找出一条斜率\(m=−\frac{1}{3}\)包含点 (6, −4) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-
既然我们得到了一个点和直线的斜率,我们可以将所需的值替换为 point—slope 形式\(y−y_{1}=m(x−x_{1})\)。
确定斜率。 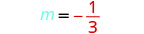
找出重点。 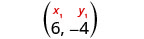
将这些值替换为\(y−y_{1}=m(x−x_{1})\)。 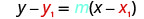
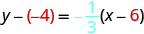
简化。 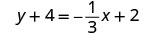
以斜率截距形式书写。 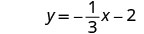
求具有斜率\(m=−\frac{2}{5}\)且包含点 (10, −5) 的直线的方程。
- 回答
-
\(y=−\frac{2}{5}x−1\)
找出带有斜率且包含点 (4\(m=−\frac{3}{4}\), −7) 的直线的方程。
- 回答
-
\(y=−\frac{3}{4}x−4\)
找到包含点 (−1,2) 的水平线方程。 以斜率截距形式写下方程。
- 回答
-
每条水平线的斜率为 0。 我们可以将斜率和点替换为 point—slope 形式,\(y−y_{1}=m(x−x_{1})\)。
我们最终得到了一条水平线的形式吗,y=a?确定斜率。 
找出重点。 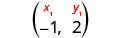
将这些值替换为\(y−y_{1}=m(x−x_{1})\)。 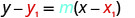
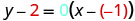
简化。 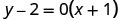
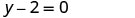
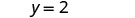
以斜率截距形式书写。 它采用 y 格式,但可以写成 y=0x+2。
找到包含点 (−3,8) 的水平线的方程。
- 回答
-
y = 8
找到包含点 (−1,4) 的水平线的方程。
- 回答
-
y = 4
在给定两点的情况下求直线方程
收集真实数据时,可以从两个数据点创建线性模型。 在下一个例子中,我们将看到在只给出两个点的情况下如何找到一条直线的方程。
到目前为止,我们有两种方法可以找到直线方程:斜率—截距或点—斜率。 因为我们会知道两个点,所以使用 point—slope 形式会更有意义。
但是接下来我们需要斜坡。 我们能找到只有两个点的斜坡吗? 是的。 然后,一旦我们有了斜率,我们就可以使用它和给定点之一来找到方程式。
找到包含点 (5,4) 和 (3,6) 的直线方程。 以斜率截距形式写下方程。
- 回答
-




使用点 (3,6),看看你得到的是相同的方程式。
找到包含点 (3,1) 和 (5,6) 的直线的方程。
- 回答
-
\(y=\frac{5}{2}x−\frac{13}{2}\)
找到包含点 (1,4) 和 (6,2) 的直线的方程。
- 回答
-
\(y=−\frac{2}{5}x+\frac{22}{5}\)
- 使用给定的点找出斜率。
- 选择一个点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写下方程。
找一个包含点 (−3, −1) 和 (2, −2) 的直线方程。 以斜率截距形式写下方程。
- 回答
-
由于我们有两个点,我们将使用点-斜率形式找到直线方程。 第一步将是找到斜坡。
找出直线通过 (−3, −1) 和 (2, −2) 的斜率。 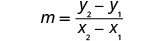
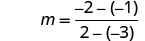
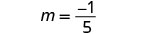
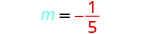
选择任一点。 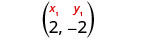
将这些值替换为\(y−y_{1}=m(x−x_{1})\)。 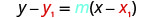
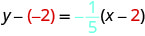
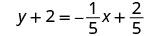
以斜率截距形式书写。 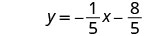
找到包含点 (−2, −4) 和 (1, −3) 的直线的方程。
- 回答
-
\(y=\frac{1}{3}x−\frac{10}{3}\)
找到包含点 (−4, −3) 和 (1, −5) 的直线的方程。
- 回答
-
\(y=−\frac{2}{5}x−\frac{23}{5}\)
找一个包含点 (−2,4) 和 (−2, −3) 的直线方程。 以斜率截距形式写下方程。
- 回答
-
同样,第一步将是找到斜坡。
\(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)
这告诉我们这是一条垂直线。 我们两个点的 x 坐标均为 −2。 因此,我们的直线方程为 x=−2。 既然没有 yy,我们就不能用斜率截距的形式写出来。
您可能需要使用两个给定的点绘制图表。 该图是否符合我们的结论,即这是一条垂直线?
找到包含点 (5,1) 和 (5, −4) 的直线的方程。
- 回答
-
x = 5
找到包含点 (−4,4) 和 (−4,3) 的直线的方程。
- 回答
-
x=−4
我们已经看到,我们可以使用斜率-截距形式或点-斜率形式来找到直线的方程。 我们使用哪种形式将取决于我们获得的信息。 表中对此进行了总结\(\PageIndex{1}\)。
| 写出直线方程 | ||
| 如果给出: | 使用: | 表格: |
| 斜率和 y 截距 | 斜率—截距 | y=mx+b |
| 斜率和点 | 点—斜率 | \(y−y_{1}=m(x−x_{1})\) |
| 两点积分 | 点—斜率 | \(y−y_{1}=m(x−x_{1})\) |
求一条平行于给定直线的直线的方程
假设我们需要找到一条穿过特定点且平行于给定直线的直线的方程。 我们可以利用平行线具有相同斜率的事实。 因此,我们将得到一个点和斜率——这正是我们使用点斜率方程所需要的。
首先让我们用图形来看一下。
该图显示了 y=2x−3 的图形。 我们想绘制一条平行于这条线并穿过该点 (−2,1) 的直线。
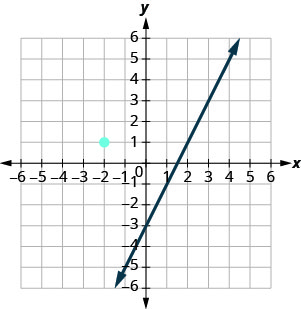
我们知道平行线的斜率相同。 因此,第二条线的斜率将与 y=2x−3 相同。 那个斜坡是\(m_{\|} = 2\)。 我们将使用符号\(m_{\|}\)来表示与斜率为 m 的直线平行的直线的斜率。(请注意,下标看起来像两条平行线。)
第二行将通过 (−2,1) 并有 m=2。 为了绘制直线图,我们从 (−2,1) 开始,然后计算上升并运行。 使用 m=2(或\(m=\frac{2}{1}\)),我们计算上升 2 和运行 1。 我们划清界限。
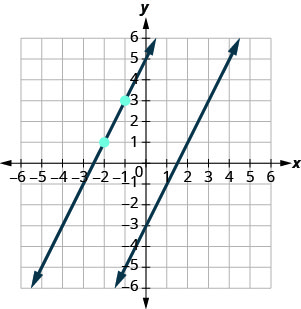
线条看起来平行吗? 第二行会通过 (−2,1) 吗?
现在,让我们看看如何用代数来做到这一点。
我们可以使用斜率截距形式或点-斜率形式来求直线方程。 在这里,我们知道一个点,就可以找到斜率。 因此,我们将使用点-斜率形式。
找一个平行于 y=2x−3 且包含点 (−2,1) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-
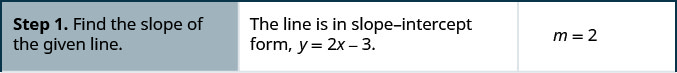




这个方程有意义吗? 这条线的 y 截距是多少? 斜率是多少?
找到一条平行于包含点 (4,2) 的直线 y=3x+1 的方程。 以斜率截距形式写下方程。
- 回答
-
y=3x−10
找到一条平行于包含点 (6,4) 的直线\(y=\frac{1}{2}x−3\)的方程。
- 回答
-
\(y=\frac{1}{2}x+1\)
- 找出给定直线的斜率。
- 找出平行线的斜率。
- 找出重点。
- 将这些值替换为 point—slope 形式,\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写下方程。
求一条垂直于给定直线的直线的方程
现在,让我们考虑垂直线。 假设我们需要找到一条穿过特定点且垂直于给定直线的直线。 我们可以利用这样一个事实,即垂直线的斜率为负倒数。 我们将再次使用点斜率方程,就像我们对平行线所做的那样。
该图显示了 y=2x−3 的图形。 现在,我们要绘制一条垂直于这条直线并穿过的直线 (−2,1)。

我们知道垂直线的斜率是负倒数。 我们将使用符号\(m_{\perp}\)来表示垂直于斜率为 m 的直线的斜率(请注意,下标\(_{\perp}\)看起来像两条垂直线形成的直角。)
\[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]
我们现在知道垂直线将通过 (−2,1)\(m_{\perp}=−\frac{1}{2}\)。
要绘制直线图,我们将从 (−2,1) 开始,然后计算上升 −1 和游程 2。 然后我们画出界限。
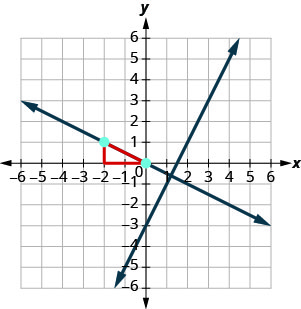
线条看起来是垂直的吗? 第二行会通过 (−2,1) 吗?
现在,让我们看看如何用代数来做到这一点。 我们可以使用斜率截距形式或点-斜率形式来求直线方程。 在这个例子中,我们知道一个点,并且可以找到斜率,所以我们将使用点-斜率形式。
找到一条垂直于 y=2x−3 且包含点 (−2,1) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-





找到一条垂直于包含点 (4,2) 的直线 y=3x+1 的方程。 以斜率截距形式写下方程。
- 回答
-
\(y=−\frac{1}{3}x+\frac{10}{3}\)
找出与包含点的直线\(y=\frac{1}{2}x−3\)垂直的方程 (6,4)。
- 回答
-
y=−2x+16
- 找出给定直线的斜率。
- 找出垂直线的斜率。
- 找出重点。
- 将这些值替换为 point—slope 形式,\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写下方程。
找到一条垂直于 x=5 且包含点 (3, −2) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-
再说一遍,既然我们知道一个点,那么点-斜率选项似乎比斜率拦截选项更有前途。 我们需要斜率才能使用这种形式,而且我们知道新线将垂直于 x=5。 这条线是垂直的,所以它的垂直线将是水平的。 这告诉我们\(m_{\perp}=0\).
\(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)
绘制两条线的图形。 它们看起来是垂直的吗?
找出一条垂直于包含点 (4, −5) 的直线 x=4 的方程。 以斜率截距形式写下方程。
- 回答
-
y=−5
找出一条垂直于包含点 (2, −1) 的直线 x=2 的方程。 以斜率截距形式写下方程。
- 回答
-
y=−1
在练习中\(\PageIndex{31}\),我们使用点-斜率形式来求方程。 我们可以用不同的方式来看待这个问题。
我们想找到一条垂直于 x=5 且包含点 (3, −2) 的直线。 该图向我们显示了直线 x=5 和点 (3, −2)。
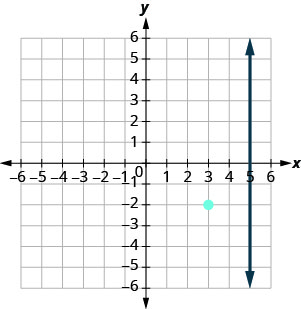
我们知道垂直于垂直线的每条线都是水平的,因此我们将绘制穿过的水平线 (3, −2)。
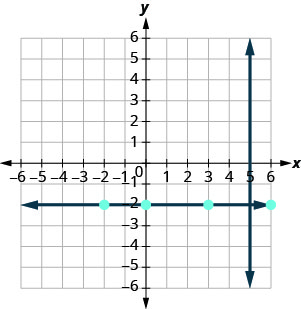
线条看起来是垂直的吗?
如果我们观察这条水平线上的几个点,我们会注意到它们的 y 坐标都为 −2。 因此,垂直于垂直线 x=5 的直线的方程为 y=−2。
找一个垂直于 y=−4 且包含点 (−4,2) 的直线的方程。 以斜率截距形式写下方程。
- 回答
-
y=−4 线是一条水平线。 与之垂直的任何直线都必须是垂直的,形式为 x=a。由于垂直线是垂直且穿过 (−4,2),因此其上的每个点的 x 坐标均为 −4。 垂直线的方程为 x=−4。 你可能想画出线条。 它们看起来是垂直的吗?
找出一条垂直于包含点 (−5,1) 的直线 y=1 的方程。 以斜率截距形式写下方程。
- 回答
-
x=−5
找出一条垂直于包含点 (−4, −5) 的直线 y=−5 的方程。
- 回答
-
x=−4
关键概念
- 在给定斜率和点的情况下求直线方程
- 确定斜率。
- 找出重点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写出方程。
- 求给定两点的直线方程
- 使用给定的点找出斜率。
- 选择一个点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写出方程。
- 书写和直线方程
- 如果给定斜率和\(y\)截距,则使用斜率截距形式\(y=mx+b\)。
- 如果给定斜率和点,则使用点-斜率形式\(y−y_{1}=m(x−x_{1})\)。
- 如果给定两个点,则使用点-斜率形式\(y−y_{1}=m(x−x_{1})\)。
- 求平行于给定直线的直线的方程
- 找出给定直线的斜率。
- 找出平行线的斜率。
- 找出重点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写出方程。
- 求一条垂直于给定直线的直线的方程
- 找出给定直线的斜率。
- 找出垂直线的斜率。
- 找出重点。
- 将这些值替换为点斜率形式,即\(y−y_{1}=m(x−x_{1})\)。
- 以斜率截距形式写出方程。
词汇表
- 点-斜率表单
- 斜率为 mm 且包含点的直线方程的点-斜率形式\(\left(x_{1}, y_{1}\right)\)为\(y-y_{1}=m\left(x-x_{1}\right)\)。


