4.5:使用直线方程的 Slope—Intercept 形式
- Page ID
- 204661
在本节结束时,您将能够:
- 识别图形与直线方程的坡度截距形式之间的关系
- 识别直线方程的斜率和 y 截距形式
- 使用斜率和截距绘制直线图
- 选择最方便的方法来绘制线条
- 绘制和解释坡度截距的应用
- 使用斜率识别平行线
- 使用斜率识别垂直线
识别图形与直线方程的斜率截距形式之间的关系
我们通过绘制点、使用截距、识别水平线和垂直线以及使用点斜率法绘制了线性方程式。 一旦我们看到了斜率截距形式的方程及其图形之间的关系,我们就有另一种方法可以用来绘制线条。
在绘制两个变量中的线性方程中,我们\(y=12x+3\)通过绘制点来绘制方程的直线。 参见图\(\PageIndex{1}\)。 让我们找出这条线的斜率。
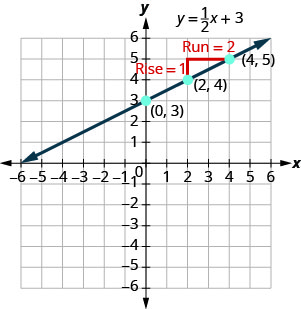
红线向我们显示的是上升\(1\)和跑步\(2\)。 代入斜率公式:
\[\begin{aligned} m &=\frac{\text { rise }}{\text { rise }} \\ m &=\frac{1}{2} \end{aligned}\]
这条\(y\)线的截距是多少? \(y\)-截距是直线与-\(y\) axis 交叉的地方,所以\(y\)-intercept 是\((0,3)\)。 这条线的方程为:
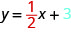
注意,这条线有:

当求解线性方程时\(y\),\(x\)-项的系数是斜率,常量项是\(y\)-\(y\) intercept的-坐标。 我们说方程\(y=\frac{1}{2}x+3\)是斜率截距形式。
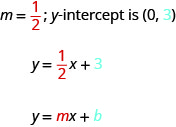
斜率为 mm 和\(y\)-intercept 的直线方程的斜率截距形式\((0,b)\)为
\[y=mx+b\]
有时,斜率截距形式被称为 “y-f orm”。
使用图表找出直线的斜率和\(y\)截距\(y=2x+1\)。
将这些值与方程进行比较\(y=mx+b\)。
- 回答
-
要找到直线的斜率,我们需要在这条线上选择两个点。 我们将使用积分\((0,1)\)和\((1,3)\).
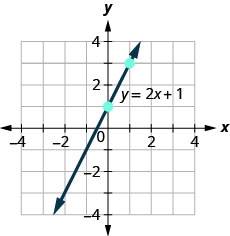
找到上升点然后逃跑。 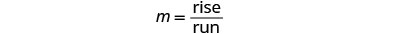
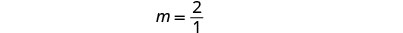
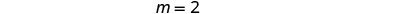
找到直线的\(y\)截距。 \(y\)-截距是重点\((0, 1)\)。 
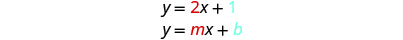
斜率与的系数相同,\(x\)并且\(y\)-\(y\) intercept的-坐标与常量项相同。
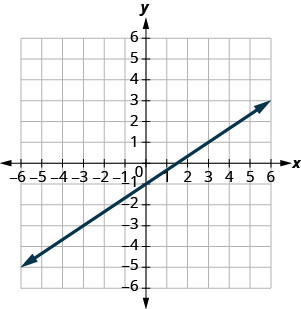
使用图表找出直线的斜率和\(y\)截距\(y=\frac{2}{3}x−1\)。 将这些值与方程进行比较\(y=mx+b\)。
- 回答
-
斜\(y\)率\(m = \frac{2}{3}\)和截距\((0,−1)\)
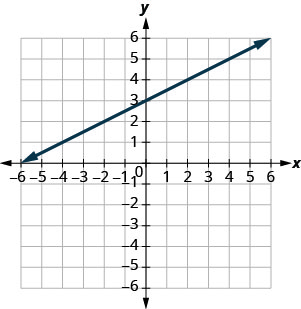
使用图表找出直线的斜率和\(y\)截距\(y=\frac{1}{2}x+3\)。 将这些值与方程进行比较\(y=mx+b\)。
- 回答
-
斜\(y\)率\(m = \frac{1}{2}\)和截距\((0,3)\)
从直线方程中识别斜率和\(y\)截距
在 “了解直线的[1]斜率” 中,我们使用斜率和点绘制了一条直线。 当我们得到一个斜率截距形式的方程时,我们可以使用\(y\)-intercept作为点,然后从那里计算出斜率。 让我们练习从直线方程中求出斜率和\(y\)截距的值。
用方程确定直线的斜率和\(y\)截距\(y=−3x+5\)。
- 回答
-
我们将方程与方程的坡度截距形式进行比较。
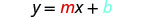
写下直线的方程式。 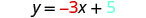
确定斜率。 
识别\(y\)截距。 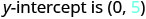
确定直线的斜率和\(y\)截距\(y=\frac{2}{5}x−1\)。
- 回答
-
\(\frac{2}{5}\); (0, −1)
确定直线的斜率和\(y\)截距\(y=−\frac{4}{3}x+1\)。
- 回答
-
\(-\frac{4}{3}\); (0,1)
当直线的方程没有以斜率截距的形式给出时,我们的第一步将是求解方程\(y\)。
用方程确定直线的斜率和\(y\)截距\(x+2y=6\)。
- 回答
-
此方程不是斜率截距形式。 为了将其与斜率截距形式进行比较,我们必须首先求解方程\(y\)。
求解\(y\)。 \(x+2y=6\) 从两边减去 x。 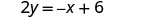
将两边除以\(2\)。 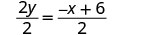
简化。 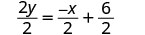
(记住:\(\frac{a+b}{c} = \frac{a}{c} + \frac{b}{c}\)) 简化。 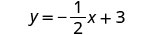
写下直线方程的斜率截距形式。 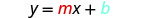
写下直线的方程式。 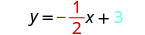
确定斜率。 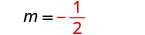
识别\(y\)截距。 
确定直线的斜率和\(y\)截距\(x+4y=8\)。
- 回答
-
\(-\frac{1}{4}\);( 0,2)
确定直线的斜率和\(y\)截距\(3x+2y=12\)。
- 回答
-
\(-\frac{2}{3}\);( 0,6)
使用斜率和截距绘制直线图
现在我们知道如何从直线的方程中找到直线的斜率和\(y\)截距,我们可以通过绘制\(y\)-intercept然后使用斜率找到另一个点来绘制直线的图形。
\(y=4x−2\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-


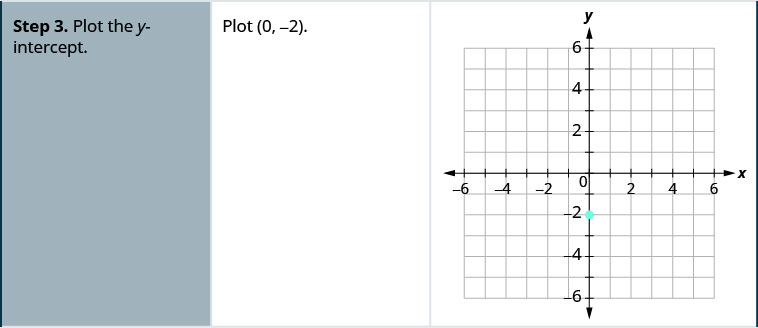

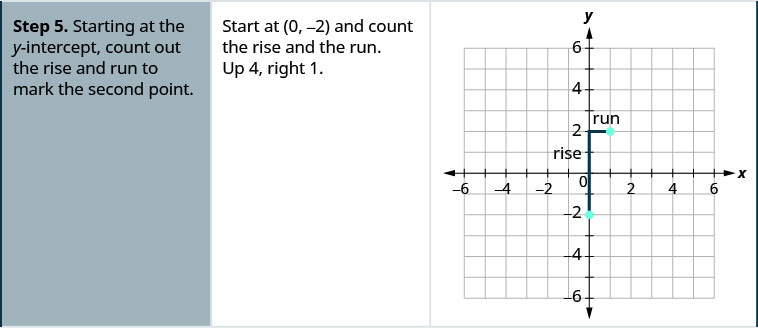
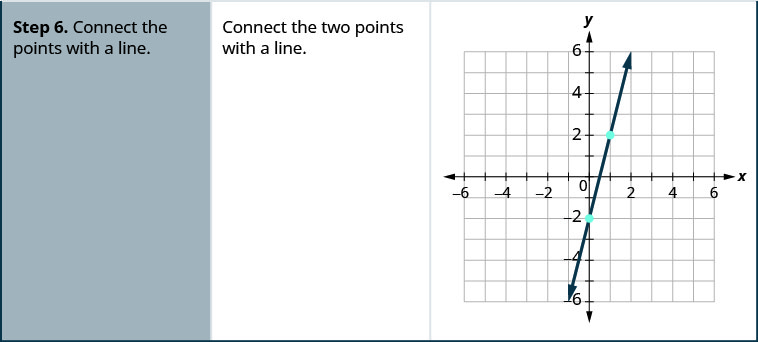
\(y=4x+1\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
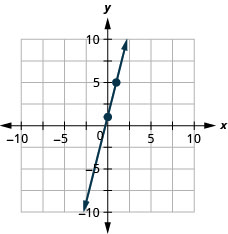
\(y=2x−3\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
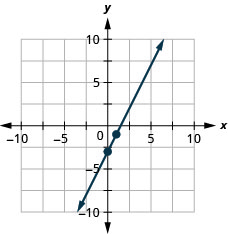
- 找出直线方程的坡度截距形式。
- 识别斜率和\(y\)截距。
- 绘\(y\)制截距。
- 使用斜率公式\(\frac{\text{rise}}{\text{run}}\)来确定上升和游程。
- 从\(y\)-intercept 开始,计算上升次数,然后跑到第二个点。
- 用直线连接各点。
\(y=−x+4\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
检查。\(y=mx+b\) 方程采用斜率截距形式。 \(y=−x+4\) 识别斜率和\(y\)截距。 \(m=−1\) \(y\)-截距是\((0, 4)\) 绘\(y\)制截距。 见下图。 确定上升和奔跑。 \(m = \frac{-1}{1}\) 计算出上升幅度,然后跑到第二个点。 上升\(−1\),跑\(1\) 画出这条线。 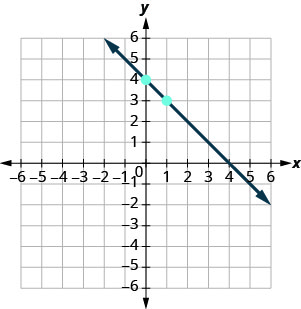
要检查你的工作,你可以在直线上找到另一个点,并确保它是方程的解。 在图表中,我们可以看到直线穿过\((4, 0)\)。 - \(\begin{array}{l}{y=-x+4} \\ {0\stackrel{?}{=}-4+4} \\ {0=0\checkmark}\end{array}\)
\(y=−x−3\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
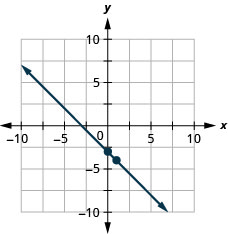
\(y=−x−1\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
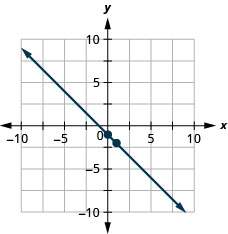
\(y=−\frac{2}{3}x−3\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
\(y=mx+b\) 方程采用斜率截距形式。 \(y=−\frac{2}{3}x−3\) 识别斜率和\(y\)截距。 \(m = -\frac{2}{3}\);\(y\)-截距是\((0, −3)\) 绘\(y\)制截距。 见下图。 确定上升和奔跑。 计算出上升幅度,然后跑到第二个点。 画出这条线。 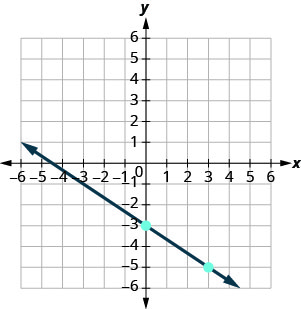
\(y=−\frac{5}{2}x+1\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
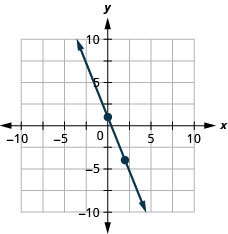
\(y=−\frac{3}{4}x−2\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
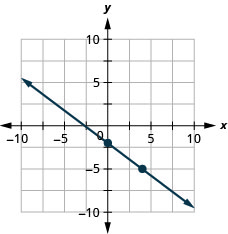
\(4x−3y=12\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
\(4x−3y=12\) 找出方程的坡度截距形式。 \(−3y=−4x+12\) \(−\frac{3y}{3}=\frac{−4x+12}{−3}\) 方程现在采用斜率截距形式。 \(y=\frac{4}{3}x−4\) 识别斜率和\(y\)截距。 \(m=\frac{4}{3}\) \(y\)-ntercept 是\((0, −4)\) 绘\(y\)制截距。 见下图。 确定上升和跑步;计算上涨并跑步以标记第二个点。 画出这条线。 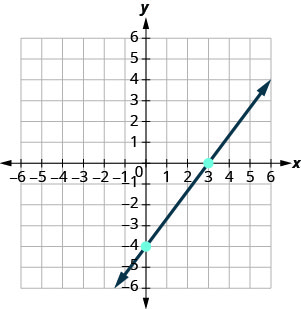
\(2x−y=6\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
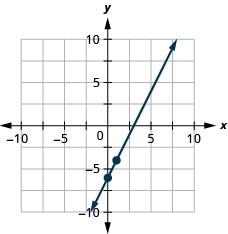
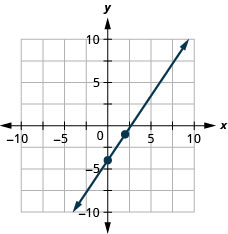
\(3x−2y=8\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
对于到目前为止我们绘制的所有方程,我们\(y\)都使用了\(−10\)网格,两者都从差不多变\(10\)为网格。\(x\) 并非所有的线性方程都可以在这个小网格上绘制出来。 通常,尤其是在使用真实数据的应用程序中,我们需要将轴扩展到更大的正数或更小的负数。
\(y=0.2x+45\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
我们将使用坐标轴从大概\(−80\)到的网格\(80\)。
\(y=mx+b\) 方程采用斜率截距形式。 \(y=0.2x+45\) 识别斜率和\(y\)截距。 \(m=0.2\) \(y\)-截距是\((0, 45)\) 绘\(y\)制截距。 见下图。 计算出上升幅度,然后跑到第二个点。 斜率为\(m=0.2\);以分数形式表示\(m=\frac{2}{10}\)。 考虑到我们图表的比例,使用等效分数会更容易\(m=\frac{10}{50}\)。 画出这条线。 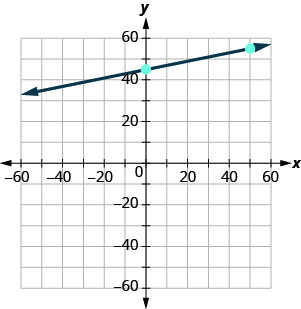
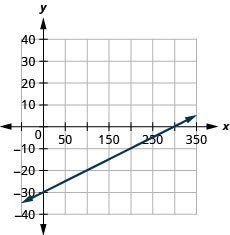
\(y=0.5x+25\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
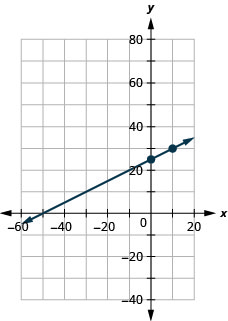
\(y=0.1x−30\)使用方程的斜率和\(y\)截距绘制方程的直线。
- 回答
-
现在我们已经使用斜率和\(y\)截距绘制了线条,让我们总结一下我们用来绘制线条的所有方法。 参见图\(\PageIndex{2}\)。

选择最方便的方法来绘制线条
既然我们已经看到了几种可以用来绘制线条的方法,那么我们怎么知道给定方程使用哪种方法呢?
虽然我们可以绘制点,使用斜率截距形式,或者找到任何方程的截距,但如果我们认识到绘制某种类型方程的最便捷方式,我们的工作就会更容易。 通常,绘制点不是绘制线条的最有效方法。 我们在第 4.3、4.4 节和本节之前的部分中看到了更好的方法。 让我们寻找一些模式来帮助确定绘制线条的最便捷方法。
以下是我们在本章中绘制的六个方程以及我们用来绘制每个方程的方法。
\[\begin{array}{lll}{\text{#1}}&{\text {Equation }} & {\text { Method }} \\ {\text{#2}}&{x=2} & {\text { Vertical line }} \\ {\text{#3}}&{y=4} & {\text { Hortical line }} \\ {\text{#4}}&{-x+2 y=6} & {\text { Intercepts }} \\ {\text{#5}}&{4 x-3 y=12} & {\text { Intercepts }} \\ {\text{#6}}&{y=4 x-2} & {\text { Slope-intercept }} \\{\text{#7}}& {y=-x+4} & {\text { Slope-intercept }}\end{array}\]
方程 #1 和 #2 各只有一个变量。 请记住,在这种形式的方程中,那个变量的值是恒定的;它不依赖于另一个变量的值。 这种形式的方程具有垂直线或水平线的图形。
在方程 #3 和 #4 中,\(x\)和\(y\)都位于方程的同一边。 这两个方程的形式为\(Ax+By=C\)。 我们用它\(y=0\)来找到\(x\)-intercept和\(x=0\)\(y\)-intercept,然后通过为\(x\)或选择另一个值来找到第三个点\(y\)。
方程 #5 和 #6 以斜率截距形式书写。 在确定了方程中的斜率和\(y\)截距之后,我们用它们绘制了直线图。
这导致了以下策略。
考虑方程的形式。
- 如果它只有一个变量,则它是一条垂直线或水平线。
- \(x=a\)是一条穿过\(x\)-axis 的垂直线\(a\)。
- \(y=b\)是一条穿过\(y\)-axis 的水平线\(b\)。
- 如果在方程的一侧\(y\)是孤立的,则以形式\(y=mx+b\)使用斜率和\(y\)-截距绘制图形。
- 确定斜率和\(y\)截距,然后绘制图形。
- 如果方程的形式为\(Ax+By=C\),则找出截距。
- 找到\(x\)-和\(y\)-截距,第三个点,然后绘制图表。
确定绘制每条线的最便捷方法。
- \(y=−6\)
- \(5x−3y=15\)
- \(x=7\)
- \(y=\frac{2}{5}x−1\)。
- 回答
-
1。 \(y=−6\)
这个方程只有一个变量,\(y\)。 它的图形是一条横跨\(y\)-轴的水平线\(−6\)。2。 \(5x−3y=15\)
这个方程的形式是\(Ax+By=C\)。 绘制它的最简单方法是找到拦截点再找一个点。3。 \(x=7\)
只有一个变量,\(x\)。 图形是一条与\(x\)-axis 交叉的垂直线\(7\)。4。 \(y=\frac{2}{5}x−1\)
由于这个方程是\(y=mx+b\)形式上的,因此使用斜率和\(y\)截距绘制这条线最为简单。
确定绘制每条线的最便捷方法:
- \(3x+2y=12\)
- \(y=4\)
- \(y=\frac{1}{5}x−4\)
- \(x=−7\)
- 回答
-
- 截住
- 水平线
- 斜率—截距
- 垂直线
确定绘制每条线的最便捷方法:
- \(x=6\)
- \(y=−\frac{3}{4}x+1\)
- \(y=−8\)
- \(4x−3y=−1\)
- 回答
-
- 垂直线
- 斜率—截距
- 水平线
- 截住
绘制和解释坡度截距的应用
许多现实世界中的应用程序都是通过线性方程建模的。 我们将在这里介绍一些应用程序,这样你就可以看到以斜率截距形式书写的方程与现实情况有何关系。
通常,当线性方程对实际情况进行建模时,变量使用不同的字母,而不是\(x\)和\(y\)。 变量名称提醒我们正在测量的数量。
\(F=\frac{9}{5}C+32\)该方程用于将摄氏度上的温度转换为华氏度上的温度。\(C\)\(F\)
- 找出摄氏温度为的华氏温度\(0\)。
- 找出摄氏温度为的华氏温度\(20\)。
- 解释方程的斜率和\(F\)截距。
- 绘制方程图。
- 回答
-
1。 \(\begin{array}{ll}{\text { Find the Fahrenheit temperature for a Celsius temperature of } 0 .} & {F=\frac{9}{5} C+32} \\ {\text { Find } F \text { when } C=0 .} & {F=\frac{9}{5}(0)+32} \\ {\text { Simplify. }} & {F=32}\end{array}\)
2。 \ begin {array} {ll} {\ text {查找摄氏温度为} 20 时的华氏温度。} & {F=\ frac {9} {5} C+32}\\ {\ text {Find} F\ text {when} C=20。} & {F=\ frac {9} {5} (20) +32}\\ {\ text {Simplify。}} & {F=36+32}\\ {\ text {Simplify。}} & {F=68}\ end {array}
3。 解释方程的斜率和\(F\)截距。
尽管此方程使用\(F\)和\(C\),但仍采用斜率截距形式。
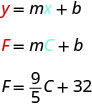
斜率表示当温度摄氏度 (\(F\)) 升高\(9\)度时,温度华氏度 (\(C\)) 会增加\(5\)度数。\(\frac{9}{5}\)
\(F\)-intercept 表示当\(0°\)温度达到摄氏度时,它在华氏度\(32°\)上。
4。 绘制方程图。
我们需要使用比平时更大的比例。 从\(F\)-intercept 开始,\((0,32)\)然后计算上升\(9\)和跑步\(5\)以获得第二个积分。 参见图\(\PageIndex{3}\)。
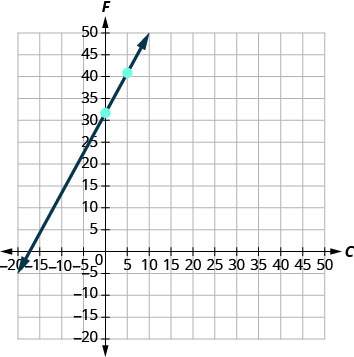
图\(\PageIndex{3}\)
该方程\(h=2s+50\)用于估计女性的身高(以英寸为单位)\(h\),, 根据她的鞋码,\(s\).
- 估算穿女鞋尺码的孩子的身高\(0\)。
- 用鞋子尺码估算女性的身高\(8\)。
- 解释方程的斜率和\(h\)截距。
- 绘制方程图。
- 回答
-
- \(50\)英寸
- \(66\)英寸
- 斜率表示当鞋子尺码增加时\(h\)\(s\),身高会增加\(2\)英寸\(1\)。\(2\) \(h\)-截距表示当鞋码为时\(0\),高度为\(50\)英寸。
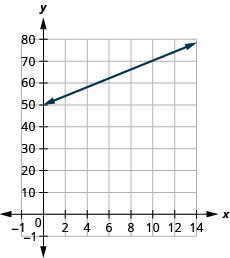
该方程\(T=\frac{1}{4}n+40\)用于根据蟋蟀 chirps 的数量估算一分钟内的温度(以华氏度为单位)。\(T\)\(n\)
- 估计没有啁时的温度。
- 当一分钟内啁的次数为时,估计温度\(100\)。
- 解释方程的斜率和\(T\)截距。
- 绘制方程图。
- 回答
-
- \(40\)度
- \(65\)度
- 斜率表示当啁的数量增加\(1\)时,温度华氏度 (\(F\)) 会增加\(n\)度\(4\)。\(\frac{1}{4}\) \(T\)-intercept 表示当啁数为时\(0\),温度为\(40°\)。
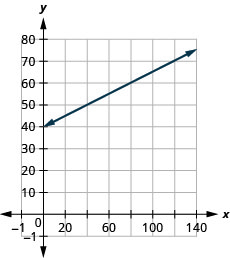
经营某些类型的业务的成本有两个组成部分—— 固定成本和可变成本。 无论生产多少单位,固定成本始终相同。 这是必须定期支付的租金、保险、设备、广告和其他物品的费用。 可变成本取决于生产的单位数量。 它用于生产每件物品所需的材料和人力。
斯特拉有一家出售美味披萨的家庭企业。 该方程\(C=4p+25\)模拟了她每周成本(以美元计)与她销售的披萨数量之间的关系。\(C\)\(p\)
- 找出Stella一周不卖披萨的费用。
- 找出她卖\(15\)披萨一周的费用。
- 解释方程的斜率和\(C\)截距。
- 绘制方程图。
- 回答
-
1。 找出Stella一周不卖披萨的费用。 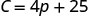
找出\(C\)时间\(p=0\)。 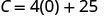
简化。 
斯特拉的固定成本是她不卖披萨\($25\)的时候。 2。 找出她卖\(15\)披萨一周的费用。 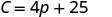
找出\(C\)时间\(p=15\)。 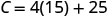
简化。 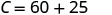

斯特拉的费用是她卖\(15\)披萨\($85\)的时候。 3。 解释方程的斜率和\(C\)截距。 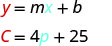
斜率意味着斯特拉每卖一个披萨,成本就会增加。\(4\)\($4\) \(C\)-intercept 意味着,即使 Stella 不卖披萨,她本周的费用也是如此\($25\)。 4。 绘制方程图。 我们需要使用比平时更大的比例。 从\(C\)-intercept 开始,\((0, 25)\)然后计算上升\(4\)和跑步\(1\)以获得第二个积分。 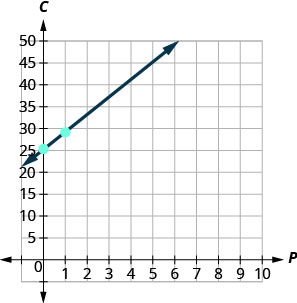
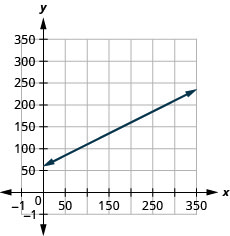
山姆开着一辆送货车。 该方程\(C=0.5m+60\)模拟了他每周的成本(以美元为单位)与他行驶的里程数之间的关系。\(C\)\(m\)
- 查出 Sam 行驶\(0\)里程一周的费用。
- 找出他行驶\(250\)里程一周的费用。
- 解释方程的斜率和\(C\)截距。
- 绘制方程图。
- 回答
-
- \($60\)
- \($185\)
- 斜率表示当行驶里程数增加\($0.50\)时\(n\),每周成本增加\(1\)。\(0.5\)\(C\) \(C\)-intercept 表示当行驶里程数为时\(0\),每周成本为\($60\)。
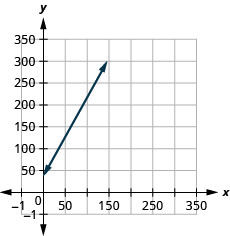
洛琳有一家书法生意。 该方程式\(C=1.8n+35\)模拟了她每周的费用(以美元计)与她写的结婚\(n\)请柬数量之间的关系。\(C\)
- 查看 Loreen 没有写邀请函时一周的费用。
- 找出她写\(75\)邀请函一周的费用。
- 解释方程的斜率和\(C\)截距。
- 绘制方程图。
- 回答
-
- \($35\)
- \($170\)
- 斜率表示当邀请数量增加\($1.80\)时\(C\),每周费用会增加\(1.80\)。\(1.8\)\(n\) \(C\)-intercept 表示当邀请数量为时\(0\),每周费用为\($35\)。
使用斜率识别平行线
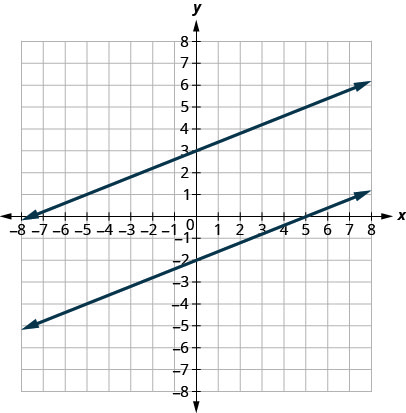
直线的斜率表示这条线的陡峭程度,以及我们从左到右读取时它是上升还是下降。 两条具有相同斜率的线称为平行线。 平行线从不相交。

垂直线呢? 垂直线的斜率未定义,因此垂直线不符合上述定义。 我们说具有不同\(x\)-intercepts的垂直线是平行的。 参见图\(\PageIndex{5}\)。
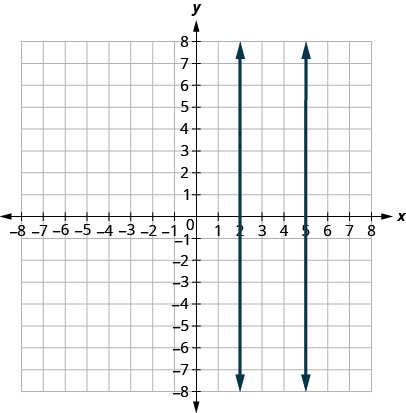
平行线是同一平面中不相交的线。
- 平行线具有相同的斜率和不同的\(y\)截距。
- 如果\(m_{1}\)和\(m_{2}\)是两条平行线的斜率,那么\(m_{1} = m_{2}\)。
- 平行垂直线有不同的\(x\)截距。
让我们在同一个网格\(2x+y=−1\)上绘\(y=−2x+3\)制方程式。 第一个方程已经采用斜率截距形式:\(y=−2x+3\). 我们求解第二个方程为\(y\):
\[\begin{aligned} 2x+y &=-1 \\ y &=-2x-1 \end{aligned}\]
绘制线条图。
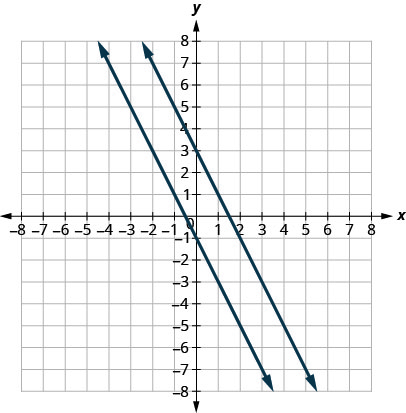
注意线条看起来是平行的。 每条线的斜率是多少? 每行的\(y\)截距是多少?
\[\begin{array}{lll} {y} & {=m x+b} & {y=m x+b} \\ {y} & {=-2 x+3} & {y=-2 x-1} \\ {m} & {=-2} & {m=-2}\\ {b} & {=3,(0,3)} & {b=-1,(0,-1)}\end{array}\]
直线的斜率相同,每条\(y\)线的截距不同。 所以我们知道这些线是平行的。
由于平行线具有相同的斜率和不同的\(y\)截距,我们现在可以只看直线方程的斜率-截距形式,然后决定线是否平行。
使用斜率和\(y\)截距来确定直线\(3x−2y=6\)和\(y = \frac{3}{2}x + 1\)是否平行。
- 回答
-
\(\begin{array} {lrll} {\text { Solve the first equation for } y .} &{ 3 x-2 y} &{=} &{6}\\{} & {\frac{-2 y}{-2}} &{ =}&{-3 x+6 }\\ {} &{\frac{-2 y}{-2}}&{ =}&{\frac{-3 x+6}{-2}} \\ {} & {y }&{=}&{\frac{3}{2} x-3} \end{array}\)
方程现在采用斜率截距形式。
第二条线的方程已经采用斜率截距形式。
确定两条线的斜率和\(y\)截距。
\(\begin{array}{lll}{y=\frac{3}{2} x+1} & {} & {y=\frac{3}{2} x-3} \\ {y=m x+b} & {} & {y=m x+b}\\ {m=\frac{3}{2}} & {} & {m=\frac{3}{2}} \\ {y\text{-intercept is }(0, 1)} & {} & {y\text{-intercept is }(0, −3)} \end{array}\)
这些线具有相同的斜率和不同的\(y\)截距,因此它们是平行的。 您可能需要绘制线条图以确认它们是否平行。
使用斜率和\(y\)截距来确定直线\(2x+5y=5\)和\(y=−\frac{2}{5}x−4\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(4x−3y=6\)和\(y=\frac{4}{3}x−1\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(y=−4\)和\(y=3\)是否平行。
- 回答
-
\(\begin{array}{llll}{\text{Write each equation in slope-intercept form.}} &{y=-4} & {\text { and }} &{ y=3} \\ {\text{Since there is no }x\text{ term we write }0x.} &{y=0 x-4} & {} &{y=0 x+3} \\ {\text{Identify the slope and }y\text{-intercept of both lines.}} &{y=m x+b} &{} & {y=m x+b} \\ {} &{m=0} &{} & {m=0} \\{} & {y\text {-intercept is }(0,4)} &{} & {y \text {-intercept is }(0,3)}\end{array}\)
这些线具有相同的斜率和不同的\(y\)截距,因此它们是平行的。
还有另一种方法可以看这个例子。 如果你立刻从方程中认出它们是水平线,你就知道它们的斜率是两者兼而有之\(0\)。 由于水平线在-at\(y=−4\) 和 at 处穿\(y\)过-axis\(y=3\),所以我们知道\(y\)-intercepts 是\((0,−4)\) and\((0,3)\)。 这些线具有相同的斜率和不同的\(y\)截距,因此它们是平行的。
使用斜率和\(y\)截距来确定直线\(y=8\)和\(y=−6\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(y=1\)和\(y=−5\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(x=−2\)和\(x=−5\)是否平行。
- 回答
-
\[x=-2 \text { and } x=-5\]
既然没有\(y\),方程就不能采用斜率截距形式。 但是我们认为它们是垂直线的方程式。 他们的\(x\)-intercepts 是\(−2\) an\(−5\) d。 由于它们的\(x\)-intercepts不同,因此垂直线是平行的。
使用斜率和\(y\)截距来确定直线\(x=1\)和\(x=−5\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(x=8\)和\(x=−6\)是否平行。
- 回答
-
平行
使用斜率和\(y\)截距来确定直线\(y=2x−3\)和\(−6x+3y=−9\)是否平行。 你可能也想画出这些线条,看看它们是什么样子。
- 回答
-
\(\begin{array} {llll} {\text { The first equation is already in slope-intercept form. }} & {y=2x-3}&{}&{} \\ \\ {\text { Solve the second equation for } y} & {-6x+3y} &{=}&{-9} \\{} & {3y}&{=}&{6x-9} \\ {}&{\frac{3y}{3} }&{=}&{\frac{6x-9}{3}} \\{} & {y}&{=}&{2x-3}\end{array}\)
第二个方程现在也采用了斜率截距形式。
确定两条线的斜率和\(y\)截距。
\[\begin{array}{lll}{y=2x-3} &{} & {y=2x-3} \\ {y=mx+b} &{} & {y=mx+b} \\ {m=2} &{} & {m=2} \\ {\text{The }y\text{-intercept is }(0 ,−3)} &{} & {\text{The }y\text{-intercept is }(0 ,−3)} \end{array} \nonumber\]
这些线的斜率相同,但它们也有相同的\(y\)截距。 它们的方程表示同一条线。 它们不是平行的;它们是同一条线。
使用斜率和\(y\)截距来确定直线\(y=−\frac{1}{2}x−1\)和\(x+2y=2\)是否平行。
- 回答
-
不平行;同一条线
使用斜率和\(y\)截距来确定直线\(y=\frac{3}{4}x−3\)和\(3x−4y=12\)是否平行。
- 回答
-
不平行;同一条线
使用斜率识别垂直线
让我们来看看方程为\(y=\frac{1}{4}x−1\)和的直线\(y=−4x+2\),如图所示\(\PageIndex{5}\)。
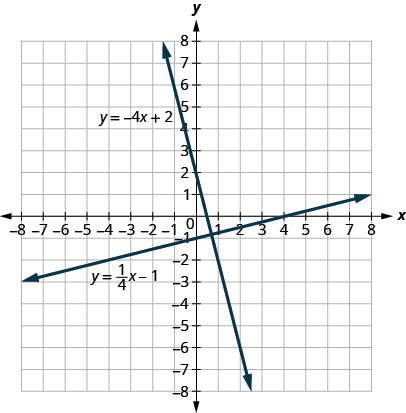
这些线位于同一个平面上,以直角相交。 我们称这些线为垂直。
你对这两条线的斜率有什么看法? 当我们从左至右读取时,该线\(y=14x−1\)上升,因此其斜率为正。 该线从左向右\(y=−4x+2\)下降,因此斜率为负。 两条垂直线的斜率会有相反的符号对你来说有意义吗?
如果我们看第一条线的斜率和第二条线的斜率\(m_{2}=−4\),我们可以看出它们是彼此的负倒数。\(m_{1}=14\) 如果我们乘以它们,它们的乘积就是\(−1\)。
\[\begin{array}{c}{m_{1} \cdot m_{2}} \\ {\frac{1}{4}(-4)} \\ {-1}\end{array}\]
对于垂直线来说,这总是正确的,这使我们得出了这个定义。
垂直线是同一平面上形成直角的直线。
如果 m1 和 m2 是两条垂直线的斜率,则:
\[m_{1} \cdot m_{2}=-1 \text { and } m_{1}=\frac{-1}{m_{2}}\]
垂直线和水平线始终相互垂直。
我们能够观察线性方程的斜率截距形式,并确定这些线是否平行。 我们可以对垂直线做同样的事情。
我们找到方程的斜率截距形式,然后查看斜率是否为负倒数。 如果斜率的乘积为\(−1\),则线是垂直的。 垂直线可能有相同的\(y\)截距。
使用斜率来确定直线\(y=−5x−4\)和\(x−5y=5\)是否垂直。
- 回答
-
第一个方程已经采用斜率截距形式:\(\quad y=−5x−4\)
\(\begin{array} {llll} {\text{Solve the second equation for }y.} &{x-5y} &{=} &{5} \\{} &{-5 y} &{=} &{-x+5} \\ {} & {\frac{-5 y}{-5}} &{=} &{\frac{-x+5}{-5}} \\ {} &{y} &{=} &{\frac{1}{5} x-1} \end{array}\)第二个方程现在也采用了斜率截距形式。
\(\begin{array} {lrllllll} {\text{Identify the slope of each line.}} &{y} &{=} &{-5 x-4} & {} &{y} &{=} &{\frac{1}{5} x-1} \\ {} &{y} &{=} &{m x+b} & {} &{y} &{=} &{m x+b}\\ {} &{m_{1}} &{=}&{-5} & {} &{m_{2}} &{=}&{\frac{1}{5}}\end{array}\)
斜率是彼此的负倒数,因此线是垂直的。 我们通过乘以斜率进行检查,
\[\begin{array}{l}{m_{1} \cdot m_{2}} \\ {-5\left(\frac{1}{5}\right)} \\ {-1\checkmark}\end{array}\]
使用斜率来确定直线\(y=−3x+2\)和\(x−3y=4\)是否垂直。
- 回答
-
垂直
使用斜率来确定直线\(y=2x−5\)和\(x+2y=−6\)是否垂直。
- 回答
-
垂直
使用斜率来确定直线\(7x+2y=3\)和\(2x+7y=5\)是否垂直。
- 回答
-
\(\begin{array}{lrlrl}{\text{Solve the equations for y.}} &{7 x+2 y} & {=3} & {2 x+7 y}&{=}&{5} \\{} & {2 y} & {=-7 x+3} & {7 y}&{=}&{-2 x+5} \\ {} &{\frac{2 y}{2}} & {=\frac{-7 x+3}{2} \quad} & {\frac{7 y}{7}}&{=}&{\frac{-2 x+5}{7}} \\ {} &{y} & {=-\frac{7}{2} x+\frac{3}{2}} &{y}&{=}&{\frac{-2}{7}x + \frac{5}{7}}\\ \\{\text{Identify the slope of each line.}} & {y}&{=m x+b} &{y}&{=}&{m x+b} \\{} & {m_{1}} & {=-\frac{7}{2} }&{ m_{2}}&{=}&{-\frac{2}{7}}\end{array}\)
斜率是彼此的倒数,但它们具有相同的符号。 由于它们不是负倒数,因此线不垂直。
使用斜率来确定直线\(5x+4y=1\)和\(4x+5y=3\)是否垂直。
- 回答
-
不垂直
使用斜率来确定直线\(2x−9y=3\)和\(9x−2y=1\)是否垂直。
- 回答
-
不垂直
关键概念
- 斜率为 mm 和\(y\)-intercept的直线方程的斜率截距形式\((0,b)\)为\(y=mx+b\)。
- 使用斜率和\(y\)截距绘制直线图
- 找出直线方程的坡度截距形式。
- 识别斜率和\(y\)截距。
- 绘\(y\)制截距。
- 使用斜率公式\(m = \dfrac{\text{rise}}{\text{run}}\)来确定上升和游程。
- 从\(y\)-intercept 开始,计算上升次数,然后跑到第二个点。
- 用直线连接各点。
- 选择最便捷的绘制线条方法的策略:考虑方程的形式。
- 如果它只有一个变量,则它是一条垂直线或水平线。
\(x = a\)是一条在 a 处穿过\(x\)-axis 的垂直线。
\(y = b\)是一条穿过\(y\)-axis 的水平线\(b\)。 - 如果在方程的一侧\(y\)是孤立的,则以形式\(y=mx+b\)使用斜率和\(y\)-截距绘制图形。
确定斜率和\(y\)截距,然后绘制图形。 - 如果方程的形式为\(Ax+By=C\),则找出截距。
找到\(x\)-和\(y\)-截距,第三个点,然后绘制图表。
- 如果它只有一个变量,则它是一条垂直线或水平线。
- 平行线是同一平面中不相交的线。
- 平行线具有相同的斜率和不同的\(y\)截距。
- 如果\(m_1\)和\(m_2\)是两条平行线的斜率,那么\(m_1 = m_2\)。
- 平行垂直线有不同的\(x\)截距。
- 垂直线是同一平面上形成直角的直线。
- 如果\(m_1\)和\(m_2\)是两条垂直线的斜率,则\(m_1\cdot m_2=−1\)和\(m_1=\frac{−1}{m_2}\)。
- 垂直线和水平线始终相互垂直。
词汇表
- 平行线
- 同一平面中不相交的线。
- 垂直线
- 在同一平面上形成直角的直线。
- 直线方程的斜率截距形式
- 斜率为 mm 和\(y\)-intercept的直线方程的斜率截距形式\((0,b)\)为\(y=mx+b\)。


