4.4E:练习
- Page ID
- 204697
练习成就完美
使用地理板对坡度进行建模
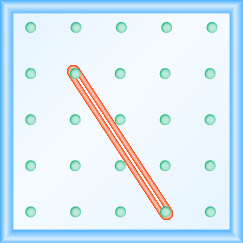
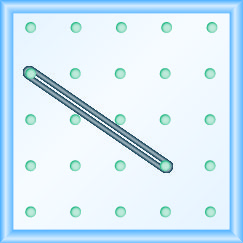
在以下练习中,找到在每个地理板上建模的斜率。
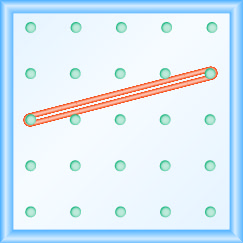
- 回答
-
\(\frac{1}{4}\)
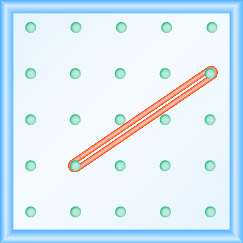
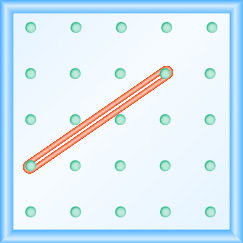
- 回答
-
\(\frac{2}{3}\)
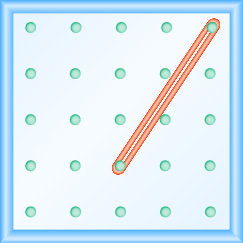
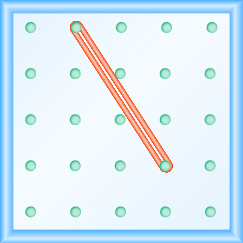
- 回答
-
\(\frac{-3}{2}=-\frac{3}{2}\)
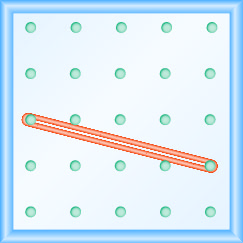
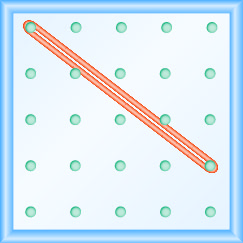
- 回答
-
\(-\frac{2}{3}\)
在以下练习中,对每个斜率进行建模。 画一张照片来显示你的结果。
\(\frac{2}{3}\)
- 回答
-

\(\frac{3}{4}\)
\(\frac{1}{4}\)
- 回答
-

\(\frac{4}{3}\)
\(-\frac{1}{2}\)
- 回答
-

\(-\frac{3}{4}\)
\(-\frac{2}{3}\)
- 回答
-
\(-\frac{3}{2}\)
\(m=\frac{rise}{run}\)用于从曲线图中查找直线的斜率
在以下练习中,找到所示每条线的斜率。
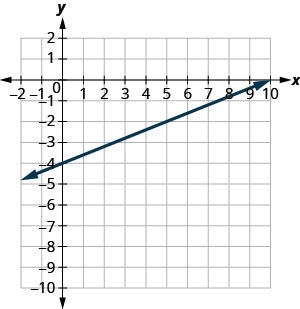
- 回答
-
\(\frac{2}{5}\)
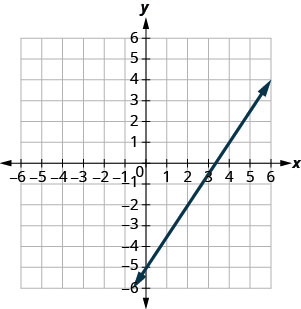
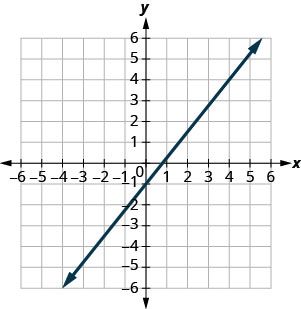
- 回答
-
\(\frac{5}{4}\)
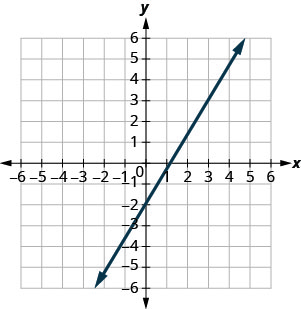
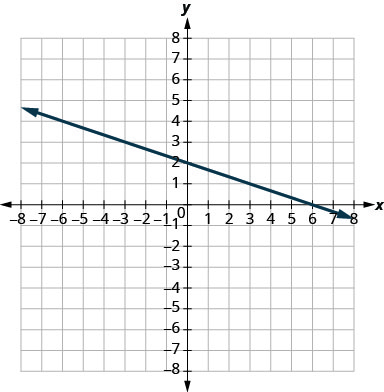
- 回答
-
\(-\frac{1}{3}\)
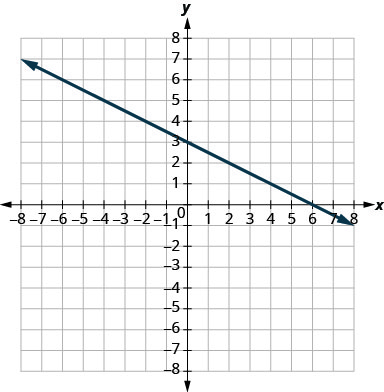
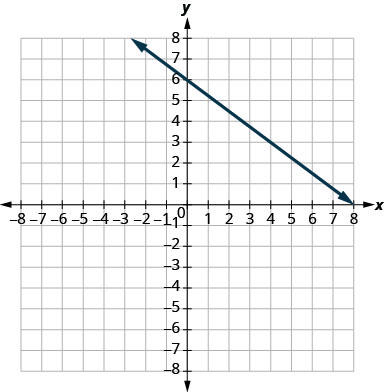
- 回答
-
\(-\frac{3}{4}\)
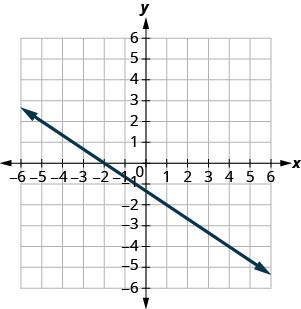
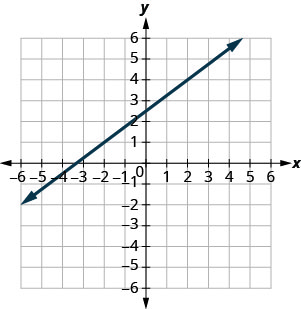
- 回答
-
\(\frac{3}{4}\)
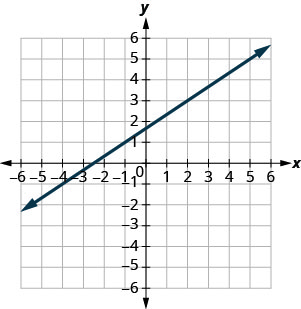
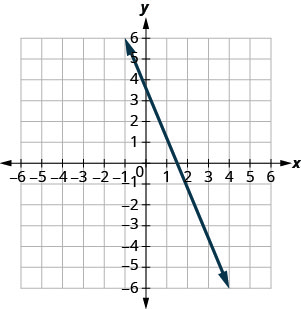
- 回答
-
\(-\frac{5}{2}\)
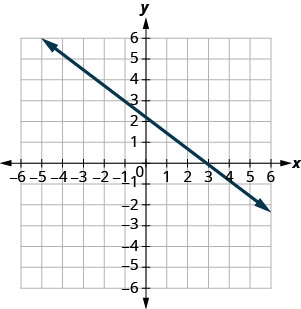
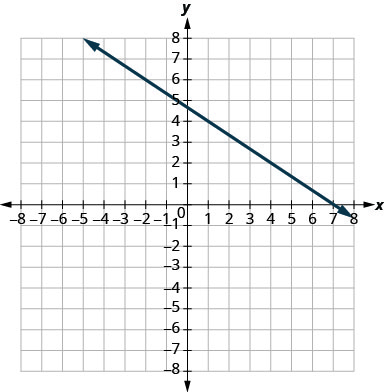
- 回答
-
\(-\frac{2}{3}\)
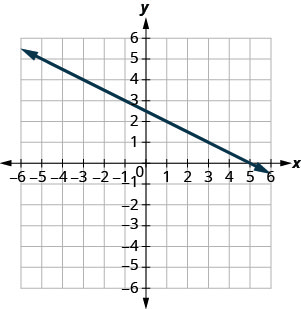
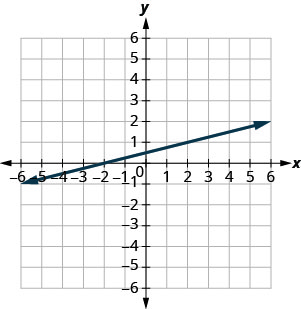
- 回答
-
\(\frac{1}{4}\)
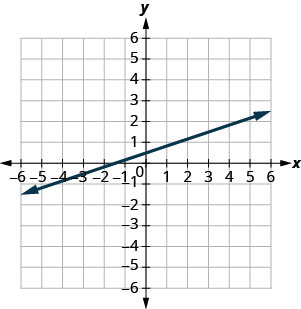
找出水平线和垂直线的斜率
在以下练习中,找出每条线的斜率。
y=3
- 回答
-
0
y=1
x=4
- 回答
-
未定义
x=2
y=−2
- 回答
-
0
y=−3
x=−5
- 回答
-
未定义
x=−4
使用斜率公式求出两点间直线的斜率
在以下练习中,使用斜率公式求出每对点之间的直线的斜率。
(1,4)、(3,9)
- 回答
-
\(\frac{5}{2}\)
(2,3)、(5,7)
(0,3)、(4,6)
- 回答
-
\(\frac{3}{4}\)
(0,1)、(5,4)
(2,5)、(4,0)
- 回答
-
\(-\frac{5}{2}\)
(3,6)、(8,0)
(−3,3)、(4、−5)
- 回答
-
\(-\frac{8}{7}\)
(−2,4)、(3、−1)
(−1, −2), (2,5)
- 回答
-
\(\frac{7}{3}\)
(−2, −1), (6,5)
(4, −5), (1, −2)
- 回答
-
−1
(3, −6), (2, −2)
给定一个点和斜率绘制一条直线
在以下练习中,用给定的点和斜率绘制每条线。
\((1,-2) ; m=\frac{3}{4}\)
- 回答
-
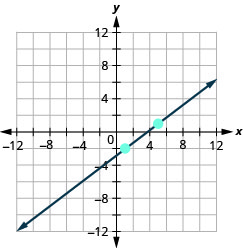
\((1,-1) ; m=\frac{2}{3}\)
\((2,5) ; m=-\frac{1}{3}\)
- 回答
-
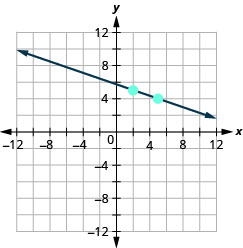
\((1,4) ; m=-\frac{1}{2}\)
\((-3,4) ; m=-\frac{3}{2}\)
- 回答
-
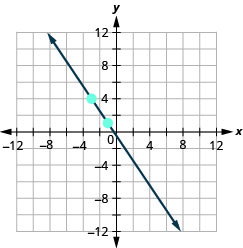
\((-2,5) ; m=-\frac{5}{4}\)
\((-1,-4) ; m=\frac{4}{3}\)
- 回答
-
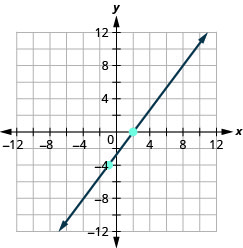
\((-3,-5) ; m=\frac{3}{2}\)
\(y\)-截距\(3 ; m=-\frac{2}{5}\)
- 回答
-
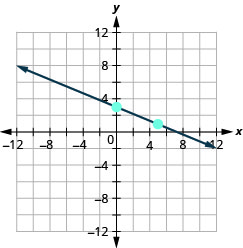
\(y\)-截距\(5 ; m=-\frac{4}{3}\)
\(x\)-截距\(-2 ; m=\frac{3}{4}\)
- 回答
-
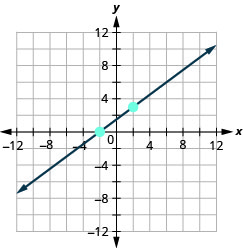
\(x\)-截距\(-1 ; m=\frac{1}{5}\)
\((-3,3) ; m=2\)
- 回答
-
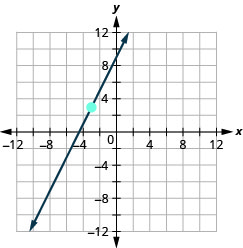
\((-4,2) ; m=4\)
\((1,5) ; m=-3\)
- 回答
-
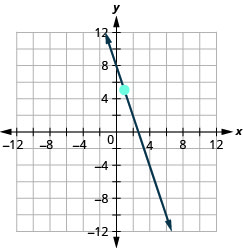
\((2,3) ; m=-1\)
日常数学
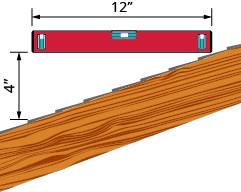
屋顶的坡度。 确定屋顶坡度的一种简单方法是将12英寸水平的一端设置在屋顶表面,并将其保持水平。 然后拿起卷尺或尺子,从楼梯的另一端向下测量到屋顶表面。 这将为您提供屋顶的斜率。 建筑商有时将其称为俯仰并将其表示为 “x 12 pitch” 的意思\(\frac{x}{12}\),其中 x 是从屋顶到水平——上升的测量值。 它有时也被称为 “x-in-12 音高”。
- 这张照片中屋顶的斜率是多少?
- 施工方面的立场是什么?
- 回答
-
- \(\frac{1}{3}\)
- 4 12 音高或 4 合 12 音高
此处显示的屋顶坡度是用 12 英寸的高度和标尺测量的。 这个屋顶的坡度是多少?
道路等级。 当地道路的坡度为 6%。 道路的坡度是以百分比表示的坡度。 以分数形式找到道路的坡度,然后进行简化。 什么上升和跑步会反映这个斜率或坡度?
- 回答
-
\(\frac{3}{50} ;\)上升\(=3,\)跑\(=50\)
公路等级。 每行驶50英尺的高速公路,当地道路上升2英尺。
- 高速公路的坡度是多少?
- 高速公路的坡度是以百分比表示的坡度。 这条高速公路的坡度是多少?
轮椅坡道。 轮椅坡道的规定要求12英寸的跑步最多上升1英寸。
- 坡道需要多长时间才能容纳上升 24 英寸的门口?
- 创建这个坡道的模型。
- 回答
-
- 288 英寸(24 英尺)
- 型号会有所不同。
轮椅坡道。 16 英寸的跑步上升 1 英寸可以让轮椅骑手更容易登上坡道。
- 坡道需要多长时间才能轻松容纳 24 英寸的高度?
- 创建这个坡道的模型。
写作练习
斜坡的标志告诉你关于直线的什么?
- 回答
-
当斜率为正数时,直线从左向右向上移动。 当斜率为负数时,直线从左向右向下移动。
带斜率的直线的图形与带斜率的直线的图形有\(m=\frac{1}{2}\)何不同\(m=2 ?\)
为什么垂直线的斜率 “未定义”?
- 回答
-
垂直线的游程为 0,由于未定义除以 0,因此斜率未定义。
自检
ⓐ 完成练习后,使用这份清单来评估你对本节目标的掌握程度。
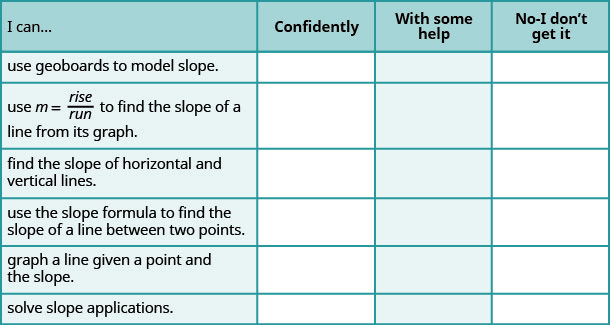
ⓑ 在 1-10 的等级中,根据你在清单上的回复,你会如何评价你对本节的掌握程度? 你怎么能改善这个?
词汇表
- 地理板
- 地理板是指上面有钉子网格的木板。
- 负斜率
- 当你从左向右读取时,直线的负斜率会下降。
- 正斜率
- 当你从左向右读取时,直线的正斜率上升。
- 上升
- 直线的上升是其垂直变化。
- 跑
- 一条线的长度是它的水平变化。
- 斜率公式
- 两点\(\left(x_{1}, y_{1}\right)\)和之间的直线的斜率\(\left(x_{2}, y_{2}\right)\)为\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)。
- 直线的斜率
- 直线的斜率为\(m=\frac{\text { rise }}{\text { run }}\)。 上升衡量垂直变化,运行衡量水平变化。