4.4: 了解直线的斜率
- Page ID
- 204678
- 在本节结束时,您将能够:
- 使用地理板对坡度进行建模
- \(m = \frac{\text{rise}}{\text{run}}\)用于从曲线图中找出直线的斜率
- 找出水平线和垂直线的斜率
- 使用斜率公式求出两点之间直线的斜率
- 给定一个点和斜率绘制一条直线
- 求解斜率应用程序
在开始之前,请参加这个准备测验。
- 简化:\(\frac{1 - 4}{8 - 2}\)。
如果你错过了这个问题,请查看练习 1.6.31 - 除以:\(\frac{0}{4}, \frac{4}{0}\)。
如果您错过了此问题,请查看练习 1.10.16。 - 简化:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\)。
如果您错过了此问题,请查看练习 1.6.4。
当你绘制线性方程时,你可能会注意到有些线条从左向右倾斜,有些线条向下倾斜。 有些线条非常陡峭,有些线条比较平坦。 是什么决定了直线是向上还是向下倾斜,或者是陡峭还是平坦?
在数学中,直线的 “倾斜” 称为直线的斜率。 斜率的概念在现实世界中有许多应用。 屋顶的间距、高速公路的坡度以及轮椅的坡道就是一些你真正看到斜坡的例子。 当你骑自行车时,当你上坡或下坡时,你会感觉到斜坡。
在本节中,我们将探讨斜率的概念。
使用地理板对坡度进行建模
地理板是指上面有钉子网格的木板。 在地理板上使用橡皮筋为我们提供了一种在坐标网格上对线进行建模的具体方法。 通过在地理板上的两个钉子之间拉一根橡皮筋,我们可以发现如何找到直线的斜率。
进行操纵数学活动 “探索斜坡” 将有助于你更好地理解直线的斜率。 (如果需要,可以使用方格纸代替地理板。)我们首先在两个钉子之间拉一根橡皮筋,如图所示\(\PageIndex{1}\)。
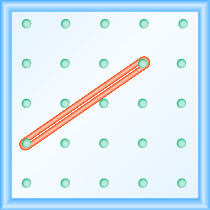
它看起来不像一条线吗?
现在,我们将橡皮筋的一部分从左钉直接向上拉伸,然后绕第三个钉子拉伸,形成直角三角形的两侧,如图所示\(\PageIndex{2}\)
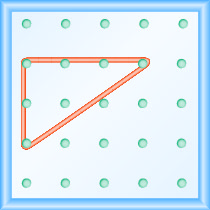
我们小心翼翼地围绕第三个钉子画出 90º 的角度,因此其中一条新形成的线是垂直的,另一条是水平的。
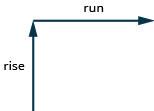
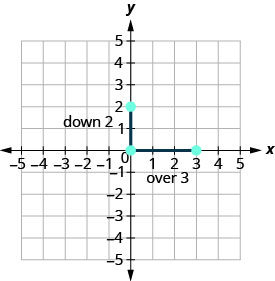
为了找到直线的斜率,我们测量了沿三角形垂直和水平边的距离。 垂直距离称为上升,水平距离称为跑步,如图所示\(\PageIndex{3}\)。
如果我们的地理板和橡皮筋看起来与图中所示相同\(\PageIndex{4}\),则上升幅度为 2。 橡皮筋上升 2 个单位。 (每个空间是一个单位。)
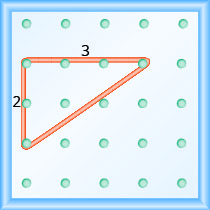
这个地理板的上升幅度为 2,因为橡皮筋上升了两个单位。
跑步是什么?
橡皮筋横穿 3 个单元。 运行为 3(参见图\(\PageIndex{4}\))。
直线的斜率是上升与游程的比率。 在数学中,它总是用字母 m 来表示。
一条直线的斜率为\(m = \frac{\text{rise}}{\text{run}}\)。
上升测量垂直变化,跑步测量直线上两点之间的水平变化。
图中地理板上线的斜率是多\(\PageIndex{4}\)少?
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]
这条线有斜率\(\frac{2}{3}\)。 这意味着该线每运行 3 个单位就会增加 2 个单位。
当我们使用地理板时,最好养成从左边的钉子开始,然后连接到右边的钉子的习惯。 如果上升是正数,如果下降则为负值。 跑步将从左向右移动,为正值。
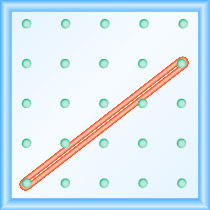
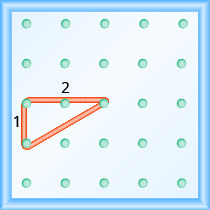
所示地理板上线的斜率是多少?
- 回答
-
使用斜率的定义:\(m = \frac{\text{rise}}{\text{run}}\).
从左边的钉子开始,向上和向右计算空格以到达第二个钉子。
\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]
这意味着该线每运行 4 个单位就会增加 3 个单位。
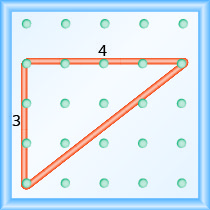
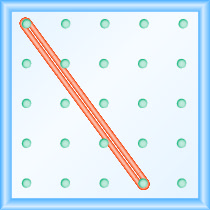
所示地理板上线的斜率是多少?
- 回答
-
\(\frac{4}{3}\)
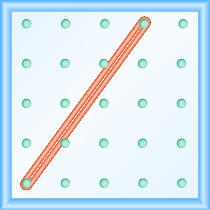
所示地理板上线的斜率是多少?
- 回答
-
\(\frac{1}{4}\)
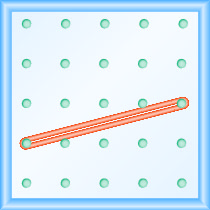
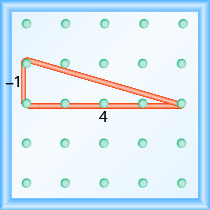
所示地理板上线的斜率是多少?
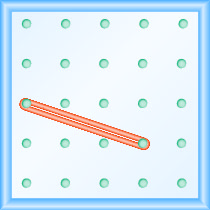
- 回答
-
使用斜率的定义:\(m = \frac{\text{rise}}{\text{run}}\).
从左钉开始,向下计数单位,向右计数以到达第二个钉子。
\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]
这意味着该线每运行 3 个单位就会掉落 1 个单位。
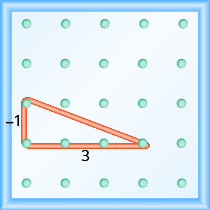
地理板上线的斜率是多少?
- 回答
-
\(-\frac{2}{3}\)
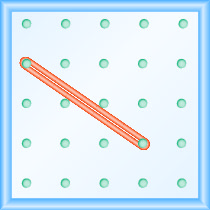
地理板上线的斜率是多少?
- 回答
-
\(-\frac{4}{3}\)
请注意,在练习\(\PageIndex{1}\)中,斜率为正,而在练习\(\PageIndex{4}\)中,斜率为负。 你注意到图 (a) 和图 (b) 所示的两行有什么区别吗?
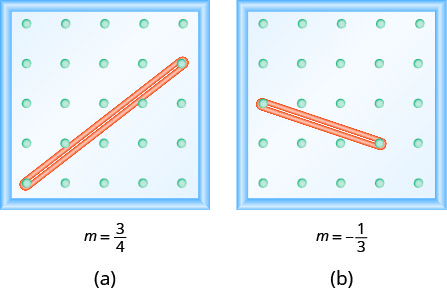
我们从左到右 “读” 一行,就像我们读英语单词一样。 当你从左向右读取时,图 (a) 中的线条正在向上移动;它有正斜率。 图 (b) 中的线正在向下;它的斜率为负。

使用地理板对带有斜率的线进行建模\(\frac{1}{2}\)。
- 回答
-
要在地理板上对直线进行建模,我们需要上升和奔跑。
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)
由橡皮筋形成的直角三角形的斜边代表斜率为的线\(\frac{1}{2}\)。
对斜率进行建模\(m = \frac{1}{3}\)。 画一张照片来显示你的结果。
- 回答
-
对斜率进行建模\(m = \frac{3}{2}\)。 画一张照片来显示你的结果。
- 回答
-

使用地理板对带有斜率的线进行建模\(\frac{-1}{4}\)。
- 回答
-
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)
由橡皮筋形成的直角三角形的斜边代表斜率为的线\(\frac{-1}{4}\)。
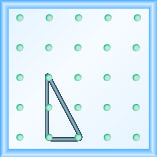
对斜率进行建模\(m = \frac{-2}{3}\)。 画一张照片来显示你的结果。
- 回答
-
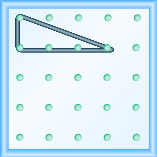
对斜率进行建模\(m = \frac{-1}{3}\)。 画一张照片来显示你的结果。
- 回答
-
\(m = \frac{\text{rise}}{\text{run}}\)用于从曲线图中找出直线的斜率
现在,我们来看看 xy 坐标平面上的一些图表,看看如何找到它们的斜率。 该方法将与我们刚刚在地理板上建模的方法非常相似。
要找到斜坡,我们必须计算上升和跑步。 但是我们从哪里开始呢?
我们在坐标为整数的直线上找到两个点。 然后我们从左边的点开始,画一个直角三角形,这样我们就可以计算上升和跑步了。
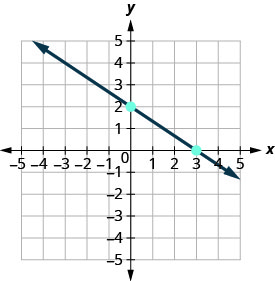
找到所示直线的斜率。
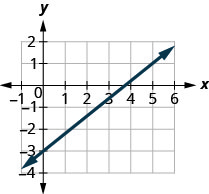
- 回答
-



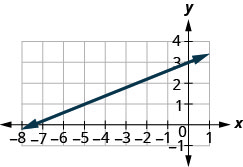
找到所示直线的斜率。
- 回答
-
\(\frac{2}{5}\)
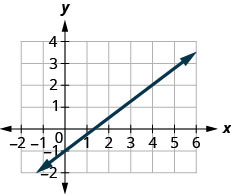
找到所示直线的斜率。
- 回答
-
\(\frac{3}{4}\)
- 在坐标为整数的直线上找到两个点。
- 从左边的点开始,画一个从第一个点到第二个点的右三角形。
- 计算三角形腿上的上升和跑步。
- 取上升与跑步的比率来找到斜率,\(m = \frac{\text{rise}}{\text{run}}\)。
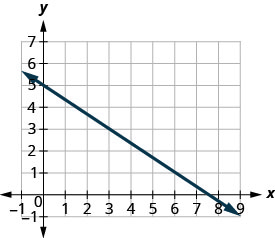
找到所示直线的斜率。
- 回答
-
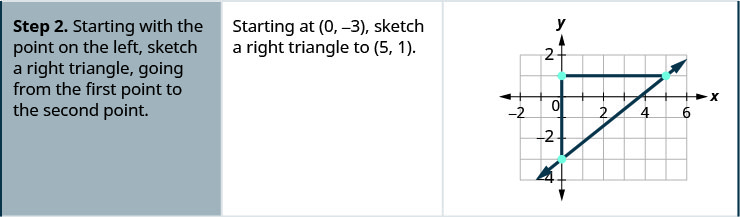
在图表上找到坐标为整数的两个点。 (0,5) 和 (3,3) 哪个点在左边? (0,5) 从 (0,5) 开始,画一个直角三角形到 (3,3)。 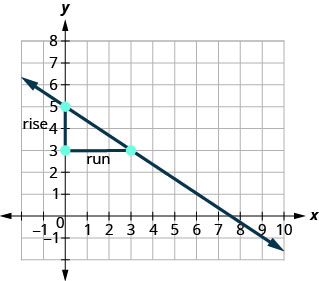
算上涨幅度——它是负数。 上升幅度为 −2。 计算跑步次数。 跑步是 3。 使用斜率公式。 \(m = \frac{\text{rise}}{\text{run}}\) 替换上升和运行的值。 \(m = \frac{-2}{3}\) 简化。 \(m = -\frac{2}{3}\) 直线的斜率为\(-\frac{2}{3}\)。 因此,当 xx 减少 2 个单位时 y 增加 3 个单位。
如果我们使用点 (−3,7) 和 (6,1) 来找出直线的斜率会怎样?
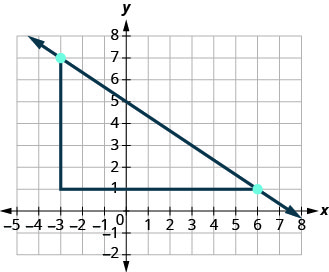
-
上升幅度将为 −6,运行将为 9。 然后\(m = \frac{-6}{9}\),这简化为\(m = -\frac{2}{3}\)。 请记住,使用哪个点并不重要,直线的斜率始终相同。
找到所示直线的斜率。
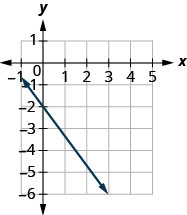
- 回答
-
\(-\frac{4}{3}\)
找到所示直线的斜率。
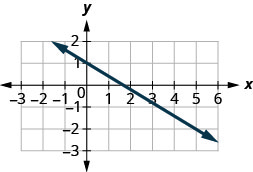
- 回答
-
\(-\frac{3}{5}\)
在最后两个示例中,直线有 y-intercept 和整数值,因此使用 y-intercept 作为找到斜率的点之一比较方便。 在下一个示例中,y 截距是一个分数。 我们将不使用该点,而是寻找坐标为整数的另外两个点。 这将使斜率计算变得更容易。
找到所示直线的斜率。

- 回答
-
在图表上找到坐标为整数的两个点。 (2,3) 和 (7,6) 哪个点在左边? (2,3) 从 (2,3) 开始,画一个直角三角形到 (7,6)。 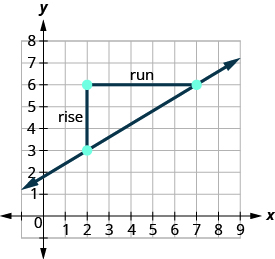
算上涨幅度。 上升幅度为 3. 计算跑步次数。 跑步是 5。 使用斜率公式。 \(m = \frac{\text{rise}}{\text{run}}\) 替换上升和运行的值。 \(m = \frac{3}{5}\) 直线的斜率为\(\frac{3}{5}\)。 这意味着当 x 增加 3 个单位时 y 增加 5 个单位。
当我们使用地理板来介绍斜率的概念时,我们说我们总是从左边的点开始,然后计算上升和跑步次数以到达右边的点。 这样,跑步总是正值,上升决定斜率是正还是负。
如果我们从右边的点开始,会发生什么?
让我们再次使用分数 (2,3) 和 (7,6),但现在我们将从 (7,6) 开始。
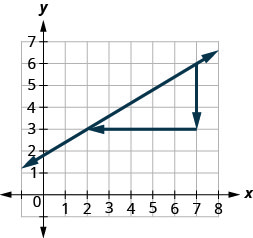
- \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
- 无论从哪里开始,直线的斜率总是相同的。
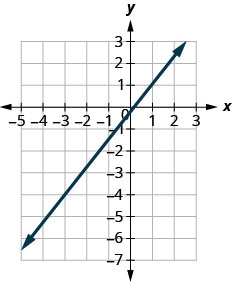
找到所示直线的斜率。
- 回答
-
\(\frac{5}{4}\)
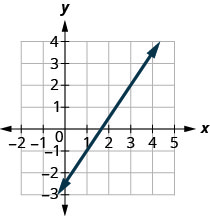
找到所示直线的斜率。
- 回答
-
\(\frac{3}{2}\)
找出水平线和垂直线的斜率
你还记得水平线和垂直线有什么特别之处吗? 他们的方程只有一个变量。
\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]
那么我们如何找到水平线 y=4y=4 的斜率呢? 一种方法是绘制水平线,在水平线上找到两个点,然后计算上升和跑步。 让我们看看当我们这样做时会发生什么。
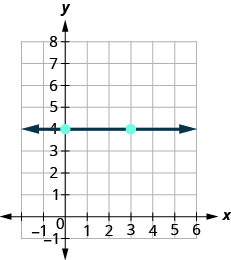
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)
所有水平线的斜率均为 0。 当 y 坐标相同时,上升为 0。
水平线 y=b 的斜率为 0。
你房间的地板是水平的。 它的斜率为 0。 如果你小心翼翼地将球放在地板上,它就不会滚开。
现在,我们来考虑一条垂直线,即直线。
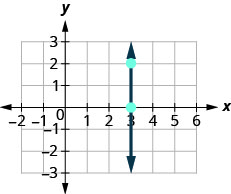
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)
但是我们不能除以 0。 未定义除以 0。 所以我们说垂直线 x=3x=3 的斜率是未定义的。
任何垂直线的斜率均未定义。 当直线的 x 坐标全部相同时,游程为 0。
垂直线 x=a 的斜率未定义。
找出每条线的斜率:
ⓐ x=8 ⓑ y=−5。
- 回答
-
ⓐ x=8
这是一条垂直线。
它的斜率未定义。
ⓑ y=−5
这是一条水平线。
它的斜率为 0。
找出直线的斜率:x=−4。
- 回答
-
未定义
找出直线的斜率:y=7。
- 回答
-
0
请记住,我们从左到右 “读” 一行,就像我们用英语阅读书面文字一样。
使用斜率公式求出两点间直线的斜率
进行操纵数学练习 “两点之间的线条斜率” 将有助于你更好地理解如何找到两点之间直线的斜率。有时候,当我们没有图表来计算上升和跑步时,我们需要找到两点之间直线的斜率。 我们可以在网格纸上绘制点,然后计算上升和跑步,但正如我们将看到的,有一种方法可以在不绘制图表的情况下找到斜率。 在开始之前,我们需要引入一些代数表示法。
我们已经看到,有序对 (x, y) 给出了点的坐标。 但是当我们处理斜坡时,我们使用两个点。 如何使用同一个符号(x,y)来表示两个不同的点? 数学家使用下标来区分点。
\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]
在数学中使用下标非常类似于小学时使用姓氏首字母缩写。 也许你还记得三年级的劳拉 C. 和 Laura M.
我们将使用\(\left(x_{1}, y_{1}\right)\)来识别第一个点和\(\left(x_{2}, y_{2}\right)\)识别第二个点。
如果我们有两个以上的分数,我们可以使用\(\left(x_{3}, y_{3}\right)\)\(\left(x_{4}, y_{4}\right)\)、等等。
让我们再看一下两点 (2,3) 和 (7,6) 之间的直线的斜率,看看上升和跑步与两点坐标的关系。
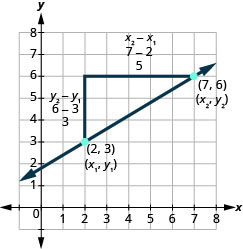
由于我们有两个点,我们将使用下标表示法\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\)。
在图表上,我们计算了 3 的上升和 5 的运行次数。
请注意,通过减去 y 坐标 6 和 3 可以得出 3 的上升。
\[3=6-3\]
通过减去 x 坐标 7 和 2 可以得到 5 的游程。
\[5 = 7 - 2\]
我们知道\(m = \frac{\text{rise}}{\text{run}}\)。 所以\(m = \frac{3}{5}\)。
我们重写上升并通过输入坐标来运行\(m = \frac{6-3}{7-2}\)
但是 6 是 y2,第二个点的 y 坐标,3 是 y1,第一个点的 y 坐标。
因此,我们可以使用下标表示法重写斜率。 \(m = \frac{y2-y1}{7-2}\)
另外,7 是 x2,第二个点的 x 坐标,2 是 x1,第一个点的 x 坐标。
因此,我们再次使用下标表示法重写斜率。 \(m = \frac{y2-y1}{x2-x1}\)
我们已经证明这实际上\(m = \frac{y2-y1}{x2-x1}\)是另一个版本\(m = \frac{\text{rise}}{\text{run}}\)。 当直线上有两个点时,我们可以使用这个公式来找出直线的斜率。
两点\(\left(x_{1}, y_{1}\right)\)和之间的直线的斜率\(\left(x_{2}, y_{2}\right)\)为
\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
这是斜率公式。
斜率是:
\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]
使用斜率公式求出点 (1,2) 和 (4,5) 之间直线的斜率。
- 回答
-
\(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)
让我们通过使用计算图表上的斜率来确认这一点\(m = \frac{\text{rise}}{\text{run}}\)。
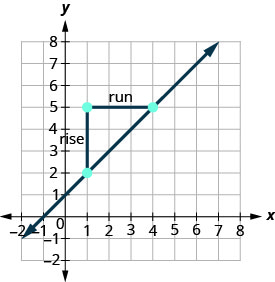
你称之为 point #1 和哪个点称之为 point #2 都没关系。 斜率将相同。 自己试试计算。
使用斜率公式求出穿过以下点的直线的斜率:(8,5) 和 (6,3)。
- 回答
-
1
使用斜率公式求出穿过以下点的直线的斜率:(1,5) 和 (5,9)。
- 回答
-
1
使用斜率公式求出穿过点 (−2、−3) 和 (−7,4) 的直线的斜率。
- 回答
-
\(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)
让我们在所示的图表上验证这个斜率。
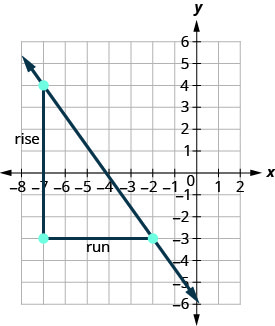
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]
使用斜率公式求出穿过以下点的直线的斜率:(−3,4) 和 (2, −1)。
- 回答
-
-1
使用斜率公式求出穿过一对点的直线的斜率:(−2,6) 和 (−3, −4)。
- 回答
-
10
给定一个点和斜率绘制一条直线
到目前为止,在本章中,我们已经通过绘制点、使用截距以及识别水平线和垂直线来绘制线条。
我们可以用来绘制线条的另一种方法叫做 p oint—slope 方法。 当我们知道一个点和直线的斜率时,我们将使用这种方法。 我们将从绘制点开始,然后使用斜率的定义来绘制直线图。
绘制穿过斜率为的点 (1, −1) 的直线图\(m = \frac{3}{4}\)。
- 回答
-




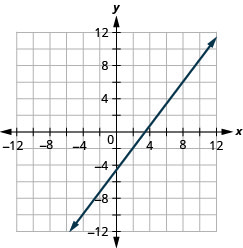
用斜率绘制穿过点 (2, −2) 的直线\(m = \frac{4}{3}\)。
- 回答
-
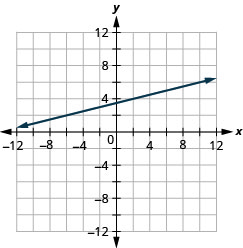
用斜率绘制穿过点 (−2,3) 的直线\(m=\frac{1}{4}\)。
- 回答
-
- 绘制给定点。
- 使用斜率公式\(m=\frac{\text { rise }}{\text { rise }}\)来确定上升和游程。
- 从给定点开始,计算上涨幅度,然后跑到第二个点。
- 用直线连接各点。
使用斜率为 y 的截距 2 绘制直线图\(m=−\frac{2}{3}\)。
- 回答
-
绘制给定点,即 y 截距 (0,2)。
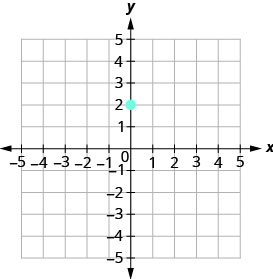
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)
计算上升和奔跑。 标记第二点。
-
用一条线将两点连接起来。
-
你可以通过找到第三点来检查你的工作。 既然斜率是\(m=−\frac{2}{3}\),它可以写成\(m=\frac{2}{-3}\)。 回到 (0,2) 并计算上升 2 和运行 −3。
使用 y 截距 4 和斜率绘制直线图\(m=−\frac{5}{2}\)。
- 回答
-
使用 x 截距 −3 和斜率绘制直线图\(m=−\frac{3}{4}\)。
- 回答
-
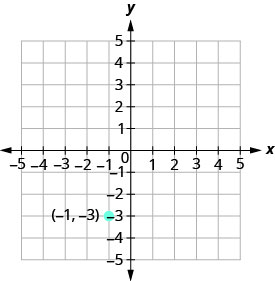
绘制穿过斜率为 m=4 的点 (−1, −3) 的直线。
- 回答
-
绘制给定点。
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)
计算上升幅度并跑步并标记第二个点。
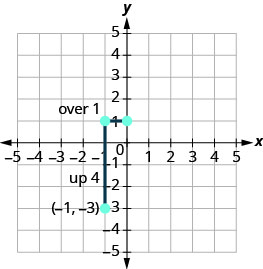
-
用一条线将两点连接起来。
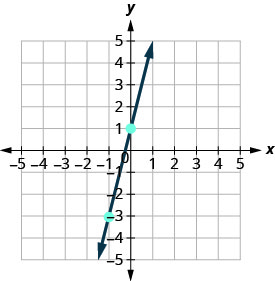
-
你可以通过找到第三点来检查你的工作。 由于斜率为 m=4,因此可以将其写成\(m = \frac{-4}{-1}\)。 回到 (−1, −3) 并计算上升 −4 和跑步 −1。
用点 (−2,1) 和斜率 m=3 绘制直线图。
- 回答
-
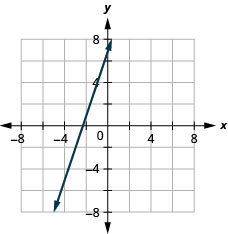
用点 (4, −2) 和斜率 m=−2 绘制直线图。
- 回答
-
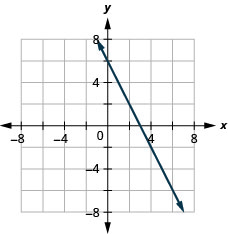
求解斜率应用程序
在本节的开头,我们说过斜率在现实世界中有许多应用。 现在让我们来看几个。
建筑物屋顶的 “间距” 是屋顶的坡度。 在有大雪的气候中,了解球场很重要。 如果屋顶过于平坦,积雪的重量可能会导致屋顶倒塌。 所示屋顶的坡度是多少?
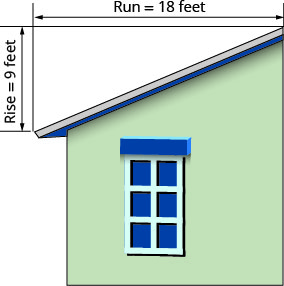
- 回答
-
\(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)
使用练习\(\PageIndex{40}\),用上升 = 14 代替 run = 24。
- 回答
-
\(\frac{7}{12}\)
使用练习\(\PageIndex{40}\),用上升 = 15 代替 run = 36。
- 回答
-
\(\frac{5}{12}\)
你有没有想过从你家到街道的污水管道? 它们必须每英尺向下倾斜一\(\frac{1}{4}\)英寸才能正常排水。 所需的斜率是多少?

- 回答
-
\(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)
每水平运行 48 英寸,管道就会下降 1 英寸。
找出每英尺向下倾斜一\(\frac{1}{3}\)英寸的管道的斜率。
- 回答
-
\(-\frac{1}{36}\)
找出每码向下倾斜一\(\frac{3}{4}\)英寸的管道的斜率。
- 回答
-
\(-\frac{1}{48}\)
访问这些在线资源以获取更多指导和练习,了解直线的斜率。
关键概念
- 使用以下方法从直线图中找到直线的斜率\(m=\frac{\text { rise }}{\text { run }}\)
- 在坐标为整数的直线上找到两个点。
- 从左边的点开始,画一个从第一个点到第二个点的右三角形。
- 计算三角形腿上的上升和跑步。
- 取上升与跑步的比率来找出斜率。
- 给定一个点和斜率绘制一条直线
- 绘制给定点。
- 使用斜率公式\(m=\frac{\text { rise }}{\text { run }}\)来确定上升和游程。
- 从给定点开始,计算上涨幅度,然后跑到第二个点。
- 用直线连接各点。
- 水平线的斜率
- 水平线 y=b 的斜率为 0。
- 垂直线的斜率
- 垂直线 x=a 的斜率未定义


