4.3：带截图的图表

学习目标

在本节结束时，您将能够：

• 识别图表上的 x 和 y 截距
• 从直线方程中找出 x 和 y 截距
• 使用截图绘制一条线

注意

在开始之前，请参加这个准备测验。

1. 解决：\(3\cdot 0+4y=−2\)。
   如果您错过了此问题，请查看练习 2.2.13。

识别图表上的 x 和 y 截距

每个线性方程都可以通过一条显示方程所有解的唯一线来表示。 我们已经看到，通过绘制点来绘制线条时，可以使用任意三种解决方案来绘制图形。 这意味着绘制线条的两个人可能会使用不同的三点集。

乍一看，它们的两条线可能看起来不一样，因为它们会标有不同的点。 但是，如果所有工作都正确完成，则线条应该完全相同。 识别它们确实是同一条线的一种方法是查看这条线与 x 轴和 y 轴交叉的位置。 这些点被称为直线的截点。

一条线的截取次数

直线与 x 轴和 y 轴交叉的点称为直线的截距。

让我们来看一下图中线条的图表\(\PageIndex{1}\)。

图\(\PageIndex{1}\)：横过 x 负轴的图形示例。

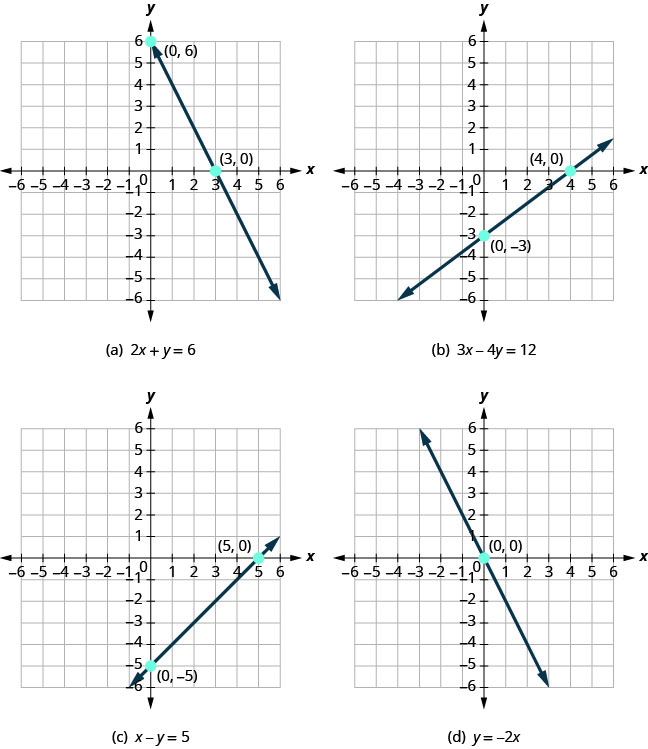
首先，注意每条线与 x 负轴交叉的位置。 参见图\(\PageIndex{1}\)。

桌子\(\PageIndex{1}\)

图	该直线在以下位置与 x 轴交叉：	订购了这个积分的配对
图 (a)	3	(3,0)
图 (b)	4	(4,0)
图 (c)	5	(5,0)
图 (d)	0	(0,0)

你看到图案了吗？

对于每一行，直线与 x 轴交叉的点的 y 坐标为零。 直线与 x 轴交叉的点的形式为 (a,0)，被称为直线的 x 截距。 当 y 为零时，会出现 x-截距。 现在，让我们看一下这些直线与 y 轴交叉的点。 参见表\(\PageIndex{2}\)。

桌子\(\PageIndex{2}\)

图	该直线在以下位置与 x 轴交叉：	订购了这个积分的配对
图 (a)	6	(0,6)
图 (b)	−3	(0, −3)
图 (c)	−5	(0,5)
图 (d)	0	(0,0)

这里的图案是什么？

在每行中，直线与 y 轴交叉点的 x-坐标为零。 直线与 y 轴交叉的点的形式为 (0, b)，称为直线的 y 截距。 当 x 为零时，会出现 y 截距。

直线的 X-截距和 Y-截距

x-截距是直线与 x 轴交叉的点 (a,0)。

y-截距是直线与 y 轴交叉的点 (0, b)。

图\(\PageIndex{2}\)

练习\(\PageIndex{1}\)

在每张图上找出 x 和 y 截距。

图\(\PageIndex{3}\)

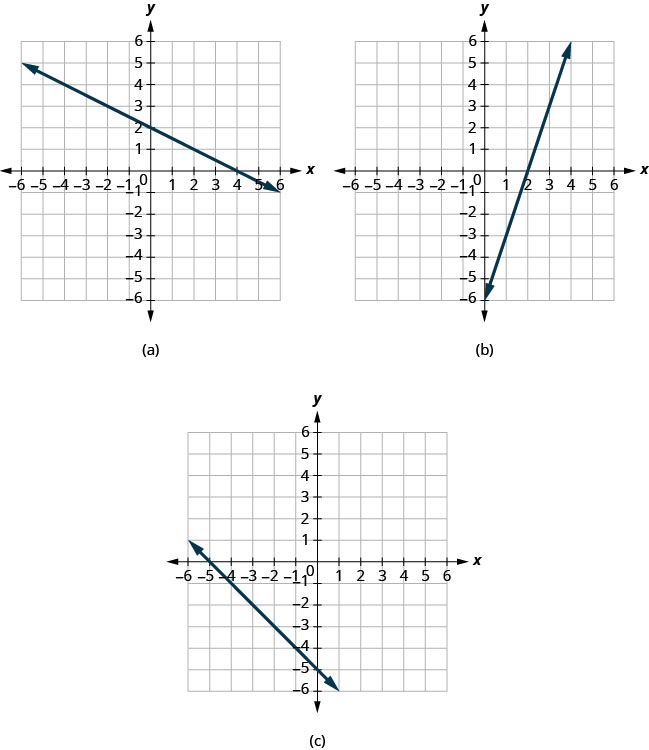
回答

(a) 图形在点 (4,0) 处穿过 x 轴。 x-截距为 (4,0)。
该图在点 (0,2) 处穿过 y 轴。 y 截距为 (0,2)。

(b) 图形在点 (2,0) 处穿过 x 轴。 x-截距为 (2,0)
图形在点 (0, −6) 处穿过 y 轴。 y 截距为 (0, −6)。

(c) 图形在点 (−5,0) 处穿过 x 轴。 x-截距为 (−5,0)。
该图在点 (0, −5) 处穿过 y 轴。 y 截距为 (0, −5)。

练习\(\PageIndex{2}\)

在图表上找出 x 和 y 截距。

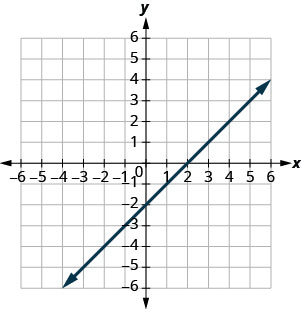
回答

x-截距:(2,0); y-截距:(0, −2)

练习\(\PageIndex{3}\)

在图表上找出 x 和 y 截距。

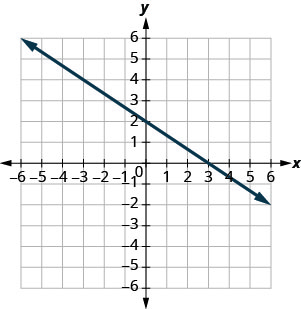
回答

x-截距：(3,0)，y-截距：(0,2)

从直线方程中找出 x-和 y-截距

认识到 x 截距在 y 为零时发生，y 截距在 x 为零时发生，这为我们提供了一种从直线的方程中求出直线的截距的方法。 要找出 x-截距，让 y=0 求解 x。 要找出 y 截距，让 x=0 求解 y。

X-和 Y-从直线方程中截取

使用直线方程。 要查找：

• x-直线的截距，让 y=0 求解 x。
• y-直线的截距，让 x=0 求解 y。

练习\(\PageIndex{4}\)

找出 2x+y=6 的截取次数。

回答

我们将让 y=0 找出 x-截距，让 x=0 找出 y 截距。 我们将填写表格，这使我们想起了我们需要找到的东西。

要找出 x-截距，假定 y=0。

桌子\(\PageIndex{3}\)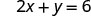

假设 y = 0。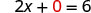
简化。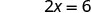
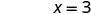
x 截距为	(3, 0)
要找出 y 截距，假设 x = 0。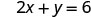
假设 x = 0。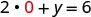
简化。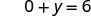
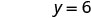
y 截距为	(0, 6)

截距是点 (3,0) 和 (0,6)，如表所示\(\PageIndex{4}\)。

桌子\(\PageIndex{4}\)

2x+y=6
x	y
3	0
0	6

练习\(\PageIndex{5}\)

找出 3x+y=12 的截取次数。

回答

x-截距：(4,0)，y-截距：(0,12)

练习\(\PageIndex{6}\)

找出 x+4y=8 的截取次数。

回答

x-截距：(8,0)，y-截距：(0,2)

练习\(\PageIndex{7}\)

找出 4x—3y=12 的截取次数。

回答

要找出 x 截距，假定 y = 0。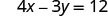
假设 y = 0。
简化。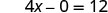
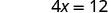
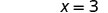
x 截距为	(3, 0)
要找出 y 截距，假设 x = 0。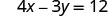
假设 x = 0。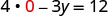
简化。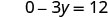
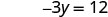
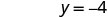
y 截距为	(0, −4)

桌子\(\PageIndex{5}\)

截距是点 (3, 0) 和 (0, −4)，如下表所示。

桌子\(\PageIndex{6}\)

4x−3y=12
x	y
3	0
0	−4

练习\(\PageIndex{8}\)

找出 3x—4y=12 的截取次数。

回答

x-截距：(4,0)，y-截距：(0, −3)

练习\(\PageIndex{9}\)

找出 2x—4y=8 的截取次数。

回答

x-截距：(4,0)，y-截距：(0, −2)

使用截图画一条线

要通过绘制点来绘制线性方程图，您需要找到三个坐标为方程解的点。 你可以使用 x 和 y 截距作为你的三个点中的两个。 找到拦截点，然后找到第三个点以确保准确性。 确保各点对齐，然后画出直线。 这种方法通常是绘制线条的最快方法。

练习\(\PageIndex{10}\): How to Graph a Line Using Intercepts

使用截取图表 —x+2y=6。

回答

练习\(\PageIndex{11}\)

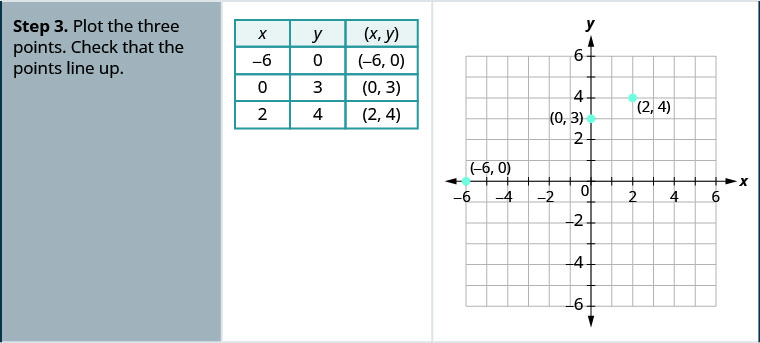
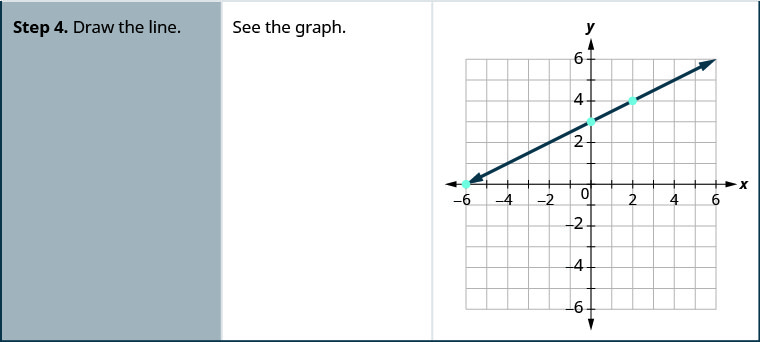
使用截图绘制 x—2y=4。

回答

练习\(\PageIndex{12}\)

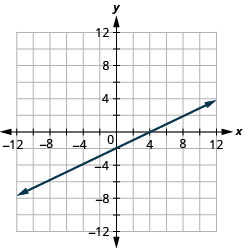
使用截取图表 —x+3y=6。

回答

使用截距绘制线性方程的步骤总结如下。

使用截距绘制线性方程图。

1. 找出直线的 x 和 y 截距。
   • 让 y=0 求解 x
   • 假设 x=0 然后求解 y。
2. 找到方程的第三个解。
3. 绘制这三个点并检查它们是否对齐。
4. 画出这条线。

练习\(\PageIndex{13}\)

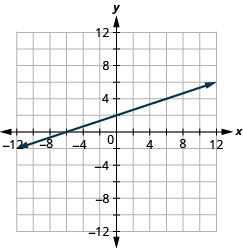
使用截取图表 4x—3y=12。

回答

找到拦截点和第三个点。

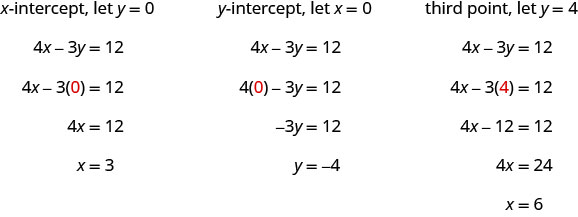
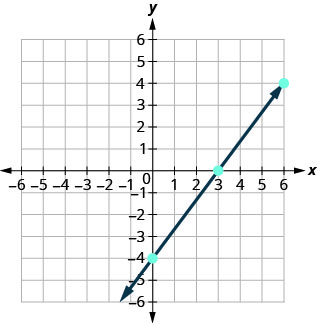
我们在表中列出了点\(\PageIndex{7}\)并显示了下图。

4x−3y=12
x	y	(x, y)
3	0	(3,0)
0	−4	(0, −4)
6	4	(6,4)

桌子\(\PageIndex{7}\)

练习\(\PageIndex{14}\)

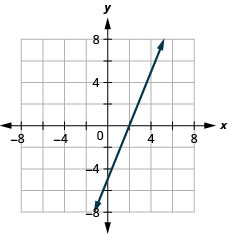
使用截取图表 5x—2y=10。

回答

练习\(\PageIndex{15}\)

使用截取图表 3x—4y=12。

回答

练习\(\PageIndex{16}\)

使用截图绘制 y=5x。

回答

这条线只有一个截距。 这是点 (0,0)。

为了确保准确性，我们需要绘制三个点。 由于 x-和 y-截距是同一个点，我们需要另外两个点来绘制直线。

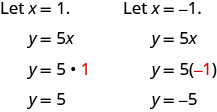
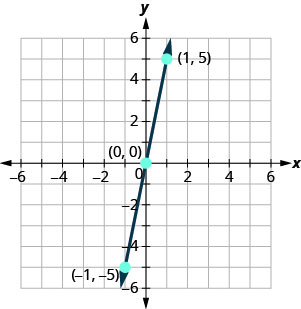
参见表\(\PageIndex{8}\)。

y=5x
x	y	(x, y)
		(0,0)
		(1,5)
−1	−5	(−1、−5)

桌子\(\PageIndex{8}\)

绘制这三个点，检查它们是否对齐，然后画出直线。

练习\(\PageIndex{17}\)

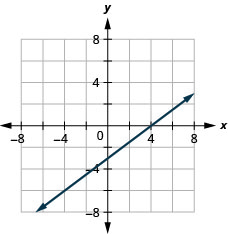
使用截图绘制 y=4x。

回答

练习\(\PageIndex{18}\)

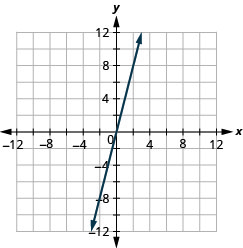
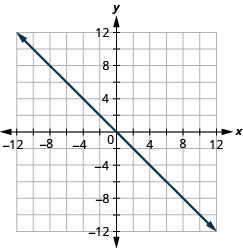
图 y=−x 截取次数。

回答

关键概念

• 从直线方程中找出 x-和 y-截距
  • 使用直线方程求出直线的 x 截距，让 y=0 求解 x。
  • 使用直线方程求出直线的 y 截距，让 x=0 求解 y。
• 使用截距绘制线性方程图
  1. 找出直线的 x 和 y 截距。
     假设 y=0 并求解 x。
     假设 x=0 然后求解 y。
  2. 找到方程的第三个解。
  3. 绘制这三个点，然后检查它们是否对齐。
  4. 画出这条线。
• 选择最便捷的绘制线条方法的策略：
  • 考虑方程的形式。
  • 如果它只有一个变量，则它是一条垂直线或水平线。
    x=a 是一条在 a
    y=b 处穿过 x 轴的垂直线，是一条在 b 处穿过 y 轴的水平线。
  • 如果 y 在方程的一侧是孤立的，则通过绘制点来绘制图形。
  • 为 x 选择任意三个值，然后求解相应的 y 值。
  • 如果方程的形式为 ax+by=c，则找出截距。 找到 x 和 y 截距，然后找出第三个点。

词汇表

直线的截取次数

直线与 x 轴和 y 轴交叉的点称为直线的截点。

x-截距

直线与 x 轴交叉的点 (a,0)；y 为零时出现 x 截距。

y-截距

直线与 y 轴交叉的点 (0, b)；当 x 为零时出现 y 截距。