4.2E:练习
- Page ID
- 204743
练习成就完美
认识方程解与其图之间的关系
在以下练习中,针对每个有序的对子决定:
- 有序对是方程的解吗?
- 点在直线上吗?
y=x+2
- (0,2)
- (1,2)
- (−1,1)
- (−3、−1)
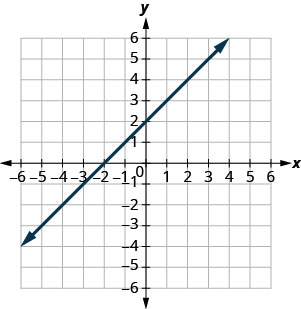
- 回答
-
- 是;不是
- 不;不
- 是的;是的
- 是的;是的
y=x−4
- (0, −4)
- (3, −1)
- (2,2)
- (1, −5)
\(y=\frac{1}{2} x-3\)
- (0, −3)
- (2, −2)
- (−2、−4)
- (4,1)
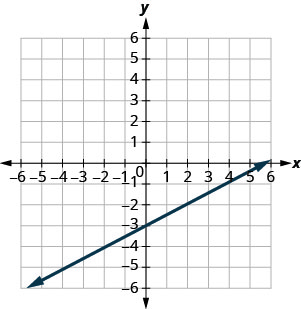
- 回答
-
- 是的;是的
- 是的;是的
- 是的;是的
- 不;不
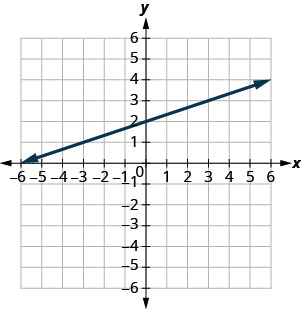
\(y=\frac{1}{3} x+2\)
- (0,2)
- (3,3)
- (−3,2)
- (−6,0)
通过绘制点来绘制线性方程图
在以下练习中,通过绘制点来绘制图形。
\(y=3 x-1\)
- 回答
-
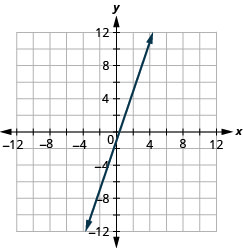
\(y=2 x+3\)
\(y=-2 x+2\)
- 回答
-
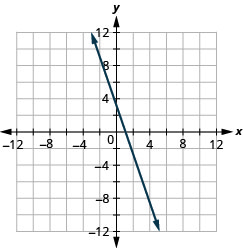
\(y=-3 x+1\)
\(y=x+2\)
- 回答
-
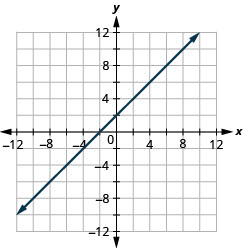
\(y=x-3\)
\(y=-x-3\)
- 回答
-
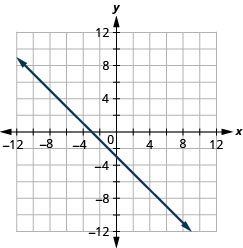
\(y=-x-2\)
\(y=2 x\)
- 回答
-
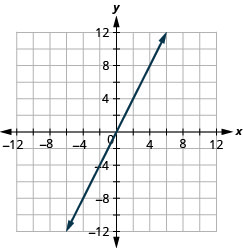
\(y=3 x\)
\(y=-4 x\)
- 回答
-
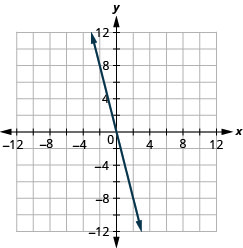
\(y=-2 x\)
\(y=\frac{1}{2} x+2\)
- 回答
-
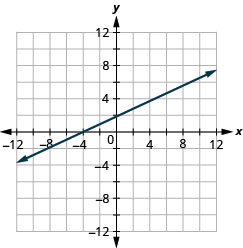
\(y=\frac{1}{3} x-1\)
\(y=\frac{4}{3} x-5\)
- 回答
-
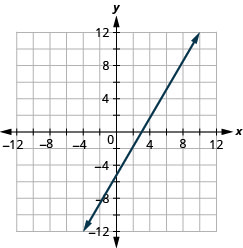
\(y=\frac{3}{2} x-3\)
\(y=-\frac{2}{5} x+1\)
- 回答
-
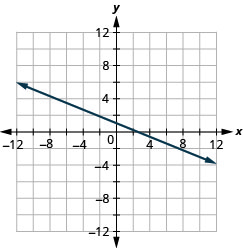
\(y=-\frac{4}{5} x-1\)
\(y=-\frac{3}{2} x+2\)
- 回答
-
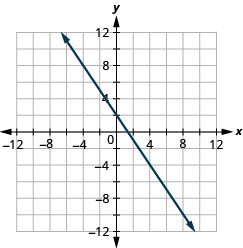
\(y=-\frac{5}{3} x+4\)
\(x+y=6\)
- 回答
-
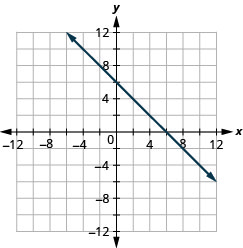
\(x+y=4\)
\(x+y=-3\)
- 回答
-
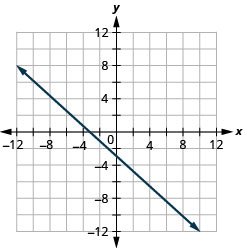
\(x+y=-2\)
\(x-y=2\)
- 回答
-
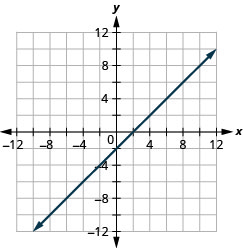
\(x-y=1\)
\(x-y=-1\)
- 回答
-
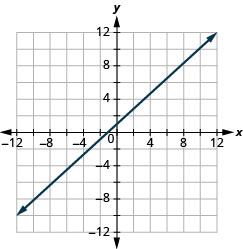
\(x-y=-3\)
\(3 x+y=7\)
- 回答
-
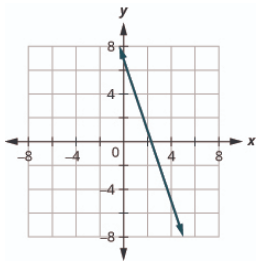
\(5x+y=6\)
2x+y=−3
- 回答
-
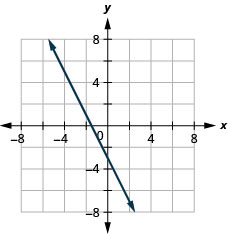
\(4x+y=−5\)
\(\frac{1}{3} x+y=2\)
- 回答
-
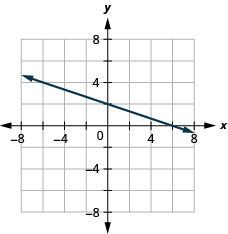
\(\frac{1}{2} x+y=3\)
\(\frac{2}{5} x-y=4\)
- 回答
-
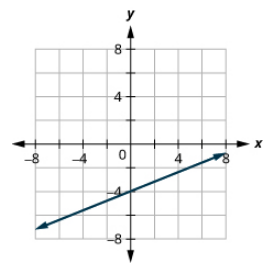
\(\frac{3}{4} x-y=6\)
\(2 x+3 y=12\)
- 回答
-
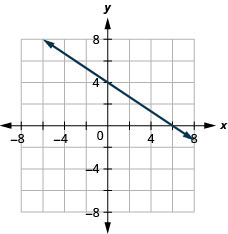
4x+2y=12
3x−4y=12
- 回答
-
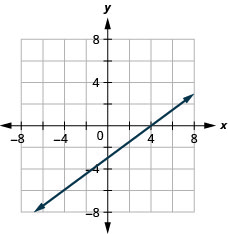
2x−5y=10
x−6y=3
- 回答
-
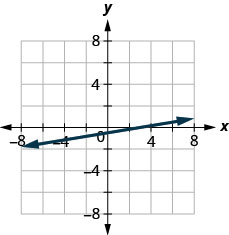
x−4y=2
5x+2y=4
- 回答
-
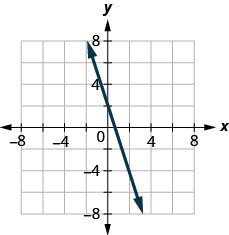
3x+5y=5
绘制垂直线和水平线
在以下练习中,绘制每个方程的图表。
x=4
- 回答
-
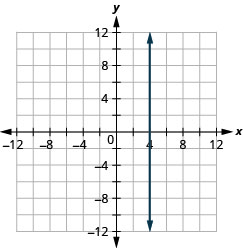
x=3
x=−2
- 回答
-
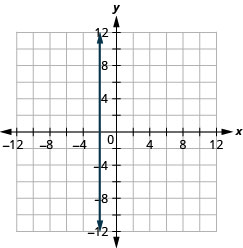
x=−5
y=3
- 回答
-
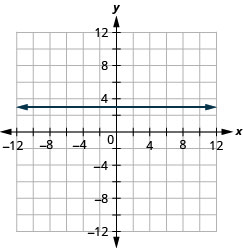
y=1
y=−5
- 回答
-
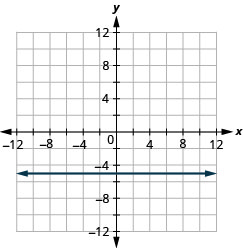
y=−2
\(x=\frac{7}{3}\)
- 回答
-
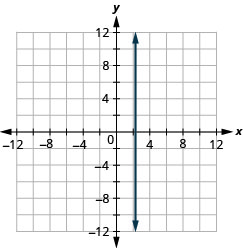
\(x=\frac{5}{4}\)
\(y=-\frac{15}{4}\)
- 回答
-
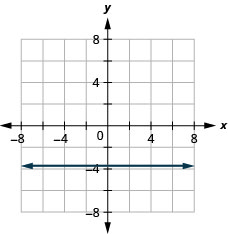
\(y=-\frac{5}{3}\)
在以下练习中,用相同的矩形坐标系绘制每对方程的图形。
y=2x 和 y=2
- 回答
-
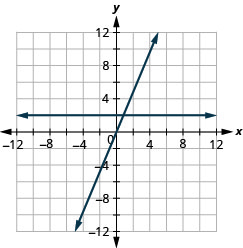
y=5x 和 y=5
\(y=-\frac{1}{2} x\)和\(y=-\frac{1}{2}\)
- 回答
-
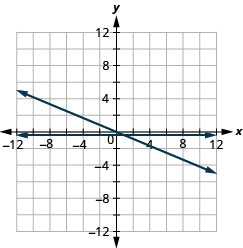
\(y=-\frac{1}{3} x\)和\(y=-\frac{1}{3}\)
混合练习
在以下练习中,绘制每个方程的图表。
y=4x
- 回答
-
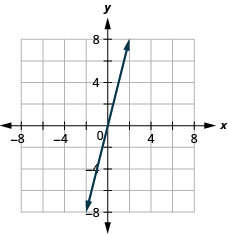
y=2x
\(y=-\frac{1}{2} x+3\)
- 回答
-
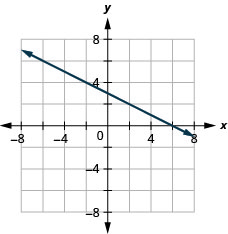
\(y=\frac{1}{4} x-2\)
y=−x
- 回答
-
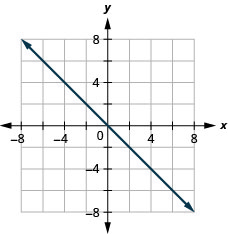
y=x
x−y=3
- 回答
-
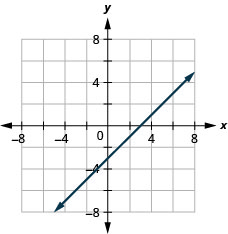
x+y=−5
4x+y=2
- 回答
-
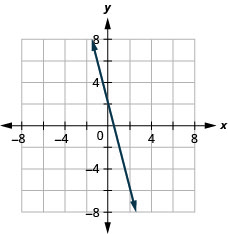
2x+y=6
y=−1
- 回答
-
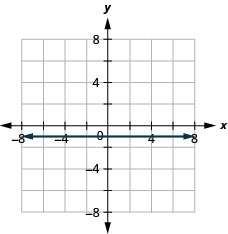
y=5
2x+6y=12
- 回答
-
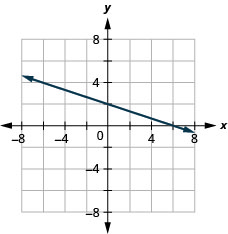
5x+2y=10
x=3
- 回答
-
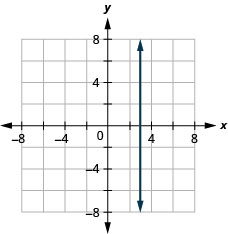
x=−4
日常数学
房车费用。 罗宾逊夫妇租了一个星期的房车去度假。 他们租房的费用为594美元加上每英里0.32美元,因此线性方程y=594+0.32x给出了行驶xx英里的成本。 计算行驶 400、800 和 1200 英里的租金成本,然后绘制线条图。
- 回答
-
722 美元、850 美元、978 美元
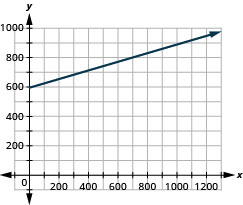
每周收益。 在他工作的美术馆里,萨尔瓦多每周获得200美元的报酬,外加他销售额的15%,所以等式y=200+0.15x给出了他卖出x美元艺术品的收入。 计算萨尔瓦多卖出 900 美元、1600 美元和 2000 美元的收入,然后绘制线条图。
写作练习
解释你将如何选择三个\(x\)值来制作一个表格来绘制线条图\(y=\frac{1}{5} x-2\)
- 回答
-
答案会有所不同。
垂直线和水平线的方程有什么区别?
自检
ⓐ 完成练习后,使用这份清单来评估你对本节目标的掌握程度。
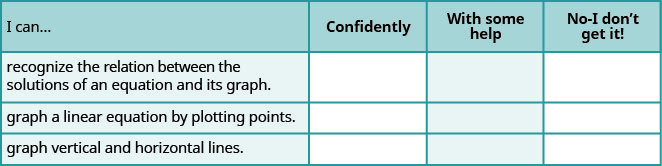
ⓑ 看完这份清单后,你会怎么做才能对所有目标充满信心?