4.2:在两个变量中绘制线性方程
- Page ID
- 204726
在本节结束时,您将能够:
- 认识方程解与其图形之间的关系。
- 通过绘制点来绘制线性方程图。
- 绘制垂直线和水平线。
认识方程解与其图之间的关系
在上一节中,我们找到了方程的几种解\(3x+2y=6\)。 它们列在表中\(\PageIndex{1}\)。 因此,有序对 (0,3)、(2,0) 和\((1,\frac{3}{2})\)是方程的一些解\(3x+2y=6\)。 我们可以在直角坐标系中绘制这些解,如图所示\(\PageIndex{1}\)。
| 3x+2y=6 | ||
| x | y | (x, y) |
| 0 | 3 | (0,3) |
| 2 | 0 | (2,0) |
| 1 | \(\frac{3}{2}\) | \((1, \frac{3}{2})\) |
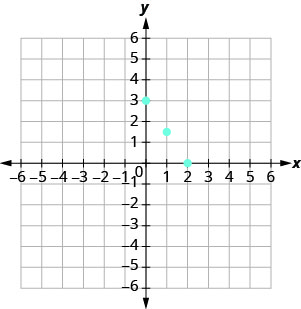
注意到积分是如何完美排列的了吗? 我们将这些点用一条线连接起来,得到方程 3x+2y=6 的图形。 参见图\(\PageIndex{2}\)。 注意直线两端的箭头。 这些箭头表示直线继续。
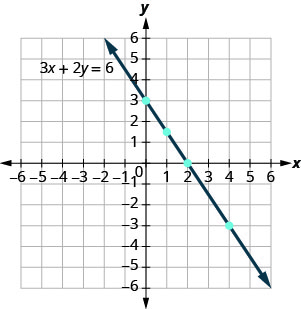
直线上的每个点都是方程的解。 此外,这个方程的每个解都是这条线上的一个点。 不在线上的点不是解决方案。
请注意,坐标为 (−2,6) 的点位于图中所示的直线上\(\PageIndex{3}\)。 如果你在方程中替换 x=−2 和 y=6,你会发现它是方程的解。
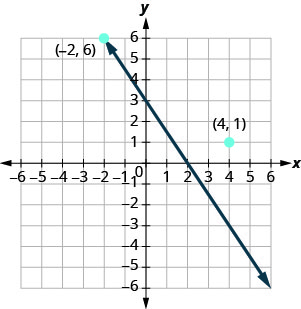
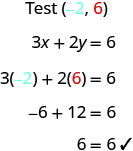
因此,点 (−2,6) 是方程的解\(3x+2y=6\)。 (短语 “坐标为 (−2,6) 的点” 通常缩写为 “点 (−2,6)”。)
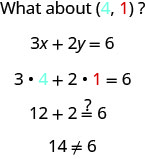
线性方程 Ax+By=C 的图形是一条直线。
- 直线上的每个点都是方程的解。
- 这个方程的每个解都是这条线上的一个点。
显示了 y=2x−3 的图形。
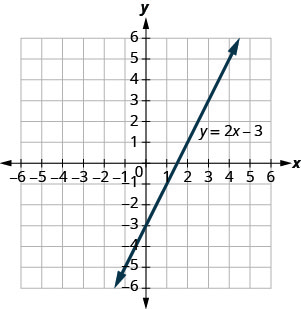
对于每对订购的配对,请决定:
- 有序对是方程的解吗?
- 点在直线上吗?
A (0, −3) B (3,3) C (2, −3) D (−1, −5)
- 回答
-
将 x 和 y 值替换到方程中,以检查有序对是否是方程的解。
- 1。
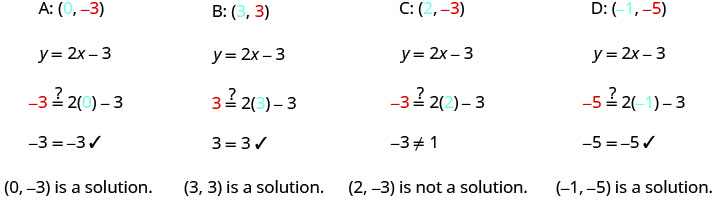
- 2。 绘制点 A (0,3)、B (3,3)、C (2、−3) 和 D (−1、−5)。
-
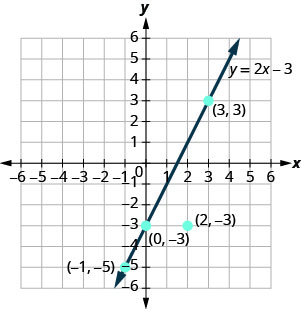
y=2x−3 解的点在线上,但不是解的点不在线上。
点 (0,3)、(3,3) 和 (−1, −5) 在 y=2x−3 线上,点 (2, −3) 不在线上。
使用 y=3x−1 的图形来确定每个有序对是否为:
- 方程的解。
- 上线了。
- (0, −1)
- (2,5)
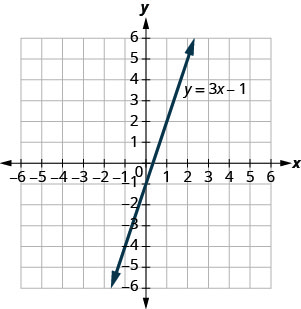
- 回答
-
- 是的,是的
- 是的,是的
使用 y=3x−1 的图形来确定每个有序对是否为:
- 方程的解
- 上线了
- (3, −1)
- (−1、−4)
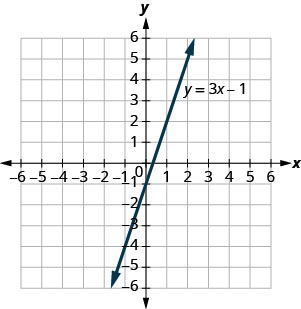
- 回答
-
- 不,不
- 是的,是的
通过绘制点来绘制线性方程图
有几种方法可用于绘制线性方程。 我们用来绘制 3x+2y=6 图表的方法称为绘制点或点绘法。
通过绘制点来绘制方程 y=2x+1 的图形。
- 回答
-
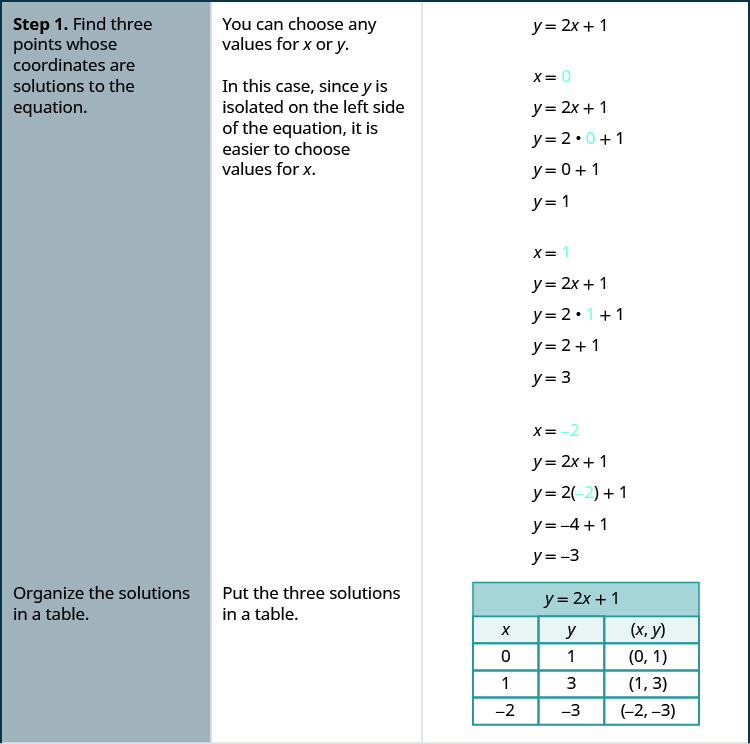
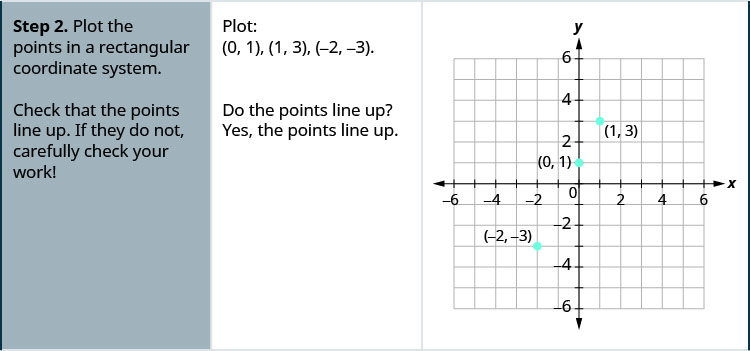
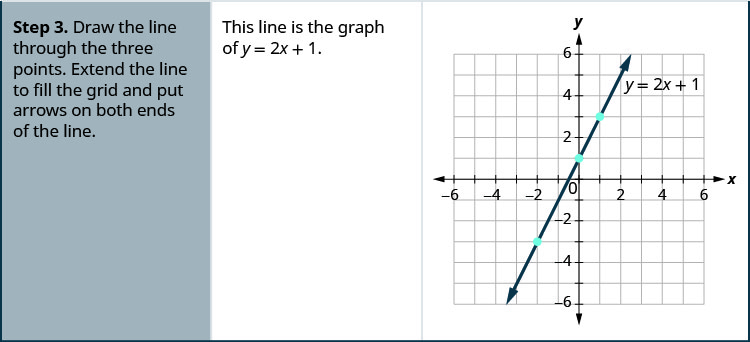
通过绘制点来绘制方程图:y=2x−3。
- 回答
-
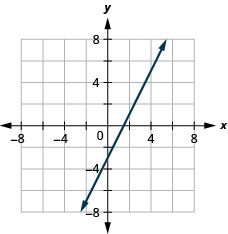
通过绘制点来绘制方程图:y=−2x+4。
- 回答
-
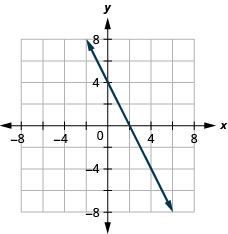
下面总结了通过绘制点来绘制线性方程时要采取的步骤。
- 找出坐标为方程解的三个点。 将它们整理在桌子里。
- 在矩形坐标系中绘制点。 检查各点是否对齐。 如果没有,请仔细检查你的工作。
- 画一条穿过这三个点的直线。 延伸线条以填充网格,并在直线的两端放置箭头。
的确,确定一条线只需要两个点,但是使用三个点是个好习惯。 如果你只绘制两个点而其中一个点不正确,你仍然可以画一条线,但它不能代表方程的解。 这将是错误的路线。
如果您使用三个积分,而一个点不正确,则这些点将不会排成一列。 这告诉你出了点问题,你需要检查一下你的工作。 请看图 (a) 和 (b) 部分之间的区别\(\PageIndex{4}\)。

让我们再举一个例子。 这次,我们将在一个网格上显示最后两个步骤。
绘制方程 y=−3x 的图表。
- 回答
-
找出作为方程解的三个点。 在这里,再说一遍,为 x 选择值比较容易。你明白原因了吗?
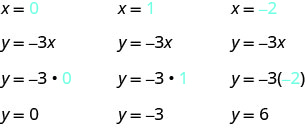
-
我们在表中列出了分数\(\PageIndex{2}\)。
桌子\(\PageIndex{2}\) y=−3x x y (x, y) 0 0 (0,0) 1 −3 (1, −3) −2 6 (−2,6) 绘制点图,检查它们是否对齐,然后画出直线。
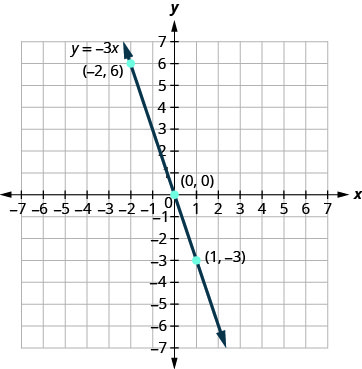
通过绘制点来绘制方程图:y=−4x。
- 回答
-
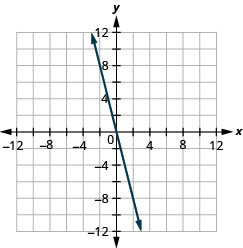
通过绘制点来绘制方程图:y=x。
- 回答
-

当方程包含分数作为 x 系数时,我们仍然可以用任何数字代替 x。但是,如果我们为 x 的值做出 “好” 的选择,则数学会更容易。这样我们就可以避免分数答案,因为分数答案很难精确绘制出来。
绘制方程图\(y = \frac{1}{2}x + 3\)。
- 回答
-
找出作为方程解的三个点。 由于该方程将分数\(\frac{1}{2}\)作为 x 的系数,因此我们将谨慎选择 x 的值。 我们将使用零作为一个选项,使用2的倍数作为其他选项。 为什么 2 的倍数是 x 值的好选择?
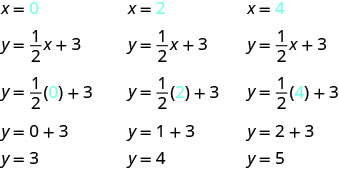
-
积分如表所示\(\PageIndex{3}\)。
桌子\(\PageIndex{3}\) y=12x+3 x y (x, y) 0 3 (0,3) 2 4 (2,4) 4 5 (4,5) -
绘制点图,检查它们是否对齐,然后画出直线。
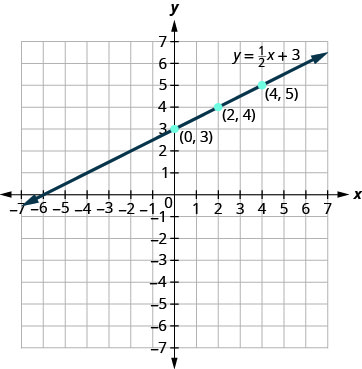
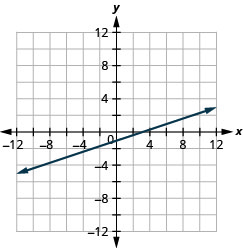
绘制方程图\(y = \frac{1}{3}x - 1\)。
- 回答
-
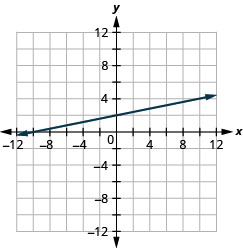
绘制方程图\(y = \frac{1}{4}x + 2\)。
- 回答
-
到目前为止,我们绘制的所有方程都以 x 给出 y。现在我们将绘制一个 x 和 y 在同一侧的方程。 让我们看看方程式 2x+y=3 中会发生什么。 如果 y=0 x 的值是多少?
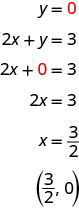
这个点有 x 坐标的分数,虽然我们可以绘制这个点的图形,但很难精确地绘制分数。 请记住,在示例 y=12x+3 中,我们仔细选择了 x 的值,以免绘制分数的图形。 如果我们求解 y 的方程 2x+y=3,则更容易找到该方程的三个解。
\[\begin{aligned} 2 x+y &=3 \\ y &=-2 x+3 \end{aligned}\]
表中显示了 x=0、x=1 和 x=−1 的解\(\PageIndex{4}\)。 该图如图所示\(\PageIndex{5}\)。
| 2x+y=3 | ||
| x | y | (x, y) |
| 0 | 3 | (0,3) |
| 1 | 1 | (1,1) |
| −1−1 | 5 | (−1,5) |
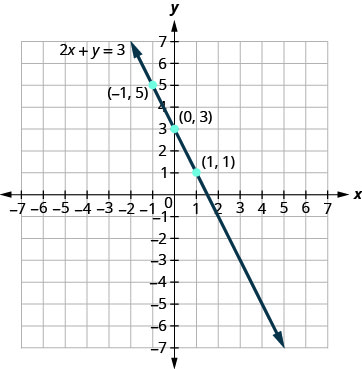
你能在直线\((\frac{3}{2}, 0)\)上让 y=0 找到我们找到的点吗?
绘制方程 3x+y=−1。
- 回答
-
\(\begin{array}{lrll} { \text { Find three points that are solutions to the equation. } } & {3 x+y} &{=} &{-1} \\ {\text { First solve the equation for } y.} &{y} &{=} &{-3 x-1} \end{array}\)
我们将 x 设为 0、1 和 −1 来找出 3 个点。 表中显示了已排序的货币对\(\PageIndex{5}\)。 绘制点图,检查它们是否对齐,然后画出直线。 参见图\(\PageIndex{6}\)。
桌子\(\PageIndex{5}\) 3x+y=−1 x y (x, y) 0 −1 (0, −1) 1 −4 (1, −4) −1 2 (−1,2) -
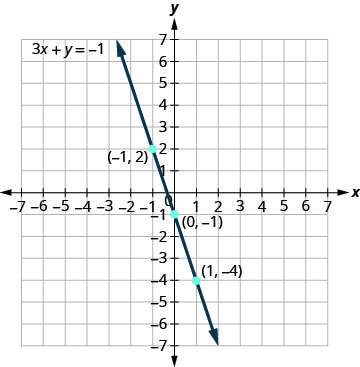
图\(\PageIndex{6}\)
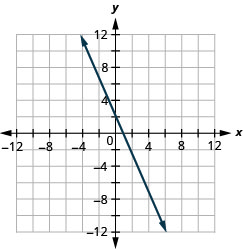
绘制方程式 2x+y=2。
- 回答
-
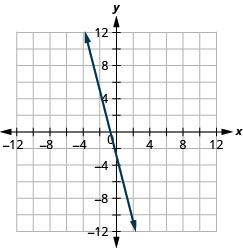
绘制方程 4x+y=−3。
- 回答
-
如果你能选择任意三个点来绘制一条线,你怎么知道你的图表是否与书中答案中显示的图表相匹配? 如果图形交叉 x 轴和 y 轴的点相同,则图表匹配!
练习\(\PageIndex{13}\)中的方程以标准形式编写,x 和 y 在同一边。 我们仅用一个步骤就求解了 y 的方程。 但是对于其他标准形式的方程,求解 y 并不容易,因此我们将把它们保留为标准形式。 我们仍然可以通过让 x=0 求解 y 来找到要绘制的第一个点。我们可以通过让 y=0 然后求解 x 来绘制第二个点。然后我们将使用其他值为 x 或 y 绘制第三个点。
绘制方程图\(2x−3y=6\)。
- 回答
-
\(\begin{array}{lrll} \text { Find three points that are solutions to the } & 2 x-3 y &= &6 \\ \text { equation. } & 2 x-3 y&=&6 \\ \text { First let } x=0 . & 2(0)-3 y&=&6 \\ \text { Solve for } y . &-3 y&=&6 \\ & y&=&-2 \\\\ \text { Now let } y=0 . & 2 x-3(0)&=&6 \\ \text { Solve for } x . & 2 x&=&6 \\ & x&=& 3 \\ \\ \text{ We need a third point. Remember, we can}&2(6)-3 y &=&6 \\ \text{ choose any value for x or y. We’ll let x = 6.}&12-3 y &=&6 \\ \text{ Solve fory.}&-3 y &=&-6 \\ &y &=&2\end{array}\)
我们在表中列出了有序的对\(\PageIndex{6}\)。 绘制点图,检查它们是否对齐,然后画出直线。 参见图\(\PageIndex{7}\)。
桌子\(\PageIndex{6}\) 2x−3y=6 x 是的 (x, y) 0 −2 (0, −2) 3 0 (3,0) 6 2 (6,2) 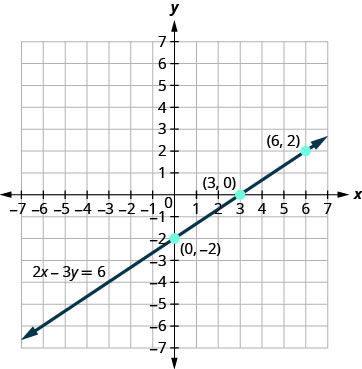
图\(\PageIndex{7}\)
绘制方程图\(4x+2y=8\)。
- 回答
-
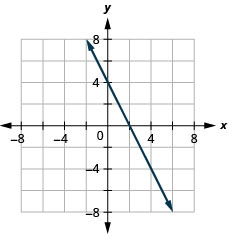
绘制方程图\(2x−4y=8\)。
- 回答
-
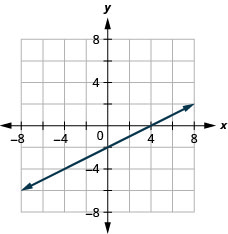
绘制垂直线和水平线
我们可以用一个变量绘制一个方程吗? 只有 x 而不是 y,还是只有 y 没有 x? 我们将如何制作一个值表来绘制点数?
让我们考虑方程 x=−3。 该方程只有一个变量 x。该方程表示 x 始终等于 −3,因此其值不取决于 y。不管 y 是什么,x 的值始终为 −3。
因此,要创建一个值表,请为所有 x 值输入 −3。 然后为 y 选择任意值。由于 x 不依赖于 y,所以你可以选择任何你喜欢的数字。 但是为了拟合坐标图上的点,我们将使用 1、2 和 3 作为 y 坐标。 见表\(\PageIndex{7}\)
| x=−3 | ||
|---|---|---|
| x | y | (x, y) |
| −3 | 1 | (−3,1) |
| −3 | 2 | (−3,2) |
| −3 | 3 | (−3,3) |
绘制表中的点\(\PageIndex{7}\)并用直线将它们连接起来。 请注意,在图中\(\PageIndex{8}\),我们已经绘制了一条垂直线。
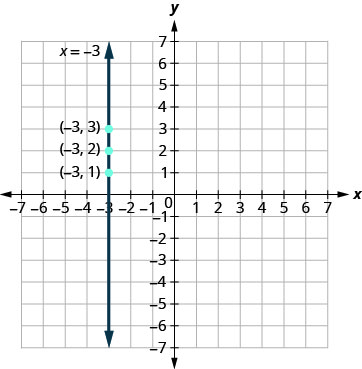
垂直线是形式为 x=a 的方程的图形。
直线在 (a,0) 处穿过 x 轴。
绘制方程 x=2 的图表。
- 回答
-
方程只有一个变量 x,而 x 始终等于 2。 我们创建表,\(\PageIndex{8}\)其中 x 始终为 2,然后为 y 输入任何值。图形是一条在 2 处穿过 x 轴的垂直线。 参见图\(\PageIndex{9}\)。
桌子\(\PageIndex{8}\) x=2 x y (x, y) 2 1 (2,1) 2 2 (2,2) 2 3 (2,3) -
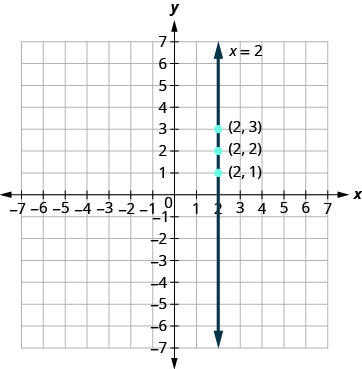
图\(\PageIndex{9}\)
绘制方程 x=5 的图表。
- 回答
-
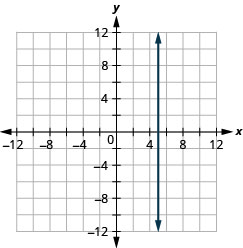
绘制方程 x=−2 的图表。
- 回答
-
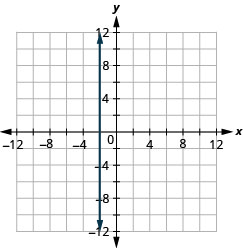
如果方程有 y 但没有 x 怎么办? 让我们绘制方程 y=4。 这次 y-v alue 是一个常数,所以在这个方程中,y 不依赖于 xx。 为表中的所有 y 填入 4,\(\PageIndex{9}\)然后为 x 选择任意值。我们将使用 0、2 和 4 作为 x 坐标。
| y=4 | ||
| x | y | (x, y) |
| 0 | 4 | (0,4) |
| 2 | 4 | (2,4) |
| 4 | 4 | (4,4) |
该图是一条在 4 处穿过 y 轴的水平线。 参见图\(\PageIndex{10}\)。
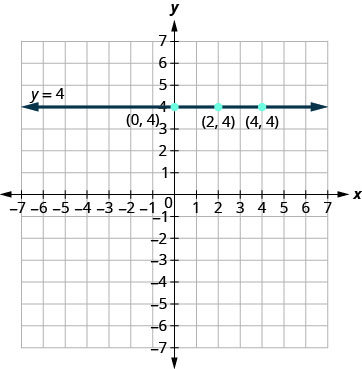
水平线是形式为 y=b 的方程的图形。
直线在 (0, b) 处穿过 y 轴。
绘制方程 y=−1 的图表。
- 回答
-
方程 y=−1y=−1 只有一个变量 y。y 的值是恒定的。 表中所有有序对都\(\PageIndex{10}\)具有相同的 y 坐标。 该图是一条在 −1−1 处穿过 y 轴的水平线,如图所示\(\PageIndex{11}\)。
桌子\(\PageIndex{10}\) y=−1 x y (x, y) Ta−1 (0, −1) −1 (3, −1) −3 −1 (−3、−1) 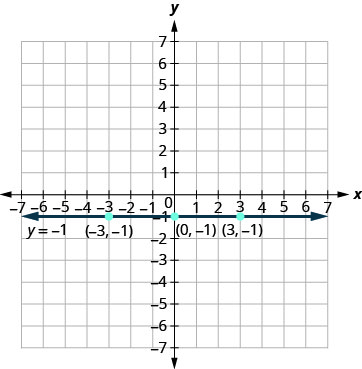
- 图\(\PageIndex{11}\)
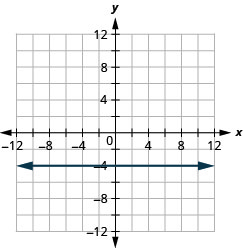
绘制方程 y=−4 的图表。
- 回答
-
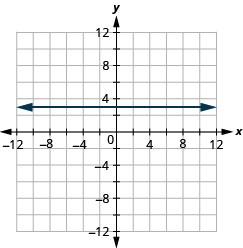
绘制方程 y=3 的图表。
- 回答
-
垂直线和水平线的方程看起来与像 y=4x 这样的方程非常相似。 方程 y=4x 和 y=4 有什么区别?
方程 y=4x 同时有 x 和 y。y 的值取决于 x 的值。y 坐标根据 x 的值而变化。方程 y=4 只有一个变量。 y 的值是恒定的。 y 坐标始终为 4。 它不依赖于 x 的值。参见表\(\PageIndex{11}\)。
| y=4x | y=4 | |||||
| x | y | (x, y) | x | y | (x, y) | |
| 0 | 0 | (0,0) | 0 | 4 | (0,4) | |
| 1 | 4 | (1,4) | 1 | 4 | (1,4) | |
| 2 | 8 | (2,8) | 2 | 4 | (2,4) | |
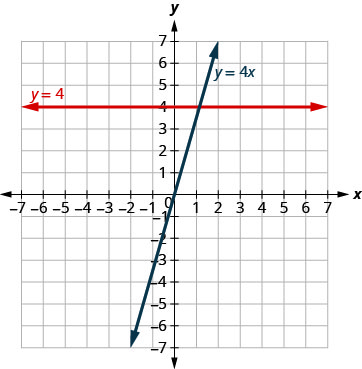
注意,在图中\(\PageIndex{12}\),方程 y=4x 给出了一条倾斜的线,而 y=4 给出了一条水平线。
在同一个直角坐标系中绘制图形 y=−3x 和 y=−3。
- 回答
-
请注意,第一个方程具有变量 x,而第二个方程没有。 见表\(\PageIndex{12}\)。 这两张图如图所示\(\PageIndex{13}\)。
桌子\(\PageIndex{12}\) y=−3x y=−3 x y (x, y) x y (x, y) (0,0) −3 (0, −3) −3 (1, −3) −3 (1, −3) −6 (2, −6) −3 (2, −3) 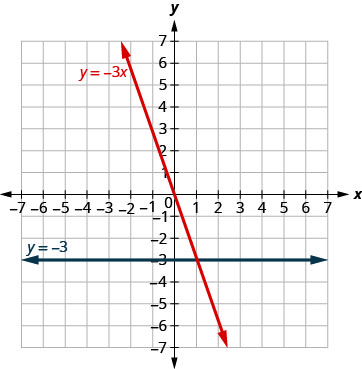
- 图\(\PageIndex{13}\)
在同一个直角坐标系中绘制图形 y=−4x 和 y=−4。
- 回答
-
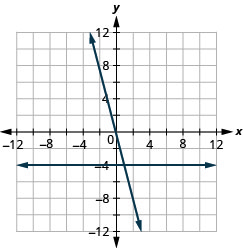
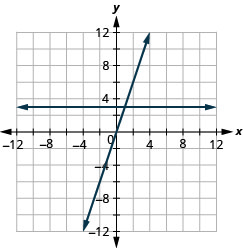
在同一个直角坐标系中绘制图形 y=3 和 y=3x。
- 回答
-
关键概念
- 通过绘制点来绘制线性方程图
- 找出坐标为方程解的三个点。 将它们整理在桌子里。
- 在矩形坐标系中绘制点。 检查各点是否对齐。 如果他们没有,请仔细检查你的作品!
- 画一条穿过这三个点的直线。 延伸线条以填充网格,并在直线的两端放置箭头。
词汇表
- 线性方程的图形
- 线性方程 Ax+By=C 的图形是一条直线。 直线上的每个点都是方程的解。 这个方程的每个解都是这条线上的一个点。
- 水平线
- 水平线是 y=b 形式的方程的图形。该直线在 (0, b) 处穿过 y 轴。
- 垂直线
- 垂直线是形式为 x=a 的方程的图形。该直线在 (a,0) 处穿过 x 轴。


