3.5:解决均匀运动应用程序
- Page ID
- 204833
在本节结束时,您将能够:
- 解决均匀运动应用程序
解决均匀运动应用程序
在计划公路旅行时,了解到达目的地需要多长时间或每天要走多远通常会有所帮助。 我们将使用距离、速率和时间公式 d=rt,我们已经看过了。
在本节中,我们将在比前面看到的需要多一点代数才能求解的情况中使用这个公式。 通常,我们将研究比较两种情况,例如两辆车以不同的速率或相反的方向行驶。 当每辆车的速度恒定时,我们称之为诸如均匀运动之类的应用程序。
我们的问题解决策略在这里仍然适用,但我们将增加第一步。 第一步将包括绘制一张示意图,显示示例中发生的情况。 绘制图表可以帮助我们了解正在发生的事情,这样我们就可以写出一个合适的方程式。 然后,我们将制作一张表格来整理信息,就像我们在资金申请中所做的那样。
此处列出了这些步骤以便于参考:
- 阅读问题。 确保所有文字和想法都被理解。
- 画一张图来说明发生了什么。
- 创建一个表来组织信息。
- 标注速率、时间、距离列。
- 列出两个场景。
- 写下你知道的信息。
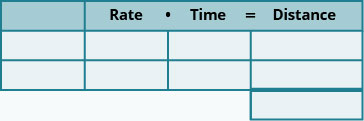
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 完成图表。
- 使用变量表达式表示每行中的该数量。
- 将速率乘以时间得出距离。
- 翻译成方程式。
- 用一句话用所有重要信息重述问题。
- 然后,将句子翻译成方程式。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
特快列车和当地列车离开匹兹堡前往华盛顿特区。特快列车可以在 4 小时内出行,而当地列车需要 5 个小时。 特快列车的速度比当地列车的速度快12英里/小时。 找出两列火车的速度。
- 回答
-
第 1 步。 阅读问题。 确保所有文字和想法都被理解。
画一张图来说明发生了什么。 下图是示例中发生的事情的草图。
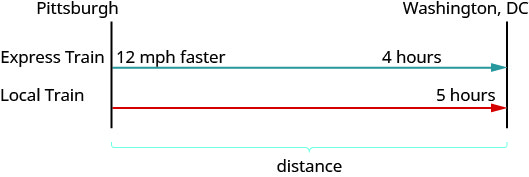
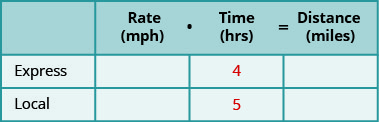
创建一个表来组织信息。 将列标记为 “速率”、“时间” 和 “距离”。 列出两个场景。 写下你知道的信息。
第 2 步。 确定我们在寻找什么。
我们被要求找出两列火车的速度。 请注意,距离公式使用 “rate” 一词,但是当我们在日常英语中谈论车辆时,更常见的是使用 “速度”。
第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。
完成图表使用变量表达式表示每行中的数量。 我们正在寻找火车的速度。 让我们让 r 表示当地列车的速度。 由于特快列车的速度快了 12 英里/小时,因此我们将其表示为 r+12。
\[\begin{aligned} r &=\text { speed of the local train } \\ r+12 &=\text { speed of the express train } \end{aligned}\]
在图表中填写速度。
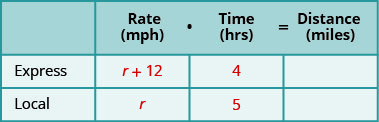
-
将速率乘以时间得出距离。
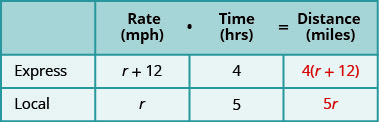
第 4 步。 翻译成方程式。
用一句话用所有重要信息重述问题。 然后,将句子翻译成方程式。 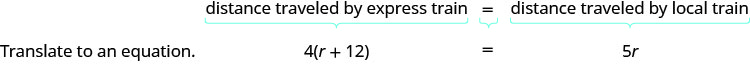
-
- 对这种情况进行建模的方程将来自距离之间的关系。 看看我们上面画的图。 特快列车的行驶距离与当地列车行驶的距离有何关系?
- 由于两列火车都从匹兹堡出发,前往华盛顿特区,因此它们的行驶距离相同。 所以我们这样写:
第 5 步。 使用良好的代数技巧求解方程。
第 6 步。 检查问题中的答案并确保答案合理。 \[\begin{array}{ll}{\text { express train }} & {60 \mathrm{mph}(4 \text { hours })=240 \mathrm{miles}} \\ {\text { local train }} & {48 \mathrm{mph}(5 \text { hours })=240 \mathrm{miles} \checkmark \end{array}\]现在求解这个方程。 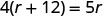
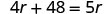
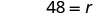
因此,当地列车的速度为48英里/小时。
查找特快列车的速度。 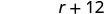


特快列车的速度为 60 英里/小时。
第 7 步。 用完整的句子回答问题。
当地列车的速度为48英里/小时,特快列车的速度为60英里/小时。
韦恩和丹尼斯喜欢骑自行车从河滨公园到海滩。 丹尼斯的速度比韦恩的速度快七英里/小时,因此 Wayne 骑车到海滩需要 2 个小时,而丹尼斯则需要 1.5 个小时才能骑行。 找出两个骑自行车的人的速度。
- 回答
-
Wayne 21 英里/小时,丹尼斯 28 英
杰罗米可以在4.5小时内从他在克利夫兰的家中开车到他在芝加哥的大学。 他妈妈要花6个小时才能开同样的车。 杰罗米每小时的行驶速度比他母亲快 20 英里。 找出杰罗米的速度和他母亲的速度。
- 回答
-
Jeromy 80 mph,妈妈 60 英里/小时
在最后一个例子的 “练习\(\PageIndex{4}\)” 中,我们有两列火车以相同的距离行驶。 图表和图表帮助我们编写了求解的方程式。 让我们看看在另一个案例中这是如何工作的。
克里斯托弗和他的父母相隔115英里。 他们在家中的一家餐馆见面,庆祝他母亲的生日。 克里斯托弗开了 1.5 个小时,而他的父母开了 1 个小时去餐厅。 克里斯托弗的平均时速比他父母的平均速度快10英里/小时。 克里斯托弗和他的父母开车去餐厅时的平均速度是多少?
- 回答
-
第 1 步。 阅读问题。 确保所有文字和想法都被理解。
画一张图来说明发生了什么。 下面显示了示例中正在发生的事情的草图。
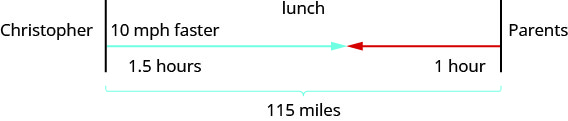
创建一个表来组织信息。
标注速率、时间、距离列。
列出两个场景。
写下你知道的信息。
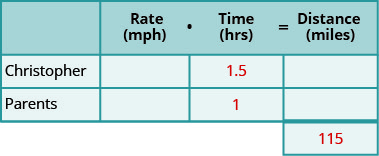
第 2 步。 确定我们在寻找什么。
我们被要求找出克里斯托弗和他父母的平均速度。
第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。
完成图表。 - 使用变量表达式表示每行中的该数量。
- 我们正在寻找他们的平均速度。 让我们让 r 表示父母的平均速度。 由于克里斯托弗的速度快了 10 英里/小时,我们将其表示为 r+10。
-
在图表中填写速度。
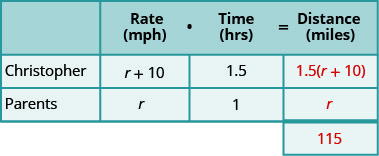
将速率乘以时间得出距离。
第 4 步。 翻译成方程式。
用一句话用所有重要信息重述问题。 然后,将句子翻译成方程式。 同样,我们需要确定距离之间的关系才能写出方程。 看看我们在上面创建的图表,注意克里斯托弗走过的距离和他父母旅行的距离之间的关系。克里斯托弗旅行的距离加上他父母的旅行距离加起来必须达到 115 英里。 所以我们这样写:

第 5 步。 使用良好的代数技巧求解方程。
\(\begin{array} {cc} {} &{1.5(r + 10) + r = 115} \\ {} &{1.5r + 15 + r = 115} \\ {\text{Now solve this equation.}} &{2.5r + 15 = 115} \\{} &{2.5r = 100} \\{} &{r = 40} \\ {} &{\text{so the parents' speed was 40 mph.}} \\ {} &{r + 10} \\ {\text{Christopher's speed is r + 10}} &{40 + 10} \\ {} &{50} \\ {} &{\text{Christopher's speed was 50 mph.}} \\ {} &{} \end{array}\)
第 6 步。 检查问题中的答案并确保答案合理。
\(\begin{array}{llll} {\text{Christopher drove}} &{50\text{ mph (1.5 hours)}} &{=} &{75\text{ miles}}\\ {\text{His parents drove}} &{40\text{ mph (1 hour)}} &{=} &{\underline{40 \text{ miles}}}\\ {} &{} &{} &{115\text{ miles}} \end{array}\)
\(\begin{array}{ll} {\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{} \\{} &{\text{Christopher's speed was 50 mph.}}\\ {} &{\text{His parents' speed was 40 mph.}} \end{array}\)
在她哥哥从伯克利开车去阿纳海姆的同一天,Carina正从阿纳海姆的家中开车去伯克利,所以他们决定沿途在Buttonwillow见面吃午饭。 从阿纳海姆到伯克利的距离为 410 英里。 Carina 花了 3 个小时才到达 Buttonwillow,而她的兄弟开车 4 个小时才能到达。 Carina 兄弟的平均行驶速度比 Carina 的平均时速快 15 英里/小时。 找出 Carina 和她兄弟的平均速度。
- 回答
-
Carina 50 mph,兄弟 65 英里/小时
阿什利在明尼阿波利斯上大学,距离她在苏福尔斯的家234英里。 她希望父母给她带更多的冬装,所以他们决定在明尼阿波利斯和苏福尔斯之间的路上的一家餐馆见面。 Ashley 和她的父母都开车两个小时去了餐厅。 Ashley 的平均速度比她父母的平均速度快七英里/小时。 找出阿什利和她父母的平均速度。
- 回答
-
父母 55 英里/小时,Ashley 62
在阅读下一个示例时,请考虑行驶距离的关系。 前两个例子中哪一个更类似于这种情况?
两名卡车司机同时离开州际公路上的休息区。 一辆卡车向东行驶,另一辆向西行驶。 向西行驶的卡车以 70 英里/小时的速度行驶,向东行驶的卡车的平均时速为 60 英里/小时。 它们在相隔 325 英里之前要行驶多久?
- 回答
-
第 1 步。 阅读问题。 确保所有文字和想法都被理解。
画一张图来说明发生了什么。
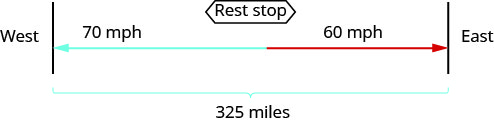
创建一个表来组织信息。

第 2 步。 确定我们在寻找什么。
我们被要求找出卡车在相距 325 英里之前行驶的时间。
第 3 步。 说出我们要找的东西。 选择一个变量来表示该数量。
我们正在寻找时光流逝。 两辆卡车的行驶时间相同。 让我们称时间为 t。 由于它们的速度不同,它们将行驶不同的距离。 完成图表。
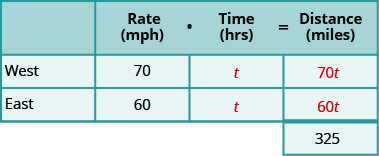
第 4 步。 翻译成方程式。
我们需要找到距离之间的关系才能写出方程。 从图中可以看出,每辆卡车的行驶距离之间有什么关系? 卡车向西行驶的距离加上卡车向东行驶的距离加起来必须为 325 英里。 所以我们这样写:

第 5 步。 使用良好的代数技巧求解方程。
\[\begin{array} {lrll} {\text{Now solve this equation. }} & {70 t+60 t} &{=} &{325} \\ {} &{130 t} &{=} &{325} \\ {} &{t} &{=} &{2.5} \end{array}\]
第 6 步。 检查问题中的答案并确保答案合理。
\(\begin{array}{llll} {\text{Truck going West}} &{70\text{ mph (2.5 hours)}} &{=} &{175\text{ miles}}\\ {\text{Truck going East}} &{60\text{ mph (2.5 hour)}} &{=} &{\underline{150 \text{ miles}}}\\ {} &{} &{} &{325\text{ miles}} \end{array}\)
\(\begin{array}{ll} \\{\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{\text{It will take the truck 2.5 hours to be 325 miles apart.}} \end{array}\)
皮埃尔和莫妮克同时离开了他们在波特兰的家。 皮埃尔在收费公路上以每小时 75 英里的速度向北行驶,而莫妮克则以每小时 68 英里的速度向南行驶。 他们相隔 429 英里需要多长时间?
- 回答
-
3 个小时
Thanh 和 Nhat 同时离开了他们在萨克拉曼多的办公室。 Thanh 在 5 号州际公路上以每小时 72 英里的速度向北行驶。 Nhat 在 I-5 上以每小时 76 英里的速度向南行驶。 他们相距 330 英里需要多长时间?
- 回答
-
2.2 小时
当我们使用距离速率和时间公式时,确保单位匹配非常重要。 例如,如果费率以英里/小时为单位,则时间必须以小时为单位。
当凯蒂·梅走路去学校时,她需要30分钟。 如果她骑自行车,则需要 15 分钟。 她骑自行车时的速度比走路时快三英里/小时。 她的步行速度和骑自行车的速度是多少?
- 回答
-
首先,我们绘制一张代表情况的图表,以帮助我们了解正在发生的事情。
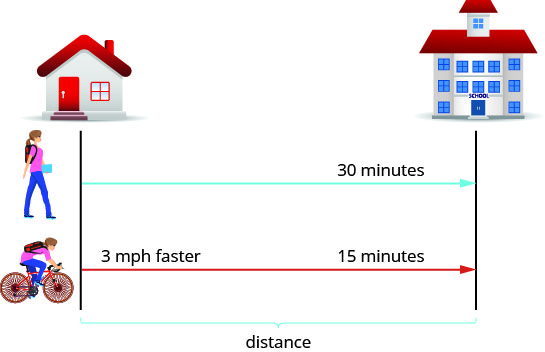
-
我们被要求找到她的速度行走和骑自行车。 让我们称她为步行速度 r。 由于她的骑行速度快了三英里/小时,因此我们将该速度称为r+3。 我们在图表中写下速度。
速度以英里/小时为单位,因此我们也需要用小时表示时间,以使单位相同。 请记住,一小时等于 60 分钟。 所以:
\[\begin{array}{l}{30 \text { minutes is } \frac{30}{60} \text { or } \frac{1}{2} \text { hour }} \\ {15 \text { minutes is } \frac{15}{60} \text { or } \frac{1}{4} \text { hour }}\end{array}\]
接下来,我们将速率乘以时间来填充距离列。
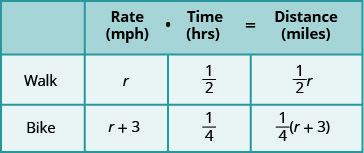
这个方程式将来自这样一个事实,即无论凯蒂·梅(Katie Mae)是步行还是骑自行车,她从家到学校的距离都是一样的。
所以我们说:

翻译成方程式。 
求解这个方程。 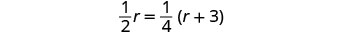
通过将方程中所有分数乘以 LCD 来清除分数。 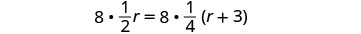
简化。 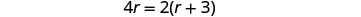
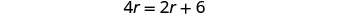


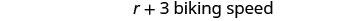

6 英里/小时
(凯蒂Mae 的骑行速度)让我们来看看这是否奏效。
步行 3 英里/小时(0.5 小时)= 1.5 英里
自行车 6 英里/小时(0.25 小时)= 1.5 英里是的,无论哪种方式,凯蒂·梅都要走1.5英里去学校。 凯蒂·梅的步行速度为 3 英里/小时。
她骑自行车的速度为 6 英里/小时。
Suzy 从停车场徒步上坡到瞭望塔需要 50 分钟。 她花了 30 分钟才徒步回到停车场。 她下坡的速度比上坡速度快1.2英里/小时。 查找 Suzy 的上坡和下坡速度。
- 回答
-
上坡 1.8 英里/小时,下坡 3 英里/小时
Llewyn 花了 45 分钟将他的船从码头向上游开到他最喜欢的钓鱼点。 他花了 30 分钟才把船开回下游到码头。 这艘船向下游行驶的速度比向上游行驶的速度快四英里/小时。 查找船的上游和下游速度。
- 回答
-
上游 8 英里/小时,下游 12 英里/小时
在距离、速率和时间公式中,时间代表实际经过的时间量(以小时、分钟等为单位)。 如果问题将开始和结束时间作为时钟时间,则我们必须找到经过的时间才能使用公式。
汉密尔顿喜欢去拉斯维加斯旅游,距离他在奥兰治县的家255英里。 在他最后一次旅行中,他在下午 2 点离开了家。 他旅行的第一部分是在拥挤的城市高速公路上。 下午 4:00,交通畅通无阻,他能够以比在拥挤区域开车时快 1.75 倍的速度穿越沙漠。 他在下午 6:30 抵达拉斯维加斯。 他在行程的每个环节都开了多快?
- 回答
-
图表将帮助我们模拟这次旅行。
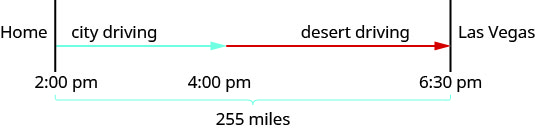
接下来,我们创建一个表来组织信息。
我们知道总距离为 255 英里。 我们正在寻找行程中每个部分的速度速度。 沙漠中的速度是城市速度的1.75倍。 如果我们让 r= 城市中的速率,那么沙漠中的速率为 1.75r。
这里的时间以时钟时间给出。 汉密尔顿在下午 2 点从家出发,下午 4:30 进入沙漠。 因此,他花了两个小时在城市拥挤的高速公路上行驶。 然后他从下午 4:00 到下午 6:30 在沙漠中开得更快。 所以他在沙漠里开了2.5个小时。
现在,我们将费率乘以乘以。
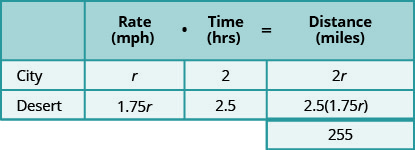
通过查看下图,我们可以看出,在城市中行驶的距离和在沙漠中行驶的距离之和为 255 英里。
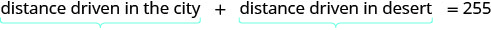
翻译成方程式。 
求解这个方程。 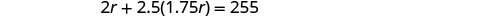
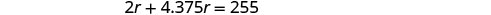
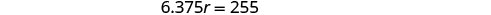
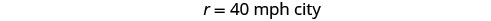
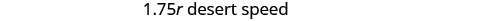
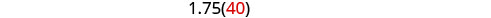
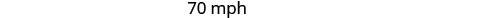
查看。

汉密尔顿在城市中行驶 40 英里/小时,在沙漠中行驶 70 英里/小时。
克鲁兹正在训练参加铁人三项比赛。 他在 6:00 离开家,一直跑到 7:30。 然后他骑自行车直到 9:45。 他总共行驶了 51 英里。 他骑自行车时的速度是跑步时速度的1.6倍。 查找 Cruz 的骑行和跑步速度。
- 回答
-
骑行 16 英里/小时,跑步 10 英里/小时
Phuong 在 10:00 骑自行车离开了家。 他在平坦的街道上骑车直到 11:15,然后上坡直到 11:45。 他总共骑了 31 英里。 他在平坦的街道上骑行速度是他在平坦街道上速度的0.6倍。 在平坦的街道上找到他的速骑自行车。
- 回答
-
上坡 12 英里/小时,平坦的街道 20 英里/小时
关键概念
- 距离、速率和时间
- D = r t 其中 D = 距离,r = 速率,t = 时间
- 问题解决策略——距离、速率和时间应用
- 阅读问题。 确保所有文字和想法都被理解。
画一张图来说明发生了什么。
创建表来整理信息:标注速率、时间、距离列。 列出两个场景。 写下你知道的信息。 - 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
完成图表。
使用变量表达式表示每行中的该数量。
将速率乘以时间得出距离。 - 翻译成方程式。
用一句话用所有重要信息重述问题。
然后,将句子翻译成方程式。 - 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
- 阅读问题。 确保所有文字和想法都被理解。


