3.4: 三角形、矩形和毕达哥拉斯定理
- Page ID
- 204850
在本节结束时,您将能够:
- 使用三角形的属性求解应用程序
- 使用毕达哥拉斯定理
- 使用矩形属性求解应用程序
使用三角形的属性求解应用程序
在本节中,我们将使用一些常见的几何公式。 我们将调整我们的问题解决策略,以便我们可以解决几何应用程序。 几何公式将命名变量并给出要解的方程。 此外,由于这些应用程序都将涉及某种形状,因此大多数人发现绘制图形并用给定信息对其进行标记会很有帮助。 我们将在几何应用问题解决策略的第一步中包括这一点。
- 阅读问题并确保所有文字和想法都被理解。 画出图形并用给定的信息贴上标签。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 标记它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查答案,将其替换回步骤 5 中求解的方程式中,并确保答案在问题的背景下有意义。
- 用完整的句子@@ 回答问题。
我们将通过查看三角形的属性来启动几何应用程序。 让我们回顾一下关于三角形的一些基本事实。 三角形有三个边和三个内角。 通常,每边都用小写字母标记,以匹配对面顶点的大写字母。
顶点一词的复数是顶点。 所有三角形都有三个顶点。 三角形由其顶点命名:图中的三角形\(\PageIndex{1}\)叫做\(\triangle{ABC}\)。
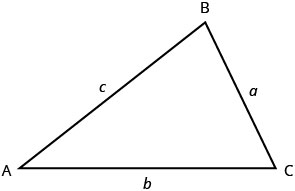
三角形的三个角度以特殊的方式相互关联。 他们的衡量标准总和是\(180^{\circ}\)。 请注意,我们读\(m\angle{A}\)作 “角度 A 的测量” 所以在图\(\triangle{ABC}\)中\(\PageIndex{1}\)。
\[m \angle A+m \angle B+m \angle C=180^{\circ} \nonumber\]
因为图的周长是其边界的长度,所以的周长\(\triangle{ABC}\)是其三边长度的总和。
\[P = a + b + c \nonumber\]
要找到三角形的面积,我们需要知道它的底部和高度。 高度是一条将底部连接到相反顶点并与底部成\(90^\circ\)角度的线。 我们将\(\triangle{ABC}\)再次绘制,现在显示高度\(h\)。 参见图\(\PageIndex{2}\)。
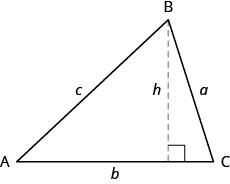
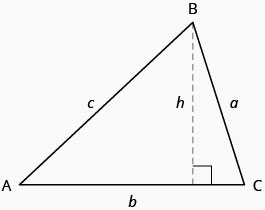
对于\(\triangle{ABC}\)
角度测量:
\[m \angle A+m \angle B+m \angle C=180^{\circ}\]
- 三角形角度的测量总和为 180°。
周长:
\[P = a + b + c\]
- 周长是三角形边长度的总和。
区域:
\(A = \frac{1}{2}bh, b = \text{ base }, h = \text{ height }\)
- 三角形的面积是基数乘以高度的一半。
三角形两个角度的测量值分别为 55 度和 82 度。 找到第三个角度的测量值。
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 | 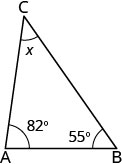 |
| 第 2 步。 确定你在找什么。 | 三角形中第三个角度的度量 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 让我们\(x=\)来测量角度。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式并替代。 | \(m \angle A+m \angle B+m \angle C=180^{\circ}\) |
| 第 5 步。 求解方程。 | \(\begin{array} {rll} {55 + 82 + x} &{=} &{180} \\ {137 + x} &{=} &{180} \\ {x} &{=} &{43} \end{array}\) |
| 第 6 步。 查看。 \(\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 第三个角度的测量值为 43 度。 |
三角形两个角度的测量值分别为 31 度和 128 度。 找到第三个角度的测量值。
- 回答
-
21 度
三角形两个角度的测量值分别为 49 度和 75 度。 找到第三个角度的测量值。
- 回答
-
56 度
三角花园的周长为 24 英尺。 两边的长度为四英尺零九英尺。 第三面有多长?
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 | 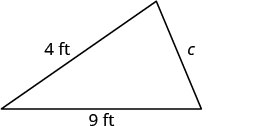  |
| 第 2 步。 确定你在找什么。 | 三角形第三边的长度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 让\(c=\)第三面。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式并替代。 | 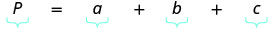 |
| 在给定的信息中替换。 | 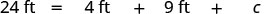 |
| 第 5 步。 求解方程。 |   |
| 第 6 步。 查看。 \(\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11} \\ {24} &{=} &{24\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 第三面长 11 英尺。 |
三角花园的周长为 48 英尺。 两边的长度分别为 18 英尺和 22 英尺。 第三面有多长?
- 回答
-
8 英尺
三角窗两边的长度为七英尺零五英尺。 周长为 18 英尺。 第三面有多长?
- 回答
-
6 英尺
三角形教堂窗户的面积为 90 平方米。 窗户的底部是 15 米。 窗户的高度是多少?
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 | 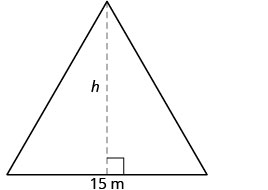 \(\text{ Area } = 90m^{2}\) |
| 第 2 步。 确定你在找什么。 | 三角形的高度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 让\(h=\)高度。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 |  |
| 在给定的信息中替换。 |  |
| 第 5 步。 求解方程。 | \(90 = \dfrac{15}{2}h\) \(12 = h\) |
| 第 6 步。 查看。 \(\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 三角形的高度为 12 米。 |
三角画的面积为 126 平方英寸。 底座为 18 英寸。 身高是多少?
- 回答
-
14 英寸
三角形帐篷门的面积为 15 平方英尺。 高度为五英尺。 基础是什么?
- 回答
-
6 英尺
我们到目前为止使用的三角形属性适用于所有三角形。 现在我们来看一种特定类型的三角形——直角三角形。 直角三角形有一个 90° 的角度,我们通常在角落里用一个小方块来标记。
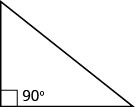
直角三角形有一个 90° 角,顶点处通常用正方形标记。
直角三角形的一个角度为 28°。 第三个角度的度量是多少?
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 | 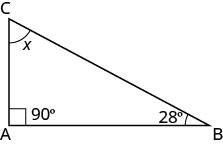 |
| 第 2 步。 确定你在找什么。 | 角度的测量 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 让我们\(x=\)来测量一个角度。 |
| 第 4 步。 翻译。 | \(m\angle{A} + m\angle{B} + m\angle{C} = 180\) |
| 写出相应的公式并替代。 | \(x+90+28=180\) |
| 第 5 步。 求解方程。 | \(x=62\) |
| 第 6 步。 查看。 \(\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 第三个角度的测量值为 62 °。 |
直角三角形的一个角度为 56°。 另一个小角度的度量是多少?
- 回答
-
34°
直角三角形的一个角度为 45°。 另一个小角度的度量是多少?
- 回答
-
45°
在我们到目前为止看到的例子中,我们可以画一个图形并在阅读问题后直接给它贴上标签。 在下一个例子中,我们必须用另一个角度来定义一个角度。 我们将等待绘制图形,直到我们为要寻找的所有角度写出表达式为止。
直角三角形的一个角度的测量值比最小角度的度量高 20 度。 找出所有三个角度的测量值。
解决方案
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 所有三个角度的测量 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 放开\(a=1^{st}\)角度。 \(a+20=2^{nd}\)角度 \(90=3^{rd}\)角度(直角) |
| 画出图形并用给定的信息贴上标签 | 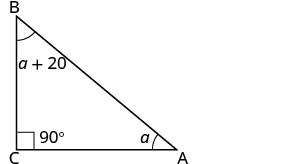 |
| 第 4 步。 翻译 | 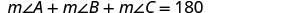 |
| 写出相应的公式。 代入配方。 |
\(a + (a + 20) + 90 = 180\) |
| 第 5 步。 求解方程。 |
\ (\ begin {align*} 2a + 110 &= 180\\ [3pt] |
| 第 6 步。 查看。 \(\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 三个角度的尺寸分别为 35°、55 ° 和 90 °。 |
直角三角形的一个角度的测量值比最小角度的测量值高 50°。 找出所有三个角度的测量值。
- 回答
-
20°,70°,90°
直角三角形的一个角度的测量值比最小角度的测量值高 30°。 找出所有三个角度的测量值。
- 回答
-
30°,60°,90°
使用毕达哥拉斯定理
我们已经了解了三角形角度的测量值是如何相互关联的。 现在,我们将学习边的长度如何相互关联。 描述直角三角形三边长度之间关系的一个重要属性称为毕达哥拉斯定理。 这个定理自古以来就在世界各地使用。 它以生活在公元前500年左右的希腊哲学家和数学家毕达哥拉斯的名字命名。
在我们陈述毕达哥拉斯定理之前,我们需要为三角形的边引入一些术语。 请记住,直角三角形的角度为 90°,角落处标有小方块。 三角形与 90°90° 角相对的一侧称为斜边,其他每边都称为腿。
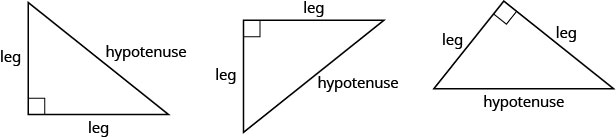
毕达哥拉斯定理讲述了直角三角形的三条边的长度是如何相互关联的。 它指出,在任何直角三角形中,两条腿长度的平方和等于斜边长度的平方。 在符号中,我们说:在任何直角三角形中\(a^{2}+b^{2}=c^{2}\),其中 a 和 b 是腿的长度,cc 是斜边的长度。
在每个练习中写下公式并在写作时大声说出来,可能有助于你记住毕达哥拉斯定理。
在任何直角三角形中,其中\(a\)和\(b\)\(c\)是腿的长度,都是斜边的长度。
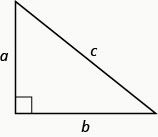
那么
\[a^{2}+b^{2}=c^{2} \label{Ptheorem}\]
要解决使用毕达哥拉斯定理(方程\ ref {Ptheorem})的练习,我们需要找到平方根。 我们使用了符号\(\sqrt{m}\)和定义:
如果\(m = n^{2}\),那么\(\sqrt{m} = n\),对于\(n\geq 0\)。
例如,我们发现这\(\sqrt{25}\)是 5,因为\(25=5^{2}\)。
由于毕达哥拉斯定理包含平方变量,因此要求解直角三角形中边的长度,我们必须使用平方根。
使用毕达哥拉斯定理找出斜边的长度,如下所示。
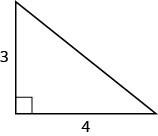
解决方案
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 三角形斜边的长度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 在图中的 c 面贴上标签。 |
假设 c = 斜边的长度。 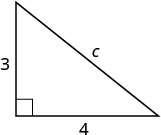 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 | \(a^{2} + b^{2} = c^{2}\) |
| 替代。 | \(3^{2}+4^{2}=c^{2}\) |
| 第 5 步。 求解方程。 | \(9+16=c^{2}\) |
| 简化。 | \(25=c^{2}\) |
| 使用平方根的定义。 | \(\sqrt{25} = c\) |
| 简化。 | \(5=c\) |
第 6 步。 查看。 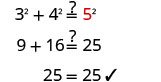 |
|
| 第 7 步。 回答问题。 | 斜边的长度为 5。 |
使用毕达哥拉斯定理在如下所示的三角形中找出斜边的长度。
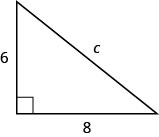
- 回答
-
c=10
使用毕达哥拉斯定理在如下所示的三角形中找出斜边的长度。
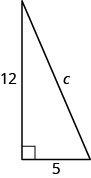
- 回答
-
c=13
使用毕达哥拉斯定理找出腿的长度,如下所示。
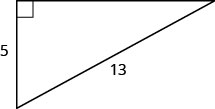
解决方案
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 三角形腿的长度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 放\(b=\)开三角形的腿。 |
| 标签面\(b\)。 | 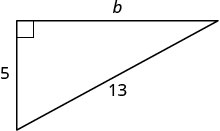 |
| 第 4 步。 翻译 | |
| 写出相应的公式。 | \(a^{2} + b^{2} = c^{2}\) |
| 替代。 | \(5^{2}+b^{2}=13^{2}\) |
| 第 5 步。 求解方程。 |
\(25+b^{2}=169\) |
| 分离变量项。 | \(b^{2}=144\) |
| 使用平方根的定义。 | \(b = \sqrt{144}\) |
| 简化。 | \(b=12\) |
第 6 步。 查看。 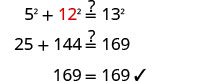 |
|
| 第 7 步。 回答问题。 | 腿的长度为 12。 |
使用毕达哥拉斯定理在如下所示的三角形中找到腿的长度。
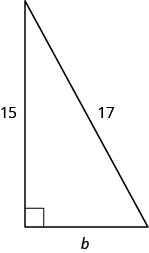
- 回答
-
8
使用毕达哥拉斯定理在如下所示的三角形中找到腿的长度。
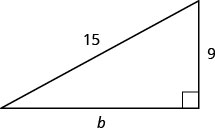
- 回答
-
12
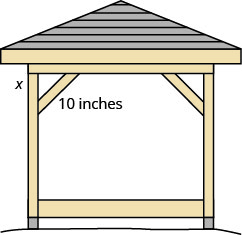
开尔文正在建造一个凉亭,他想通过在对角线上放置一块10英寸的木头来支撑每个角落,如上所示。
如果他固定木头,使支架的末端与角落的距离相同,那么直角三角形的腿的长度是多少? 近似于最接近的十分之一英寸。
解决方案
\(\begin{array} {ll} {\textbf{Step 1. }\text{Read the problem.}} &{} \\\\ {\textbf{Step 2. }\text{Identify what we are looking for.}} &{\text{the distance from the corner that the}} \\ {} &{\text{bracket should be attached}} \\ \\{\textbf{Step 3. }\text{Name. Choose a variable to represent it.}} &{\text{Let x = distance from the corner.}} \\ {\textbf{Step 4.} \text{Translate}} &{} \\ {\text{Write the appropriate formula and substitute.}} &{a^{2} + b^{2} = c^{2}} \\ {} &{x^{2} + x^{2} = 10^{2}} \\ \\ {\textbf{Step 5. Solve the equation.}} &{} \\ {} &{2x^{2} = 100} \\ {\text{Isolate the variable.}} &{x^{2} = 50} \\ {\text{Simplify. Approximate to the nearest tenth.}} &{x \approx 7.1}\\\\ {\textbf{Step 6. }\text{Check.}} &{}\\ {a^{2} + b^{2} = c^{2}} &{} \\ {(7.1)^{2} + (7.1)^{2} \approx 10^{2} \text{ Yes.}} &{} \\\\ {\textbf{Step 7. Answer the question.}} &{\text{Kelven should fasten each piece of}} \\ {} &{\text{wood approximately 7.1'' from the corner.}} \end{array}\)
约翰将一个 13 英尺长的梯子的底部放在离他家墙壁五英尺远的地方,如下所示。 梯子能到达墙上多远?

- 回答
-
12 英尺
兰迪想在帆船的15英尺桅杆顶部安装一根17英尺长的灯串,如下所示。 他应该把灯串的末端固定在离桅杆底部多远的地方?
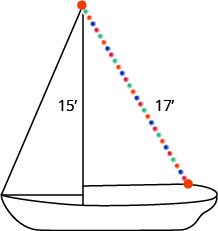
- 回答
-
8 英尺
使用矩形属性解析应用程序
你可能已经熟悉了矩形的属性。 矩形有四个边和四个直角(90°)。 矩形的两边长度相同。 我们将矩形的一边称为长度\(L\),将其相邻边称为宽度\(W\)。
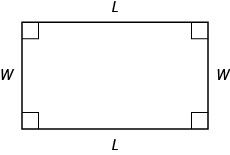
此矩形周围的距离为\(L+W+L+W\)、或\(2L+2W\)。 这是矩形\(P\)的周长。
\[P=2L+2W\]
矩形的面积呢? 想象一下 2 英尺长 x 3 英尺宽的矩形地毯。 它的面积为6平方英尺。 图中有六个方格。
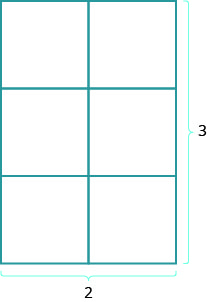
\[\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}\]
面积是长度乘以宽度。 矩形面积的公式为
\[A=LW.\]
矩形有四个边和四个直角(90°)。
两边的长度相等。
矩形的周长是长度的两倍和宽度的两倍之和。
\[P=2L+2W\]
矩形的面积是长度和宽度的乘积。
\[A=L·W\]
矩形的长度为 32 米,宽度为 20 米。 周长是多少?
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 |
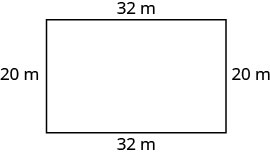 |
| 第 2 步。 确定你在找什么。 | 矩形的周长 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 让\(P=\)周长。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 |  |
| 替代。 | 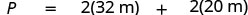 |
| 第 5 步。 求解方程。 | \(P = 64 + 40\) \(P = 104\) |
| 第 6 步。 查看。 \(\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{=}} &{104} \\ {104} &{=} &{104\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 矩形的周长为 104 米。 |
矩形的长度为 120 码,宽度为 50 码。 周长是多少?
- 回答
-
340 码
矩形的长度为 62 英尺,宽度为 48 英尺。 周长是多少?
- 回答
-
220 英尺
矩形房间的面积为 168 平方英尺。 长度为 14 英尺。 宽度是多少?
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 |
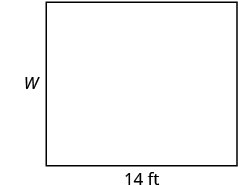 |
| 第 2 步。 确定你在找什么。 | 矩形房间的宽度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 假\(W=\)设宽度。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 | \(A=LW\) |
| 替代。 | \(168 = 14W\) |
| 第 5 步。 求解方程。 |
\(\frac{168}{14} = \frac{14W}{14}\) \(12 = W\) |
第 6 步。 查看。 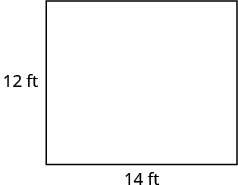 \(\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ {168} &{=} &{168\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 房间的宽度为 12 英尺。 |
矩形的面积为 598 平方英尺。 长度为 23 英尺。 宽度是多少?
- 回答
-
26 英尺
矩形的宽度为 21 米。 面积为 609 平方米。 长度是多少?
- 回答
-
29 米
找出周长 50 英寸、宽 10 英寸的矩形的长度。
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 |
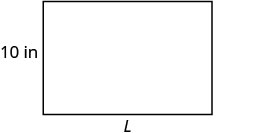 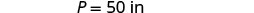 |
| 第 2 步。 确定你在找什么。 | 矩形的长度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 | 假\(L=\)设长度。 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 | \(P = 2L + 2W\) |
| 替代。 | \(50 = 2L + 2(10)\) |
| 第 5 步。 求解方程。 | 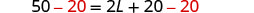 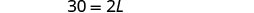 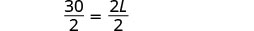  |
第 6 步。 查看。  \(\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 长度为 15 英寸。 |
找出一个矩形的长度:周长 80,宽度 25。
- 回答
-
15
找出矩形的长度:周长 30 和宽度 6。
- 回答
-
9
我们已经解决了给出长度或宽度以及周长或面积的问题;现在我们将学习如何解决根据长度定义宽度的问题。 我们将等待绘制图形,直到我们为宽度写出表达式,这样我们就可以用该表达式标记一边。
矩形的宽度比长度小两英尺。 周长为 52 英尺。 找到长度和宽度。
解决方案
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 矩形的长度和宽度 |
| 第 3 步。 姓名。 选择一个变量来表示它。 由于宽度是根据长度定义的,因此我们假设\(L=\)长度。 宽度比长度小两英尺,所以我们假设\(L-2\)宽度。 |
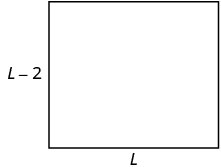 \(P=52\)英尺 |
| 第 4 步。 翻译。 | |
| 写出相应的公式。 矩形周长的公式将所有信息联系起来。 | \(P=2L+2W\) |
| 在给定的信息中替换。 | \(52=2L+2(L−2)\) |
| 第 5 步。 求解方程。 | \(52=2L+2L−4\) |
| 将相似的术语组合在一起。 | \(52=4L−4\) |
| 每边加 4 个。 | \(56 = 4L\) |
| 除以 4。 | \(\frac{56}{4} = \frac{4L}{4}\) \(14=L\) 长度为 14 英尺。 |
| 现在我们需要找到宽度。 | 宽度为\(L−2\)。  宽度为 12 英尺。 |
| 第 6 步。 查看。 因为\(14+12+14+12=52\),这行得通! 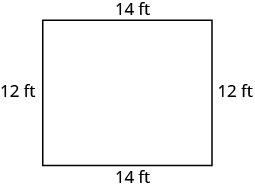 |
|
| 第 7 步。 回答问题。 | 长度为 14 英尺,宽度为 12 英尺。 |
矩形的宽度比长度小七米。 周长为 58 米。 找到长度和宽度。
- 回答
-
18 米,11 米
矩形的长度比宽度多八英尺。 周长为 60 英尺。 找到长度和宽度。
- 回答
-
19 英尺,11 英尺
矩形的长度是宽度的两倍以上的四厘米。 周长为 32 厘米。 找到长度和宽度。
解决方案
| 第 1 步。 阅读问题。 | |
| 第 2 步。 确定你在找什么。 | 长度和宽度 |
| 第 3 步。 姓名。 选择一个变量来表示宽度。 | 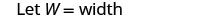 |
| 长度是四倍是宽度的两倍。 | 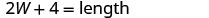 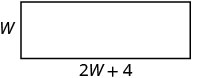 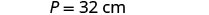 |
| 第 4 步。 翻译 | |
| 写出相应的公式。 | \(\quad P=2L+2W\) |
| 在给定的信息中替换。 | 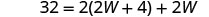 |
| 第 5 步。 求解方程。 | 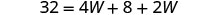 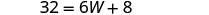 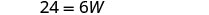 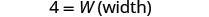 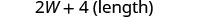  12 长度为12 厘米。 |
第 6 步。 查看。 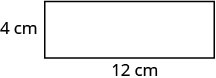 \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2\cdot 4} \\ {32} &{=} &{32\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 长度为 12 厘米,宽度为 4 厘米。 |
矩形的长度是宽度的八倍多。 周长为 64。 找到长度和宽度。
- 回答
-
24、8
矩形的宽度是六个,小于长度的两倍。 周长为 18。 找到长度和宽度。
- 回答
-
5、4
矩形游泳池的周长为 150 英尺。 长度比宽度多 15 英尺。 找到长度和宽度。
解决方案
| 第 1 步。 阅读问题。 画出图形并用给定的信息贴上标签。 |
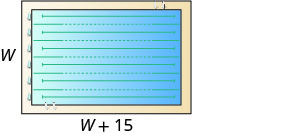 \(P=150\)英尺 |
| 第 2 步。 确定你在找什么。 | 水池的长度和宽度 |
| 第 3 步。 姓名。 选择一个变量来表示宽度。 长度比宽度多 15 英尺。 |
 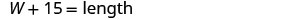 |
| 第 4 步。 翻译 | |
| 写出相应的公式。 | \(\quad P=2L+2W\) |
| 替代。 | 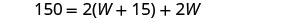 |
| 第 5 步。 求解方程。 | 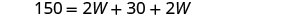 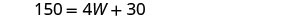      |
| 第 6 步。 查看。 \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}\) |
|
| 第 7 步。 回答问题。 | 游泳池的长度为 45 英尺,宽度为 30 英尺。 |
矩形游泳池的周长为 200 英尺。 长度比宽度多 40 英尺。 找到长度和宽度。
- 回答
-
70 英尺,30 英尺
矩形花园的长度比宽度多 30 码。 周长为 300 码。 找到长度和宽度。
- 回答
-
90 码,60 码
关键概念
- 几何应用的问题解决策略
- 阅读问题并使所有的单词和想法都被理解。 画出图形并用给定的信息标记它。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
- △ABC
角度测量的三角特性:- \(m\angle{A}+m\angle{B}+m\angle{C}=180\)
- \(P=a+b+c\)
- \(A=\frac{1}{2}bh\),b=底座,h=高度
- 毕达哥拉斯定理在任何直角三角形中,\(a^{2} + b^{2} = c^{2}\)其中\(c\)是斜边的长度,\(a\)和\(b\)是腿的长度。
- 矩形的属性
- 矩形有四个边和四个直角(90°)。
- 两边的长度相等。
- 矩形的周长是长度的两倍和宽度的两倍之和:\(P=2L+2W\)。
- 矩形的面积是长度乘以宽度:\(A=LW\).


