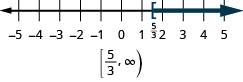第 2 章复习练习
- Page ID
- 204622
第 2 章复习练习
使用等式的减法和加法属性求解方程
验证方程的解
在以下练习中,确定每个数字是否是方程的解。
\(10 x-1=5 x ; x=\frac{1}{5}\)
\(w+2=\frac{5}{8} ; w=\frac{3}{8}\)
- 回答
-
不
\(-12 n+5=8 n ; n=-\frac{5}{4}\)
\(6 a-3=-7 a, a=\frac{3}{13}\)
- 回答
-
是的
使用等式的减法和加法属性求解方程
在以下练习中,使用等式的减法属性求解每个方程。
\(x+7=19\)
\(y+2=-6\)
- 回答
-
\(y=-8\)
\(a+\frac{1}{3}=\frac{5}{3}\)
\(n+3.6=5.1\)
- 回答
-
\(n=1.5\)
在以下练习中,使用等式的加法属性求解每个方程。
\(u-7=10\)
\(x-9=-4\)
- 回答
-
\(x=5\)
\(c-\frac{3}{11}=\frac{9}{11}\)
\(p-4.8=14\)
- 回答
-
\(p=18.8\)
在以下练习中,求解每个方程。
\(n-12=32\)
\(y+16=-9\)
- 回答
-
\(y=-25\)
\(f+\frac{2}{3}=4\)
\(d-3.9=8.2\)
- 回答
-
\(d=12.1\)
求解需要简化的方程
在以下练习中,求解每个方程。
\(y+8-15=-3\)
\(7 x+10-6 x+3=5\)
- 回答
-
\(x=-8\)
\(6(n-1)-5 n=-14\)
\(8(3 p+5)-23(p-1)=35\)
- 回答
-
\(p=-28\)
转换为方程并求解
在以下练习中,将每个英语句子翻译成一个代数方程,然后求解。
\(-6\)和的总和\(m\)为 25
四小于等\(n\)于 13
- 回答
-
\(n-4=13 ; n=17\)
翻译和解析应用程序
在以下练习中,将其转换为代数方程并求解。
罗谢尔的女儿今年11岁。 她的儿子小三岁。 她儿子多大了?
棕褐色重 146 磅。 Minh 的体重比 Tan 多 15 磅。 Minh 的重量是多少?
- 回答
-
161 磅
彼得花了9.75美元去看电影,比他去听音乐会花了46.25美元。 他为演唱会花了多少钱?
艾丽莎\(\$ 152.84\)本周的收入\(\$ 2 . .65\)超过了她上周的收入。 她上周赚了多少钱?
- 回答
-
\(\$ 131.19\)
使用等式的除法和乘法属性求解方程
使用等式的除法和乘法属性求解方程
在以下练习中,使用等式的除法和乘法属性求解每个方程并检查解。
\(8 x=72\)
\(13 a=-65\)
- 回答
-
\(a=-5\)
\(0.25 p=5.25\)
\(-y=4\)
- 回答
-
\(y=-4\)
\(\frac{n}{6}=18\)
\(\frac{y}{-10}=30\)
- 回答
-
\(y=-300\)
\(36=\frac{3}{4} x\)
\(\frac{5}{8} u=\frac{15}{16}\)
- 回答
-
\(u=\frac{3}{2}\)
\(-18 m=-72\)
\(\frac{c}{9}=36\)
- 回答
-
\(c=324\)
\(0.45 x=6.75\)
\(\frac{11}{12}=\frac{2}{3} y\)
- 回答
-
\(y=\frac{11}{8}\)
求解需要简化的方程
在以下练习中,求解每个需要简化的方程。
\(5 r-3 r+9 r=35-2\)
\(24 x+8 x-11 x=-7-14\)
- 回答
-
\(x=-1\)
\(\frac{11}{12} n-\frac{5}{6} n=9-5\)
\(-9(d-2)-15=-24\)
- 回答
-
\(d=3\)
转换为方程并求解
在以下练习中,转换为方程然后求解。
143 是\(-11\)和的产物\(y\)
and\(b\) 和 9 的商是\(-27\)
- 回答
-
\(\frac{b}{9}=-27 ; b=-243\)
q 和四分之一的总和为一。
s 和十二分之一的差值为四分之一。
- 回答
-
\(s-\frac{1}{12}=\frac{1}{4} ; s=\frac{1}{3}\)
翻译和解析应用程序
在以下练习中,将其转换为方程并求解。
雷在县集市上花了21美元购买了12张门票。 每张票的价格是多少?
珍妮特\(\$ 24\)按小时领取报酬。 她听说这是亚当\(\frac{3}{4}\)的报酬。 亚当每小时的工资是多少?
- 回答
-
32 美元
求解两边都有变量和常量的方程
求解两边都有常数的方程
在以下练习中,求解以下两边均为常数的方程。
\(8 p+7=47\)
\(10 w-5=65\)
- 回答
-
\(w=7\)
\(3 x+19=-47\)
\(32=-4-9 n\)
- 回答
-
\(n=-4\)
求解两边都有变量的方程
在以下练习中,使用两边都有变量求解以下方程。
\(7 y=6 y-13\)
\(5 a+21=2 a\)
- 回答
-
\(a=-7\)
\(k=-6 k-35\)
\(4 x-\frac{3}{8}=3 x\)
- 回答
-
\(x=\frac{3}{8}\)
求解两边都有变量和常量的方程
在以下练习中,求解两边均为变量和常量的方程。
\(12 x-9=3 x+45\)
\(5 n-20=-7 n-80\)
- 回答
-
\(n=-5\)
\(4 u+16=-19-u\)
\(\frac{5}{8} c-4=\frac{3}{8} c+4\)
- 回答
-
\(c=32\)
使用通用策略求解线性方程
使用求解线性方程的通用策略求解方程
在以下练习中,求解每个线性方程。
\(6(x+6)=24\)
\(9(2 p-5)=72\)
- 回答
-
\(p=\frac{13}{2}\)
\(-(s+4)=18\)
\(8+3(n-9)=17\)
- 回答
-
\(n=12\)
\(23-3(y-7)=8\)
\(\frac{1}{3}(6 m+21)=m-7\)
- 回答
-
\(m=-14\)
\(4(3.5 y+0.25)=365\)
\(0.25(q-8)=0.1(q+7)\)
- 回答
-
\(q=18\)
\(8(r-2)=6(r+10)\)
\(\begin{array}{l}{5+7(2-5 x)=2(9 x+1)} \\ {-(13 x-57)}\end{array}\)
- 回答
-
\(x=-1\)
\(\begin{array}{l}{(9 n+5)-(3 n-7)} \\ {=20-(4 n-2)}\end{array}\)
\(\begin{array}{l}{2[-16+5(8 k-6)]} \\ {=8(3-4 k)-32}\end{array}\)
- 回答
-
\(k=\frac{3}{4}\)
对方程进行分类
在以下练习中,将每个方程归类为条件方程、恒等方程或矛盾,然后陈述解。
\(\begin{array}{l}{17 y-3(4-2 y)=11(y-1)} \\ {+12 y-1}\end{array}\)
\(\begin{array}{l}{9 u+32=15(u-4)} \\ {-3(2 u+21)}\end{array}\)
- 回答
-
矛盾;没有解决办法
\(-8(7 m+4)=-6(8 m+9)\)
\(\begin{array}{l}{21(c-1)-19(c+1)} \\ {=2(c-20)}\end{array}\)
- 回答
-
身份;所有实数
使用分数和小数求解方程
使用分数系数求解方程
在以下练习中,使用分数系数求解每个方程。
\(\frac{2}{5} n-\frac{1}{10}=\frac{7}{10}\)
\(\frac{1}{3} x+\frac{1}{5} x=8\)
- 回答
-
\(x=15\)
\(\frac{3}{4} a-\frac{1}{3}=\frac{1}{2} a-\frac{5}{6}\)
\(\frac{1}{2}(k-3)=\frac{1}{3}(k+16)\)
- 回答
-
\(k=41\)
\(\frac{3 x-2}{5}=\frac{3 x+4}{8}\)
\(\frac{5 y-1}{3}+4=\frac{-8 y+4}{6}\)
- 回答
-
\(y=-1\)
使用十进制系数求解方程
在以下练习中,使用十进制系数求解每个方程。
\(0.8 x-0.3=0.7 x+0.2\)
\(0.36 u+2.55=0.41 u+6.8\)
- 回答
-
\(u=-85\)
\(0.6 p-1.9=0.78 p+1.7\)
\(0.6 p-1.9=0.78 p+1.7\)
- 回答
-
\(d=-20\)
求解特定变量的公式
使用距离、速率和时间公式
在以下练习中,求解。
娜塔莉以每\(\frac{1}{2}\)小时 60 英里的速度开了 7 个小时。 她走了多远的距离?
马洛里正乘公共汽车从圣路易斯去芝加哥。 距离为 300 英里,公交车以每小时 60 英里的稳定速度行驶。 乘坐公交车需要多长时间?
- 回答
-
5 个小时
亚伦的朋友开车把他从布法罗带到克利夫兰。 距离为 187 英里,行程花了 2.75 个小时。 亚伦的朋友开得多快?
林克以每小时 15 英里的稳定速度骑自行车 2 个\(\frac{1}{2}\)小时。 他走了多远的距离?
- 回答
-
37.5 英里
求解特定变量的公式
在以下练习中,求解。
使用公式。d=rt 求解 t
- 当 d=510 和 r=60 时
- 一般来说
使用公式。d=rt 求解 r
- 什么时候 d=451 和 t=5.5
- 一般来说
- 回答
-
- r=82mph
- \(r=\frac{D}{t}\)
使用公式\(A=\frac{1}{2} b h\)求解 b
- 当 A=390 和 h=26 时
- 一般来说
使用公式\(A=\frac{1}{2} b h\)求解 b
- 当 A=153 和 b=18 时
- 一般来说
- 回答
-
- \(h=17\)
- \( h=\frac{2 A}{b}\)
使用公式 I=Prt 求解主值,P 求解
- I=2,501 美元,r= 4.1%,t=5 年
- 一般来说
求解 y 的公式 4x+3y=6
- 当 x=−2 时
- 一般来说
- 回答
-
ⓐ\(y=\frac{14}{3}\) ⓑ\( y=\frac{6-4 x}{3}\)
\(180=a+b+c\)求解\(c\)
求解以下公\(V=L W H\)式\(H\)
- 回答
-
\(H=\frac{V}{L W}\)
求解线性不等式
在数字线上绘制不等式图
在以下练习中,在数字线上绘制每个不等式的图形。
- \(x\leq 4\)
- x>−2
- x<1
- x>0
- x<−3
- \(x\geq −1\)
- 回答
-
在以下练习中,在数字行上绘制每个不等式的图形,然后用间隔符号书写。
- \(x<-1\)
- \(x \geq-2.5\)
- \(x \leq \frac{5}{4}\)
- \(x>2\)
- \(x \leq-1.5\)
- \(x \geq \frac{5}{3}\)
- 回答
-
使用不等式的减法和加法属性求解不等式
在以下练习中,求解每个不等式,在数字线上绘制解图,然后用区间表示法写出解。
\(n-12 \leq 23\)
\(m+14 \leq 56\)
- 回答
-
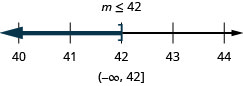
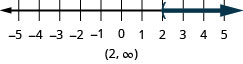
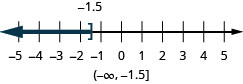
\(a+\frac{2}{3} \geq \frac{7}{12}\)
\(b-\frac{7}{8} \geq-\frac{1}{2}\)
- 回答
-
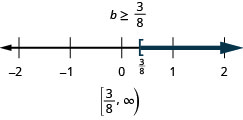
使用不等式的除法和乘法属性求解不等式
在以下练习中,求解每个不等式,在数字线上绘制解图,然后用区间表示法写出解。
\(9 x>54\)
\(-12 d \leq 108\)
- 回答
-
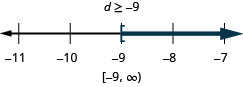
\(\frac{5}{2} j<-60\)
\(\frac{q}{-2} \geq-24\)
- 回答
-
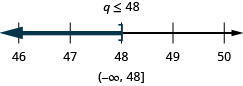
解决需要简化的不等式
在以下练习中,求解每个不等式,在数字线上绘制解图,然后用区间表示法写出解。
\(6 p>15 p-30\)
\(9 h-7(h-1) \leq 4 h-23\)
- 回答
-
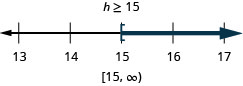
\(5 n-15(4-n)<10(n-6)+10 n\)
\(\frac{3}{8} a-\frac{1}{12} a>\frac{5}{12} a+\frac{3}{4}\)
- 回答
-
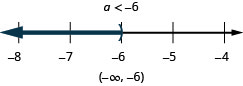
转化为不等式并求解
在以下练习中,翻译并求解。 然后用区间表示法在数字行上写下解和图形。
比 z 多五最多为 19。
小于 c 的三个至少为 360。
- 回答
-
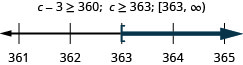
n 超过 42 的九倍。
负两倍 a 不超过 8。
- 回答
-
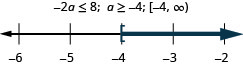
日常数学
描述一下在过去一个月里,你在数学课之外的生活中是如何使用本章中的两个主题的。
第 2 章练习测试
确定每个数字是否是方程的解\(6 x-3=x+20\)
- 5
- \(\frac{23}{5}\)
- 回答
-
- 不
- 是的
在以下练习中,求解每个方程。
\(n-\frac{2}{3}=\frac{1}{4}\)
\(\frac{9}{2} c=144\)
- 回答
-
c=32
\(4 y-8=16\)
\(-8 x-15+9 x-1=-21\)
- 回答
-
\(x=-5\)
\(-15 a=120\)
\(\frac{2}{3} x=6\)
- 回答
-
\(x=9\)
\(x-3.8=8.2\)
\(10 y=-5 y-60\)
- 回答
-
\(y=-4\)
\(8 n-2=6 n-12\)
\(9 m-2-4 m-m=42-8\)
- 回答
-
\(m=9\)
\(-5(2 x-1)=45\)
\(-(d-9)=23\)
- 回答
-
\(d=-14\)
\(\frac{1}{4}(12 m-28)=6-2(3 m-1)\)
\(2(6 x-5)-8=-22\)
- 回答
-
\(x=-\frac{1}{3}\)
\(8(3 a-5)-7(4 a-3)=20-3 a\)
\(\frac{1}{4} p-\frac{1}{3}=\frac{1}{2}\)
- 回答
-
\(p=\frac{10}{3}\)
\(0.1 d+0.25(d+8)=4.1\)
\(14 n-3(4 n+5)=-9+2(n-8)\)
- 回答
-
矛盾;没有解决办法
\(9(3 u-2)-4[6-8(u-1)]=3(u-2)\)
求解 y 的公式 x−2y=5
- 当 x=−3 时
- 一般来说
- 回答
-
- y=4
- \(y=\frac{5-x}{2}\)
在以下练习中,在数字行上绘制图表并用间隔符号书写。
\(x \geq-3.5\)
\(x<\frac{11}{4}\)
- 回答
-
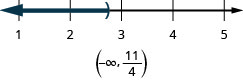
在以下练习中,求解每个不等式,在数字线上绘制解图,然后用区间表示法写出解。
\(8 k \geq 5 k-120\)
\(3 c-10(c-2)<5 c+16\)
- 回答
-
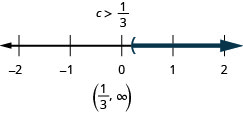
在以下练习中,转换为方程或不等式并求解。
4 少于两次 x 等于 16。
比 n 多十五至少等于 48。
- 回答
-
\(n+15 \geq 48 ; n \geq 33\)
塞缪尔本周支付了25.82美元购买汽油,比他上周支付的少了3.47美元。 他上周付了多少钱?
珍娜买了一件按原价出售\(\$ 120,\)\(\frac{2}{3}\)的外套。 这件外套的原价是多少?
- 回答
-
\(120=\frac{2}{3} p ;\)原来的价格是\(\$ 180\)
肖恩乘公共汽车从西雅图去了博伊西,距离为506英里。 如果行程花了 7\(\frac{2}{3}\) 个小时,公交车的速度是多少?