Skip to main content
Global

10.3: حل المعادلات التربيعية باستخدام الصيغة التربيعية

  1. Last updated
  2. Save as PDF
  • Page ID
    200196

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • حل المعادلات التربيعية باستخدام الصيغة التربيعية
    • استخدم التمييز للتنبؤ بعدد حلول المعادلة التربيعية
    • حدد الطريقة الأنسب لحل المعادلة التربيعية
    كن مستعدًا

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. قم بالتبسيط:\(\frac{−20−5}{10}\).
      إذا فاتتك هذه المشكلة، راجع [link].
    2. قم بالتبسيط:\(4+\sqrt{121}\).
      إذا فاتتك هذه المشكلة، راجع [link].
    3. قم بالتبسيط:\(\sqrt{128}\).
      إذا فاتتك هذه المشكلة، راجع [link].

    عندما قمنا بحل المعادلات التربيعية في القسم الأخير بإكمال المربع، اتخذنا نفس الخطوات في كل مرة. في نهاية مجموعة التمارين، ربما كنت تتساءل «أليس هناك طريقة أسهل للقيام بذلك؟» الجواب هو «نعم». في هذا القسم، سنشتق صيغة ونستخدمها لإيجاد حل المعادلة التربيعية.

    لقد رأينا بالفعل كيفية حل صيغة لمتغير معين «بشكل عام» حتى نقوم بالخطوات الجبرية مرة واحدة فقط ثم نستخدم الصيغة الجديدة للعثور على قيمة المتغير المحدد. الآن، سنتناول خطوات إكمال المربع بشكل عام لحل المعادلة التربيعية لـ x. قد يكون من المفيد إلقاء نظرة على أحد الأمثلة في نهاية القسم الأخير حيث قمنا بحل معادلة النموذج\( ax^2+bx+c=0\) أثناء قراءة الخطوات الجبرية أدناه، حتى تراها بالأرقام وكذلك «بشكل عام».

    نبدأ بالشكل القياسي للمعادلة التربيعية ونحلها لـ x بإكمال المربع. \( ax^2+bx+c=0\)
    اعزل مصطلحات المتغير على جانب واحد. \( ax^2+bx=−c\)
    اجعل المعامل الرائد 1 بالقسمة على a. \(\frac{ax^2}{a}+\frac{b}{a}x=−\frac{c}{a}\)
    قم بالتبسيط. \(x^2+\frac{b}{a}x=−\frac{c}{a}\)

    لإكمال المربع، ابحث\((\frac{1}{2}·\frac{b}{a})^2\) عنه وأضفه إلى كلا طرفي المعادلة. \((\frac{1}{2}\frac{b}{a})^2=\frac{b^2}{4a^2}\)

    		 \(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=−\frac{c}{a}+\frac{b^2}{4a^2}\)
    الجانب الأيسر هو مربع مثالي، ضعه في الاعتبار. \((x+\frac{b}{2a})^2=−\frac{c}{a}+\frac{b^2}{4a^2}\)
    أوجد المقام المشترك للجانب الأيمن واكتب الكسور المتكافئة ذات المقام المشترك. \((x+\frac{b}{2a})^2=−\frac{c·4a}{a·4a}+\frac{b^2}{4a^2}\)
    قم بالتبسيط. \((x+\frac{b}{2a})^2=\frac{b^2}{4a^2}−\frac{4ac}{4a^2}\)
    ادمج في كسر واحد. \((x+\frac{b}{2a})^2=\frac{b^2−4ac}{4a^2}\)
    استخدم خاصية الجذر التربيعي. \((x+\frac{b}{2a})=\pm\sqrt{\frac{b^2−4ac}{4a^2}}\)
    قم بالتبسيط. \((x+\frac{b}{2a})=\pm\frac{\sqrt{b^2−4ac}}{2a}\)
    أضف\(−\frac{b}{2a} \) إلى كلا طرفي المعادلة. \(x=−\frac{b}{2a}\pm\frac{\sqrt{b^2−4ac}}{2a}\)
    ادمج المصطلحات الموجودة على الجانب الأيمن. \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)

    المعادلة الأخيرة هي الصيغة التربيعية.

    تعريف: الصيغة التربيعية

    يتم إعطاء حلول المعادلة التربيعية\(a\ge 0\) للنموذج بالصيغة التالية:\(ax^2+bx+c=0\)

    \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)

    لاستخدام الصيغة التربيعية، نستبدل قيم a و b و c في التعبير الموجود على الجانب الأيمن من الصيغة. ثم نقوم بكل العمليات الحسابية لتبسيط التعبير. تعطي النتيجة الحل (الحلول) للمعادلة التربيعية.

    كيفية حل المعادلة التربيعية باستخدام الصيغة التربيعية

    مثال\(\PageIndex{1}\)

    حل\(2x^2+9x−5=0\) باستخدام الصيغة التربيعية.

    إجابة

    تُظهر الصورة خطوات حل المعادلة التربيعية: اثنان × مربع زائد تسعة × ناقص خمسة يساوي صفرًا. الخطوة الأولى هي كتابة المعادلة التربيعية في الشكل القياسي وتحديد قيم a و b و c. هذه المعادلة موجودة بالفعل في المعيار لـ. قيمة a هي اثنان، وقيمة b هي تسعة وقيمة c هي سالب خمسة.الخطوة الثانية هي كتابة الصيغة التربيعية. ثم استبدل قيم a و b و c. استبدل اثنين بـ a وتسعة بـ b وسالب خمسة عن c في الصيغة x يساوي الكمية سالب b زائد أو ناقص الجذر التربيعي لـ b التربيعي ناقص أربعة في c مقسومًا على مرتين في a. 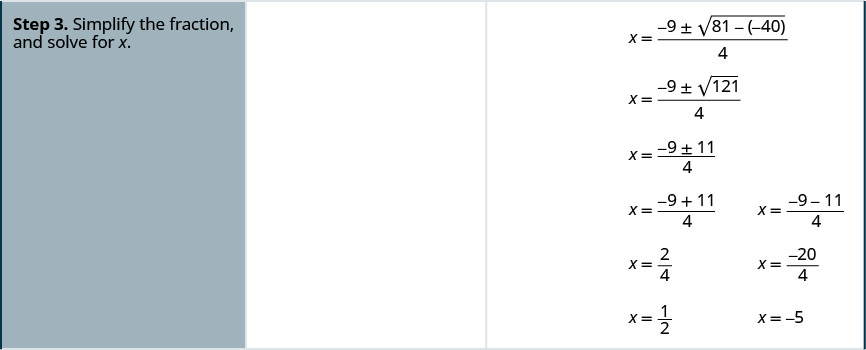تصبح الصيغة x تساوي سالب تسعة زائد أو ناقص المربع جذر سالب تسعة مربع ناقص أربعة في سالب خمسة، كل ذلك مقسومًا على اثنين في اثنين.الخطوة الثالثة هي تبسيط الصيغة. تربيع سالب تسعة وإجراء الضرب للحصول على سالب تسعة زائد أو ناقص الجذر التربيعي لـ 81 ناقص سالب 40، كل ذلك مقسومًا على أربعة. ويؤدي ذلك إلى زيادة تبسيط الجذر التربيعي لـ 121 مقسومًا على أربعة، مما يؤدي إلى تقليل سالب تسعة زائد أو ناقص 11، كل ذلك مقسومًا على أربعة. سالب تسعة زائد 11 مقسومًا على أربعة يساوي ربعين، مما يقلل إلى النصف. سالب تسعة ناقص 11 مقسومًا على أربعة يساوي سالب 20 ربعًا مما يقلل إلى سالب خمسة.الخطوة الرابعة هي التحقق من الحلول عن طريق وضع كل إجابة في المعادلة الأصلية للتحقق منها. استبدل x في اثنين x مربعًا زائد تسعة x ناقص خمسة يساوي صفرًا ونصفًا للحصول على مرتين في نصف مربع زائد تسعة في نصف واحد ناقص خمسة. قم بالتبسيط للحصول على نصف زائد تسعة أنصاف ناقص خمسة وهو صفر. استبدل x في 2 x squared زائد تسعة x ناقص خمسة يساوي صفرًا بسالب خمسة للحصول على ضربين سالب خمسة مربعًا زائد تسعة في سالب خمسة ناقص خمسة. قم بالتبسيط للحصول على 50 ناقص 45 ناقص خمسة وهو صفر.

    مثال\(\PageIndex{2}\)

    حل\(3y^2−5y+2=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(y=\frac{2}{3}\)،\(y=1\)

    مثال\(\PageIndex{3}\)

    حل\(4z^2+2z−6=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(z=−\frac{3}{2}\)،\(z=1\)

    تعريف: حل معادلة تربيعية باستخدام الصيغة التربيعية
    1. اكتب الصيغة التربيعية في الصورة القياسية. حدد قيم aa و b و c.
    2. اكتب الصيغة التربيعية. ثم استبدل قيم a و b و c.
    3. قم بالتبسيط.
    4. تحقق من الحلول.

    إذا قلت الصيغة أثناء كتابتها في كل مشكلة، فسوف يتم حفظها في أي وقت من الأوقات. وتذكر أن الصيغة التربيعية هي معادلة. تأكد من البدء بـ «\(x=\)».

    مثال\(\PageIndex{4}\)

    حل\(x^2−6x+5=0\) باستخدام الصيغة التربيعية.

    إجابة
      .
    هذه المعادلة في الشكل القياسي. .
    حدد قيم a و b و c. .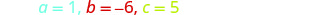
    اكتب الصيغة التربيعية. .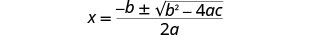
    ثم استبدل قيم أ، ب، ج. .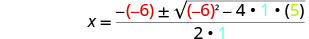
    قم بالتبسيط. .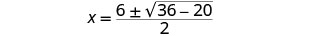
    .
    .
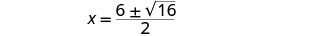
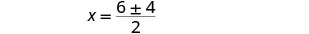
    أعد الكتابة لإظهار حلين. .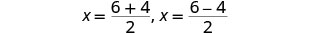
    قم بالتبسيط. .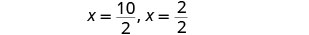
    .

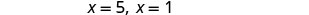
    تحقق.
    .

    		  
    مثال\(\PageIndex{5}\)

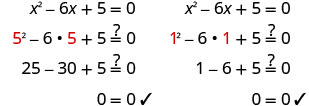
    حل\(a^2−2a−15=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(a=−3\)،\(a=5\)

    مثال\(\PageIndex{6}\)

    حل\(b^2+10b+24=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(b=−6\)،\(b=−4\)

    عندما قمنا بحل المعادلات التربيعية باستخدام خاصية الجذر التربيعي، نحصل أحيانًا على إجابات لها جذور. يمكن أن يحدث ذلك أيضًا عند استخدام الصيغة التربيعية. إذا حصلنا على حل جذري، يجب أن تحتوي الإجابة النهائية على الراديكالية في شكلها المبسط.

    مثال\(\PageIndex{7}\)

    حل\(4y^2−5y−3=0\) باستخدام الصيغة التربيعية.

    إجابة

    يمكننا استخدام الصيغة التربيعية لحل المتغير في المعادلة التربيعية، سواء كان اسمه 'x' أم لا.

      .
    هذه المعادلة في الشكل القياسي. .
    حدد قيم a و b و c. .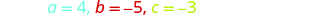
    اكتب الصيغة التربيعية. .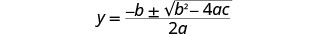
    ثم استبدل قيم أ، ب، ج. .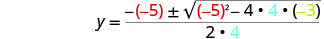
    قم بالتبسيط. .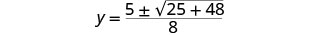
    .
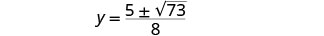
    أعد الكتابة لإظهار حلين. .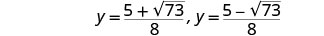
    تحقق. نترك الشيك لك.  
    مثال\(\PageIndex{8}\)

    حل\(2p^2+8p+5=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(p=\frac{−4\pm\sqrt{6}}{2}\)

    مثال\(\PageIndex{9}\)

    حل\(5q^2−11q+3=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(q=\frac{11\pm\sqrt{61}}{10}\)

    مثال\(\PageIndex{10}\)

    حل\(2x^2+10x+11=0\) باستخدام الصيغة التربيعية.

    إجابة
      .
    هذه المعادلة في الشكل القياسي. .
    حدد قيم a و b و c. .
    اكتب الصيغة التربيعية. .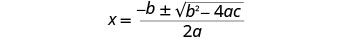
    ثم استبدل قيم أ، ب، ج. .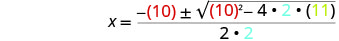
    قم بالتبسيط. .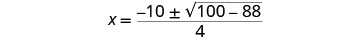
    .
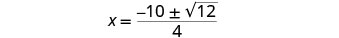
    قم بتبسيط الراديكالية. .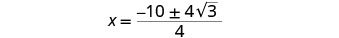
    ضع العامل المشترك في البسط في الاعتبار. .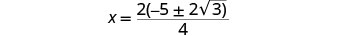
    قم بإزالة العوامل المشتركة. .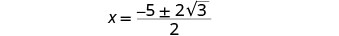
    أعد الكتابة لإظهار حلين. .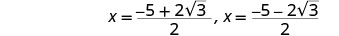
    تحقق. نترك الشيك لك.  
    مثال\(\PageIndex{11}\)

    حل\(3m^2+12m+7=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(m=\frac{−6\pm\sqrt{15}}{3}\)

    مثال\(\PageIndex{12}\)

    حل\(5n^2+4n−4=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(n=\frac{−2\pm2\sqrt{6}}{5}\)

    لا يمكننا أخذ الجذر التربيعي لعدد سالب. لذلك، عندما نستبدل أ، ب، ج في الصيغة التربيعية، إذا كانت الكمية داخل الجذر سالبة، فإن المعادلة التربيعية ليس لها حل حقيقي. سنرى هذا في المثال التالي.

    مثال\(\PageIndex{13}\)

    حل\(3p^2+2p+9=0\) باستخدام الصيغة التربيعية.

    إجابة
    هذه المعادلة في الشكل القياسي. .
    حدد قيم a و b و c. .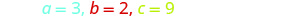
    اكتب الصيغة التربيعية. .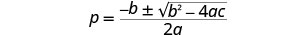
    ثم استبدل قيم أ، ب، ج. .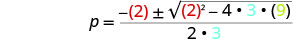
    قم بالتبسيط. .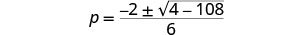
    قم بتبسيط الراديكالية. .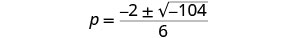
    لا يمكننا أخذ الجذر التربيعي لعدد سالب. لا يوجد حل حقيقي.
    مثال\(\PageIndex{14}\)

    حل\(4a^2−3a+8=0\) باستخدام الصيغة التربيعية.

    إجابة

    لا يوجد حل حقيقي

    مثال\(\PageIndex{15}\)

    حل\(5b^2+2b+4=0\) باستخدام الصيغة التربيعية.

    إجابة

    لا يوجد حل حقيقي

    تمت كتابة جميع المعادلات التربيعية التي قمنا بحلها حتى الآن في هذا القسم في شكل قياسي,\(ax^2+bx+c=0\). في بعض الأحيان، سنحتاج إلى إجراء بعض الجبر للحصول على المعادلة في الشكل القياسي قبل أن نتمكن من استخدام الصيغة التربيعية.

    مثال\(\PageIndex{16}\)

    حل\(x(x+6)+4=0\) باستخدام الصيغة التربيعية.

    إجابة
      .
    قم بالتوزيع للحصول على المعادلة في النموذج القياسي. .
    هذه المعادلة الآن في الشكل القياسي. .
    حدد قيم a و b و c. .
    اكتب الصيغة التربيعية. .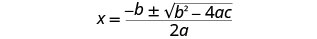
    ثم استبدل قيم أ، ب، ج. .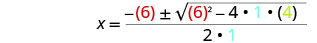
    قم بالتبسيط. .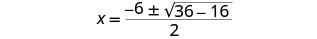
    قم بالتبسيط داخل الراديكالي. .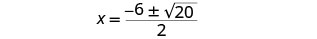
    قم بتبسيط الراديكالية. .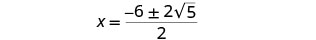
    ضع العامل المشترك في البسط في الاعتبار. .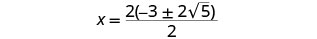
    قم بإزالة العوامل المشتركة. .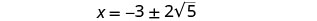
    أعد الكتابة لإظهار حلين. .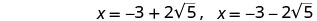
    تحقق. نترك الشيك لك.  
    مثال\(\PageIndex{17}\)

    حل\(x(x+2)−5=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(x=−1\pm\sqrt{6}\)

    مثال\(\PageIndex{18}\)

    حل\(y(3y−1)−2=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(y=−\frac{2}{3}\)،\(y=1\)

    عندما قمنا بحل المعادلات الخطية، إذا كانت المعادلة تحتوي على عدد كبير جدًا من الكسور، فإننا «نزيل الكسور» بضرب طرفي المعادلة في شاشة LCD. أعطانا هذا معادلة مكافئة - بدون كسور - لحلها. يمكننا استخدام نفس الإستراتيجية مع المعادلات التربيعية.

    مثال\(\PageIndex{19}\)

    حل\(\frac{1}{2}u^2+\frac{2}{3}u=\frac{1}{3}\) باستخدام الصيغة التربيعية.

    إجابة
      .
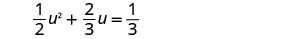
    اضرب كلا الجانبين في شاشة LCD، 6، لمسح الكسور. .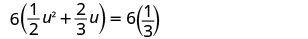
    اضرب. .
    اطرح 2 للحصول على المعادلة في الصورة القياسية. .
    حدد قيم a و b و c. .
    اكتب الصيغة التربيعية. .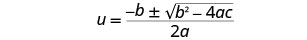
    ثم استبدل قيم أ، ب، ج. .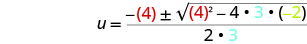
    قم بالتبسيط. .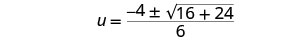
    .
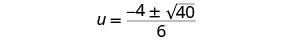
    قم بتبسيط الراديكالية. .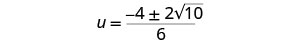
    ضع العامل المشترك في البسط في الاعتبار. .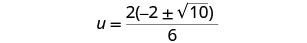
    قم بإزالة العوامل المشتركة. .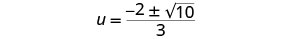
    أعد الكتابة لإظهار حلين. .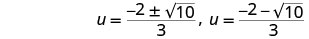
    تحقق. نترك الشيك لك.  
    مثال\(\PageIndex{20}\)

    حل\(\frac{1}{4}c^2−\frac{1}{3}c=\frac{1}{12}\) باستخدام الصيغة التربيعية.

    إجابة

    \(c=\frac{2\pm\sqrt{7}}{3}\)

    مثال\(\PageIndex{21}\)

    حل\(\frac{1}{9}d^2−\frac{1}{2}d=−\frac{1}{2}\) باستخدام الصيغة التربيعية.

    إجابة

    \(d=\frac{3}{2}\)،\(d=3\)

    فكر في المعادلة\((x−3)^2=0\). We know from the Zero Products Principle that this equation has only one solution: \(x=3\).

    سنرى في المثال التالي كيف أن استخدام الصيغة التربيعية لحل معادلة بمربع مثالي يعطي أيضًا حلًا واحدًا فقط.

    مثال\(\PageIndex{22}\)

    حل\(4x^2−20x=−25\) باستخدام الصيغة التربيعية.

    إجابة
      .
    أضف 25 للحصول على المعادلة في النموذج القياسي. .
    حدد قيم a و b و c. .
    اكتب الصيغة التربيعية. .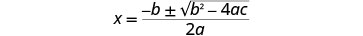
    ثم استبدل قيم أ، ب، ج. .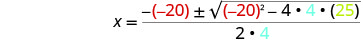
    قم بالتبسيط. .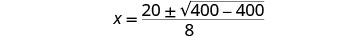
    .
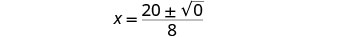
    قم بتبسيط الراديكالية. .
    قم بتبسيط الكسر. .
    تحقق. نترك الشيك لك.  

    هل أدركت أن\(4x^2−20x+25\) هذا مربع مثالي؟

    مثال\(\PageIndex{23}\)

    حل\(r^2+10r+25=0\) باستخدام الصيغة التربيعية.

    إجابة

    \(r=−5\)

    مثال\(\PageIndex{24}\)

    حل\(25t^2−40t=−16\) باستخدام الصيغة التربيعية.

    إجابة

    \(t=\frac{4}{5}\)

    استخدم التمييز للتنبؤ بعدد حلول المعادلة التربيعية

    عندما قمنا بحل المعادلات التربيعية في الأمثلة السابقة، أحيانًا نحصل على حلين، وأحيانًا حل واحد، وأحيانًا لا توجد حلول حقيقية. هل هناك طريقة للتنبؤ بعدد الحلول للمعادلة التربيعية دون حل المعادلة فعليًا؟

    نعم، الكمية الموجودة داخل جذر الصيغة التربيعية تجعل من السهل علينا تحديد عدد الحلول. هذه الكمية تسمى المميز.

    التعريف: تمييزي

    في الصيغة التربيعية\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)،\(b^2−4ac\) تُسمى الكمية بالتمييز.

    دعونا ننظر إلى تمييز المعادلات في المثال والمثال والمثال وعدد الحلول لتلك المعادلات التربيعية.

    المعادلة التربيعية (في الشكل القياسي) تمييزي\(b^2−4ac\) علامة التمييز عدد الحلول الحقيقية
    مثال \(2x^2+9x−5=0\) \ (b^2−4ac\)» data-valign= «middle» class="lt-math-15194">\(9^2−4·2(−5)=121\) + 2
    مثال \(4x^2−20x+25=0\) \ (b^2−4ac\)» data-valign= «middle» class="lt-math-15194">\((−20)^2−4·4·25=0\) 0 1
    مثال \(3p^2+2p+9=0\) \ (b^2−4ac\)» data-valign= «middle» class="lt-math-15194">\(2^2−4·3·9=−104\) − 0

    عندما يكون التمييز موجبًا\(x=\frac{−b\pm\sqrt{+}}{2a}\)، فإن المعادلة التربيعية لها حلان.

    عندما يكون التمييز صفرًا\(x=\frac{−b\pm\sqrt{0}}{2a}\)، يكون للمعادلة التربيعية حل واحد.

    عندما يكون التمييز سالبًا \(x=\frac{−b\pm\sqrt{−}}{2a}\)، لا تحتوي المعادلة التربيعية على حلول حقيقية.

    التعريف: استخدم التمييز،\(b^2−4ac\), TO DETERMINE THE NUMBER OF SolutionS OF A QUADRATIC EQUATION

    للمعادلة التربيعية للنموذج\(ax^2+bx+c=0\)،\(a \ge 0\)،

    • إذا كانت\(b^2−4ac>0\) المعادلة تحتوي على حلين.
    • إذا كان\(b^2−4ac=0\) للمعادلة حل واحد.
    • إذا كانت\(b^2−4ac<0\) المعادلة لا تحتوي على حلول حقيقية.
    مثال\(\PageIndex{25}\)

    حدد عدد الحلول لكل معادلة تربيعية:

    1. \(2v^2−3v+6=0\)
    2. \(3x^2+7x−9=0\)
    3. \(5n^2+n+4=0\)
    4. \(9y^2−6y+1=0\)
    إجابة

    1.

      \(2v^2−3v+6=0\)
    المعادلة في الشكل القياسي، حدد أ، ب، ج. \(a=2\)،\(b=−3\)،\(c=6\)
    اكتب التمييز. \(b^2−4ac\)
    استبدل قيم أ، ب، ج. \((3)^2−4·2·6\)
    قم بالتبسيط.

    \(9−48\)

    \(−39\)
    نظرًا لأن التمييز سلبي، فلا توجد حلول حقيقية للمعادلة.  

    2.

      \(3x^2+7x−9=0\)
    المعادلة في الشكل القياسي، حدد أ، ب، ج. \(a=3\)،\(b=7\)،\(c=−9\)
    اكتب التمييز. \(b^2−4ac\)
    استبدل قيم أ، ب، ج. \((7)^2−4·3·(−9)\)
    قم بالتبسيط.

    \(49+108\)

    \(157\)
    نظرًا لأن التمييز إيجابي، فهناك حلان للمعادلة.  

    3.

      \(5n^2+n+4=0\)
    المعادلة في الشكل القياسي، حدد أ، ب، ج. \(a=5\)،\(b=1\)،\(c=4\)
    اكتب التمييز. \(b^2−4ac\)
    استبدل قيم أ، ب، ج. \((1)^2−4·5·4\)
    قم بالتبسيط.

    \(1−80\)

    \(−79\)
    نظرًا لأن التمييز سلبي، فلا توجد حلول حقيقية للمعادلة.  

    4.

      \(9y^2−6y+1=0\)
    المعادلة في الشكل القياسي، حدد أ، ب، ج. \(a=9\)،\(b=−6\)،\(c=1\)
    اكتب التمييز. \(b^2−4ac\)
    استبدل قيم أ، ب، ج. \((−6)^2−4·9·1\)
    قم بالتبسيط.

    \(36−36\)

    \(0\)
    نظرًا لأن التمييز هو 0، فهناك حل واحد للمعادلة.  
    مثال\(\PageIndex{26}\)

    حدد عدد الحلول لكل معادلة تربيعية:

    1. \(8m^2−3m+6=0\)
    2. \(5z^2+6z−2=0\)
    3. \(9w^2+24w+16=0\)
    4. \(9u^2−2u+4=0\)
    إجابة
    1. لا توجد حلول حقيقية
    2. 2
    3. 1
    4. لا توجد حلول حقيقية
    مثال\(\PageIndex{27}\)

    حدد عدد الحلول لكل معادلة تربيعية:

    1. \( b^2+7b−13=0\)
    2. \(5a^2−6a+10=0\)
    3. \(4r^2−20r+25=0\)
    4. \(7t^2−11t+3=0\)
    إجابة
    1. 2
    2. لا توجد حلول حقيقية
    3. 1
    4. 2

    حدد الطريقة الأنسب لحل المعادلة التربيعية

    لقد استخدمنا أربع طرق لحل المعادلات التربيعية:

    • التخص
    • خاصية الجذر التربيعي
    • إكمال المربع
    • صيغة تربيعية

    يمكنك حل أي معادلة تربيعية باستخدام الصيغة التربيعية، ولكن هذه ليست دائمًا الطريقة الأسهل للاستخدام.

    تعريف: حدد الطريقة الأنسب لحل المعادلة التربيعية.
    1. جرب التخصيم أولاً. إذا كانت العوامل التربيعية سهلة، فإن هذه الطريقة سريعة جدًا.
    2. جرب خاصية الجذر التربيعي بعد ذلك. إذا كانت المعادلة تناسب النموذج\(ax^2=k\)\(a(x−h)^2=k\) أو يمكن حلها بسهولة باستخدام خاصية الجذر التربيعي.
    3. استخدم الصيغة التربيعية. يمكن حل أي معادلة تربيعية باستخدام الصيغة التربيعية.

    ماذا عن طريقة إكمال المربع؟ يجد معظم الناس هذه الطريقة مرهقة ويفضلون عدم استخدامها. كنا بحاجة إلى تضمينه في هذا الفصل لأننا أكملنا المربع بشكل عام لاشتقاق الصيغة التربيعية. ستستخدم أيضًا عملية إكمال المربع في مناطق الجبر الأخرى.

    مثال\(\PageIndex{28}\)

    حدد الطريقة الأنسب لاستخدامها لحل كل معادلة تربيعية:

    1. \(5z^2=17\)
    2. \(4x^2−12x+9=0\)
    3. \(8u^2+6u=11\)
    إجابة

    1. \(5z^2=17\)

    نظرًا لوجود المعادلة في\(ax^2=k\)، فإن الطريقة الأكثر ملاءمة هي استخدام خاصية الجذر التربيعي.

    2. \(4x^2−12x+9=0\)

    نحن ندرك أن الجانب الأيسر من المعادلة هو مربع ثلاثي كامل، وبالتالي فإن التحليل سيكون الطريقة الأنسب.

    3. \(8u^2+6u=11\)

    ضع المعادلة في النموذج القياسي. \(8u^2+6u−11=0\)

    في حين أن فكرتنا الأولى قد تكون تجربة التخصيم، فإن التفكير في جميع احتمالات التجربة والخطأ يقودنا إلى اختيار الصيغة التربيعية باعتبارها الطريقة الأنسب.

    مثال\(\PageIndex{29}\)

    حدد الطريقة الأنسب لاستخدامها لحل كل معادلة تربيعية:

    1. \(x^2+6x+8=0\)
    2. \((n−3)^2=16\)
    3. \(5p^2−6p=9\)
    إجابة
    1. عامل
    2. خاصية الجذر التربيعي
    3. صيغة تربيعية
    مثال\(\PageIndex{30}\)

    حدد الطريقة الأنسب لاستخدامها لحل كل معادلة تربيعية:

    1. \(8a^2+3a−9=0\)
    2. \(4b^2+4b+1=0\)
    3. \(5c2=125\)
    إجابة
    1. صيغة تربيعية
    2. العوملة
    3. خاصية الجذر التربيعي

    قم بالوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الصيغة التربيعية:

    المفاهيم الرئيسية

    • الصيغة التربيعية\(a \ge 0\) تُعطى حلول المعادلة التربيعية للنموذج بالصيغة التالية:\(ax^2+bx+c=0\)

      \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)

    • حل المعادلة التربيعية باستخدام الصيغة التربيعية
      لحل المعادلة التربيعية باستخدام الصيغة التربيعية.
      1. اكتب الصيغة التربيعية في الصورة القياسية. حدد قيم a و b و c.
      2. اكتب الصيغة التربيعية. ثم استبدل قيم أ، ب، ج.
      3. قم بالتبسيط.
      4. تحقق من الحلول.
    • استخدام التمييز\(b^2−4ac\)، لتحديد عدد حلول المعادلة التربيعية
      للمعادلة       التربيعية للنموذج\(ax^2+bx+c=0\)،\(a \ge 0\)،
      • إذا كانت\(b^2−4ac>0\) المعادلة تحتوي على حلين.
      • إذا كانت\(b^2−4ac=0\) المعادلة تحتوي على حل واحد.
      • إذا كانت\(b^2−4ac<0\) المعادلة لا تحتوي على حلول حقيقية.
    • لتحديد الطريقة الأنسب لحل المعادلة التربيعية:
      1. جرب التخصيم أولاً. إذا كانت العوامل التربيعية سهلة، فإن هذه الطريقة سريعة جدًا.
      2. جرب خاصية الجذر التربيعي بعد ذلك. إذا كانت المعادلة تناسب النموذج\(ax^2=k\)\(a(x−h)^2=k\) أو يمكن حلها بسهولة باستخدام خاصية الجذر التربيعي.
      3. استخدم الصيغة التربيعية. من الأفضل حل أي معادلة تربيعية أخرى باستخدام الصيغة التربيعية.

    مسرد المصطلحات

    تمييزي
    في الصيغة\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) التربيعية،\(b^2−4ac\) تُسمى الكمية بالتمييز.