Skip to main content
Global

10.2: حل المعادلات التربيعية بإكمال المربع

  1. Last updated
  2. Save as PDF
  • Page ID
    200195

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • أكمل مربع التعبير ذي الحدين
    • حل المعادلات التربيعية\(x^2+bx+c=0\) للنموذج بإكمال المربع
    • حل المعادلات التربيعية\(ax^2+bx+c=0\) للنموذج بإكمال المربع
    ملاحظة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا. إذا فاتتك مشكلة، فارجع إلى القسم المدرج وراجع المادة.

    1. قم بالتبسيط\((x+12)^2\).
      إذا فاتتك هذه المشكلة، راجع المثال 6.4.1.
    2. عامل\(y^2−18y+81\).
      إذا فاتتك هذه المشكلة، راجع التمرين 7.4.1.
    3. عامل\(5n^2+40n+80\).
      إذا فاتتك هذه المشكلة، راجع التمرين 7.4.13.

    حتى الآن، قمنا بحل المعادلات التربيعية عن طريق تحليل واستخدام خاصية الجذر التربيعي. في هذا القسم، سنحل المعادلات التربيعية من خلال عملية تسمى «إكمال المربع».

    أكمل مربع التعبير ذي الحدين

    في القسم الأخير، تمكنا من استخدام خاصية الجذر التربيعي لحل المعادلة\((y−7)^2=12\) لأن الجانب الأيسر كان مربعًا مثاليًا.

    \[\begin{array}{l} {(y−7)^2=12}\\ {y−7=\pm\sqrt{12}}\\ {y−7=\pm2\sqrt{3}}\\ {y=7\pm2\sqrt{3}}\\ \nonumber \end{array}\]

    لقد حللنا أيضًا معادلة يكون فيها الضلع الأيسر عبارة عن مربع ثلاثي كامل، ولكن كان علينا إعادة كتابته بالشكل من\((x−k)^2\) أجل استخدام خاصية الجذر التربيعي.

    \[\begin{array}{l} {x^2−10x+25=18}\\ {(x−5)^2=18}\\ \nonumber \end{array}\]

    ماذا يحدث إذا لم يكن المتغير جزءًا من مربع مثالي؟ هل يمكننا استخدام الجبر لإنشاء مربع مثالي؟

    دعونا ندرس نمط المربع ذي الحدين الذي استخدمناه عدة مرات. سننظر إلى مثالين.

    \[\begin{array}{ll} {(x+9)^2}&{(y−7)^2}\\ {(x+9)(x+9)}&{(y−7)(y−7)}\\ {x^2+9x+9x+81}&{y^2−7y−7y+49}\\ {x^2+18x+81}&{y^2−14y+49}\\ \nonumber \end{array}\]

    تعريف: نمط المربعات ذات الحدين

    إذا كانت أ، ب عبارة عن أرقام حقيقية،

    \((a+b)^2=a^2+2ab+b^2\)

    بديل

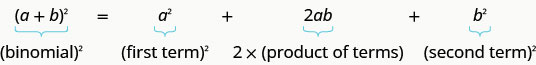
    \((a−b)^2=a^2−2ab+b^2\)

    بديل

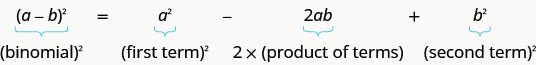
    يمكننا استخدام هذا النمط «لصنع» مربع مثالي.

    سنبدأ بالتعبير\(x^2+6x\). نظرًا لوجود علامة الجمع بين المصطلحين، سنستخدم\((a+b)^2\) النمط.

    \(a^2+2ab+b^2=(a+b)^2\)

    لاحظ أن المصطلح الأول\(x^2+6x\) هو مربع,\(x^2\).

    نحن نعلم الآن\(a=x\).

    ما العدد الذي يمكننا إضافته\(x^2+6x\) لتكوين مربع ثلاثي الحدود مثالي؟

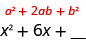
    تُظهر الصورة التعبير أ مربع زائد اثنين أ ب زائد ب مربع. يوجد أدناه التعبير x squared بالإضافة إلى ستة x بالإضافة إلى مساحة فارغة. يقع مربع x أسفل مربع a، بينما يكون x الستة أقل من 2 a b والفراغ أسفل مربع b.

    الحد الأوسط لنمط المربعات ذات الحدين، 2ab، هو ضعف حاصل ضرب مصطلحي المعادلة ذات الحدين. هذا يعني ضعف منتج x وبعض الأرقام هي 6x. لذلك، يجب أن يكون عدد ما ستة في مرتين. الرقم الذي نحتاجه هو\(\frac{1}{2}·6=3\). يجب أن يكون المصطلح الثاني في المعادلة ذات الحدين، b، 3.

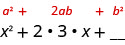
    الصورة مشابهة للصورة أعلاه. يُظهر التعبير أ مربع زائد اثنين أ ب زائد ب مربع. يوجد أدناه التعبير x squared بالإضافة إلى مرتين ثلاث مرات x بالإضافة إلى مساحة فارغة. يقع مربع x أسفل مربع a، والمضروبان في x ثلاث مرات أقل من 2 a b والفراغ أسفل مربع b.

    نحن نعلم الآن\(b=3\).

    الآن، نقوم فقط بتربيع الحد الثاني من المعادلة ذات الحدين للحصول على الحد الأخير من المربع المثالي الثلاثي، لذلك نربع ثلاثة للحصول على الحد الأخير، تسعة.

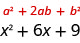
    تُظهر الصورة التعبير أ مربع زائد اثنين أ ب زائد ب مربع. يوجد أدناه التعبير x squared زائد ستة x زائد تسعة.

    يمكننا الآن مراعاة ما يلي:

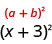
    تُظهر الصورة كمية التعبير a زائد b squared. يوجد أدناه مقدار التعبير x زائد ثلاثة مربعات.

    لذلك، وجدنا أن إضافة تسعة إلى\(x^2+6x\) «يكمل المربع»، ونكتبها كـ\((x+3)^2\).

    تعريف: أكمل المربع

    لإكمال مربع\(x^2+bx\):

    1. حدد b، معامل x.
    2. ابحث\((\frac{1}{2}b)^2\) عن الرقم المطلوب لإكمال المربع.
    3. أضف\( (\frac{1}{2}b)^2\) إلى\(x^2+bx\).
    مثال\(\PageIndex{1}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذي حدين.

    \(x^2+14x\)

    إجابة
    معامل x هو 14. .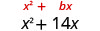

    ابحث\((\frac{1}{2}b)^2\).

    \((\frac{1}{2}⋅14)^2\)

    \((7)^2\)

    49

    		  
    أضف 49 إلى الحد ذي الحدين لإكمال المربع. \(x^2+14x+49\)
    أعد الكتابة كمربع ذو حدين. \((x+7)^2\)
    مثال\(\PageIndex{2}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(y^2+12y\)

    إجابة

    \((y+6)^2\)

    مثال\(\PageIndex{3}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(z^2+8z\)

    إجابة

    \((z+4)^2\)

    مثال\(\PageIndex{4}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين. \(m^2−26m\)

    إجابة
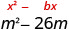
      تُظهر الصورة التعبير m squared ناقص 26 m مع x squared زائد b x مكتوبًا فوقه. معامل m هو سالب 26 لذا b هو سالب 26. ابحث عن نصف b وقم بتربيعه. نصف سالب 26 هو سالب 13 وسالب 13 مربع يساوي 169. أضف 169 إلى الحد ذي الحدين لإكمال المربع واحصل على التعبير m squared ناقص 26 m زائد 169 وهي الكمية m ناقص 13 مربعًا.

    ابحث\((\frac{1}{2}b)^2\).

    \((\frac{1}{2}⋅(−26))^2\)

    \((−13)^2\)

    169

    		  
    أضف 169 إلى الحد ذي الحدين لإكمال المربع. \(m^2−26m+169\)
    أعد الكتابة كمربع ذو حدين. \((m−13)^2\)
    مثال\(\PageIndex{5}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(a^2−20a\)

    إجابة

    \((a−10)^2\)

    مثال\(\PageIndex{6}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(b^2−4b\)

    إجابة

    \((b−2)^2\)

    مثال\(\PageIndex{7}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    \(u^2−9u\)

    إجابة
    معامل u هو −9. .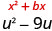

    ابحث\((\frac{1}{2}b)^2\).

    \((\frac{1}{2}⋅(−9))^2\)

    \((−\frac{9}{2})^2\)

    \(\frac{81}{4}\)

    		  
    أضف\(\frac{81}{4}\) إلى المعادلة ذات الحدين لإكمال المربع. \(u^2−9u+\frac{81}{4}\)
    أعد الكتابة كمربع ذو حدين. \((u−\frac{9}{2})^2\)
    مثال\(\PageIndex{8}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(m^2−5m\)

    إجابة

    \((m−\frac{5}{2})^2\)

    مثال\(\PageIndex{9}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(n^2+13n\)

    إجابة

    \((n+\frac{13}{2})^2\)

    مثال\(\PageIndex{10}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    \(p^2+12p\)

    إجابة
    معامل p هو\(\frac{1}{2}\) .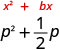

    ابحث\((\frac{1}{2}b)^2\).

    \((\frac{1}{2}⋅\frac{1}{2})^2\)

    \((\frac{1}{4})^2\)

    \(\frac{1}{16}\)

    		  
    أضف\(\frac{1}{16}\) إلى المعادلة ذات الحدين لإكمال المربع. \(p^2+\frac{1}{2}p+\frac{1}{16}\)
    أعد الكتابة كمربع ذو حدين. \((p+\frac{1}{4})^2\)
    مثال\(\PageIndex{11}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(p^2+\frac{1}{4}p\)

    إجابة

    \((p+\frac{1}{8})^2\)

    مثال\(\PageIndex{12}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. اكتب النتيجة في صورة مربع ذي حدين.

    \(q^2−\frac{2}{3}q\)

    إجابة

    \((q−\frac{1}{3})^2\)

    حل المعادلات التربيعية\(x^2 + bx + c = 0\) للنموذج بإكمال المربع

    في حل المعادلات، يجب أن نفعل دائمًا نفس الشيء لكلا طرفي المعادلة. هذا صحيح بالطبع عندما نحل المعادلة التربيعية بإكمال المربع أيضًا. عندما نضيف حدًا إلى أحد طرفي المعادلة لتكوين مربع كامل ثلاثي الحدود، يجب علينا أيضًا إضافة نفس الحد إلى الجانب الآخر من المعادلة.

    على سبيل المثال، إذا بدأنا بالمعادلة\(x^2+6x=40\) وأردنا إكمال المربع الموجود على اليسار، فسنضيف تسعة إلى كلا طرفي المعادلة.

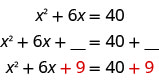
    تُظهر الصورة المعادلة x مربع زائد ستة x يساوي 40. أدناه تتم إعادة كتابة المعادلة كـ x squared بالإضافة إلى ستة x بالإضافة إلى مساحة فارغة تساوي 40 زائد مساحة فارغة. فيما يلي تتم إعادة كتابة المعادلة مرة أخرى في صورة x squared زائد ستة x زائد تسعة يساوي 40 زائد تسعة.

    ثم نركز على اليسار ونبسط الأمور على اليمين.

    \((x+3)^2=49\)

    الآن المعادلة في شكل الحل باستخدام خاصية الجذر التربيعي. يعد إكمال المربع طريقة لتحويل المعادلة إلى النموذج الذي نحتاجه حتى نتمكن من استخدام خاصية الجذر التربيعي.

    كيفية حل المعادلة التربيعية للنموذج\(x^2+bx+c=0\) بإكمال المربع.

    مثال\(\PageIndex{13}\)

    حل\(x^2+8x=48\) عن طريق إكمال المربع.

    إجابة

    توضِّح الصورة خطوات حل المعادلة x مربع زائد ثمانية x يساوي 48. الخطوة الأولى هي عزل المصطلحات المتغيرة من جانب والشروط الثابتة من جهة أخرى. تحتوي المعادلة بالفعل على جميع المتغيرات الموجودة على اليسار.الخطوة الثانية هي إيجاد نصف الكمية في مربع b، وهو الرقم الذي يجب إكمال المربع وإضافته إلى كلا طرفي المعادلة. معامل x يساوي ثمانية، لذا b يساوي ثمانية. خذ نصف العدد ثمانية، وهو أربعة، وقم بمربعه للحصول على 16. 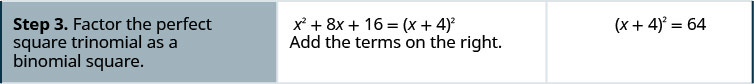أضف 16 إلى كلا طرفي المعادلة للحصول على x مربع زائد ثمانية x زائد 16 يساوي 48 زائد 16.الخطوة الثالثة هي اعتبار المربع الثلاثي المثالي كمربع ذو حدين. الجانب الأيسر هو المربع المثالي ثلاثي الحدود x مربع زائد ثمانية x زائد 16 مما يؤثر على الكمية x زائد أربعة مربعات. الإضافة على الجانب الأيمن 48 زائد 16 هي 64. المعادلة الآن هي الكمية x زائد أربعة مربعات تساوي 64.الخطوة الرابعة هي استخدام خاصية الجذر التربيعي لجعل المعادلة x زائد أربعة يساوي زائد أو ناقص الجذر التربيعي لـ 64.الخطوة الخامسة هي تبسيط الجذر ثم حل المعادلتين الناتجتين. الجذر التربيعي لـ 64 هو ثمانية. يمكن كتابة المعادلة في شكل معادلتين: x زائد أربعة يساوي ثمانية و x زائد أربعة يساوي سالب ثمانية. حل كل معادلة يعطي x يساوي أربعة أو سالب 12.الخطوة السادسة هي التحقق من الحلول. للتحقق من الحلول، ضع كل إجابة في المعادلة الأصلية. التعويض x يساوي أربعة في المعادلة الأصلية للحصول على أربعة مربعات زائد ثمانية في أربعة يساوي 48. يتم تبسيط الجانب الأيسر إلى 16 زائد 32 وهو 48. استبدال x يساوي سالب 12 في المعادلة الأصلية للحصول على سالب 12 مربعًا زائد ثمانية في سالب 12 يساوي 48. يبسط الجانب الأيسر إلى 144 ناقص 96 وهو 48.

    مثال\(\PageIndex{14}\)

    حل\(c^2+4c=5\) عن طريق إكمال المربع.

    إجابة

    \(c=−5\)،\(c=1\)

    مثال\(\PageIndex{15}\)

    حل\(d^2+10d=−9\) عن طريق إكمال المربع.

    إجابة

    \(d=−9\)،\(d=−1\)

    تعريف: حل المعادلة التربيعية للنموذج\(x^2+bx+c=0\) BY COMPLETING THE SQUARE.
    1. اعزل المصطلحات المتغيرة على أحد الجانبين والشروط الثابتة على الجانب الآخر.
    2. ابحث\((\frac{1}{2}·b)^2\) عن الرقم المطلوب لإكمال المربع. أضفه إلى كلا طرفي المعادلة.
    3. ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين.
    4. استخدم خاصية الجذر التربيعي.
    5. قم بتبسيط الجذر ثم حل المعادلتين الناتجتين.
    6. تحقق من الحلول.
    مثال\(\PageIndex{16}\)

    حل\(y^2−6y=16\) عن طريق إكمال المربع.

    إجابة
    توجد المصطلحات المتغيرة على الجانب الأيسر. .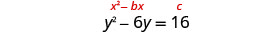

    خذ نصف −6 وقم بتربيعه. \((\frac{1}{2}(−6))^2=9\)    		 .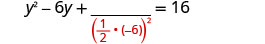
    أضف 9 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .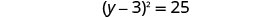
    استخدم خاصية الجذر التربيعي. .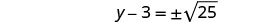
    قم بتبسيط الراديكالية. .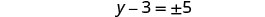
    حل من أجلك. .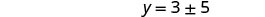
    أعد الكتابة لإظهار حلين. .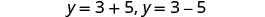
    حل المعادلات. .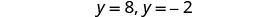

    تحقق.
    .    		  
    مثال\(\PageIndex{17}\)

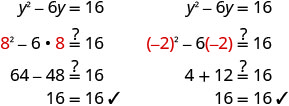
    حل\(r^2−4r=12\) عن طريق إكمال المربع.

    إجابة

    \(r=−2\)،\(r=6\)

    مثال\(\PageIndex{18}\)

    حل\(t^2−10t=11\) by completing the square.

    إجابة

    \(t=−1\)،\(t=11\)

    مثال\(\PageIndex{19}\)

    حل\(x^2+4x=−21\) عن طريق إكمال المربع.

    إجابة
    توجد المصطلحات المتغيرة على الجانب الأيسر. .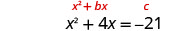

    خذ نصف 4 وقم بترتيبها. \((\frac{1}{2}(4))^2=4\)    		 .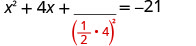
    أضف 4 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .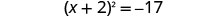
    استخدم خاصية الجذر التربيعي. .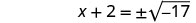
    لا يمكننا أخذ الجذر التربيعي لعدد سالب. لا يوجد حل حقيقي.
    مثال\(\PageIndex{20}\)

    حل\(y^2−10y=−35\) عن طريق إكمال المربع.

    إجابة

    لا يوجد حل حقيقي

    مثال\(\PageIndex{21}\)

    حل\(z^2+8z=−19\) عن طريق إكمال المربع.

    إجابة

    لا يوجد حل حقيقي

    في المثال السابق، لم يكن هناك حل حقيقي بسبب\((x+k)^2\) was equal to a negative number.

    مثال\(\PageIndex{22}\)

    حل\(p^2−18p=−6\) عن طريق إكمال المربع.

    إجابة
    توجد المصطلحات المتغيرة على الجانب الأيسر. .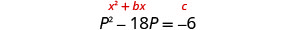
    خذ نصف −18 وقم بتربيعه. \((\frac{1}{2}(−18))^2=81\) .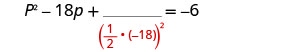
    أضف 81 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .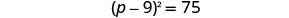
    استخدم خاصية الجذر التربيعي. .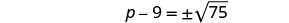
    قم بتبسيط الراديكالية. .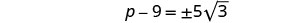
    حل لـ p. .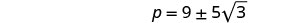
    أعد الكتابة لإظهار حلين. .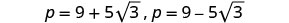

    تحقق.
    .

    		  

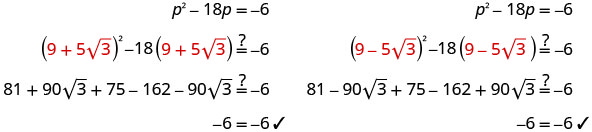
    هناك طريقة أخرى للتحقق من ذلك وهي استخدام الآلة الحاسبة. قم بتقييم\(p^2−18p\) كلا الحلين. يجب أن تكون الإجابة −6.

    مثال\(\PageIndex{23}\)

    حل\(x^2−16x=−16\) عن طريق إكمال المربع.

    إجابة

    \(x=8\pm4\sqrt{3}\)

    مثال\(\PageIndex{24}\)

    حل\(y^2+8y=11\) عن طريق إكمال المربع.

    إجابة

    \(y=−4\pm3\sqrt{3}\)

    سنبدأ المثال التالي بعزل مصطلحات المتغير على الجانب الأيسر من المعادلة.

    مثال\(\PageIndex{25}\)

    حل\(x^2+10x+4=15\) عن طريق إكمال المربع.

    إجابة
    توجد المصطلحات المتغيرة على الجانب الأيسر. .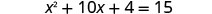
    اطرح 4 للحصول على الشروط الثابتة على الجانب الأيمن. .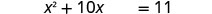

    خذ نصف 10 وقم بترتيبها. \((\frac{1}{2}(10))^2=25\)    		 .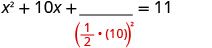
    أضف 25 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .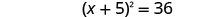
    استخدم خاصية الجذر التربيعي. .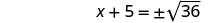
    قم بتبسيط الراديكالية. 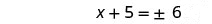مثال 10.22. JPG
    حل لـ x. .
    أعد الكتابة لإظهار معادلتين. .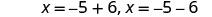
    حل المعادلات. .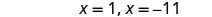

    تحقق.
    .

    		  
    مثال\(\PageIndex{26}\)

    حل\(a^2+4a+9=30\) عن طريق إكمال المربع.

    إجابة

    \(a=−7\)،\(a=3\)

    مثال\(\PageIndex{27}\)

    حل\(b^2+8b−4=16\) by completing the square.

    إجابة

    \(b=−10\)،\(b=2\)

    لحل المعادلة التالية، يجب علينا أولاً جمع كل مصطلحات المتغيرات على الجانب الأيسر من المعادلة. ثم نمضي كما فعلنا في الأمثلة السابقة.

    مثال\(\PageIndex{28}\)

    حل\(n^2=3n+11\) عن طريق إكمال المربع.

    إجابة
      .
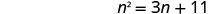
    اطرح 3 n للحصول على الشروط المتغيرة على الجانب الأيسر. .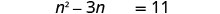
    خذ نصف −3 وقم بتربيعه. \((\frac{1}{2}(−3))^2= \frac{9}{4}\) .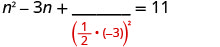
    أضف\(\frac{9}{4}\) إلى كلا الجانبين. .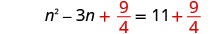
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .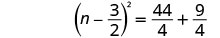
    أضف الكسور الموجودة على الجانب الأيمن. .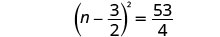
    استخدم خاصية الجذر التربيعي. .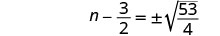
    قم بتبسيط الراديكالية. .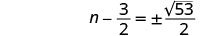
    حل لـ n. 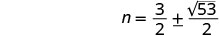مثال 10.23.JPG
    أعد الكتابة لإظهار معادلتين. .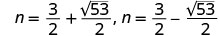
    تحقق. نترك الشيك لك!  
    مثال\(\PageIndex{29}\)

    حل\(p^2=5p+9\) عن طريق إكمال المربع.

    إجابة

    \(p=\frac{5}{2}\pm\frac{\sqrt{61}}{2}\)

    مثال\(\PageIndex{30}\)

    حل\(q^2=7q−3\) by completing the square.

    إجابة

    \(q=\frac{7}{2}\pm\frac{\sqrt{37}}{2}\)

    لاحظ أن الجانب الأيسر من المعادلة التالية هو في شكل عامل. لكن الجانب الأيمن ليس صفرًا، لذلك لا يمكننا استخدام خاصية Zero Product. بدلاً من ذلك، نضرب العوامل ثم نضع المعادلة في الصورة القياسية لحلها بإكمال المربع.

    مثال\(\PageIndex{31}\)

    حل\((x−3)(x+5)=9\) عن طريق إكمال المربع.

    إجابة
      .
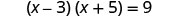
    نضرب المقادير ذات الحدين على اليسار. .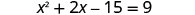
    أضف 15 للحصول على الشروط المتغيرة على الجانب الأيسر. .

    خذ نصف 2 وقم بتربيعه. \((\frac{1}{2}(2))^2=1\)    		 .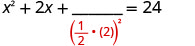
    أضف 1 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .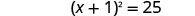
    استخدم خاصية الجذر التربيعي. .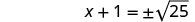
    حل لـ x. .
    أعد الكتابة لإظهار حلين. .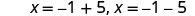
    قم بالتبسيط. .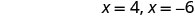
    تحقق. نترك الشيك لك!  
    مثال\(\PageIndex{32}\)

    حل\((c−2)(c+8)=7\) عن طريق إكمال المربع.

    إجابة

    \(c=−3\pm4\sqrt{2}\)

    مثال\(\PageIndex{33}\)

    حل\((d−7)(d+3)=56\) عن طريق إكمال المربع.

    إجابة

    \(d=−7\)،\(d=11\)

    حل المعادلات التربيعية\( ax^2 + bx + c = 0\) للنموذج بإكمال المربع

    تعمل عملية إكمال المربع بشكل أفضل عندما يكون المعامل الرئيسي واحدًا، لذلك يكون الجانب الأيسر من المعادلة من النموذج\(x^2+bx+c\). إذا كان\(x^2\) المصطلح يحتوي على معامل، فإننا نتخذ بعض الخطوات الأولية لجعل المعامل مساويًا لواحد.

    في بعض الأحيان يمكن حساب المعامل من جميع المصطلحات الثلاثة للثلاثية. ستكون هذه استراتيجيتنا في المثال التالي.

    مثال\(\PageIndex{34}\)

    حل\(3x^2−12x−15=0\) عن طريق إكمال المربع.

    إجابة

    لإكمال المربع، نحتاج\(x^2\) إلى معامل واحد. إذا قمنا بحساب المعامل\(x^2\) كعامل مشترك، يمكننا الاستمرار في حل المعادلة بإكمال المربع.

      .
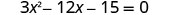
    ضع العامل المشترك الأكبر في الاعتبار. .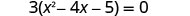
    قسّم كلا الجانبين على 3 لعزل الثلاثي. .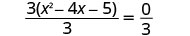
    قم بالتبسيط. .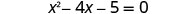
    اطرح ٥ للحصول على الشروط الثابتة على اليمين. .

    خذ نصف 4 وقم بترتيبها. \((\frac{1}{2}(4))^2=4\)    		 .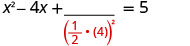
    أضف 4 إلى كلا الجانبين. .
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .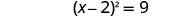
    استخدم خاصية الجذر التربيعي. .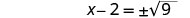
    حل لـ x. .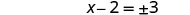
    أعد الكتابة لإظهار حلين. .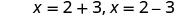
    قم بالتبسيط. .

    تحقق.
    .

    		  
    مثال\(\PageIndex{35}\)

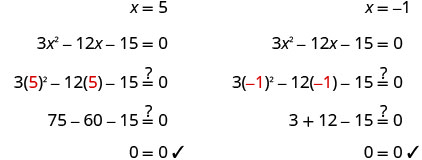
    حل\(2m^2+16m−8=0\) عن طريق إكمال المربع.

    إجابة

    \(m=−4\pm2\sqrt{5}\)

    مثال\(\PageIndex{36}\)

    حل\(4n^2−24n−56=8\) عن طريق إكمال المربع.

    إجابة

    \(n=−2, 8\)

    لإكمال المربع، يجب أن يكون المعامل الرئيسي واحدًا. عندما لا يكون المعامل الرئيسي عاملاً لجميع المصطلحات، سنقسم كلا جانبي المعادلة بالمعامل الرئيسي. سيعطينا هذا جزءًا من المعامل الثاني. لقد رأينا بالفعل كيفية إكمال المربع بالكسور في هذا القسم.

    مثال\(\PageIndex{37}\)

    حل\(2x^2−3x=20\) عن طريق إكمال المربع.

    إجابة

    مرة أخرى، ستكون خطوتنا الأولى هي جعل المعامل واحدًا.\(x^2\) بقسمة طرفي المعادلة على المعامل\(x^2\)، يمكننا عندئذٍ متابعة حل المعادلة بإكمال المربع.

      .
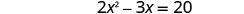
    قسّم كلا الجانبين على 2 للحصول على معامل\(x^2\) ليكون 1. .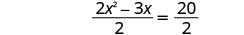
    قم بالتبسيط. .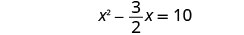

    خذ نصفها\(−\frac{3}{2}\) وقم بتجميعها. \((\frac{1}{2}(−\frac{3}{2}))^2=\frac{9}{16}\)    		 .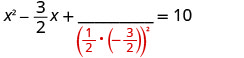
    أضف\(\frac{9}{16}\) إلى كلا الجانبين. .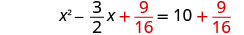
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .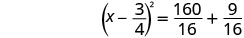
    أضف الكسور الموجودة على الجانب الأيمن. .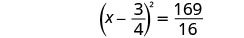
    استخدم خاصية الجذر التربيعي. .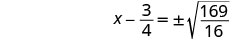
    قم بتبسيط الراديكالية. .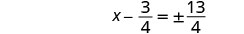
    حل لـ x. .
    أعد الكتابة لإظهار حلين. .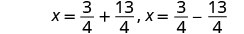
    قم بالتبسيط. .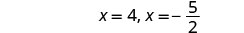
    تحقق. نترك الشيك لك.  
    مثال\(\PageIndex{38}\)

    حل\(3r^2−2r=21\) عن طريق إكمال المربع.

    إجابة

    \(r=−\frac{7}{3}\)،\(r=3\)

    مثال\(\PageIndex{39}\)

    حل\(4t^2+2t=20\) عن طريق إكمال المربع.

    إجابة

    \(t=−\frac{5}{2}\)،\(t=2\)

    مثال\(\PageIndex{40}\)

    حل\(3x^2+2x=4\) عن طريق إكمال المربع.

    إجابة

    مرة أخرى، ستكون خطوتنا الأولى هي جعل المعامل واحدًا.\(x^2\) بقسمة طرفي المعادلة على المعامل\(x^2\)، يمكننا عندئذٍ متابعة حل المعادلة بإكمال المربع.

      .
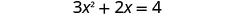
    قسّم كلا الجانبين على 3 لجعل المعامل\(x^2\) يساوي 1. .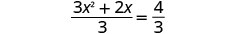
    قم بالتبسيط. .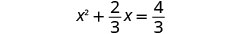

    خذ نصفها\(\frac{2}{3}\) وقم بترتيبها. \((\frac{1}{2}⋅\frac{2}{3})^2=\frac{1}{9}\)

    		 .
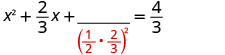
    أضف\(\frac{1}{9}\) إلى كلا الجانبين. .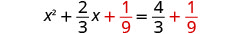
    ضع في اعتبارك المربع الثلاثي المثالي كمربع ذو حدين. .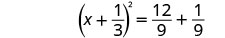
    استخدم خاصية الجذر التربيعي. .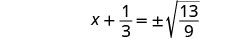
    قم بتبسيط الراديكالية. .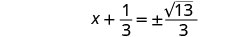
    حل لـ x. .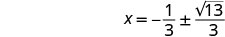
    أعد الكتابة لإظهار حلين. .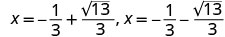
    تحقق. نترك الشيك لك. ​​​​​​​
    مثال\(\PageIndex{41}\)

    حل\(4x^2+3x=12\) عن طريق إكمال المربع.

    إجابة

    \(x=−\frac{3}{8}\pm\frac{\sqrt{201}}{8}\)

    مثال\(\PageIndex{42}\)

    حل\(5y^2+3y=10\) عن طريق إكمال المربع.

    إجابة

    \(y=−\frac{3}{10}\pm\frac{\sqrt{209}}{10}\)

    يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل المعادلات التربيعية من خلال إكمال المربع:

    المفاهيم الرئيسية

    • نمط المربعات ذات الحدين إذا كانت أ، ب، ب هي أرقام حقيقية،
      \((a+b)^2=a^2+2ab+b^2\)
      بديل
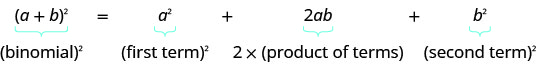
      \((a−b)^2=a^2−2ab+b^2\)
      بديل
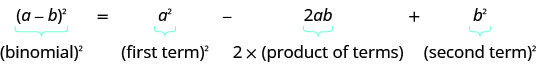
    • أكمل المربع
      لإكمال المربع الخاص بـ\(x^2+bx\):
      1. حدد bb، معامل x.
      2. ابحث\((\frac{1}{2}b)^2\) عن الرقم المطلوب لإكمال المربع.
      3. أضف\((\frac{1}{2}b)^2\) إلى\(x^2+bx\).

    مسرد المصطلحات

    إكمال المربع
    إكمال المربع هو طريقة تستخدم لحل المعادلات التربيعية.