9.7: جذور أعلى

Last updated
Save as PDF

Page ID: 200163

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

قم بتبسيط التعبيرات ذات الجذور الأعلى
استخدم خاصية المنتج لتبسيط التعبيرات ذات الجذور الأعلى
استخدم خاصية حاصل القسمة لتبسيط التعبيرات ذات الجذور الأعلى
جمع وطرح جذور أعلى

ملاحظة

قم بالتبسيط:$y^{5}y^{4}$.
إذا فاتتك هذه المشكلة، راجع المثال 6.2.7.
قم بالتبسيط:$(n^2)^6$.
إذا فاتتك هذه المشكلة، راجع المثال 6.2.19.
قم بالتبسيط:$\frac{x^8}{x^3}$.
إذا فاتتك هذه المشكلة، راجع المثال 6.5.1.

قم بتبسيط التعبيرات ذات الجذور العليا

حتى الآن، عملنا في هذا الفصل مع المربعات والجذور التربيعية. سنقوم الآن بتوسيع عملنا ليشمل القوى العليا والجذور العليا.

دعونا نراجع بعض المفردات أولاً.

\[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]

يأتي المصطلحان «مربع» و «مكعب» من معادلات مساحة المربع وحجم المكعب.

سيكون من المفيد الحصول على جدول لقوى الأعداد الصحيحة من −5to5. انظر الشكل$\PageIdnex{1}$.

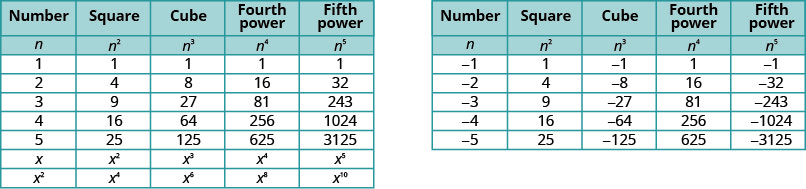
يتكون هذا الرقم من جدولين. يوضِّح الجدول الأول نتائج رفع الأرقام 1 و2 و3 و4 و5 وx والمربعة إلى القوى الثانية والثالثة والرابعة والخامسة. يوضِّح الجدول الثاني نتائج رفع الأعداد السالبة واحدة حتى سالب خمسة إلى القوى الثانية والثالثة والرابعة والخامسة. يحتوي الجدول الأول على خمسة أعمدة وتسعة صفوف. يحتوي الثاني على خمسة أعمدة وسبعة صفوف. الأعمدة في كلا الجدولين هي: «الرقم»، «المربع»، «المكعب»، «القوة الرابعة»، «القوة الخامسة»، لا شيء، «الرقم»، «المربع»، «المكعب»، «القوة الرابعة»، و «القوة الخامسة». في كلا الجدولين، يقرأ الصف التالي: n، مربع، n مكعب، n إلى القوة الرابعة، n إلى القوة الخامسة، لا شيء، n، مربع، n مكعب، n إلى القوة الرابعة، n إلى القوة الخامسة. في الجدول الأول، يظهر أن 1 مربع، و1 مكعب، و1 للقوة الرابعة، و1 للقوة الخامسة، كلها تساوي 1. في الصف التالي، مربع 2 يساوي 4، 2 مكعب يساوي 8، 2 للقوة الرابعة يساوي 16، و2 للقوة الخامسة يساوي 32. في الصف التالي، ٣ مربع يساوي ٩، ٣ مكعب يساوي ٢٧، ٣ للقوة الرابعة هي ٨١، ٣ للقوة الرابعة هي ٨١، ٣ للقوة الخامسة هي ٢٤٣. في الصف التالي، ٤ مربع يساوي ١٦، ٤ مكعبات يساوي ٦٤، ٤ للقوة الرابعة ٢٤٦، ٤ للقوة الخامسة هي ١٠٢٤. في الصف التالي، يساوي مربع ٥ يساوي ٢٥، ٥ مكعب يساوي ١٢٥، ٥ للقوة الرابعة ٦٢٥، ٥ للقوة الخامسة يساوي ٣١٢٥. في الصف التالي، يتم إدراج x squared و x المكعب و x إلى القوة الرابعة و x إلى القوة الخامسة. في الصف التالي، x مربع مربع يساوي x إلى القوة الرابعة، x المربع المكعب هو x إلى القوة الخامسة، x المربع إلى القوة الرابعة هو x إلى القوة الثامنة، و x المربّع إلى القوة الخامسة هو x إلى القوة العاشرة. في الجدول الثاني، سالب 1 مربع يساوي 1، سالب 1 المكعب هو سالب 1، سالب 1 للقوة الرابعة هو 1، وسالب 1 للقوة الخامسة هو سالب 1. في الصف التالي، سالب 2 مربع يساوي 4، سالب 2 المكعب هو سالب 8، سالب 2 للقوة الرابعة هو 16، وسالب 2 للقوة الخامسة هو سالب 32. في الصف التالي، سالب 4 مربع يساوي 16، وسالب 4 المكعب هو سالب 64، وسالب 4 للقوة الرابعة هو 256، وسالب 4 للقوة الخامسة هو سالب 1024. في الصف التالي، سالب 5 مربع يساوي 25، سالب 5 مكعب هو سالب 125، سالب 5 للقوة الرابعة هو 625، وسالب 5 للقوة الخامسة هو سالب 3125. — الشكل$\PageIndex{1}$: القوى الأولى حتى الخامسة للأعداد الصحيحة من −5 إلى 5.

لاحظ العلامات في الشكل$\PageIndex{1}$. جميع قوى الأرقام الموجبة إيجابية بالطبع. ولكن عندما يكون لدينا رقم سالب، تكون القوى الزوجية إيجابية والقوى الفردية سلبية. سنقوم بنسخ الصف الذي يحتوي على صلاحيات −2 أدناه لمساعدتك على رؤية ذلك.

$يحتوي هذا الشكل على خمسة أعمدة وصفين. يسمي الصف الأول كل عمود: n، n مربعًا، n مكعبًا، n إلى القوة الرابعة، n إلى القوة الخامسة. يقرأ الصف الثاني: سالب 2، 4، سالب 8، 16، وسالب 32.$

في وقت سابق من هذا الفصل، حددنا الجذر التربيعي لعدد.

إذا كان$n^2=m$ n هو الجذر التربيعي لـ m.

وقد استخدمنا الترميز للدلالة$\sqrt{m}$ على الجذر التربيعي الرئيسي. لذلك$\sqrt{m} \ge 0$ دائمًا.

سنقوم الآن بتوسيع التعريف ليشمل الجذور العليا.

التعريف: على جذر رقم

إذا كان$b^n=a$، ثم b هو رمز في جذر الرقم a.

يتم كتابة المبدأ الأساسي في جذر a.$\sqrt[n]{a}=b$

n يسمى مؤشر الراديكالي.

نحن لا نكتب الفهرس للجذر التربيعي. تمامًا مثلما نستخدم كلمة «مكعبة» لـ$b^3$، نستخدم مصطلح «الجذر المكعب» لـ$\sqrt[3]{a}$.

نشير إلى الشكل$\PageIndex{1}$ لمساعدتنا في العثور على جذور أعلى.

\[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]

هل يمكن أن يكون لدينا جذر زوجي لرقم سالب؟ لا. نحن نعلم أن الجذر التربيعي لعدد سالب ليس رقمًا حقيقيًا. وينطبق الشيء نفسه على أي جذر متساوٍ. حتى جذور الأرقام السالبة ليست أرقامًا حقيقية. الجذور الفردية للأرقام السالبة هي أرقام حقيقية.

تعريف: خصائص$\sqrt[n]{a}$

عندما يكون n رقمًا زوجيًا و

$a\ge 0$، إذن$\sqrt[n]{a}$ هو رقم حقيقي
$a < 0$، إذن$\sqrt[n]{a}$ ليس رقمًا حقيقيًا

عندما يكون n رقمًا فرديًا،$\sqrt[n]{a}$ يكون رقمًا حقيقيًا لجميع قيم a.

مثال$\PageIndex{1}$

قم بالتبسيط:

$\sqrt[3]{8}$
$\sqrt[4]{81}$
$\sqrt[5]{32}$.

إجابة

1.	$\sqrt[3]{8}$
منذ$(2)^3=8$.	2
2.	$\sqrt[4]{81}$
منذ$(3)^4=81$.	3
3.	$\sqrt[5]{32}$
منذ$(2)^5=32$.	2

مثال$\PageIndex{2}$

قم بالتبسيط:

$\sqrt[3]{27}$
$\sqrt[4]{256}$
$\sqrt[5]{243}$.

إجابة

مثال$\PageIndex{3}$

قم بالتبسيط:

$\sqrt[3]{1000}$
$\sqrt[4]{16}$
$\sqrt[5]{32}$.

إجابة

مثال$\PageIndex{4}$

قم بالتبسيط:

$\sqrt[3]{−64}$
$\sqrt[4]{−16}$
$\sqrt[5]{−243}$.

إجابة

1.	$\sqrt[3]{−64}$
منذ$(−4)^3=−64$.	−4
2.	$\sqrt[4]{−16}$
فكر،$(?)^4=−16$ لا يوجد رقم حقيقي يتم رفعه إلى القوة الرابعة إيجابي.	ليس رقمًا حقيقيًا.
3.	$\sqrt[5]{−243}$
منذ$(−3)^5=−243$.	−3

مثال$\PageIndex{5}$

قم بالتبسيط:

$\sqrt[3]{−125}$
$\sqrt[4]{−16}$
$\sqrt[5]{−32}$.

إجابة

−5
غير حقيقي
−2

مثال$\PageIndex{6}$

قم بالتبسيط:

$\sqrt[3]{−216}$
$\sqrt[4]{−81}$
$\sqrt[5]{−1024}$.

إجابة

−6
غير حقيقي
−4

عندما عملنا مع الجذور التربيعية التي تحتوي على متغيرات في الراديكاند، قمنا بتقييد المتغيرات إلى القيم غير السالبة. الآن سنقوم بإزالة هذا التقييد.

يمكن أن يكون الجذر الفردي للرقم موجبًا أو سلبيًا. لقد رأينا ذلك$\sqrt[3]{−64}=−4$.

لكن الجذر الزوجي للرقم غير السالب دائمًا ما يكون غير سالب، لأننا نأخذ الأساس في الجذر.

لنفترض أننا نبدأ بـ a=−5.

\[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]

كيف يمكننا التأكد من أن الجذر الرابع لـ −5 الذي تم رفعه إلى القوة الرابعة$(−5)^4$ هو 5؟ سنرى في الخاصية التالية.

التعريف: تبسيط الجذور الفردية والزوجية

لأي عدد صحيح$n \ge 2$،

\[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]

يجب أن نستخدم علامات القيمة المطلقة عندما نأخذ جذرًا متساويًا للتعبير مع متغير في الجذر.

مثال$\PageIndex{7}$

قم بالتبسيط:

$\sqrt{x^2}$
$\sqrt[3]{n^3}$
$\sqrt[4]{p^4}$
$\sqrt[5]{y^5}$.

إجابة

نحن نستخدم القيمة المطلقة للتأكد من الحصول على الجذر الإيجابي.

1.	$\sqrt{x^2}$
منذ ذلك الحين$(x)^2=x^2$ ونريد الجذر الإيجابي.	\|x\|
2.	$\sqrt[3]{n^3}$
منذ$(n)^3=n^3$. إنه جذر فردي لذا ليست هناك حاجة لعلامة القيمة المطلقة.	ن
3.	$\sqrt[4]{p^4}$
منذ ذلك الحين$(p)^4=p^4$ ونريد الجذر الإيجابي.	\|ص\|
4.	$\sqrt[5]{y^5}$
منذ$(y)^5=y^5$. إنه جذر فردي لذا ليست هناك حاجة لعلامة القيمة المطلقة.	ص

مثال$\PageIndex{8}$

قم بالتبسيط:

$\sqrt{b^2}$
$\sqrt[3]{w^3}$
$\sqrt[4]{m^4}$
$\sqrt[5]{q^5}$.

إجابة

|b|
ث
|م|
ف

مثال$\PageIndex{9}$

قم بالتبسيط:

$\sqrt{y^2}$
$\sqrt[3]{p^3}$
$\sqrt[4]{z^4}$
$\sqrt[5]{q^5}$

إجابة

مثال$\PageIndex{10}$

قم بالتبسيط:

$\sqrt[3]{y^{18}}$
$\sqrt[4]{z^8}$.

إجابة

1.	$\sqrt[3]{y^{18}}$
منذ$(y^6)^3=y^18$.	$\sqrt[3]{(y^6)^3}$
	$y^6$
2.	$\sqrt[4]{z^8}$
منذ$(z^2)^4=z^8$.	$\sqrt[4]{(z^2)^4}$
نظرًا$z^2$ لأنه إيجابي، فإننا لا نحتاج إلى علامة القيمة المطلقة.	$z^2$

مثال$\PageIndex{11}$

قم بالتبسيط:

$\sqrt[4]{u^{12}}$
$\sqrt[3]{v^{15}}$.

إجابة

$u^3$
$v^5$

مثال$\PageIndex{12}$

قم بالتبسيط:

$\sqrt[5]{c^{20}}$
$\sqrt[6]{d^{24}}$.

إجابة

$c^4$
$d^4$

مثال$\PageIndex{13}$

قم بالتبسيط:

$\sqrt[3]{64p^6}$
$\sqrt[4]{16q^{12}}$.

إجابة

1.	$\sqrt[3]{64p^6}$
أعد الكتابة$64p^6$ باسم$(4p^2)^3$.	$\sqrt[3]{(4p^2)^3}$
خذ الجذر التكعيبي.	$4p^2$
2.	$\sqrt[4]{16q^{12}}$
أعد كتابة الراديكاند كقوة رابعة.	$\sqrt[4]{(2q^3)^4}$
خذ الجذر الرابع.	$2\|q^3\|$

مثال$\PageIndex{14}$

قم بالتبسيط:

$\sqrt[3]{27x^{27}}$
$\sqrt[4]{81q^{28}}$.

إجابة

$3x^9$
$3∣q^7∣$

مثال$\PageIndex{15}$

قم بالتبسيط:

$\sqrt[3]{125p^9}$
$\sqrt[5]{243q^{25}}$

إجابة

$5p^3$
$3q^5$

استخدم خاصية المنتج لتبسيط التعبيرات ذات الجذور العليا

سنقوم بتبسيط التعبيرات ذات الجذور العليا بنفس الطريقة التي قمنا بتبسيط التعبيرات ذات الجذور التربيعية. وفي الجذر يعتبر مبسطًا إذا لم يكن يحتوي على عوامل$m^n$.

التعريف: مبسط في الجذر

$\sqrt[n]{a}$يعتبر مبسطًا إذا لم يكن هناك أي عوامل$m^n$.

سنقوم بتعميم خاصية المنتج لـ Square Roots لتضمين أي جذر صحيح$n \ge 2$.

التعريف: خاصية المنتج لـ N TH ROOTS

$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$و$\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$

متى$\sqrt[n]{a}$$\sqrt[n]{b}$ تكون أرقامًا حقيقية ولأي عدد صحيح$n \ge 2$

مثال$\PageIndex{16}$

قم بالتبسيط:

$\sqrt[3]{x^4}$
$\sqrt[4]{x^7}$.

إجابة

1.	$\sqrt[3]{x^4}$
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل مكعب مثالي.	$\sqrt[3]{x^3·x}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[3]{x^3}·\sqrt[3]{x}$
قم بالتبسيط.	$x\sqrt[3]{x}$
2.	$\sqrt[4]{x^7}$
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل طاقة رابع مثالي.	$\sqrt[4]{x^4·x^3}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[4]{x^4}·\sqrt[4]{x^3}$
قم بالتبسيط.	$\|x\|\sqrt[4]{x^3}$

مثال$\PageIndex{17}$

قم بالتبسيط:

$\sqrt[4]{y^6}$
$\sqrt[3]{z^5}$.

إجابة

$|y∣\sqrt[4]{y^2}$
$z\sqrt[3]{z^2}$

مثال$\PageIndex{18}$

قم بالتبسيط:

$\sqrt[5]{p^8}$
$\sqrt[6]{q^{13}}$.

إجابة

$p\sqrt[5]{p^3}$
$ q^2\sqrt[6]{q}$

مثال$\PageIndex{19}$

قم بالتبسيط:

$\sqrt[3]{16}$
$\sqrt[4]{243}$.

إجابة

1.	$\sqrt[3]{16}$
	$\sqrt[3]{2^4}$
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل مكعب مثالي.	$\sqrt[3]{2^3·2}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[3]{2^3}·\sqrt[3]{2}$
قم بالتبسيط.	$2\sqrt[3]{2}$
2.	$\sqrt[4]{243}$
	$\sqrt[4]{3^5}$
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل طاقة رابع مثالي.	$\sqrt[4]{3^4·3}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[4]{3^4}·\sqrt[4]{3}$
قم بالتبسيط.	$3\sqrt[4]{3}$

مثال$\PageIndex{20}$

قم بالتبسيط:

$\sqrt[3]{81}$
$\sqrt[4]{64}$.

إجابة

$3\sqrt[3]{3}$
$2\sqrt[4]{4}$

مثال$\PageIndex{21}$

قم بالتبسيط:

$\sqrt[3]{625}$
$\sqrt[4]{729}$.

إجابة

$5\sqrt[3]{5}$
$3\sqrt[4]{9}$

لا تنس استخدام علامات القيمة المطلقة عند أخذ الجذر المتساوي للتعبير الذي يحتوي على متغير في الجذر.

مثال$\PageIndex{22}$

قم بالتبسيط:

$\sqrt[3]{24x^7}$
$\sqrt[4]{80y^{14}}$.

إجابة

1.	$\sqrt[3]{24x^7}$
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	$\sqrt[3]{2^{3}x^{6}·3x}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}$
أعد كتابة الجذر الأول على النحو التالي$(2x^2)^3$	$\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}$
قم بالتبسيط.	$2x^2\sqrt[3]{3x}$
2.	$\sqrt[4]{80y^{14}}$
أعد كتابة الراديكاند كمنتج باستخدام عوامل القوة الرابعة المثالية.	$\sqrt[4]{2^{4}y^{12}·5y^2}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}$
أعد كتابة الجذر الأول على النحو التالي$(2y^3)^4$	$\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}$
قم بالتبسيط.	$2\|y^3\|\sqrt[4]{5y^2}$

مثال$\PageIndex{23}$

قم بالتبسيط:

$\sqrt[3]{54p^[10}]$
$\sqrt[4]{64q^{10}}$.

إجابة

$3p^3\sqrt[3]{2p}$
$2q^2\sqrt[4]{4q^2}$

مثال$\PageIndex{24}$

قم بالتبسيط:

$\sqrt[3]{128m^{11}}$
$\sqrt[4]{162n^7}$.

إجابة

$4m^3\sqrt[3]{2m^2}$
$3|n|\sqrt[4]{2n^3}$

مثال$\PageIndex{25}$

قم بالتبسيط:

$\sqrt[3]{−27}$
$\sqrt[4]{−16}$.

إجابة

1.	$\sqrt[3]{−27}$
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	$\sqrt[3]{(−3)^3}$
خذ الجذر التكعيبي.	−3
2.	$\sqrt[4]{−16}$
لا يوجد رقم حقيقي في المكان$n^4=−16$.	ليس رقمًا حقيقيًا.

مثال$\PageIndex{26}$

قم بالتبسيط:

$\sqrt[3]{−108}$
$\sqrt[4]{−48}$.

إجابة

$−3\sqrt[3]{4}$
غير حقيقي

مثال$\PageIndex{27}$

قم بالتبسيط:

$\sqrt[3]{−625}$
$\sqrt[4]{−324}$.

إجابة

$−5\sqrt[3]{5}$
غير حقيقي

استخدم خاصية حاصل القسمة لتبسيط التعبيرات ذات الجذور العليا

يمكننا تبسيط الجذور الأعلى باستخدام القسمة بنفس الطريقة التي قمنا بها بتبسيط الجذور التربيعية. أولاً نقوم بتبسيط أي كسور داخل الجذر.

مثال$\PageIndex{28}$

قم بالتبسيط:

$\sqrt[3]{\frac{a^8}{a^5}}$
$\sqrt[4]{\frac{a^{10}}{a^2}}$.

إجابة

1.	$\sqrt[3]{\frac{a^8}{a^5}}$
قم بتبسيط الكسر تحت الجذر أولاً.	$\sqrt[3]{a^3}$
قم بالتبسيط.	أ
2.	$\sqrt[4]{\frac{a^{10}}{a^2}}$
قم بتبسيط الكسر تحت الجذر أولاً.	$\sqrt[4]{a^8}$
أعد كتابة الجذر باستخدام عوامل القوة الرابعة المثالية.	$\sqrt[4]{(a^2)^4}$
قم بالتبسيط.	$a^2$

مثال$\PageIndex{29}$

قم بالتبسيط:

$\sqrt[4]{\frac{x^7}{x^3}}$
$\sqrt[4]{\frac{y^{17}}{y^5}}$.

إجابة

|x|
$y^3$

مثال$\PageIndex{30}$

قم بالتبسيط:

$\sqrt[3]{\frac{m^{13}}{m^7}}$
$\sqrt[5]{\frac{n^{12}}{n^2}}$.

إجابة

$m^2$
$n^2$

في السابق، استخدمنا خاصية Quotient «في الاتجاه المعاكس» لتبسيط الجذور التربيعية. الآن سنقوم بتعميم الصيغة لتشمل جذور أعلى.

تعريف: خاصية حاصل القسمة في الجذور

$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$و$\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

عندما$\sqrt[n]{a}$ and $\sqrt[n]{b}$ are real numbers, $b \ne 0$, and for any integer $n \ge 2$

التمارين الرياضية$\PageIndex{31}$

قم بالتبسيط:

$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$

إجابة

1.	$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
لا يعتبر الراديكاند مكعبًا مثاليًا، لذا استخدم خاصية Quotient للكتابة كجذر واحد.	$\sqrt[3]{\frac{−108}{2}}$
قم بتبسيط الكسر تحت الجذر.	$\sqrt[3]{−54}$
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	$\sqrt[3]{(−3)^3·2}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[3]{(−3)^3}·\sqrt[3]{2}$
قم بالتبسيط.	$−3\sqrt[3]{2}$
2.	$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$
لا يمثل أي من الراديكوند قوة رابعة مثالية، لذا استخدم خاصية Quotient للكتابة كمتطرف واحد	$\sqrt[4]{\frac{96x^7}{3x^2}}$
قم بتبسيط الكسر تحت الجذر.	$\sqrt[4]{32x^5}$
أعد كتابة الراديكاند كمنتج باستخدام عوامل القوة الرابعة المثالية.	$\sqrt[4]{2^{4}x^4·2x}$
أعد كتابة الراديكالية على أنها نتاج جذريين.	$\sqrt[4]{(2x)^4}·\sqrt[4]{2x}$
قم بالتبسيط.	$2\|x\|\sqrt[4]{2x}$

مثال$\PageIndex{32}$

قم بالتبسيط:

$\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}$

إجابة

غير حقيقي
$3|m|\sqrt[4]{2m^2}$

مثال$\PageIndex{33}$

قم بالتبسيط:

$\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}$
$\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}$.

إجابة

−4
$3|n|\sqrt[4]{2}$

إذا كان الكسر الموجود داخل الجذر لا يمكن تبسيطه، فإننا نستخدم الشكل الأول لخاصية حاصل القسمة لإعادة كتابة التعبير في صورة حاصل قسمة جذرين.

مثال$\PageIndex{34}$

قم بالتبسيط:

$\sqrt[3]{\frac{24x^7}{y^3}}$
$\sqrt[4]{\frac{48x^{10}}{y^8}}$.

إجابة

1.	$\sqrt[3]{\frac{24x^7}{y^3}}$
لا يمكن تبسيط الكسر في الراديكوند. استخدم خاصية حاصل القسمة للكتابة في صورة جذريين.	$\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}$
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	$\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}$
أعد كتابة البسط باعتباره نتاج جذريين.	$\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}$
قم بالتبسيط.	$\frac{2x^2\sqrt[3]{3x}}{y}$
2.	$\sqrt[4]{\frac{48x^{10}}{y^8}}$
لا يمكن تبسيط الكسر في الراديكوند. استخدم خاصية حاصل القسمة للكتابة في صورة جذريين.	$\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}$
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	$\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}$
أعد كتابة البسط باعتباره نتاج جذريين.	$\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}$
قم بالتبسيط.	$\frac{2x^2\sqrt[4]{3x^2}}{y^2}$

مثال$\PageIndex{35}$

قم بالتبسيط:

$\sqrt[3]{\frac{108c^{10}}{d^6}}$
$\sqrt[4]{\frac{80x^{10}}{y^5}}$.

إجابة

$\frac{3c^3\sqrt[3]{4c}}{d^2}$
$\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}$

مثال$\PageIndex{36}$

قم بالتبسيط:

$\sqrt[3]{\frac{40r^3}{s}}$
$\sqrt[4]{\frac{162m^{14}}{n^{12}}}$

إجابة

$r\sqrt[3]{\frac{40}{s}}$
$\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}$

جمع وطرح جذور أعلى

يمكننا جمع وطرح جذور أعلى كما قمنا بإضافة وطرح الجذور التربيعية. أولاً نقدم تعريفًا رسميًا للمتطرفين المتشابهين.

التعريف: مثل الراديكاليين

تسمى الجذور التي لها نفس المؤشر ونفس الجذور مثل الجذور.

مثل الراديكاليين لديهم نفس المؤشر ونفس الجذور.

$9\sqrt[4]{42x}$$−2\sqrt[4]{42x}$وهم مثل الراديكاليين.
$5\sqrt[3]{125x}$$6\sqrt[3]{125y}$وليسوا مثل الراديكاليين. الراديكاليون مختلفون.
$2\sqrt[5]{1000q}$$−4\sqrt[4]{1000q}$وليسوا مثل الراديكاليين. المؤشرات مختلفة.

نجمع ونطرح الجذور المتشابهة بنفس الطريقة التي نجمع بها ونطرح المصطلحات المتشابهة. يمكننا الإضافة$9\sqrt[4]{42x}+(−2\sqrt[4]{42x})$ والنتيجة هي$7\sqrt[4]{42x}$.

مثال$\PageIndex{37}$

قم بالتبسيط:

$\sqrt[3]{4x}+\sqrt[3]{4x}$
$4\sqrt[4]{8}−2\sqrt[4]{8}$

إجابة

1.	$\sqrt[3]{4x}+\sqrt[3]{4x}$
تتشابه الجذور، لذلك نضيف المعاملات	$2\sqrt[3]{4x}$
2.	$4\sqrt[4]{8}−2\sqrt[4]{8}$
تتشابه الجذور، لذا نطرح المعاملات.	$2\sqrt[4]{8}$

مثال$\PageIndex{38}$

قم بالتبسيط:

$\sqrt[5]{3x}+\sqrt[5]{3x}$
$3\sqrt[3]{9}−\sqrt[3]{9}$

إجابة

$2\sqrt[5]{3x}$
$2\sqrt[3]{9}$

مثال$\PageIndex{39}$

قم بالتبسيط:

$\sqrt[4]{10y}+\sqrt[4]{10y}$
$5\sqrt[6]{32}−3\sqrt[6]{32}$.

إجابة

$2\sqrt[4]{10y}$
$2\sqrt[6]{32}$

عندما لا يبدو أن التعبير يشبه الجذور، سنقوم بتبسيط كل جذر أولاً. يؤدي هذا أحيانًا إلى تعبير متشابه مع الراديكاليين.

مثال$\PageIndex{40}$

قم بالتبسيط:

$\sqrt[3]{54}−\sqrt[3]{16}$
$\sqrt[4]{48}+\sqrt[4]{243}$.

إجابة

1.	$\sqrt[3]{54}−\sqrt[3]{16}$
أعد كتابة كل جذر باستخدام عوامل المكعب المثالية.	$\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}$
أعد كتابة المكعبات المثالية.	$\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}$
قم بتبسيط الجذور حيثما أمكن ذلك.	$3\sqrt[3]{2}−2\sqrt[3]{2}$
اجمع مثل الراديكاليين.	$\sqrt[3]{2}$
2.	$\sqrt[4]{48}+\sqrt[4]{243}$
أعد الكتابة باستخدام عوامل القوة الرابعة المثالية.	$\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}$
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	$\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}$
أعد كتابة البسط باعتباره نتاج جذريين.	$2\sqrt[4]{3}+3\sqrt[4]{3}$
قم بالتبسيط.	$5\sqrt[4]{3}$

مثال$\PageIndex{41}$

قم بتبسيط:

$\sqrt[3]{192}−\sqrt[3]{81}$
$\sqrt[4]{32}+\sqrt[4]{512}$.

إجابة

$\sqrt[3]{3}$
$6\sqrt[4]{2}$

مثال$\PageIndex{42}$

قم بتبسيط:

$\sqrt[3]{108}−\sqrt[3]{250}$
$\sqrt[5]{64}+\sqrt[5]{486}$.

إجابة

$−\sqrt[3]{2}$
$5\sqrt[5]{2}$

مثال$\PageIndex{43}$

قم بتبسيط:

$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
$\sqrt[4]{162y^9}+\sqrt[4]{512y^5}$.

إجابة

1.	$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
أعد كتابة كل جذر باستخدام عوامل المكعب المثالية.	$\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}$
أعد كتابة المكعبات المثالية.	$\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}$
قم بتبسيط الجذور حيثما أمكن ذلك.	$2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})$
2.	$\sqrt[4]{162y^9}+\sqrt[4]{516y^5}$
أعد الكتابة باستخدام عوامل القوة الرابعة المثالية.	$\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}$
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	$\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}$
أعد كتابة البسط باعتباره نتاج جذريين.	$3y^2\sqrt[4]{2y}+4\|y\|\sqrt[4]{2y}$

مثال$\PageIndex{44}$

قم بتبسيط:

$\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}$
$\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}$.

إجابة

$2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}$
$3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}$

مثال$\PageIndex{45}$

قم بتبسيط:

$\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}$
$\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}$.

إجابة

$2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}$
$2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}$

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية من خلال تبسيط الجذور العليا.

تبسيط الجذور العليا
إضافة/طرح الجذور باستخدام مؤشرات أعلى

المفاهيم الرئيسية

خصائص لـ
$\sqrt[n]{a}$عندما يكون n رقمًا زوجيًا و
- $a \ge 0$، إذن$\sqrt[n]{a}$ هو رقم حقيقي
- $a < 0$، إذن$\sqrt[n]{a}$ ليس رقمًا حقيقيًا
- عندما يكون n رقمًا فرديًا،$\sqrt[n]{a}$ يكون رقمًا حقيقيًا لجميع قيم a.
- لأي عدد صحيح$n \ge 2$، عندما يكون n غريبًا$\sqrt[n]{a^n}=a$
- لأي عدد صحيح$n \ge 2$، عندما يكون n زوجيًا$\sqrt[n]{a^n}=|a|$
$\sqrt[n]{a}$يعتبر مبسطًا إذا لم يكن هناك أي عوامل$m^n$.
$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$و$\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$
$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$و$\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
للجمع بين الجذور المتشابهة، ما عليك سوى إضافة المعاملات أو طرحها مع الحفاظ على الجذور نفسها.

مسرد المصطلحات

في جذر رقم: إذا كان$b^n=a$، ثم b هو رجل في جذر a.

مبدأ على الجذر: يتم كتابة المبدأ الأساسي في جذر a$\sqrt[n]{a}$.

فهرس: $\sqrt[n]{a}$n يسمى مؤشر الراديكالي.

مثل الراديكاليين: تسمى الجذور التي لها نفس المؤشر ونفس الجذور مثل الجذور.

1.	\(\sqrt[3]{8}\)
منذ\((2)^3=8\).	2
2.	\(\sqrt[4]{81}\)
منذ\((3)^4=81\).	3
3.	\(\sqrt[5]{32}\)
منذ\((2)^5=32\).	2

1.	\(\sqrt{x^2}\)
منذ ذلك الحين\((x)^2=x^2\) ونريد الجذر الإيجابي.	\|x\|
2.	\(\sqrt[3]{n^3}\)
منذ\((n)^3=n^3\). إنه جذر فردي لذا ليست هناك حاجة لعلامة القيمة المطلقة.	ن
3.	\(\sqrt[4]{p^4}\)
منذ ذلك الحين\((p)^4=p^4\) ونريد الجذر الإيجابي.	\|ص\|
4.	\(\sqrt[5]{y^5}\)
منذ\((y)^5=y^5\). إنه جذر فردي لذا ليست هناك حاجة لعلامة القيمة المطلقة.	ص

1.	\(\sqrt[3]{y^{18}}\)
منذ\((y^6)^3=y^18\).	\(\sqrt[3]{(y^6)^3}\)
	\(y^6\)
2.	\(\sqrt[4]{z^8}\)
منذ\((z^2)^4=z^8\).	\(\sqrt[4]{(z^2)^4}\)
نظرًا\(z^2\) لأنه إيجابي، فإننا لا نحتاج إلى علامة القيمة المطلقة.	\(z^2\)

1.	\(\sqrt[3]{64p^6}\)
أعد الكتابة\(64p^6\) باسم\((4p^2)^3\).	\(\sqrt[3]{(4p^2)^3}\)
خذ الجذر التكعيبي.	\(4p^2\)
2.	\(\sqrt[4]{16q^{12}}\)
أعد كتابة الراديكاند كقوة رابعة.	\(\sqrt[4]{(2q^3)^4}\)
خذ الجذر الرابع.	\(2\|q^3\|\)

1.	\(\sqrt[3]{16}\)
	\(\sqrt[3]{2^4}\)
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل مكعب مثالي.	\(\sqrt[3]{2^3·2}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[3]{2^3}·\sqrt[3]{2}\)
قم بالتبسيط.	\(2\sqrt[3]{2}\)
2.	\(\sqrt[4]{243}\)
	\(\sqrt[4]{3^5}\)
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل طاقة رابع مثالي.	\(\sqrt[4]{3^4·3}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[4]{3^4}·\sqrt[4]{3}\)
قم بالتبسيط.	\(3\sqrt[4]{3}\)

1.	\(\sqrt[3]{−64}\)
منذ\((−4)^3=−64\).	−4
2.	\(\sqrt[4]{−16}\)
فكر،\((?)^4=−16\) لا يوجد رقم حقيقي يتم رفعه إلى القوة الرابعة إيجابي.	ليس رقمًا حقيقيًا.
3.	\(\sqrt[5]{−243}\)
منذ\((−3)^5=−243\).	−3

1.	\(\sqrt[3]{x^4}\)
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل مكعب مثالي.	\(\sqrt[3]{x^3·x}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[3]{x^3}·\sqrt[3]{x}\)
قم بالتبسيط.	\(x\sqrt[3]{x}\)
2.	\(\sqrt[4]{x^7}\)
أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل طاقة رابع مثالي.	\(\sqrt[4]{x^4·x^3}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[4]{x^4}·\sqrt[4]{x^3}\)
قم بالتبسيط.	\(\|x\|\sqrt[4]{x^3}\)

1.	\(\sqrt[3]{24x^7}\)
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	\(\sqrt[3]{2^{3}x^{6}·3x}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\)
أعد كتابة الجذر الأول على النحو التالي\((2x^2)^3\)	\(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\)
قم بالتبسيط.	\(2x^2\sqrt[3]{3x}\)
2.	\(\sqrt[4]{80y^{14}}\)
أعد كتابة الراديكاند كمنتج باستخدام عوامل القوة الرابعة المثالية.	\(\sqrt[4]{2^{4}y^{12}·5y^2}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\)
أعد كتابة الجذر الأول على النحو التالي\((2y^3)^4\)	\(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\)
قم بالتبسيط.	\(2\|y^3\|\sqrt[4]{5y^2}\)

1.	\(\sqrt[3]{−27}\)
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	\(\sqrt[3]{(−3)^3}\)
خذ الجذر التكعيبي.	−3
2.	\(\sqrt[4]{−16}\)
لا يوجد رقم حقيقي في المكان\(n^4=−16\).	ليس رقمًا حقيقيًا.

1.	\(\sqrt[3]{\frac{a^8}{a^5}}\)
قم بتبسيط الكسر تحت الجذر أولاً.	\(\sqrt[3]{a^3}\)
قم بالتبسيط.	أ
2.	\(\sqrt[4]{\frac{a^{10}}{a^2}}\)
قم بتبسيط الكسر تحت الجذر أولاً.	\(\sqrt[4]{a^8}\)
أعد كتابة الجذر باستخدام عوامل القوة الرابعة المثالية.	\(\sqrt[4]{(a^2)^4}\)
قم بالتبسيط.	\(a^2\)

1.	\(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
لا يعتبر الراديكاند مكعبًا مثاليًا، لذا استخدم خاصية Quotient للكتابة كجذر واحد.	\(\sqrt[3]{\frac{−108}{2}}\)
قم بتبسيط الكسر تحت الجذر.	\(\sqrt[3]{−54}\)
أعد كتابة الراديكاند كمنتج باستخدام عوامل المكعب المثالية.	\(\sqrt[3]{(−3)^3·2}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\)
قم بالتبسيط.	\(−3\sqrt[3]{2}\)
2.	\(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
لا يمثل أي من الراديكوند قوة رابعة مثالية، لذا استخدم خاصية Quotient للكتابة كمتطرف واحد	\(\sqrt[4]{\frac{96x^7}{3x^2}}\)
قم بتبسيط الكسر تحت الجذر.	\(\sqrt[4]{32x^5}\)
أعد كتابة الراديكاند كمنتج باستخدام عوامل القوة الرابعة المثالية.	\(\sqrt[4]{2^{4}x^4·2x}\)
أعد كتابة الراديكالية على أنها نتاج جذريين.	\(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\)
قم بالتبسيط.	\(2\|x\|\sqrt[4]{2x}\)

1.	\(\sqrt[3]{\frac{24x^7}{y^3}}\)
لا يمكن تبسيط الكسر في الراديكوند. استخدم خاصية حاصل القسمة للكتابة في صورة جذريين.	\(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\)
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	\(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\)
أعد كتابة البسط باعتباره نتاج جذريين.	\(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\)
قم بالتبسيط.	\(\frac{2x^2\sqrt[3]{3x}}{y}\)
2.	\(\sqrt[4]{\frac{48x^{10}}{y^8}}\)
لا يمكن تبسيط الكسر في الراديكوند. استخدم خاصية حاصل القسمة للكتابة في صورة جذريين.	\(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\)
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	\(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\)
أعد كتابة البسط باعتباره نتاج جذريين.	\(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\)
قم بالتبسيط.	\(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)

1.	\(\sqrt[3]{4x}+\sqrt[3]{4x}\)
تتشابه الجذور، لذلك نضيف المعاملات	\(2\sqrt[3]{4x}\)
2.	\(4\sqrt[4]{8}−2\sqrt[4]{8}\)
تتشابه الجذور، لذا نطرح المعاملات.	\(2\sqrt[4]{8}\)

1.	\(\sqrt[3]{54}−\sqrt[3]{16}\)
أعد كتابة كل جذر باستخدام عوامل المكعب المثالية.	\(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\)
أعد كتابة المكعبات المثالية.	\(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\)
قم بتبسيط الجذور حيثما أمكن ذلك.	\(3\sqrt[3]{2}−2\sqrt[3]{2}\)
اجمع مثل الراديكاليين.	\(\sqrt[3]{2}\)
2.	\(\sqrt[4]{48}+\sqrt[4]{243}\)
أعد الكتابة باستخدام عوامل القوة الرابعة المثالية.	\(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\)
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	\(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\)
أعد كتابة البسط باعتباره نتاج جذريين.	\(2\sqrt[4]{3}+3\sqrt[4]{3}\)
قم بالتبسيط.	\(5\sqrt[4]{3}\)

1.	\(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
أعد كتابة كل جذر باستخدام عوامل المكعب المثالية.	\(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\)
أعد كتابة المكعبات المثالية.	\(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\)
قم بتبسيط الجذور حيثما أمكن ذلك.	\(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\)
2.	\(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\)
أعد الكتابة باستخدام عوامل القوة الرابعة المثالية.	\(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\)
أعد كتابة كل جذر كمنتج باستخدام عوامل المكعب المثالية.	\(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\)
أعد كتابة البسط باعتباره نتاج جذريين.	\(3y^2\sqrt[4]{2y}+4\|y\|\sqrt[4]{2y}\)

أهداف التعلم

ملاحظة

قم بتبسيط التعبيرات ذات الجذور العليا

التعريف: على جذر رقم

تعريف: خصائص\(\sqrt[n]{a}\)

مثال\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

مثال\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

مثال\(\PageIndex{6}\)

التعريف: تبسيط الجذور الفردية والزوجية

مثال\(\PageIndex{7}\)

مثال\(\PageIndex{8}\)

مثال\(\PageIndex{9}\)

مثال\(\PageIndex{10}\)

مثال\(\PageIndex{11}\)

مثال\(\PageIndex{12}\)

مثال\(\PageIndex{13}\)

مثال\(\PageIndex{14}\)

مثال\(\PageIndex{15}\)

استخدم خاصية المنتج لتبسيط التعبيرات ذات الجذور العليا

التعريف: مبسط في الجذر

التعريف: خاصية المنتج لـ N TH ROOTS

مثال\(\PageIndex{16}\)

مثال\(\PageIndex{17}\)

مثال\(\PageIndex{18}\)

مثال\(\PageIndex{19}\)

مثال\(\PageIndex{20}\)

مثال\(\PageIndex{21}\)

مثال\(\PageIndex{22}\)

مثال\(\PageIndex{23}\)

مثال\(\PageIndex{24}\)

مثال\(\PageIndex{25}\)

مثال\(\PageIndex{26}\)

مثال\(\PageIndex{27}\)

استخدم خاصية حاصل القسمة لتبسيط التعبيرات ذات الجذور العليا

مثال\(\PageIndex{28}\)

مثال\(\PageIndex{29}\)

مثال\(\PageIndex{30}\)

تعريف: خاصية حاصل القسمة في الجذور

التمارين الرياضية\(\PageIndex{31}\)

مثال\(\PageIndex{32}\)

مثال\(\PageIndex{33}\)

مثال\(\PageIndex{34}\)

مثال\(\PageIndex{35}\)

مثال\(\PageIndex{36}\)

جمع وطرح جذور أعلى

التعريف: مثل الراديكاليين

مثال\(\PageIndex{37}\)

مثال\(\PageIndex{38}\)

مثال\(\PageIndex{39}\)

مثال\(\PageIndex{40}\)

مثال\(\PageIndex{41}\)

مثال\(\PageIndex{42}\)

مثال\(\PageIndex{43}\)

مثال\(\PageIndex{44}\)

مثال\(\PageIndex{45}\)

المفاهيم الرئيسية

مسرد المصطلحات