6.7: الأسس الصحيحة والترميز العلمي
- Page ID
- 200430
في نهاية هذا القسم، ستكون قادرًا على:
- استخدم تعريف الأس السالب
- قم بتبسيط التعبيرات باستخدام أسس عددية
- التحويل من الترميز العشري إلى الترميز العلمي
- تحويل الترميز العلمي إلى الصورة العشرية
- الضرب والقسمة باستخدام الترميز العلمي
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- ما القيمة المكانية للعدد ٦ في الرقم ٦٤٨٩١؟
إذا فاتتك هذه المشكلة، راجع التمرين 1.2.1. - قم بتسمية الرقم العشري: 0.0012.
إذا فاتتك هذه المشكلة، راجع التمرين 1.8.1. - الطرح: 5− (−3).
إذا فاتتك هذه المشكلة، راجع التمرين 1.4.33.
استخدم تعريف الأس السالب
لقد رأينا أن خاصية خارج القسمة للأسس، التي تم تقديمها سابقًا في هذا الفصل، لها شكلان يعتمدان على ما إذا كان الأس أكبر في البسط أو المقام.
إذا كان a رقمًا حقيقيًا\(a\neq0\)، و m و n عبارة عن أرقام صحيحة، إذن
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]
و
\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
ماذا لو طرحنا الأسس فقط بغض النظر عن الأكبر منها؟
دعونا نفكر\(\dfrac{x^{2}}{x^{5}}\).
نطرح الأس في المقام من الأس في البسط.
\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]
يمكننا أيضًا التبسيط\(\dfrac{x^{2}}{x^{5}}\) من خلال تقسيم العوامل المشتركة:
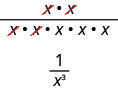
هذا يعني ذلك\(x^{-3}=\dfrac{1}{x^{3}}\) ويقودنا إلى تعريف الأس السالب.
إذا كان n عددًا صحيحًا\(a\neq 0\)، ثم\(a^{-n}=\dfrac{1}{a^{n}}\)
يخبرنا الأس السالب أنه يمكننا إعادة كتابة المقدار بأخذ مقلوب القاعدة ثم تغيير علامة الأس.
لا يعتبر أي تعبير يحتوي على أسس سالبة في أبسط صورة. سنستخدم تعريف الأس السالب والخصائص الأخرى للأسس لكتابة التعبير بالأسس الموجبة فقط.
على سبيل المثال، إذا انتهى الأمر بالتعبير بعد تبسيط التعبير\(x^{-3}\)، فسوف نتخذ خطوة أخرى ونكتب\(\dfrac{1}{x^{3}}\). تعتبر الإجابة في أبسط صورة عندما تحتوي على أسس موجبة فقط.
قم بالتبسيط:
- \(4^{-2}\)
- \(10^{-3}\)
- إجابة
-
- \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
- \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)
قم بالتبسيط:
- \(2^{-3}\)
- \(10^{-7}\)
- إجابة
-
- \(\dfrac{1}{8}\)
- \(\dfrac{1}{10^{7}}\)
قم بالتبسيط:
- \(3^{-2}\)
- \(10^{-4}\)
- إجابة
-
- \(\dfrac{1}{9}\)
- \(\dfrac{1}{10,000}\)
في التمرين،\(\PageIndex{1}\) رفعنا عددًا صحيحًا إلى أس سالب. ماذا يحدث عندما نرفع الكسر إلى أس سالب؟ سنبدأ بالنظر إلى ما يحدث للكسر الذي يكون بسطه واحدًا ومقامه عدد صحيح مرفوع إلى أس سالب.
\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)
يؤدي هذا إلى خاصية الأسس السالبة.
إذا كان n عددًا صحيحًا\(a\neq 0\)، ثم\(\dfrac{1}{a^{-n}}=a^{n}\).
قم بالتبسيط:
- \(\dfrac{1}{y^{-4}}\)
- \(\dfrac{1}{3^{-2}}\)
- إجابة
-
- \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
- \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)
قم بالتبسيط:
- \(\dfrac{1}{p^{-8}}\)
- \(\dfrac{1}{4^{-3}}\)
- إجابة
-
- \(p^{8}\)
- 64
قم بالتبسيط:
- \(\dfrac{1}{q^{-7}}\)
- \(\dfrac{1}{2^{-4}}\)
- إجابة
-
- \(q^{7}\)
- 16
لنفترض الآن أن لدينا كسرًا مرفوعًا إلى أس سالب. دعونا نستخدم تعريفنا للدعائم السالبة لتقودنا إلى خاصية جديدة.
\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)
للانتقال من الكسر الأصلي المرفوع إلى الأس السالب إلى النتيجة النهائية، أخذنا مقلوب القاعدة - الكسر - وقمنا بتغيير علامة الأس.
هذا يقودنا إلى حاصل القسمة إلى خاصية القوة السالبة.
إذا كانت\(a\)\(b\) الأرقام حقيقية،\(a \neq 0, b \neq 0,\) وكانت عددًا\(n\) صحيحًا، إذن\(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)
قم بالتبسيط:
- \(\left(\dfrac{5}{7}\right)^{-2}\)
- \(\left(-\dfrac{2 x}{y}\right)^{-3}\)
- إجابة
-
- \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
- \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)
قم بالتبسيط:
- \(\left(\dfrac{2}{3}\right)^{-4}\)
- \(\left(-\dfrac{6 m}{n}\right)^{-2}\)
- إجابة
-
- \(\dfrac{81}{16} \)
- \(\dfrac{n^{2}}{36 m^{2}}\)
قم بالتبسيط:
- \(\left(\dfrac{3}{5}\right)^{-3}\)
- \(\left(-\dfrac{a}{2 b}\right)^{-4}\)
- إجابة
-
- \(\dfrac{125}{27}\)
- \(\dfrac{16 b^{4}}{a^{4}}\)
عند تبسيط تعبير يحتوي على أسس، يجب أن نكون حريصين على تحديد القاعدة بشكل صحيح.
قم بالتبسيط:
- \((-3)^{-2}\)
- \(-3^{-2}\)
- \(\left(-\dfrac{1}{3}\right)^{-2}\)
- \(-\left(\dfrac{1}{3}\right)^{-2}\)
- إجابة
-
- هنا ينطبق الأس على القاعدة −3. \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
- \(-3^{-2}\)يعني التعبير «ابحث عن عكس\(3^{-2}\)». هنا ينطبق الأس على الأساس 3. \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
- هنا ينطبق الأس على القاعدة\(\left(-\dfrac{1}{3}\right)\). \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
- \(-\left(\dfrac{1}{3}\right)^{-2}\)يعني التعبير «ابحث عن عكس\(\left(\dfrac{1}{3}\right)^{-2}\)». هنا ينطبق الأس على القاعدة\(\left(\dfrac{1}{3}\right)\). \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)
قم بالتبسيط:
- \((-5)^{-2}\)
- \(-5^{-2}\)
- \(\left(-\dfrac{1}{5}\right)^{-2}\)
- \(-\left(\dfrac{1}{5}\right)^{-2}\)
- إجابة
-
- \(\dfrac{1}{25}\)
- \(-\dfrac{1}{25}\)
- 25
- −25
قم بالتبسيط:
- \((-7)^{-2}\)
- \(-7^{-2}\)
- \(\left(-\dfrac{1}{7}\right)^{-2}\)
- \(-\left(\dfrac{1}{7}\right)^{-2}\)
- إجابة
-
- \(\dfrac{1}{49}\)
- \(-\dfrac{1}{49}\)
- 49
- −49
يجب أن نكون حريصين على اتباع ترتيب العمليات. في المثال التالي، تبدو الأجزاء (أ) و (ب) متشابهة، ولكن النتائج مختلفة.
قم بالتبسيط:
- 4\(\cdot 2^{-1}\)
- \((4 \cdot 2)^{-1}\)
- إجابة
-
- \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
- \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)
قم بالتبسيط:
- 6\(\cdot 3^{-1}\)
- \((6 \cdot 3)^{-1}\)
- إجابة
-
- 2
- \(\dfrac{1}{18}\)
قم بالتبسيط:
- 8\(\cdot 2^{-2}\)
- \((8 \cdot 2)^{-2}\)
- إجابة
-
- 2
- \(\dfrac{1}{256}\)
عندما يتم رفع متغير إلى أس سالب، نطبق التعريف بنفس الطريقة التي قمنا بها مع الأرقام. سنفترض أن جميع المتغيرات غير صفرية.
قم بالتبسيط:
- \(x^{-6}\)
- \(\left(u^{4}\right)^{-3}\)
- إجابة
-
- \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
- \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)
قم بالتبسيط:
- \(y^{-7}\)
- \(\left(z^{3}\right)^{-5}\)
- إجابة
-
- \(\dfrac{1}{y^{7}}\)
- \(\dfrac{1}{z^{15}}\)
قم بالتبسيط:
- \(p^{-9}\)
- \(\left(q^{4}\right)^{-6}\)
- إجابة
-
- \(\dfrac{1}{p^{9}}\)
- \(\dfrac{1}{q^{24}}\)
عندما يكون هناك منتج وأس، يجب أن نكون حريصين على تطبيق الأس على الكمية الصحيحة. وفقًا لترتيب العمليات، نقوم بتبسيط التعبيرات بين قوسين قبل تطبيق الأسس. سنرى كيف يعمل هذا في المثال التالي.
قم بالتبسيط:
- 5\(y^{-1}\)
- \((5 y)^{-1}\)
- \((-5 y)^{-1}\)
- إجابة
-
- \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
- \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
- \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)
قم بالتبسيط:
- 8\(p^{-1}\)
- \((8 p)^{-1}\)
- \((-8 p)^{-1}\)
- إجابة
-
- \(\dfrac{8}{p}\)
- \(\dfrac{1}{8 p}\)
- \(-\dfrac{1}{8 p}\)
قم بالتبسيط:
- 11\(q^{-1}\)
- \((11 q)^{-1}-(11 q)^{-1}\)
- \((-11 q)^{-1}\)
- إجابة
-
- \(\dfrac{11}{1 q}\)
- \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
- \(-\dfrac{1}{11 q}\)
في حالة الأسس السالبة، تحتاج قاعدة حاصل القسمة إلى نموذج واحد فقط\(\dfrac{a^{m}}{a^{n}}=a^{m-n},\) لـ\(a \neq 0\) 0. عندما يكون الأس في المقام أكبر من الأس في البسط، يكون أس القسمة سالبًا.
قم بتبسيط التعبيرات باستخدام أسس عددية
تنطبق جميع خصائص الأس التي قمنا بتطويرها سابقًا في الفصل الذي يحتوي على أسس عددية كاملة على الأسس الصحيحة أيضًا. نعيد ذكرها هنا كمرجع.
إذا كانت\(a\)\(b\) الأرقام حقيقية\(m\) وما زالت أعدادًا\(n\) صحيحة، إذن
\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)
قم بالتبسيط:
- \(x^{-4} \cdot x^{6}\)
- \(y^{-6} \cdot y^{4}\)
- \(z^{-5} \cdot z^{-3}\)
- إجابة
-
- \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
- \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
- \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)
قم بالتبسيط:
- \(x^{-3} \cdot x^{7}\)
- \(y^{-7} \cdot y^{2}\)
- \(z^{-4} \cdot z^{-5}\)
- إجابة
-
- \(x^{4}\)
- \(\dfrac{1}{y^{5}}\)
- \(\dfrac{1}{z^{9}}\)
قم بالتبسيط:
- \(a^{-1} \cdot a^{6}\)
- \(b^{-8} \cdot b^{4}\)
- \(c^{-8} \cdot c^{-7}\)
- إجابة
-
- \(a^{5}\)
- \(\dfrac{1}{b^{4}}\)
- \(\dfrac{1}{c^{15}}\)
في المثالين التاليين، سنبدأ باستخدام خاصية الإبدال لتجميع نفس المتغيرات معًا. هذا يجعل من السهل تحديد القواعد المتشابهة قبل استخدام خاصية المنتج.
قم بالتبسيط:\(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)
- إجابة
-
\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)
قم بالتبسيط:\(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)
- إجابة
-
\(\frac{1}{p^3 q^3}\)
قم بالتبسيط:\(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)
- إجابة
-
\(\frac{1}{r^2 s^8}\)
إذا كانت القيم الأحادية لها معاملات عددية، فإننا نضرب المعاملات، تمامًا كما فعلنا سابقًا.
قم بالتبسيط:\(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)
- إجابة
-
\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)
قم بالتبسيط:\(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)
- إجابة
-
\(-\frac{12v^5}{u}\)
قم بالتبسيط:\(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)
- إجابة
-
\(\frac{30d^3}{c^8}\)
في المثالين التاليين، سنستخدم خاصية الطاقة والمنتج إلى خاصية الطاقة.
قم بالتبسيط:\(\left(6 k^{3}\right)^{-2}\)
- إجابة
-
\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)
قم بالتبسيط:\(\left(-4 x^{4}\right)^{-2}\)
- إجابة
-
\(\frac{1}{16x^8}\)
قم بالتبسيط:\(\left(2 b^{3}\right)^{-4}\)
- إجابة
-
\(\frac{1}{16b^{12}}\)
قم بالتبسيط:\(\left(5 x^{-3}\right)^{2}\)
- إجابة
-
\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)
قم بالتبسيط:\(\left(8 a^{-4}\right)^{2}\)
- إجابة
-
\(\frac{64}{a^8}\)
قم بالتبسيط:\(\left(2 c^{-4}\right)^{3}\)
- إجابة
-
\(\frac{8}{c^{12}}\)
لتبسيط الكسر، نستخدم خاصية حاصل القسمة ونطرح الأسس.
قم بالتبسيط:\(\dfrac{r^{5}}{r^{-4}}\)
- إجابة
-
\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)
قم بالتبسيط:\(\dfrac{x^{8}}{x^{-3}}\)
- إجابة
-
\(x^{11}\)
قم بالتبسيط:\(\dfrac{y^{8}}{y^{-6}}\)
- إجابة
-
\(y^{14}\)
التحويل من الترميز العشري إلى الترميز العلمي
هل تتذكر العمل باستخدام القيمة المكانية للأرقام الصحيحة والأرقام العشرية؟ يعتمد نظام الأرقام لدينا على قوى 10. نحن نستخدم العشرات والمئات والآلاف وما إلى ذلك. تعتمد أعدادنا العشرية أيضًا على قوى العشرات - الأجزاء من عشرة والأجزاء من مائة والأجزاء من ألف وما إلى ذلك. ضع في اعتبارك الأرقام 4,000 و 0.004. نحن نعلم أن 4000 تعني\(4 \times 1,000\) و 0.004 تعني\(4 \times \dfrac{1}{1,000}\).
إذا كتبنا 1000 في صورة قوة عشرة في الصورة الأسية، يمكننا إعادة كتابة هذه الأعداد بهذه الطريقة:
\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]
عندما تتم كتابة رقم كناتج لعددين، حيث يكون العامل الأول عددًا أكبر من أو يساوي واحدًا ولكنه أقل من 10، والعامل الثاني هو قوة 10 مكتوبة في الصورة الأسية، يُقال أنه في الترميز العلمي.
يتم التعبير عن الرقم بالتدوين العلمي عندما يكون بالشكل
\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]
من المعتاد في الترميز العلمي استخدام علامة\(\times\) الضرب، على الرغم من أننا نتجنب استخدام هذه العلامة في مكان آخر في الجبر.
إذا نظرنا إلى ما حدث للفاصلة العشرية، يمكننا أن نرى طريقة للتحويل بسهولة من الترميز العشري إلى الترميز العلمي.
في كلتا الحالتين، تم نقل الرقم العشري إلى 3 أماكن للحصول على العامل الأول بين 1 و10.
\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)
اكتب بالتدوين العلمي: 37000.
- إجابة
-
اكتب بالتدوين العلمي: 96000.
- إجابة
-
\(9.6 \times 10^{4}\)
اكتب بالتدوين العلمي: 48300.
- إجابة
-
\(4.83 \times 10^{4}\)
- الخطوة 1. انقل الفاصلة العشرية بحيث يكون العامل الأول أكبر من أو يساوي 1 ولكن أقل من 10.
- الخطوة 2. احسب عدد المنازل العشرية، n، التي تم نقل العلامة العشرية إليها.
- الخطوة 3. اكتب الرقم في صورة منتج بقوة ١٠.
إذا كان الرقم الأصلي هو:- أكبر من 1، ستكون قوة 10 نيوتن.
- بين 0 و1، ستكون قوة العدد 10 10 −n.
- الخطوة 4. تحقق.
اكتب بالتدوين العلمي: 0.0052.
- إجابة
-
الرقم الأصلي، 0.0052، يقع بين 0 و 1، لذا ستكون لدينا قوة سالبة قدرها 10.
انقل النقطة العشرية للحصول على 5.2، وهو رقم بين 1 و10. احسب عدد المنازل العشرية التي تم نقل النقطة إليها. اكتب كمنتج بقوة 10. تحقق. \(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\) 0.0052
اكتب بالتدوين العلمي: 0.0078
- إجابة
-
\(7.8 \times 10^{-3}\)
اكتب بالتدوين العلمي: 0.0129
- إجابة
-
\(1.29 \times 10^{-2}\)
تحويل الترميز العلمي إلى الصورة العشرية
كيف يمكننا التحويل من الترميز العلمي إلى الشكل العشري؟ دعونا ننظر إلى رقمين مكتوبين بالتدوين العلمي ونرى.
\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]
إذا نظرنا إلى موقع النقطة العشرية، يمكننا أن نرى طريقة سهلة لتحويل رقم من الترميز العلمي إلى الشكل العشري.
\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]
في كلتا الحالتين، انتقلت النقطة العشرية إلى 4 أماكن. عندما كان الأس موجبًا، انتقل الرقم العشري إلى اليمين. عندما كان الأس سالبًا، انتقلت العلامة العشرية إلى اليسار.
تحويل إلى نموذج عشري:\(6.2 \times 10^{3}\)
- إجابة
-
تحويل إلى نموذج عشري:\(1.3 \times 10^{3}\)
- إجابة
-
\(1,300\)
تحويل إلى نموذج عشري:\(9.25 \times 10^{4}\)
- إجابة
-
\(92,500\)
يتم تلخيص الخطوات أدناه.
تحويل الترميز العلمي إلى صيغة عشرية.
لتحويل الترميز العلمي إلى الشكل العشري:
- الخطوة 1. حدد الأس\(n\)، على العامل\(10\).
- الخطوة 2. انقل المنازل\(n\) العشرية مع إضافة الأصفار إذا لزم الأمر.
- إذا كان الأس موجبًا، انقل منازل النقاط\(n\) العشرية إلى اليمين.
- إذا كان الأس سالبًا، انقل منازل النقاط\(|n|\) العشرية إلى اليسار.
- الخطوة 3. تحقق.
تحويل إلى نموذج عشري:\(8.9\times 10^{-2}\)
- إجابة
-
حدد الأس\(n\)، على العامل\(10\). بما أن الأس سالب، انقل العلامة العشرية منزلتين إلى اليسار. أضف الأصفار حسب الحاجة للعناصر النائبة.
تحويل إلى نموذج عشري:\(1.2 \times 10^{-4}\)
- إجابة
-
\(0.00012\)
تحويل إلى نموذج عشري:\(7.5 \times 10^{-2}\)
- إجابة
-
\(0.075\)
الضرب والقسمة باستخدام الترميز العلمي
يستخدم علماء الفلك أعدادًا كبيرة جدًا لوصف المسافات في الكون وأعمار النجوم والكواكب. يستخدم الكيميائيون أعدادًا صغيرة جدًا لوصف حجم الذرة أو الشحنة على الإلكترون. عندما يقوم العلماء بإجراء حسابات بأعداد كبيرة جدًا أو صغيرة جدًا، فإنهم يستخدمون الترميز العلمي. يوفر الترميز العلمي طريقة لإجراء العمليات الحسابية دون كتابة الكثير من الأصفار. سنرى كيف يتم استخدام خصائص الأسس لضرب الأرقام وقسمتها في الترميز العلمي.
اضرب. اكتب الإجابات في شكل عشري:\(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)
- إجابة
-
\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)
اضرب\((3\times 10^{6})(2\times 10^{-8})\). اكتب الإجابات بصيغة عشرية.
- إجابة
-
\(0.06\)
اضرب\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\). اكتب الإجابات بصيغة عشرية.
- إجابة
-
\(0.009\)
يقسم. اكتب الإجابات في شكل عشري:\(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)
- إجابة
-
\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)
اقسم\(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\) اكتب الإجابات في صورة عشرية.
- إجابة
-
\(400,000\)
اقسم\(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\) اكتب الإجابات في صورة عشرية.
- إجابة
-
\(20,000\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الأسس الصحيحة والرموز العلمية:
- أسس سالبة
- الترميز العلمي
- الترميز العلمي 2
المفاهيم الرئيسية
- خاصية الأسس السالبة
- إذا كان\(n\) عددًا صحيحًا موجبًا\(a \ne 0\)، ثم\(\dfrac{1}{a^{−n}}=a^n\)
- إذا كان\(n\) عددًا صحيحًا موجبًا\(a \ne 0\)، ثم\(\dfrac{1}{a^{−n}}=a^n\)
- حاصل القسمة على الأس السالب
- إذا كانت\(a\)\(b\) الأرقام حقيقية،\(b \ne 0\) وكانت عددًا\(n\) صحيحًا، إذن\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- إذا كانت\(a\)\(b\) الأرقام حقيقية،\(b \ne 0\) وكانت عددًا\(n\) صحيحًا، إذن\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- لتحويل الترميز العلمي إلى الشكل العشري:
- حدد الأس،\(n\) على العامل\(10\).
- انقل المنازل\(n\) العشرية مع إضافة الأصفار إذا لزم الأمر.
- إذا كان الأس موجبًا، انقل منازل النقاط\(n\) العشرية إلى اليمين.
- إذا كان الأس سالبًا، انقل منازل النقاط\(|n|\) العشرية إلى اليسار.
- تحقق.
- لتحويل رقم عشري إلى ترميز علمي:
- انقل الفاصلة العشرية بحيث يكون العامل الأول أكبر من أو يساوي\(1\) ولكن أقل من\(10\).
- احسب عدد المنازل العشرية\(n\) التي تم نقل العلامة العشرية إليها.
- اكتب الرقم كمنتج بقوة\(10\). إذا كان الرقم الأصلي هو:
- أكبر\(1\) من قوة\(10\) الإرادة\(10^n\)
- بين\(0\) و\(1\)، قوة\(10\) الإرادة\(10^{−n}\)
- تحقق.
مسرد المصطلحات
- أس سالب
- إذا كان\(n\) عددًا صحيحًا موجبًا\(a \neq 0\)، ثم\(a^{-n}=\dfrac{1}{a^{n}}\).
- الترميز العلمي
- يتم التعبير عن الرقم بالتدوين العلمي عندما يكون بالشكل\(a \times 10^{n}\) حيث\(a \geq 1\) و<10\(n\) ويكون عددًا صحيحًا.


