Skip to main content
Global

5.4: حل التطبيقات باستخدام أنظمة المعادلات

  1. Last updated
  2. Save as PDF
  • Page ID
    200152

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • ترجم إلى نظام المعادلات
    • حل تطبيقات الترجمة المباشرة
    • حل تطبيقات الهندسة
    • حل تطبيقات الحركة الموحدة
    ملاحظة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. مجموع ضعف العدد وتسعة يساوي 31. ابحث عن الرقم.
      إذا فاتتك هذه المشكلة، راجع التمرين 3.1.10.
    2. حصل التوأم جون ورون معًا على 96,000 دولار العام الماضي. حصل رون على 8000 دولار أكثر من ثلاثة أضعاف ما حصل عليه جون. كم كسب كل من التوائم؟
      إذا فاتتك هذه المشكلة، راجع التمرين 3.1.31.
    3. يركب أليسيو\(3\frac{1}{2}\) ساعات دراجته بمعدل 10 أميال في الساعة. إلى أي مدى ركب؟
      إذا فاتتك هذه المشكلة، راجع التمرين 2.6.1.

    في السابق في هذا الفصل، قمنا بحل العديد من التطبيقات باستخدام أنظمة المعادلات الخطية. في هذا القسم، سنلقي نظرة على بعض الأنواع المحددة من التطبيقات التي تربط كميتين. سنترجم الكلمات إلى معادلات خطية، ونقرر الطريقة الأكثر ملاءمة للاستخدام، ثم نحلها.

    سنستخدم إستراتيجية حل المشكلات الخاصة بنا لأنظمة المعادلات الخطية.

    استخدم استراتيجية حل المشكلات لأنظمة المعادلات الخطية.

    1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
    2. حدد ما نبحث عنه.
    3. اذكر ما نبحث عنه. اختر المتغيرات لتمثيل تلك الكميات.
    4. ترجم إلى نظام من المعادلات.
    5. حل نظام المعادلات باستخدام تقنيات الجبر الجيدة.
    6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
    7. أجب على السؤال بجملة كاملة.

    ترجمة إلى نظام المعادلات

    ترتبط العديد من المشكلات التي قمنا بحلها في التطبيقات السابقة بكميتين. فيما يلي مثالان من الفصل الخاص بنماذج الرياضيات.

    • مجموع رقمين هو سالب أربعة عشر. رقم واحد أقل بأربعة من الآخر. ابحث عن الأرقام.
    • يكسب الزوجان معًا 110,000 دولار سنويًا. تكسب الزوجة 16 ألف دولار أقل من ضعف ما يكسبه زوجها. ماذا يكسب الزوج؟

    في هذا الفصل، قمنا بترجمة كل موقف إلى معادلة واحدة باستخدام متغير واحد فقط. في بعض الأحيان كان الأمر صعبًا بعض الشيء في معرفة كيفية تسمية الكميتين، أليس كذلك؟

    دعونا نرى كيف يمكننا ترجمة هاتين المشكلتين إلى نظام معادلات بمتغيرين. سنركز على الخطوات من 1 إلى 4 من إستراتيجية حل المشكلات الخاصة بنا.

    التمارين\(\PageIndex{1}\): How to Translate to a System of Equations

    ترجم إلى نظام المعادلات:

    مجموع رقمين هو سالب أربعة عشر. رقم واحد أقل بأربعة من الآخر. ابحث عن الأرقام.

    إجابة

    يحتوي هذا الشكل على أربعة صفوف وثلاثة أعمدة. يقرأ الصف الأول، «الخطوة 1: اقرأ المشكلة. تأكد من أنك تفهم كل الكلمات والأفكار. هذه مشكلة عددية. مجموع رقمين هو سالب أربعة عشر. رقم واحد أقل بأربعة من الآخر. ابحث عن الأرقام.»يقرأ الصف الثاني، «الخطوة 2: حدد ما تبحث عنه. «ابحث عن الأرقام.» نحن نبحث عن رقمين.»يقرأ الصف الثالث، «الخطوة 3: قم بتسمية ما تبحث عنه. اختر المتغيرات لتمثيل تلك الكميات. سنستخدم متغيرين، m و n. دعني = رقم واحد n = الرقم الثاني.»يقرأ الصف الرابع، «الخطوة 4: ترجم إلى نظام المعادلات. سنكتب معادلة واحدة لكل جملة.» يوضح الشكل بعد ذلك كيف يصبح «مجموع الأرقام هو -14" m + n = -14 و «رقم واحد أقل بأربعة من الآخر» يصبح m = n - 4. ثم يقول الشكل: «النظام هو m + n = -14 و m = n - 4.»

    التمارين\(\PageIndex{2}\)

    ترجم إلى نظام المعادلات:

    مجموع رقمين هو سالب ثلاثة وعشرين. رقم واحد أقل بـ 7 من الآخر. ابحث عن الأرقام.

    إجابة

    \(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)

    التمارين\(\PageIndex{3}\)

    ترجم إلى نظام المعادلات:

    مجموع عددين هو سالب ثمانية عشر. رقم واحد يزيد بمقدار 40 عن الآخر. ابحث عن الأرقام.

    إجابة

    \(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)

    سنقوم بمثال آخر حيث نتوقف بعد كتابة نظام المعادلات.

    التمارين\(\PageIndex{4}\)

    ترجم إلى نظام المعادلات:

    يكسب الزوجان معًا 110,000 دولار سنويًا. تكسب الزوجة 16 ألف دولار أقل من ضعف ما يكسبه زوجها. ماذا يكسب الزوج؟

    إجابة

    \(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)

    التمارين\(\PageIndex{5}\)

    ترجم إلى نظام المعادلات:

    يبلغ إجمالي دخل الأسرة للزوجين 84,000 دولار. يكسب الزوج 18 ألف دولار أقل من ضعف ما تكسبه الزوجة. كم تكسب الزوجة؟

    إجابة

    \(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)

    التمارين\(\PageIndex{6}\)

    ترجم إلى نظام المعادلات:

    يكسب الموظف الكبير 5 دولارات أقل من ضعف ما يجنيه الموظف الجديد في الساعة. يجنون معًا 43 دولارًا في الساعة. كم يكسب كل موظف في الساعة؟

    إجابة

    \(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)

    حل تطبيقات الترجمة المباشرة

    قمنا بإعداد أنظمة المعادلات في التمرين\(\PageIndex{1}\) والتمرين ولكننا لم نحلها\(\PageIndex{4}\) الآن سنترجم الموقف إلى نظام معادلات ثم نحله.

    التمارين\(\PageIndex{7}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    ديفون أكبر بـ 26 عامًا من ابنه كوبر. مجموع أعمارهم هو 50. ابحث عن أعمارهم.

    إجابة
    الخطوة 1. اقرأ المشكلة.  
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن أعمار ديفون وكوبر.
    الخطوة 3. اذكر ما نبحث عنه. دعونا d= عمر ديفون.
    c= عمر كوبر
    الخطوة 4. ترجم إلى نظام من المعادلات. ديفون أكبر من كوبر بـ 26 عامًا.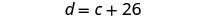
      .
      مجموع أعمارهم هو 50.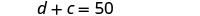
      .
    النظام هو: .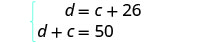
    الخطوة 5. حل نظام المعادلات.

    حل عن طريق الاستبدال.    		 .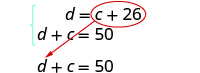
    استبدل c + 26 في المعادلة الثانية. .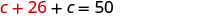
    حل لـ ج. .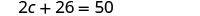
      .
      .
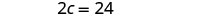
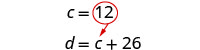
    استبدل c = 12 في المعادلة الأولى ثم قم بحل d. .
      .
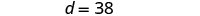
    الخطوة 6. تحقق من الإجابة في المشكلة. هل عمر ديفون 26 أكثر من عمر كوبر؟
    نعم، 38 يزيد بمقدار 26 عن 12.
    هل مجموع أعمارهم 50؟
    نعم، 38 زائد 12 يساوي 50.
    الخطوة 7. أجب على السؤال. ديفون تبلغ من العمر 38 عامًا وكوبر تبلغ من العمر 12 عامًا.
    التمارين\(\PageIndex{8}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    علي أكبر بـ 12 عامًا من أخته الصغرى جميلة. مجموع أعمارهم هو 40. ابحث عن أعمارهم.

    إجابة

    علي تبلغ من العمر 26 عامًا وجميلة تبلغ من العمر 14 عامًا.

    التمارين\(\PageIndex{9}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    يبلغ عمر والد جيك 6 مرات أكثر من 3 أضعاف عمر جيك. مجموع أعمارهم هو 42. ابحث عن أعمارهم.

    إجابة

    جيك يبلغ من العمر 9 سنوات ووالده يبلغ من العمر 33 عامًا.

    التمارين\(\PageIndex{10}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    عندما أمضت جينا 10 دقائق على المدرب البيضاوي ثم أجرت تدريبات دائرية لمدة 20 دقيقة، يقول تطبيق اللياقة البدنية الخاص بها إنها أحرقت 278 سعرة حرارية. عندما أمضت 20 دقيقة في التدريب الإهليلجي و30 دقيقة من التدريب الدائري، أحرقت 473 سعرة حرارية. كم عدد السعرات الحرارية التي تحرقها في كل دقيقة على جهاز التدريب الإهليلجي؟ كم عدد السعرات الحرارية التي تحرقها في كل دقيقة من التدريب الدائري؟

    إجابة
    الخطوة 1. اقرأ المشكلة.  
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن عدد
    السعرات الحرارية المحروقة كل دقيقة على جهاز التدريب
    الإهليلجي وكل دقيقة من
    التدريب الدائري.
    الخطوة 3. اذكر ما نبحث عنه. دع e= عدد السعرات الحرارية المحروقة في الدقيقة على جهاز التدريب الإهليلجي.
    c = عدد السعرات الحرارية المحروقة في الدقيقة أثناء التدريب الدائري
    الخطوة 4. ترجم إلى نظام من المعادلات. 10 دقائق من التدريب البيضاوي
    والتدريب الدائري لمدة 20 دقيقة، وحرق
    278 سعرة حرارية
      .
      20 دقيقة على جهاز بيضاوي و
    30 دقيقة من التدريب الدائري أحرقت
    473 سعرة حرارية
      .
    النظام هو: .
    الخطوة 5. حل نظام المعادلات.  
    اضرب المعادلة الأولى في −2 للحصول على معاملات عكسية لـ e. .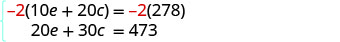
    قم بتبسيط المعادلات وإضافتها.

    حل لـ ج.    		 .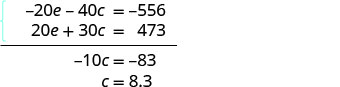
    استبدل c = 8.3 في إحدى المعادلات الأصلية لحلها لـ e. .
      .
      .
      .
      .
    الخطوة 6. تحقق من الإجابة في المشكلة. تحقق من الرياضيات بنفسك.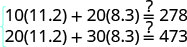
    .  
    الخطوة 7. أجب على السؤال. تحرق جينا 8.3 سعرة حرارية في الدقيقة من
    التدريب الدائري و11.2 سعرة حرارية في
    الدقيقة أثناء استخدام جهاز التدريب الإهليلجي.
    التمارين\(\PageIndex{11}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    ذهب مارك إلى صالة الألعاب الرياضية ومارس 40 دقيقة من اليوغا الساخنة من بيكرام و 10 دقائق من القفز. لقد أحرق 510 سعرة حرارية. في المرة التالية التي ذهب فيها إلى صالة الألعاب الرياضية، مارس اليوجا الساخنة لمدة 30 دقيقة من بيكرام و 20 دقيقة من القفز على الرافعات التي تحرق 470 سعرة حرارية. كم عدد السعرات الحرارية التي تم حرقها لكل دقيقة من اليوجا؟ كم عدد السعرات الحرارية التي تم حرقها لكل دقيقة من القفز؟

    إجابة

    أحرق مارك 11 سعرًا حراريًا لكل دقيقة من اليوجا و 7 سعرات حرارية لكل دقيقة من القفز.

    التمارين\(\PageIndex{12}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    أمضت إيرين 30 دقيقة على آلة التجديف و 20 دقيقة في رفع الأثقال في صالة الألعاب الرياضية وحرقت 430 سعرة حرارية. خلال زيارتها التالية إلى صالة الألعاب الرياضية، أمضت 50 دقيقة على آلة التجديف و10 دقائق في رفع الأثقال وحرق 600 سعرة حرارية. كم عدد السعرات الحرارية التي أحرقتها لكل دقيقة على جهاز التجديف؟ كم عدد السعرات الحرارية التي أحرقتها في كل دقيقة من رفع الأثقال؟

    إجابة

    أحرقت إيرين 11 سعرًا حراريًا لكل دقيقة على جهاز التجديف و 5 سعرات حرارية لكل دقيقة من رفع الأثقال.

    حل تطبيقات الهندسة

    عندما تعلمنا عن نماذج الرياضيات، قمنا بحل تطبيقات الهندسة باستخدام خصائص المثلثات والمستطيلات. الآن سنضيف إلى قائمتنا بعض خصائص الزوايا.

    تصل قياسات الزاويتين المتكاملتين إلى 90 درجة. تصل قياسات الزاويتين التكميليتين إلى 180 درجة.

    الزوايا التكميلية والتكميلية

    تتكامل زاويتان إذا كان مجموع قياسات زواياهما 90 درجة.

    تكون زاويتان متكاملتان إذا كان مجموع قياسات زواياهما 180 درجة.

    إذا كانت زاويتان متكاملتان، فإننا نقول إن إحدى الزوايا تكمل الأخرى.

    إذا كانت زاويتان متكاملتان، فإننا نقول إن إحدى الزوايا تكمل الأخرى.

    التمارين\(\PageIndex{13}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    الفرق بين زاويتين متكاملتين هو 26 درجة. أوجد قياسات الزوايا.

    إجابة

    \(\begin{array}{ll}{\textbf {Step 1. Read}\text{ the problem. }} & {} \\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} & {\text {We are looking for the measure of each angle.}} \\ \\ {\textbf{Step 3. Name}\text{ what we are looking for.}} & {\text{Let x = the measure of the first angle.} }\\ {} & \text{y = the measure of the second angle} \\ \textbf{Step 4. Translate}\text{ into a system of equations.}& \text{The angles are complementary.} \\ & \text{x+y=90} \\ & \text{The difference of the two angles is 26 degrees.} \\ & \text{x−y=26} \\ \\ \text{The system is} & {\left\{\begin{array}{l}{x+y=90} \\ {x-y=26}\end{array}\right.} \\ \textbf{Step 5. Solve}\text{ the system of equations by elimination.} \\& \left\{\begin{array}{l}{x+y=90} \\ \underline{x-y=26}\end{array}\right. \\ & \quad2x\quad=116 \\ \text{Substitute x = 58 into the first equation.}& \begin{array}{lrll} &x&=&58 \\ &x+y&=&90 \\ &58+y&=&90 \\ &y&=&32\end{array} \\ \textbf{Step 6. Check}\text{ the answer in the problem.} & \\ 58+32=90\checkmark\\ 58-32=36\checkmark \\ \\ \textbf{Step 7. Answer}\text{ the question.} & \text{The angle measures are 58 degrees and 32 degrees.}\end{array}\)

    التمارين\(\PageIndex{14}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    الفرق بين زاويتين متكاملتين هو 20 درجة. أوجد قياسات الزوايا.

    إجابة

    قياسات الزاوية هي 55 درجة و 35 درجة.

    التمارين\(\PageIndex{15}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    الفرق بين زاويتين متكاملتين هو 80 درجة. أوجد قياسات الزوايا.

    إجابة

    قياسات الزاوية هي 5 درجات و 85 درجة.

    التمارين\(\PageIndex{16}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    زاويتان مكملتان. قياس الزاوية الأكبر أقل باثني عشر درجة من خمسة أضعاف قياس الزاوية الأصغر. أوجد قياسات كلتا الزاويتين.

    إجابة
    الخطوة 1. اقرأ المشكلة.  
    الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن قياس كل زاوية.
    الخطوة 3. اذكر ما نبحث عنه. دع x = قياس الزاوية الأولى.
    y = قياس الزاوية الثانية
    الخطوة 4. ترجم إلى نظام من المعادلات. الزوايا تكميلية.
      .
      الزاوية الأكبر تقل بمقدار اثني عشر عن خمسة أضعاف الزاوية الأصغر
      .
    النظام هو:


    الخطوة 5. حل نظام استبدال المعادلات.    		 .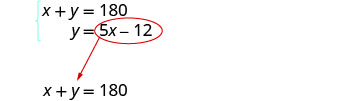
    استبدل ٥ x − ١٢ عن y في المعادلة الأولى. .
    حل لـ x. .
      .
      .
    استبدل 32 في المعادلة الثانية، ثم حل لـ y. .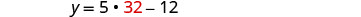
      .
      .
    الخطوة 6. تحقق من الإجابة في المشكلة.

    \(\begin{aligned} 32+158 &=180 \checkmark \\ 5 \cdot 32-12 &=147 \checkmark \end{aligned}\)    		  
    الخطوة 7. أجب على السؤال. مقاييس الزاوية هي 148 و 32.
    التمارين\(\PageIndex{17}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    زاويتان مكملتان. قياس الزاوية الأكبر يزيد بمقدار 12 درجة عن ثلاثة أضعاف الزاوية الأصغر. أوجد قياسات الزوايا.

    إجابة

    قياسات الزاوية هي 42 درجة و 138 درجة.

    التمارين\(\PageIndex{18}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    زاويتان مكملتان. قياس الزاوية الأكبر يقل بمقدار 18 عن ضعف قياس الزاوية الأصغر. أوجد قياسات الزوايا.

    إجابة

    قياسات الزاوية هي 66 درجة و 114 درجة.

    التمارين\(\PageIndex{19}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    يمتلك راندال سياجًا بطول 125 قدمًا لإحاطة الجزء المستطيل من الفناء الخلفي لمنزله المجاور لمنزله. سيحتاج فقط إلى السياج حول ثلاثة جوانب، لأن الجانب الرابع سيكون جدار المنزل. يريد أن يكون طول الفناء المسور (الموازي لجدار المنزل) 5 أقدام أكثر من أربعة أضعاف العرض. ابحث عن الطول والعرض.

    إجابة
    الخطوة 1. اقرأ المشكلة.  
    الخطوة 2. حدد ما تبحث عنه. نحن نبحث عن الطول والعرض.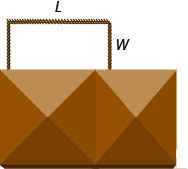
      .
    الخطوة 3. اذكر ما نبحث عنه. دع L = طول الفناء المسور.
    W = عرض الفناء المسورة
    الخطوة 4. ترجم إلى نظام من المعادلات. طول واحد وعرضان يساويان 125.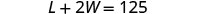
      .
      سيكون الطول 5 أقدام أكثر من أربعة أضعاف العرض.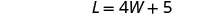
      .
    النظام هو:

    الخطوة 5. حل نظام المعادلات عن طريق الاستبدال.    		 .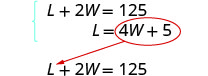
    استبدل L = 4 W + 5 في
    المعادلة الأولى، ثم قم بحل W.    		 .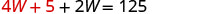
      .
      .
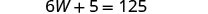
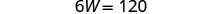
    استبدل 20 بـ W في
    المعادلة الثانية، ثم حل L.    		 .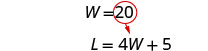
      .
      .
      .
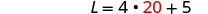
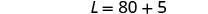
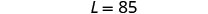
    الخطوة 6. تحقق من الإجابة في المشكلة.

    \(\begin{array}{rll} 20+28+20&=&125\checkmark \\ 85 &=&4\cdot 20 + 5\checkmark\end{array}\)    		  
    الخطوة 7. أجب على المعادلة. الطول 85 قدمًا والعرض 20 قدمًا.
    التمارين\(\PageIndex{20}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    يريد ماريو وضع سياج مستطيل حول المسبح في الفناء الخلفي لمنزله. نظرًا لوجود جانب واحد مجاور للمنزل، فإنه سيحتاج فقط إلى السياج من ثلاثة جوانب. هناك جانبان طويلان والجانب الأقصر موازٍ للمنزل. يحتاج إلى 155 قدمًا من السياج لإحاطة المسبح. يقل طول الجانب الطويل بمقدار 10 أقدام عن ضعف العرض. ابحث عن طول وعرض منطقة حمام السباحة التي سيتم تضمينها.

    إجابة

    الطول 60 قدمًا والعرض 35 قدمًا.

    التمارين\(\PageIndex{21}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    تريد أليكسيس بناء كلب مستطيل يركض في فناء منزلها المجاور لسياج جارتها. سوف تستخدم 136 قدمًا من السياج لإحاطة مسار الكلب المستطيل بالكامل. سيكون طول مسار الكلب على طول سياج الجار أقل بـ 16 قدمًا من ضعف العرض. ابحث عن طول وعرض مسار الكلب.

    إجابة

    الطول 60 قدمًا والعرض 38 قدمًا.

    حل تطبيقات الحركة الموحدة

    استخدمنا جدولًا لتنظيم المعلومات في مشاكل الحركة الموحدة عندما قدمناها مسبقًا. سنواصل استخدام الجدول هنا. كانت المعادلة الأساسية هي D = rt حيث D هي المسافة المقطوعة، r هي المعدل، و t هي الوقت.

    سيكون المثال الأول لتطبيق الحركة الموحدة هو حالة مشابهة لبعض الحالات التي رأيناها بالفعل، ولكن الآن يمكننا استخدام متغيرين ومعادلتين.

    التمارين\(\PageIndex{22}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    غادر جوني سانت لويس على الطريق السريع، متجهًا غربًا نحو دنفر بسرعة 65 ميلًا في الساعة. بعد نصف ساعة، غادر كيلي سانت لويس على نفس طريق جوني، وكان يقود 78 ميلاً في الساعة. كم من الوقت ستستغرق كيلي للحاق بجوني؟

    إجابة

    الرسم التخطيطي مفيد في مساعدتنا على تصور الموقف.

    يوضح هذا الشكل رسمًا بيانيًا. دنفر على اليسار وسانت لويس على اليمين. هناك شعاع يمتد من سانت لويس إلى دنفر. يُطلق عليه اسم «جوني» و «65 مترًا في الساعة». هناك شعاع آخر يمتد من سانت لويس إلى دنفر. يُطلق عليه «كيلي (بعد نصف ساعة)» و «78 مترًا في الساعة».

    حدد ما نبحث عنه وقم بتسميته.
    سيساعدنا المخطط على تنظيم البيانات.
    نحن نعرف معدلات كل من جوني وكيلي، ولذا
    ندخلها في الرسم البياني.    		  
    نحن نبحث عن طول الفترة الزمنية التي سيقودها كل من كيلي،
    ك، وجوني، جيه.
    منذ d=r·t يمكننا ملء عمود المسافة.    		 .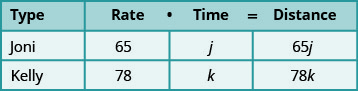
    ترجم إلى نظام من المعادلات.
    لإنشاء نظام المعادلات، يجب أن ندرك أن كيلي وجوني سيقودان نفس المسافة. لذلك، 65 م = 78 كيلو.

    أيضًا، نظرًا لأن كيلي غادرت لاحقًا، سيكون وقتها أقل بـ 12-12 ساعة من وقت جوني.

    إذن، k=j−12.
    الآن لدينا النظام. .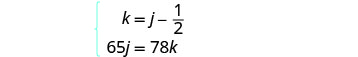
    حل نظام المعادلات عن طريق الاستبدال. .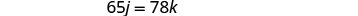
    استبدل k=j−12 في المعادلة الثانية، ثم حل لـ j. .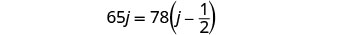
      .
      .
      .
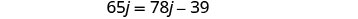
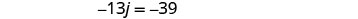
    لإيجاد وقت كيلي، استبدل j = 3 في المعادلة الأولى، ثم قم بحل k. .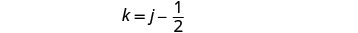
      .
      .
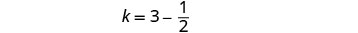
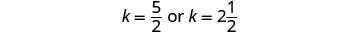
    تحقق من الإجابة في المشكلة.
    انضم لمدة 3 ساعات (65 ميلاً في الساعة) = 195 ميلاً.
    \(2\frac{1}{2}\)ساعات كيلي (78 ميلاً في الساعة) = 195 ميلاً.
    نعم، سيكونون قد قطعوا نفس المسافة
    عندما يلتقون.    		  
    أجب على السؤال. سوف يلحق كيلي بجوني في\(2\frac{1}{2}\) غضون ساعات.
    بحلول ذلك الوقت، ستكون جوني قد سافرت لمدة 3 ساعات.
    التمارين\(\PageIndex{23}\)

    ترجم إلى نظام المعادلات ثم حلها: غادر ميتشل ديترويت على الطريق السريع متجهًا جنوبًا نحو أورلاندو بسرعة 60 ميلاً في الساعة. غادر كلارك ديترويت بعد ساعة مسافراً بسرعة 75 ميلاً في الساعة، متبعًا نفس مسار ميتشل. كم من الوقت سيستغرق كلارك للقبض على ميتشل؟

    إجابة

    سوف يستغرق كلارك 4 ساعات للقبض على ميتشل.

    التمارين\(\PageIndex{24}\)

    ترجم إلى نظام من المعادلات ثم حلها: غادر تشارلي منزل والدته مسافراً بسرعة متوسطة 36 ميلاً في الساعة. غادرت أخته سالي بعد 15 دقيقة (1/4 ساعة) مسافرة في نفس الطريق بمتوسط سرعة 42 ميلاً في الساعة. كم من الوقت قبل أن تلتقي سالي بتشارلي؟

    إجابة

    سوف تستغرق سالي\(1\frac{1}{2}\) ساعات للحاق بتشارلي.

    تنشأ العديد من التطبيقات الواقعية للحركة المنتظمة بسبب تأثيرات التيارات - الماء أو الهواء - على السرعة الفعلية للسيارة. تستغرق رحلات الطائرات عبر البلاد في الولايات المتحدة عمومًا وقتًا أطول من الذهاب غربًا مقارنة بالتوجه شرقًا بسبب تيارات الرياح السائدة.

    دعونا نلقي نظرة على قارب يسافر على النهر. اعتمادًا على الاتجاه الذي يسير فيه القارب، يؤدي تيار الماء إما إلى إبطائه أو تسريعه.

    \(\PageIndex{2}\)يوضح الشكل\(\PageIndex{1}\) والشكل كيف يؤثر تيار النهر على السرعة التي يسير بها القارب بالفعل. سنسمي سرعة القارب في المياه الساكنة b وسرعة تيار النهر c.

    في الشكل\(\PageIndex{1}\)، يتجه القارب في اتجاه مجرى النهر، في نفس اتجاه تيار النهر. يساعد التيار في دفع القارب، وبالتالي تكون السرعة الفعلية للقارب أسرع من سرعته في الماء الساكن. السرعة الفعلية التي يتحرك بها القارب هي b + c.

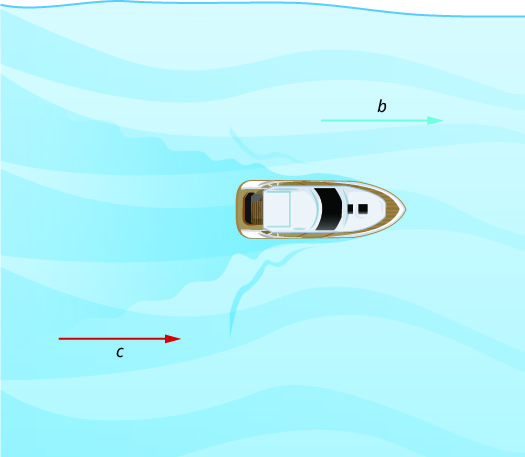
    يوضِّح هذا الشكل قاربًا يطفو في الماء. على اليمين، يوجد سهم يشير إلى القارب. يطلق عليه اسم «c». على اليسار، يوجد سهم يشير بعيدًا عن القارب. يتم تسميته بـ «b».
    الشكل\(\PageIndex{1}\)

    في الشكل\(\PageIndex{2}\)، يتجه القارب نحو المنبع، مقابل تيار النهر. التيار يسير ضد القارب، وبالتالي فإن السرعة الفعلية للقارب أبطأ من سرعته في الماء الساكن. السرعة الفعلية للقارب هي b−c.

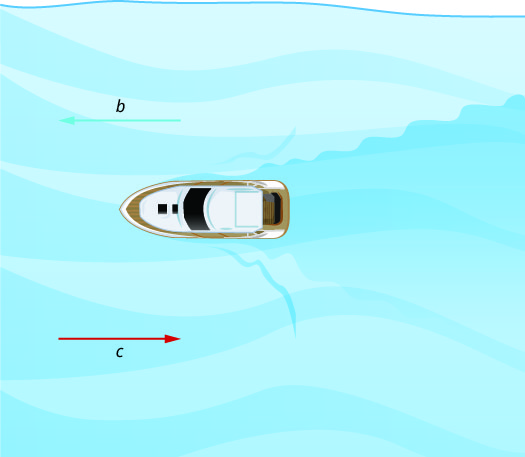
    يوضِّح هذا الشكل قاربًا يطفو في الماء. إلى اليسار يوجد سهم يشير بعيدًا عن القارب المسمى «b»، وسهم يشير إلى القارب المسمى «c».
    الشكل\(\PageIndex{2}\)

    سنضع بعض الأرقام لهذا الموقف في التمرين\(\PageIndex{25}\).

    التمارين\(\PageIndex{25}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    أبحرت سفينة سياحية نهرية 60 ميلًا في اتجاه مجرى النهر لمدة 4 ساعات ثم استغرقت 5 ساعات في الإبحار في اتجاه المنبع للعودة إلى الرصيف. أوجد سرعة السفينة في الماء الساكن وسرعة تيار النهر.

    إجابة

    اقرأ المشكلة.

    هذه مشكلة حركة موحدة وستساعدنا الصورة على تصور الموقف.

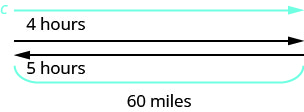
    يوضح هذا الشكل سهمًا يحمل علامة «c» ويستمر إلى اليمين ويمثل الموجة. تحت الموجة يوجد شعاع يشير إلى اليمين ويطلق عليه «أربع ساعات». تحت هذا الشعاع يوجد شعاع آخر يشير إلى اليسار المسمى «خمس ساعات». إنه نفس طول الشعاع المسمى «أربع ساعات». يوجد قوس تحت الشعاع يسمى «خمس ساعات». يُطلق على القوس اسم «60 ميلًا».

    حدد ما نبحث عنه. نحن نبحث عن سرعة السفينة
    في المياه الساكنة وسرعة التيار.
    اذكر ما نبحث عنه. Let s=s= معدل السفينة في الماء الساكن.
    c=c= معدل التيار
    سيساعدنا المخطط على تنظيم المعلومات.
    تتجه السفينة نحو المصب ثم المنبع.
    عند الذهاب إلى المصب، يساعد التيار
    السفينة؛ وبالتالي، فإن المعدل الفعلي للسفينة هو s + c.
    عند الصعود إلى المنبع، يؤدي التيار إلى إبطاء السفينة؛
    وبالتالي، فإن المعدل الفعلي هو s − c.    		 .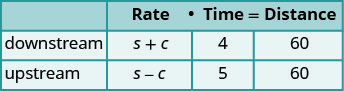
    يستغرق المصب 4 ساعات.
    يستغرق الأمر 5 ساعات عند المنبع.
    في كل اتجاه تكون المسافة 60 ميلاً.    		  
    ترجم إلى نظام من المعادلات.
    نظرًا لأن معدل الوقت هو المسافة، يمكننا
    كتابة نظام المعادلات.    		 .
    حل نظام المعادلات.
    قم بالتوزيع لوضع المعادلتين في
    الشكل القياسي، ثم قم بحلهما بالحذف.    		 .
    اضرب المعادلة العليا في 5 والمعادلة السفلية في 4.
    أضف المعادلات، ثم قم بحلها لـ s.    		 .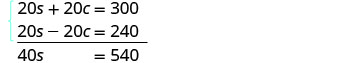
    استبدل s = 13.5 في إحدى المعادلات الأصلية. .
      .
      .
      .
     

    5.4-43. jpg
    تحقق من الإجابة في المشكلة.

    سيكون معدل المصب
    13.5 + 1.5 = 15 ميلاً في الساعة.
    في 4 ساعات ستسافر السفينة
    15 · 4 = 60 ميلاً.
    سيكون معدل المنبع
    13.5 - 1.5 = 12 ميلاً في الساعة.
    في غضون 5 ساعات ستسافر السفينة
    12 · 5 = 60 ميلاً.    		  
    أجب على السؤال. معدل السفينة هو 13.5 ميل في الساعة ومعدل التيار هو 1.5 ميل في الساعة.
    التمارين\(\PageIndex{26}\)

    ترجم إلى نظام من المعادلات ثم حُل: أبحرت رحلة بحرية في نهر المسيسيبي 120 ميلاً في اتجاه المنبع لمدة 12 ساعة ثم استغرقت 10 ساعات للعودة إلى الرصيف. ابحث عن سرعة القارب النهري في المياه الساكنة وسرعة تيار النهر.

    إجابة

    معدل القارب هو 11 ميل في الساعة ومعدل التيار هو 1 ميل في الساعة.

    التمارين\(\PageIndex{27}\)

    ترجم إلى نظام من المعادلات ثم قم بحلها: جدف جيسون قاربه على بعد 24 ميلاً من المنبع لمدة 4 ساعات. استغرق الأمر منه 3 ساعات للتجديف مرة أخرى. أوجد سرعة الزورق في الماء الساكن وسرعة تيار النهر.

    إجابة

    تبلغ سرعة الزورق 7 ميل في الساعة وسرعة التيار 1 ميل في الساعة.

    تؤثر تيارات الرياح على سرعات الطائرة بنفس الطريقة التي تؤثر بها التيارات المائية على سرعات القوارب. سنرى هذا في التمرين\(\PageIndex{28}\). يُطلق على تيار الرياح في نفس اتجاه تحليق الطائرة اسم الرياح الخلفية. يُطلق على تيار الرياح الذي يهب في اتجاه الطائرة اسم الرياح المعاكسة.

    التمارين\(\PageIndex{28}\)

    ترجم إلى نظام المعادلات ثم قم بحل:

    يمكن للطائرة الخاصة أن تطير 1095 ميلاً في ثلاث ساعات مع رياح خلفية ولكن فقط 987 ميلاً في ثلاث ساعات في رياح عكسية. أوجد سرعة الطائرة في الهواء الساكن وسرعة الرياح.

    إجابة

    اقرأ المشكلة.

    هذه مشكلة حركة موحدة وستساعدنا الصورة على التخيل.

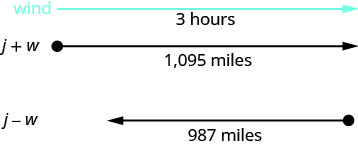
    يوضح هذا الشكل سهمًا يحمل عبارة «3 ساعات» ويستمر إلى اليمين ويمثل الريح. تحت الموجة يوجد شعاع يشير إلى اليمين ويطلق عليه «j plus w يساوي 365" و «1,095 ميلاً». تحت هذا الشعاع يوجد شعاع آخر يشير إلى اليسار المسمى «j ناقص w يساوي 329" و «987 ميلًا».

    حدد ما نبحث عنه. نحن نبحث عن سرعة الطائرة
    في الهواء الساكن وسرعة الرياح.
    اذكر ما نبحث عنه. دع j= سرعة الطائرة في الهواء الساكن.
    w = سرعة الرياح
    سيساعدنا المخطط على تنظيم المعلومات.
    تقوم الطائرة برحلتين - واحدة في الرياح الخلفية
    والأخرى في الرياح المعاكسة.
    في حالة الرياح الخلفية، تساعد الرياح الطائرة وبالتالي
    فإن المعدل هو j + w.
    في حالة الرياح المعاكسة، تؤدي الرياح إلى إبطاء التدفق
    وبالتالي يكون المعدل j − w.    		 .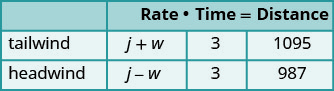
    تستغرق كل رحلة 3 ساعات.
    في الرياح الخلفية، تطير الطائرة لمسافة 1095 ميلاً.
    في الرياح المعاكسة تطير الطائرة 987 ميلاً.    		  
    ترجم إلى نظام من المعادلات.
    نظرًا لأن معدل الوقت هو المسافة، نحصل على
    نظام المعادلات.    		 .
    حل نظام المعادلات.
    قم بالتوزيع ثم الحل عن طريق الإزالة.    		 .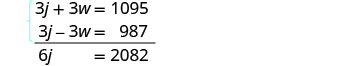
    إضافة وحل لـ j.

    استبدل j = 347 في إحدى
    المعادلات الأصلية، ثم قم بحل w.    		 .
      .
      .
      .
      .
    تحقق من الإجابة في المشكلة.

    مع الرياح الخلفية، سيكون المعدل الفعلي
    للطائرة
    347 + 18 = 365 ميلاً في الساعة.
    في غضون 3 ساعات ستسافر الطائرة
    365 · 3 = 1095 ميلاً.
    عند مواجهة الرياح المعاكسة، سيكون
    المعدل الفعلي للطائرة
    347 − 18 = 329 ميلاً في الساعة.
    في غضون 3 ساعات ستسافر الطائرة
    329 · 3 = 987 ميلاً.    		  
    أجب على السؤال. يبلغ معدل الطائرة 347 ميلاً في الساعة
    ومعدل الرياح 18 ميلاً في الساعة.
    التمارين\(\PageIndex{29}\)

    قم بالترجمة إلى نظام من المعادلات ثم قم بحل: يمكن لطائرة صغيرة أن تطير 1325 ميلاً في 5 ساعات مع الرياح الخلفية ولكن فقط 1025 ميلاً في 5 ساعات في رياح عكسية. أوجد سرعة الطائرة في الهواء الساكن وسرعة الرياح.

    إجابة

    تبلغ سرعة الطائرة 235 ميلاً في الساعة وسرعة الرياح 30 ميلاً في الساعة.

    التمارين\(\PageIndex{30}\)

    ترجم إلى نظام من المعادلات ثم قم بحل: يمكن لطائرة تجارية أن تطير 1728 ميلاً في 4 ساعات مع الرياح الخلفية ولكن فقط 1536 ميلاً في 4 ساعات في رياح عكسية. أوجد سرعة الطائرة في الهواء الساكن وسرعة الرياح.

    إجابة

    تبلغ سرعة الطائرة 408 ميلاً في الساعة وسرعة الرياح 24 ميلاً في الساعة.

    مسرد المصطلحات

    زوايا تكميلية
    تتكامل زاويتان إذا كان مجموع قياسات زواياهما\(90\) درجات.
    زوايا تكميلية
    تكون زاويتان متكاملتان إذا كان مجموع قياسات زواياهما\(180\) درجات.