5.3: حل أنظمة المعادلات بالحذف
- Page ID
- 200109
في نهاية هذا القسم، ستكون قادرًا على:
- حل نظام المعادلات بالحذف
- حل تطبيقات أنظمة المعادلات بالحذف
- اختر الطريقة الأكثر ملاءمة لحل نظام المعادلات الخطية
قبل البدء، قم بإجراء اختبار الجاهزية هذا.
- قم بتبسيط −5 (6-3a).
إذا فاتتك هذه المشكلة، راجع التمرين 1.10.43. - حل المعادلة\(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\).
إذا فاتتك هذه المشكلة، راجع التمرين 2.5.1.
لقد قمنا بحل أنظمة المعادلات الخطية عن طريق الرسوم البيانية والاستبدال. يعمل الرسم البياني جيدًا عندما تكون المعاملات المتغيرة صغيرة ويكون للحل قيم عددية. يعمل الاستبدال جيدًا عندما نتمكن بسهولة من حل معادلة واحدة لأحد المتغيرات وعدم وجود عدد كبير جدًا من الكسور في التعبير الناتج.
الطريقة الثالثة لحل أنظمة المعادلات الخطية تسمى طريقة الحذف. عندما حللنا نظامًا عن طريق الاستبدال، بدأنا بمعادلتين ومتغيرين وخفضناه إلى معادلة واحدة بمتغير واحد. هذا ما سنفعله مع طريقة الإزالة أيضًا، ولكن سيكون لدينا طريقة مختلفة للوصول إلى هناك.
حل نظام المعادلات بالحذف
تعتمد طريقة الحذف على خاصية إضافة المساواة. تقول خاصية الجمع للمساواة أنه عندما تضيف نفس الكمية إلى كلا طرفي المعادلة، تظل لديك المساواة. سنقوم بتوسيع خاصية إضافة المساواة لنقول أنه عند إضافة كميات متساوية لكلا طرفي المعادلة، تكون النتائج متساوية.
لأي تعبيرات أ، ب، ج، د،
\[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]
لحل نظام المعادلات بالحذف، نبدأ بكلتا المعادلتين في الشكل القياسي. ثم نقرر أي متغير سيكون من الأسهل إزالته. كيف نقرر؟ نريد أن تكون معاملات متغير واحد أضداد، حتى نتمكن من جمع المعادلات معًا وإزالة هذا المتغير.
لاحظ كيف يعمل ذلك عندما نجمع هاتين المعادلتين معًا:
\[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]
يتم إضافة y إلى الصفر ولدينا معادلة واحدة بمتغير واحد.
دعونا نجرب واحدة أخرى:
\[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]
هذه المرة لا نرى متغيرًا يمكن حذفه فورًا إذا أضفنا المعادلات.
ولكن إذا ضربنا المعادلة الأولى في −2، فسنصنع معاملات x الأضداد. يجب أن نضرب كل حد على جانبي المعادلة في −2.
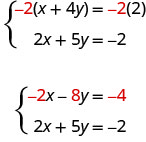
نرى الآن أن معاملات مصطلحات x هي أضداد، لذلك سيتم حذف x عندما نضيف هاتين المعادلتين.
أضف المعادلات بنفسك - يجب أن تكون النتيجة −3 y = −6. وهذا يبدو سهل الحل، أليس كذلك؟ هذا ما سيبدو عليه.
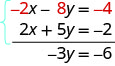
سنفعل واحدة أخرى:
\[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]
لا يبدو أننا نستطيع جعل معاملات متغير واحد أضداد بضرب إحدى المعادلات في ثابت، ما لم نستخدم الكسور. لذا بدلاً من ذلك، سيتعين علينا ضرب المعادلتين في ثابت.
يمكننا أن نجعل معاملات x أضداد إذا ضربنا المعادلة الأولى في 3 والثانية في −4، بحيث نحصل على 12 x و−12 x.
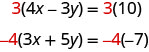
هذا يعطينا هاتين المعادلتين الجديدتين:
\[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]
عندما نضيف هذه المعادلات،
\[\[\left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]\]
يتم حذف x ولدينا فقط −29 y = 58.
بمجرد أن نحصل على معادلة بمتغير واحد فقط، نقوم بحلها. ثم نستبدل هذه القيمة بإحدى المعادلات الأصلية لحلها للمتغير المتبقي. وكما هو الحال دائمًا، نتحقق من إجابتنا للتأكد من أنها حل لكل من المعادلتين الأصليتين.
سنرى الآن كيفية استخدام الحذف لحل نفس نظام المعادلات الذي قمنا بحله عن طريق التمثيل البياني والاستبدال.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- إجابة
-







حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)
- إجابة
-
(2، −1)
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)
- إجابة
-
(−2,3)
يتم سرد الخطوات أدناه للرجوع إليها بسهولة.
- اكتب المعادلتين في الصورة القياسية. إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
- قم بعمل معاملات أضداد متغير واحد.
- حدد المتغير الذي ستقوم بإزالته.
- اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد.
- أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل الحل من الخطوة 4 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.
سنقوم أولاً بعمل مثال حيث يمكننا إزالة متغير واحد على الفور.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)
- إجابة
-

كلا المعادلتين في الشكل القياسي. معاملات y هي بالفعل أضداد. أضف المعادلتين لإزالة y.
تحتوي المعادلة الناتجة على متغير واحد فقط، x.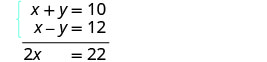
حل لـ x، المتغير المتبقي.
استبدل x = 11 في إحدى المعادلات الأصلية.

حل للمتغير الآخر، y. 
اكتب الحل كزوج مطلوب. الزوج الذي تم ترتيبه هو (11، −1). تأكد من أن الزوج المطلوب هو حل لكل
من المعادلتين الأصليتين.
\(\begin{array}{rllrll} x+y &=&10 &x-y&=&12\\ 11+(-1) &\stackrel{?}{=}&10 & 11-(-1) &\stackrel{?}{=}&12\\ 10 &=&10 \checkmark & 12 &=&12 \checkmark \end{array}\)الحل هو (11، −1).
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)
- إجابة
-
(3، −1)
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)
- إجابة
-
(−2,5)
في التمرين\(\PageIndex{7}\)، سنتمكن من إجراء معاملات أحد المتغيرات الأضداد بضرب معادلة واحدة في ثابت.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)
- إجابة
-

كلا المعادلتين في الشكل القياسي. لا يوجد أي من المعاملات متضادة. يمكننا تكوين معاملات أضداد y بضرب
المعادلة الأولى في −3.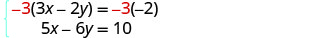
قم بالتبسيط. 
أضف المعادلتين لإزالة y. 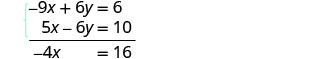
حل للمتغير المتبقي، x.
استبدل x = −4 بإحدى المعادلات الأصلية.

حل من أجلك. 


اكتب الحل كزوج مطلوب. الزوج المُرتَّب هو (−4، −5). تأكد من أن الزوج المطلوب هو حل
لكل من المعادلتين الأصليتين.
\(\begin{array}{rllrll} 3x-2y &=&-2 &5x-6y&=&10\\ 3(-4)-2(-5) &\stackrel{?}{=}&-2 & 5(-4)-6(-5) &\stackrel{?}{=}&10\\ -12+10&\stackrel{?}{=}&-2 &-20+30&\stackrel{?}{=}&10\\-2 &=&-2 \checkmark & 10 &=&10 \checkmark \end{array}\)الحل هو (−4، −5).
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)
- إجابة
-
(1,1)
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)
- إجابة
-
(−2,4)
الآن سنقوم بعمل مثال حيث نحتاج إلى ضرب كلتا المعادلتين بالثوابت من أجل جعل معاملات أضداد متغير واحد.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)
- إجابة
-
في هذا المثال، لا يمكننا ضرب معادلة واحدة فقط بأي ثابت للحصول على معاملات عكسية. لذلك سنضرب كلا المعادلتين بشكل استراتيجي بثابت للحصول على الأضداد.

كلا المعادلتين في الشكل القياسي. للحصول على
معاملات عكسية لـ y، سنضرب المعادلة الأولى في 2
والمعادلة الثانية في 3.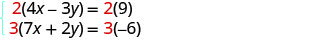
قم بالتبسيط. 
أضف المعادلتين لإزالة y. 
حل لـ x.
استبدل x = 0 في إحدى المعادلات الأصلية.

حل من أجلك. 

اكتب الحل كزوج مطلوب. الزوج المطلوب هو (0، −3). تأكد من أن الزوج المطلوب هو حل
لكل من المعادلتين الأصليتين.
\(\begin{array}{rllrll} 4x-3y &=&9 &7x+2y&=&-6\\ 4(0)-3(-3) &\stackrel{?}{=}&9 & 7(0)+2(-3) &\stackrel{?}{=}&-6\\9 &=&9 \checkmark & -6 &=&-6 \checkmark \end{array}\)الحل هو (0، −3).
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)
- إجابة
-
(1,3)
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)
- إجابة
-
(4، −3)
عندما يحتوي نظام المعادلات على كسور، سنقوم أولاً بمسح الكسور بضرب كل معادلة في شاشة LCD الخاصة بها.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)
- إجابة
-
في هذا المثال، تحتوي كلتا المعادلتين على كسور. ستكون خطوتنا الأولى هي ضرب كل معادلة في شاشة LCD الخاصة بها لمسح الكسور.
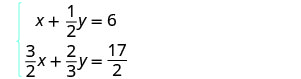
لمسح الكسور، اضرب كل معادلة في شاشة LCD الخاصة بها. 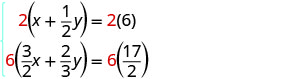
قم بالتبسيط. 
الآن نحن على استعداد للقضاء على أحد المتغيرات. لاحظ أن
كلا المعادلتين في الشكل القياسي.يمكننا القضاء عن طريق ضرب المعادلة العليا في −4. 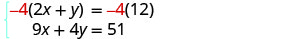
قم بالتبسيط والإضافة.
استبدل x = 3 في إحدى المعادلات الأصلية.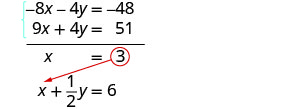
حل من أجلك. 


اكتب الحل كزوج مطلوب. الزوج المطلوب هو (3، 6). تأكد من أن الزوج المطلوب هو حل لكل
من المعادلتين الأصليتين.
\(\begin{array}{rllrll} x+\frac{1}{2}y &=&6 &\frac{3}{2}x+\frac{2}{3}y&=&\frac{17}{2}\\ 3+\frac{1}{2}(6) &\stackrel{?}{=}&6 &\frac{3}{2}(3) + \frac{2}{3}(6)&\stackrel{?}{=}&\frac{17}{2}\\ 3 + 3 &\stackrel{?}{=}&6 & \frac{9}{2 }+4 &\stackrel{?}{=} & \frac{17}{2}\\ 6 &=&6 \checkmark & \frac{9}{2} + \frac{8}{2} &\stackrel{?}{=} & \frac{17}{2}\\ && & \frac{17}{2} &=&\frac{17}{2} \checkmark \end{array}\)الحل هو (3، 6).
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)
- إجابة
-
(6,2)
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)
- إجابة
-
(1، −2)
في حل أنظمة المعادلات بالرسم البياني، رأينا أنه لا تحتوي جميع أنظمة المعادلات الخطية على زوج واحد مرتب كحل. عندما كانت المعادلتين في الواقع نفس الخط، كان هناك عدد لا نهائي من الحلول. أطلقنا على ذلك نظامًا ثابتًا. عندما وصفت المعادلتين الخطوط المتوازية، لم يكن هناك حل. أطلقنا على ذلك نظامًا غير متناسق.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)
- إجابة
-
\(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)
هذا بيان حقيقي. المعادلات متسقة ولكنها تعتمد. ستكون الرسوم البيانية الخاصة بهم هي نفس السطر. يحتوي النظام على العديد من الحلول بلا حدود.
بعد مسح الكسور في المعادلة الثانية، هل لاحظت أن المعادلتين متماثلتان؟ هذا يعني أن لدينا خطوطًا متزامنة.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)
- إجابة
-
العديد من الحلول بلا حدود
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)
- إجابة
-
العديد من الحلول بلا حدود
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)
- إجابة
-
\(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)
هذه العبارة خاطئة. المعادلات غير متناسقة وبالتالي ستكون رسوماتها البيانية عبارة عن خطوط متوازية.
لا يحتوي النظام على حل.
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل النظام عن طريق الإزالة. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)
- إجابة
-
لا يوجد حل
حل تطبيقات أنظمة المعادلات بالحذف
تُترجم بعض مشكلات التطبيقات مباشرة إلى معادلات في النموذج القياسي، لذلك سنستخدم طريقة الحذف لحلها. كما هو الحال من قبل، نستخدم إستراتيجية حل المشكلات الخاصة بنا لمساعدتنا على الاستمرار في التركيز والتنظيم.
مجموع الرقمين هو 39. الفرق بينهما هو 9. ابحث عن الأرقام.
- إجابة
-
\(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)
مجموع الرقمين هو 42. الفرق بينهما هو 8. ابحث عن الأرقام.
- إجابة
-
الأرقام هي 25 و 17.
مجموع عددين هو −15. الفرق بينهما هو −35. ابحث عن الأرقام.
- إجابة
-
الأرقام هي −25 و10.
يتوقف جو في مطعم برغر كل يوم في طريقه إلى العمل. يوم الاثنين كان لديه طلب واحد من البطاطس المقلية المتوسطة واثنين من المشروبات الغازية الصغيرة، والتي تحتوي على ما مجموعه 620 سعرة حرارية. حصل يوم الثلاثاء على طلبين من البطاطس المقلية المتوسطة والصودا الصغيرة بإجمالي 820 سعرة حرارية. كم عدد السعرات الحرارية الموجودة في الترتيب الواحد من البطاطس المقلية المتوسطة؟ كم عدد السعرات الحرارية في صودا صغيرة واحدة؟
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. نحن نبحث عن عدد
السعرات الحرارية بترتيب واحد من البطاطس المقلية المتوسطة
وفي صودا صغيرة واحدة.الخطوة 3. اذكر ما نبحث عنه. Let f = عدد السعرات الحرارية في ترتيب
واحد من البطاطس المقلية المتوسطة.
s = عدد السعرات الحرارية في
1 صودا صغيرة.الخطوة 4. ترجم إلى نظام المعادلات: تحتوي حبة بطاطس متوسطة الحجم واثنين من المشروبات الغازية الصغيرة على
إجمالي 620 سعرًا حراريًا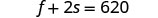
تحتوي بطاطس مقلية متوسطة الحجم وواحدة صغيرة من الصودا على
إجمالي 820 سعرة حرارية.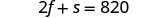
نظامنا هو: 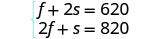
الخطوة 5. حل نظام المعادلات.
لحل نظام المعادلات، استخدم
الحذف. المعادلات في
الشكل القياسي. للحصول على معاملات عكسية لـ f،
اضرب المعادلة العليا في −2.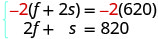
قم بالتبسيط والإضافة. 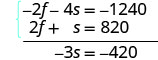
حل لنا. 
استبدل s = 140 في إحدى
المعادلات الأصلية ثم قم بحل f.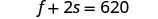
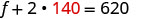
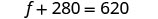
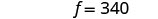
الخطوة 6. تحقق من الإجابة. تحقق من أن هذه الأرقام منطقية
في المشكلة وأنها
حلول لكلتا المعادلتين.
نترك هذا لك!الخطوة 7. أجب على السؤال. تحتوي الصودا الصغيرة على 140 سعرة حرارية والبطاطا المقلية
على 340 سعرة حرارية.
يتوقف مالك عند متجر البقالة لشراء كيس من الحفاضات وعلبتين من الحليب الصناعي. ينفق ما مجموعه 37 دولارًا. في الأسبوع التالي، توقف واشترى حقيبتين من الحفاضات و 5 علب من الحليب الصناعي بإجمالي 87 دولارًا. كم تبلغ تكلفة حقيبة الحفاضات؟ كم سعر علبة واحدة من الصيغة؟
- إجابة
-
تبلغ تكلفة حقيبة الحفاضات 11 دولارًا وعلبة الصيغة 13 دولارًا.
للحصول على تناولها اليومي من الفاكهة لهذا اليوم، تأكل ساشا موزة و 8 حبات فراولة يوم الأربعاء مقابل 145 سعرًا حراريًا. في يوم الأربعاء التالي، تناولت اثنين من الموز و 5 حبات من الفراولة ليصبح المجموع 235 سعرًا حراريًا للفاكهة. كم عدد السعرات الحرارية الموجودة في الموز؟ كم عدد السعرات الحرارية في الفراولة؟
- إجابة
-
هناك 105 سعرة حرارية في الموز و 5 سعرات حرارية في الفراولة.
اختر الطريقة الأكثر ملاءمة لحل نظام المعادلات الخطية
عندما يتعين عليك حل نظام المعادلات الخطية في فصل الرياضيات اللاحق، لن يتم إخبارك عادةً بالطريقة التي يجب استخدامها. سوف تحتاج إلى اتخاذ هذا القرار بنفسك. لذلك ستحتاج إلى اختيار الطريقة الأسهل للقيام بها وتقليل فرصتك في ارتكاب الأخطاء.

بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
- \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
- \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
- إجابة
-
1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
نظرًا لأن كلتا المعادلتين في الشكل القياسي، فإن استخدام الحذف سيكون أكثر ملاءمة.
2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ y، فإن استخدام الاستبدال سيكون أكثر ملاءمة.
بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
- \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)
- إجابة
-
- نظرًا لأن كلتا المعادلتين في الشكل القياسي، فإن استخدام الحذف سيكون أكثر ملاءمة.
- نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ xx، فإن استخدام الاستبدال سيكون أكثر ملاءمة.
بالنسبة لكل نظام من المعادلات الخطية، حدد ما إذا كان من الأنسب حلها عن طريق الاستبدال أو الحذف. اشرح إجابتك.
- \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
- \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)
- إجابة
-
- نظرًا لأن معادلة واحدة قد تم حلها بالفعل لـ yy، فإن استخدام الاستبدال سيكون أكثر ملاءمة؛
- نظرًا لأن كلتا المعادلتين في الشكل القياسي، فإن استخدام الحذف سيكون أكثر ملاءمة.
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل أنظمة المعادلات الخطية عن طريق الحذف.
- فيديو تعليمي - حل أنظمة المعادلات بالحذف
- حل الفيديو التعليمي عن طريق الاستبعاد
- أنظمة حل الفيديو التعليمية عن طريق الاستبعاد
المفاهيم الرئيسية
- حل نظام المعادلات بالحذف
- اكتب المعادلتين في الصورة القياسية. إذا كانت أي معاملات عبارة عن كسور، فقم بإزالتها.
- قم بعمل معاملات أضداد متغير واحد.
- حدد المتغير الذي ستقوم بإزالته.
- اضرب معادلتين أو كلتيهما بحيث تكون معاملات هذا المتغير أضداد.
- أضف المعادلات الناتجة من الخطوة 2 لإزالة متغير واحد.
- حل للمتغير المتبقي.
- استبدل الحل من الخطوة 4 بإحدى المعادلات الأصلية. ثم قم بحل المتغير الآخر.
- اكتب الحل كزوج مطلوب.
- تأكد من أن الزوج المطلوب هو حل لكل من المعادلتين الأصليتين.


