3.4: المثلثات والمستطيلات ونظرية فيثاغورس

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• حل التطبيقات باستخدام خصائص المثلثات
• استخدم نظرية فيثاغورس
• حل التطبيقات باستخدام خصائص المستطيل

كن مستعدًا

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بالتبسيط:\(12(6h)\).
   إذا فاتتك هذه المشكلة، راجع التمرين 1.10.1.
2. يقل طول المستطيل عن العرض بثلاثة أضعاف. دعونا نمثل العرض. اكتب مقدارًا يُعبِّر عن طول المستطيل.
   إذا فاتتك هذه المشكلة، راجع التمرين 1.3.43.
3. الحل:\(A=\frac{1}{2}bh\) لـ b عندما A = 260 و h = 52.
   إذا فاتتك هذه المشكلة، راجع التمرين 2.6.10.
4. قم بالتبسيط:\(\sqrt{144}\).
   إذا فاتتك هذه المشكلة، راجع التمرين 1.9.10.

حل التطبيقات باستخدام خصائص المثلثات

في هذا القسم سوف نستخدم بعض الصيغ الهندسية الشائعة. سنقوم بتكييف إستراتيجيتنا لحل المشكلات حتى نتمكن من حل التطبيقات الهندسية. ستقوم الصيغة الهندسية بتسمية المتغيرات وتعطينا المعادلة التي يجب حلها. بالإضافة إلى ذلك، نظرًا لأن جميع هذه التطبيقات ستشمل أشكالًا من نوع ما، يجد معظم الأشخاص أنه من المفيد رسم الشكل وتسميته بالمعلومات المحددة. سنقوم بتضمين هذا في الخطوة الأولى من استراتيجية حل المشكلات لتطبيقات الهندسة.

حل تطبيقات الهندسة

1. اقرأ المشكلة وتأكد من فهم جميع الكلمات والأفكار. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
2. حدد ما نبحث عنه.
3. قم بتسمية ما نبحث عنه عن طريق اختيار متغير لتمثيله.
4. ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
6. تحقق من الإجابة عن طريق استبدالها مرة أخرى في المعادلة التي تم حلها في الخطوة 5 والتأكد من أنها منطقية في سياق المشكلة.
7. أجب على السؤال بجملة كاملة.

سنبدأ تطبيقات الهندسة من خلال النظر في خصائص المثلثات. دعونا نراجع بعض الحقائق الأساسية حول المثلثات. المثلثات لها ثلاثة أضلاع وثلاث زوايا داخلية. عادةً ما يتم تسمية كل جانب بحرف صغير ليطابق الحرف الكبير من الرأس المقابل.

صيغة الجمع لكلمة قمة الرأس هي الرؤوس. تحتوي جميع المثلثات على ثلاثة رؤوس. تتم تسمية المثلثات برءوسها:\(\PageIndex{1}\) يسمى المثلث في الشكل\(\triangle{ABC}\).

الشكل\(\PageIndex{1}\): مثلث ABC له رءوس\(A\)\(B\) و و\(C\). أطوال الجوانب هي\(a\)، و\(b\)، و\(c\).

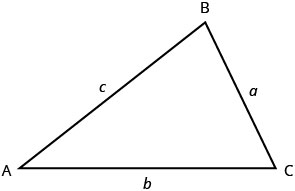
ترتبط الزوايا الثلاث للمثلث بطريقة خاصة. مجموع مقاييسهم هو\(180^{\circ}\). لاحظ أننا نقرأ\(m\angle{A}\) كـ «مقياس الزاوية A». لذلك\(\triangle{ABC}\) في الشكل\(\PageIndex{1}\).

\[m \angle A+m \angle B+m \angle C=180^{\circ} \nonumber\]

نظرًا لأن محيط الشكل هو طول حدوده، فإن محيطه\(\triangle{ABC}\) هو مجموع أطوال أضلاعه الثلاثة.

\[P = a + b + c \nonumber\]

لإيجاد مساحة المثلث، نحتاج إلى معرفة قاعدته وارتفاعه. الارتفاع هو خط يربط القاعدة بالرأس المعاكس ويصنع\(90^\circ\) زاوية مع القاعدة. سنرسم\(\triangle{ABC}\) مرة أخرى، ونعرض الآن الارتفاع،\(h\). انظر الشكل\(\PageIndex{2}\).

الشكل\(\PageIndex{2}\): صيغة المنطقة\(\triangle{ABC}\) هي\(A = \frac{1}{2}bh\) حيث b هي القاعدة و h هي الارتفاع.

خصائص المثلث

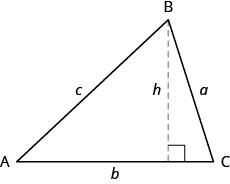
بالنسبة\(\triangle{ABC}\)

قياسات الزاوية:

\[m \angle A+m \angle B+m \angle C=180^{\circ}\]

• مجموع قياسات زوايا المثلث هو 180°.

محيط:

\[P = a + b + c\]

• المحيط هو مجموع أطوال أضلاع المثلث.

المنطقة:

\(A = \frac{1}{2}bh, b = \text{ base }, h = \text{ height }\)

• مساحة المثلث تساوي نصف القاعدة في الارتفاع.

مثال\(\PageIndex{1}\)

قياسات زاويتي المثلث هما 55 و82 درجة. أوجد قياس الزاوية الثالثة.

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.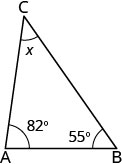
الخطوة 2. حدد ما تبحث عنه.	قياس الزاوية الثالثة في المثلث
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	\(x=\)دع قياس الزاوية.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة واستبدلها.	\(m \angle A+m \angle B+m \angle C=180^{\circ}\)
الخطوة 5. حل المعادلة.	\(\begin{array} {rll} {55 + 82 + x} &{=} &{180} \\ {137 + x} &{=} &{180} \\ {x} &{=} &{43} \end{array}\)
الخطوة 6. تحقق. \(\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	قياس الزاوية الثالثة هو 43 درجة.

جرب ذلك\(\PageIndex{1}\)

قياسات زاويتي المثلث هي 31 و 128 درجة. أوجد قياس الزاوية الثالثة.

إجابة

21 درجة

جرب ذلك\(\PageIndex{2}\)

قياسات زاويتي المثلث هما 49 و75 درجة. أوجد قياس الزاوية الثالثة.

إجابة

56 درجة

مثال\(\PageIndex{2}\)

يبلغ محيط الحديقة المثلثة 24 قدمًا. يبلغ طول الجانبين أربعة أقدام وتسعة أقدام. ما هي مدة الجانب الثالث؟

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.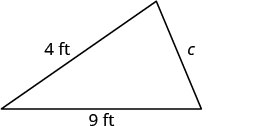
الخطوة 2. حدد ما تبحث عنه.	طول الجانب الثالث من المثلث
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	دع\(c=\) الجانب الثالث.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة واستبدلها.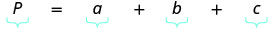
استبدل المعلومات المعطاة.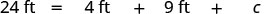
الخطوة 5. حل المعادلة.
الخطوة 6. تحقق. \(\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11} \\ {24} &{=} &{24\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	يبلغ طول الجانب الثالث 11 قدمًا.

جرب ذلك\(\PageIndex{3}\)

يبلغ محيط الحديقة المثلثة 48 قدمًا. يبلغ طول الجانبين 18 قدمًا و22 قدمًا. ما هي مدة الجانب الثالث؟

إجابة

8 أقدام

جرب ذلك\(\PageIndex{4}\)

يبلغ طول جانبي النافذة المثلثة سبعة أقدام وخمسة أقدام. محيط المكان 18 قدمًا. ما هي مدة الجانب الثالث؟

إجابة

6 أقدام

مثال\(\PageIndex{3}\)

تبلغ مساحة نافذة الكنيسة الثلاثية 90 مترًا مربعًا. تبلغ قاعدة النافذة 15 مترًا. ما هو ارتفاع النافذة؟

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.	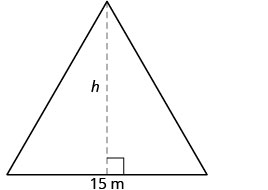\(\text{ Area } = 90m^{2}\)
الخطوة 2. حدد ما تبحث عنه.	ارتفاع المثلث
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	\(h=\)دع الارتفاع.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.
استبدل المعلومات المعطاة.
الخطوة 5. حل المعادلة.	\(90 = \dfrac{15}{2}h\) \(12 = h\)
الخطوة 6. تحقق. \(\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	يبلغ ارتفاع المثلث 12 مترًا.

جرب ذلك\(\PageIndex{5}\)

تبلغ مساحة اللوحة الثلاثية 126 بوصة مربعة. القاعدة هي 18 بوصة. ما هو الارتفاع؟

إجابة

14 بوصة

جرب ذلك\(\PageIndex{6}\)

تبلغ مساحة باب الخيمة الثلاثي 15 قدمًا مربعًا. الارتفاع هو خمسة أقدام. ما هي القاعدة؟

إجابة

6 أقدام

تنطبق خصائص المثلث التي استخدمناها حتى الآن على جميع المثلثات. الآن سننظر إلى نوع معين من المثلث - المثلث الأيمن. المثلث الأيمن له زاوية واحدة بزاوية 90 درجة، والتي عادة ما نحددها بمربع صغير في الزاوية.

الشكل\(\PageIndex{3}\)

تعريف: المثلث الأيمن

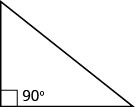
المثلث الأيمن له زاوية واحدة بزاوية 90 درجة، والتي غالبًا ما يتم تمييزها بمربع عند قمة الرأس.

مثال\(\PageIndex{4}\)

زاوية واحدة من المثلث القائم تساوي 28 درجة. ما قياس الزاوية الثالثة؟

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.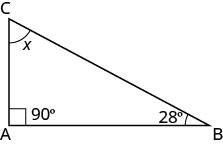
الخطوة 2. حدد ما تبحث عنه.	قياس الزاوية
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	\(x=\)دع قياس الزاوية.
الخطوة 4. ترجم.	\(m\angle{A} + m\angle{B} + m\angle{C} = 180\)
اكتب الصيغة المناسبة واستبدلها.	\(x+90+28=180\)
الخطوة 5. حل المعادلة.	\(x=62\)
الخطوة 6. تحقق. \(\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	قياس الزاوية الثالثة هو 62 ^درجة.

جرب ذلك\(\PageIndex{7}\)

زاوية واحدة من المثلث القائم تساوي 56 درجة. ما قياس الزاوية الصغيرة الأخرى؟

إجابة

34°

جرب ذلك\(\PageIndex{8}\)

زاوية واحدة من المثلث القائم تساوي 45 درجة. ما قياس الزاوية الصغيرة الأخرى؟

إجابة

45°

في الأمثلة التي رأيناها حتى الآن، يمكننا رسم شخصية وتسميتها مباشرة بعد قراءة المشكلة. في المثال التالي، سيتعين علينا تحديد زاوية واحدة بدلالة أخرى. سننتظر رسم الشكل حتى نكتب تعبيرات لجميع الزوايا التي نبحث عنها.

مثال\(\PageIndex{5}\)

يزيد قياس إحدى زوايا المثلث القائم على الزاوية بمقدار 20 درجة عن قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.

الحل

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	مقاييس الزوايا الثلاث
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	دع\(a=1^{st}\) الزاوية. \(a+20=2^{nd}\) \(90=3^{rd}\)زاوية الزاوية (الزاوية اليمنى)
ارسم الشكل وقم بتسميته بالمعلومات المعطاة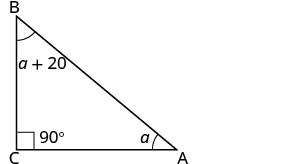
الخطوة 4. ترجم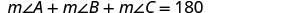
اكتب الصيغة المناسبة. استبدل الصيغة.	\(a + (a + 20) + 90 = 180\)
الخطوة 5. حل المعادلة.	\ (\ ابدأ {محاذاة *} 2a + 110 &= 180\\ [3pt] 2a &= 70\\ [3pt] a &= 35\ النص {الزاوية الأولى}\\\ [3pt] a &+ 20\ النص {الزاوية الثانية}\\ [3pt] {\ اللون {أحمر} {35}} و+ 20 = 55\ النهاية {محاذاة}}\) والزاوية الثالثة هي 90.
الخطوة 6. تحقق. \(\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	تقيس الزوايا الثلاث 35 ^درجة و 55 ^درجة و 90 ^درجة.

جرب ذلك\(\PageIndex{9}\)

يزيد قياس إحدى زوايا المثلث القائم على الزاوية بمقدار 50 درجة عن قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.

إجابة

20 درجة، 70 درجة، 90 درجة

جرب ذلك\(\PageIndex{10}\)

قياس إحدى زوايا المثلث القائم يزيد بمقدار 30 درجة عن قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.

إجابة

30 درجة، 60 درجة، 90 درجة

استخدم نظرية فيثاغورس

لقد تعلمنا كيف ترتبط قياسات زوايا المثلث ببعضها البعض. الآن، سوف نتعلم كيف ترتبط أطوال الجوانب ببعضها البعض. تُسمى نظرية فيثاغورس خاصية مهمة تصف العلاقة بين أطوال الأضلاع الثلاثة للمثلث القائم. تم استخدام هذه النظرية في جميع أنحاء العالم منذ العصور القديمة. سميت على اسم الفيلسوف اليوناني وعالم الرياضيات، فيثاغورس، الذي عاش حوالي 500 قبل الميلاد.

قبل أن نذكر نظرية فيثاغورس، نحتاج إلى إدخال بعض المصطلحات لأضلاع المثلث. تذكر أن المثلث الأيمن له زاوية 90 درجة، ومميز بمربع صغير في الزاوية. يُطلق على جانب المثلث المقابل للزاوية 90°90° اسم الوتر ويُسمى كل جانب من الجوانب الأخرى بالأرجل.

الشكل\(\PageIndex{4}\)

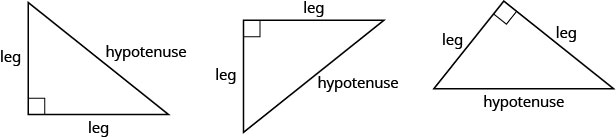
توضح نظرية فيثاغورس كيفية ارتباط أطوال الأضلاع الثلاثة للمثلث القائم الزاوية ببعضها البعض. وهي تنص على أنه في أي مثلث قائم الزاوية، يساوي مجموع مربعات أطوال الساقين مربع طول الوتر. في الرموز نقول: في أي مثلث قائم الزاوية\(a^{2}+b^{2}=c^{2}\)، حيث a و b هي أطوال الأرجل و cc هو طول الوتر.

قد تساعدك كتابة الصيغة في كل تمرين وقولها بصوت عالٍ أثناء كتابتها على تذكر نظرية فيثاغورس.

نظرية فيثاغورس

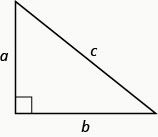
في أي مثلث قائم الزاوية، حيث\(a\)\(b\) توجد أطوال الأرجل،\(c\) يوجد طول الوتر.

ثم

\[a^{2}+b^{2}=c^{2} \label{Ptheorem}\]

لحل التمارين التي تستخدم نظرية فيثاغورس (المعادلة\ المرجع {نظرية})، سنحتاج إلى إيجاد الجذور التربيعية. لقد استخدمنا الترميز\(\sqrt{m}\) والتعريف:

إذا\(m = n^{2}\)، إذن\(\sqrt{m} = n\)، من أجل\(n\geq 0\).

على سبيل المثال، وجدنا أن هذا\(\sqrt{25}\) هو 5 بسبب\(25=5^{2}\).

نظرًا لأن نظرية فيثاغورس تحتوي على متغيرات مربعة، لحل مشكلة طول ضلع في مثلث قائم الزاوية، سيتعين علينا استخدام الجذور التربيعية.

مثال\(\PageIndex{6}\)

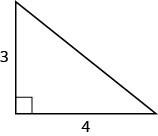
استخدم نظرية فيثاغورس لإيجاد طول الوتر الموضح أدناه.

الحل

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	طول وتر المثلث
الخطوة 3. اسم. اختر متغيرًا لتمثيله. ضع علامة على الجانب c على الشكل.	دع c = طول الوتر.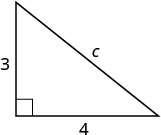
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.	\(a^{2} + b^{2} = c^{2}\)
بديل.	\(3^{2}+4^{2}=c^{2}\)
الخطوة 5. حل المعادلة.	\(9+16=c^{2}\)
قم بالتبسيط.	\(25=c^{2}\)
استخدم تعريف الجذر التربيعي.	\(\sqrt{25} = c\)
قم بالتبسيط.	\(5=c\)
الخطوة 6. تحقق.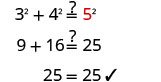
الخطوة 7. أجب على السؤال.	طول الوتر هو 5.

جرب ذلك\(\PageIndex{11}\)

استخدم نظرية فيثاغورس لإيجاد طول الوتر في المثلث الموضح أدناه.

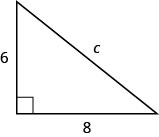
إجابة

ج = 10

جرب ذلك\(\PageIndex{12}\)

استخدم نظرية فيثاغورس لإيجاد طول الوتر في المثلث الموضح أدناه.

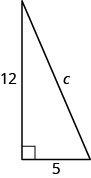
إجابة

ج = 13

مثال\(\PageIndex{7}\)

استخدم نظرية فيثاغورس لإيجاد طول الساق الموضح أدناه.

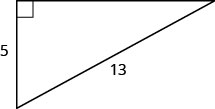
الحل

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	طول ساق المثلث
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	\(b=\)دع ساق المثلث.
جانب الملصق\(b\).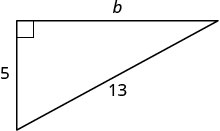
الخطوة 4. ترجم
اكتب الصيغة المناسبة.	\(a^{2} + b^{2} = c^{2}\)
بديل.	\(5^{2}+b^{2}=13^{2}\)
الخطوة 5. حل المعادلة.	\(25+b^{2}=169\)
اعزل مصطلح المتغير.	\(b^{2}=144\)
استخدم تعريف الجذر التربيعي.	\(b = \sqrt{144}\)
قم بالتبسيط.	\(b=12\)
الخطوة 6. تحقق.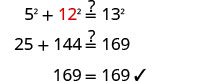
الخطوة 7. أجب على السؤال.	طول الساق هو 12.

جرب ذلك\(\PageIndex{13}\)

استخدم نظرية فيثاغورس لإيجاد طول الساق في المثلث الموضح أدناه.

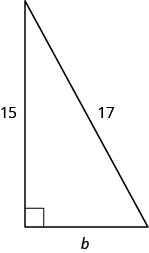
إجابة

8

جرب ذلك\(\PageIndex{14}\)

استخدم نظرية فيثاغورس لإيجاد طول الساق في المثلث الموضح أدناه.

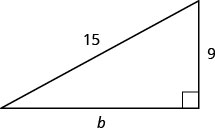
إجابة

12

مثال\(\PageIndex{8}\)

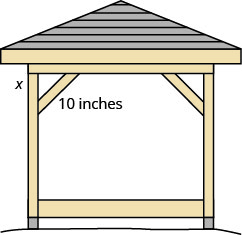
تقوم Kelvin ببناء شرفة وتريد دعم كل زاوية بوضع قطعة من الخشب بحجم 10 بوصات قطريًا كما هو موضح أعلاه.

إذا قام بربط الخشب بحيث تكون أطراف الدعامة على مسافة متساوية من الزاوية، فما طول أرجل المثلث القائم؟ تقريبًا لأقرب جزء من عُشر بوصة.

الحل

\(\begin{array} {ll} {\textbf{Step 1. }\text{Read the problem.}} &{} \\\\ {\textbf{Step 2. }\text{Identify what we are looking for.}} &{\text{the distance from the corner that the}} \\ {} &{\text{bracket should be attached}} \\ \\{\textbf{Step 3. }\text{Name. Choose a variable to represent it.}} &{\text{Let x = distance from the corner.}} \\ {\textbf{Step 4.} \text{Translate}} &{} \\ {\text{Write the appropriate formula and substitute.}} &{a^{2} + b^{2} = c^{2}} \\ {} &{x^{2} + x^{2} = 10^{2}} \\ \\ {\textbf{Step 5. Solve the equation.}} &{} \\ {} &{2x^{2} = 100} \\ {\text{Isolate the variable.}} &{x^{2} = 50} \\ {\text{Simplify. Approximate to the nearest tenth.}} &{x \approx 7.1}\\\\ {\textbf{Step 6. }\text{Check.}} &{}\\ {a^{2} + b^{2} = c^{2}} &{} \\ {(7.1)^{2} + (7.1)^{2} \approx 10^{2} \text{ Yes.}} &{} \\\\ {\textbf{Step 7. Answer the question.}} &{\text{Kelven should fasten each piece of}} \\ {} &{\text{wood approximately 7.1'' from the corner.}} \end{array}\)

جرب ذلك\(\PageIndex{15}\)

يضع جون قاعدة سلم طوله 13 قدمًا على بعد خمسة أقدام من جدار منزله كما هو موضح أدناه. إلى أي مدى يصل السلم إلى أعلى الجدار؟

إجابة

12 قدمًا

جرب ذلك\(\PageIndex{16}\)

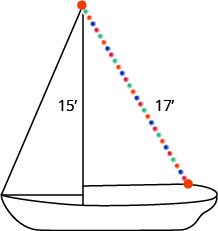
يريد راندي ربط سلسلة من الأضواء بطول 17 قدمًا في الجزء العلوي من سارية مركبه الشراعي التي يبلغ طولها 15 قدمًا، كما هو موضح أدناه. إلى أي مدى يجب أن يربط نهاية خيط الضوء من قاعدة الصاري؟

إجابة

8 أقدام

حل التطبيقات باستخدام خصائص المستطيل

قد تكون بالفعل على دراية بخصائص المستطيلات. تحتوي المستطيلات على أربعة جوانب وأربع زوايا قائمة (90 درجة). أضلاع المستطيل المقابلة لهما نفس الطول. نشير إلى أحد جانبي المستطيل بالطول\(L\)، والجانب المجاور له هو العرض،\(W\).

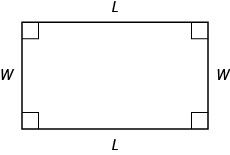
المسافة حول هذا المستطيل هي\(L+W+L+W\)، أو\(2L+2W\). هذا هو محيط المستطيل.\(P\)

\[P=2L+2W\]

ماذا عن مساحة المستطيل؟ تخيل سجادة مستطيلة طولها 2 قدم وعرضها 3 أقدام. تبلغ مساحتها 6 أقدام مربعة. هناك ستة مربعات في الشكل.

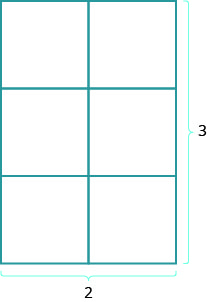
\[\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}\]

المنطقة هي الطول مضروبًا في العرض. صيغة مساحة المستطيل هي

\[A=LW.\]

خصائص المستطيلات

تحتوي المستطيلات على أربعة جوانب وأربع زوايا قائمة (90 درجة).

أطوال الأضلاع المقابلة متساوية.

محيط المستطيل هو مجموع ضعف الطول وضعف العرض.

\[P=2L+2W\]

مساحة المستطيل هي نتاج الطول والعرض.

\[A=L·W\]

مثال\(\PageIndex{9}\)

طول المستطيل 32 مترًا وعرضه 20 مترًا. ما هو المحيط؟

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
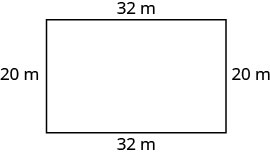الخطوة 2. حدد ما تبحث عنه.	محيط المستطيل
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	دع\(P=\) المحيط.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.
بديل.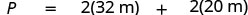
الخطوة 5. حل المعادلة.	\(P = 64 + 40\) \(P = 104\)
الخطوة 6. تحقق. \(\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{=}} &{104} \\ {104} &{=} &{104\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	محيط المستطيل يساوي ١٠٤ أمتار.

جرب ذلك\(\PageIndex{17}\)

طول المستطيل 120 ياردة وعرضه 50 ياردة. ما هو المحيط؟

إجابة

340 ياردة

جرب ذلك\(\PageIndex{18}\)

طول المستطيل 62 قدمًا وعرضه 48 قدمًا. ما هو المحيط؟

إجابة

220 قدمًا

مثال\(\PageIndex{10}\)

تبلغ مساحة الغرفة المستطيلة 168 قدمًا مربعًا. الطول هو 14 قدمًا. ما هو العرض؟

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
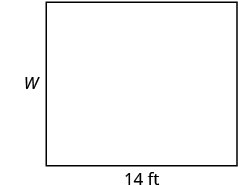الخطوة 2. حدد ما تبحث عنه.	عرض غرفة مستطيلة
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	دع\(W=\) العرض.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.	\(A=LW\)
بديل.	\(168 = 14W\)
الخطوة 5. حل المعادلة.	\(\frac{168}{14} = \frac{14W}{14}\) \(12 = W\)
الخطوة 6. تحقق. \(\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ {168} &{=} &{168\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	يبلغ عرض الغرفة 12 قدمًا.

جرب ذلك\(\PageIndex{19}\)

تبلغ مساحة المستطيل 598 قدمًا مربعًا. الطول هو 23 قدمًا. ما هو العرض؟

إجابة

26 قدمًا

جرب ذلك\(\PageIndex{20}\)

عرض المستطيل يساوي 21 مترًا. تبلغ مساحة المنطقة 609 متر مربع. ما هو الطول؟

إجابة

29 مترًا

مثال\(\PageIndex{11}\)

أوجد طول مستطيل محيطه ٥٠ بوصة وعرضه ١٠ بوصات.

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
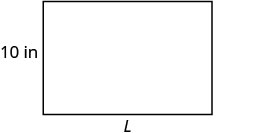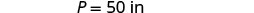الخطوة 2. حدد ما تبحث عنه.	طول المستطيل
الخطوة 3. اسم. اختر متغيرًا لتمثيله.	\(L=\)دع الطول.
الخطوة 4. ترجم.
اكتب الصيغة المناسبة.	\(P = 2L + 2W\)
بديل.	\(50 = 2L + 2(10)\)
الخطوة 5. حل المعادلة.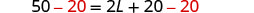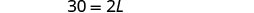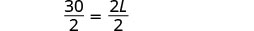
الخطوة 6. تحقق. \(\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	الطول هو 15 بوصة.

جرب ذلك\(\PageIndex{21}\)

أوجد طول المستطيل: محيطه ٨٠ وعرضه ٢٥.

إجابة

15

جرب ذلك\(\PageIndex{22}\)

أوجد طول المستطيل: محيطه ٣٠ وعرضه ٦.

إجابة

9

لقد قمنا بحل المشكلات حيث تم تحديد الطول أو العرض، جنبًا إلى جنب مع المحيط أو المنطقة؛ الآن سنتعلم كيفية حل المشكلات التي يتم فيها تحديد العرض من حيث الطول. سننتظر رسم الشكل حتى نكتب تعبيرًا للعرض حتى نتمكن من تسمية جانب واحد بهذا التعبير.

مثال\(\PageIndex{12}\)

يقل عرض المستطيل بمقدار قدمين عن الطول. محيط المبنى هو 52 قدمًا. ابحث عن الطول والعرض.

الحل

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	طول وعرض المستطيل
الخطوة 3. اسم. اختر متغيرًا لتمثيله. نظرًا لأن العرض محدد من حيث الطول، فإننا نسمح\(L=\) بالطول. العرض أقل بمقدار قدمين من الطول، لذلك نسمح\(L-2\) بالعرض.	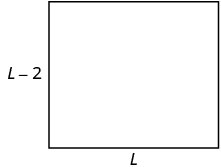\(P=52\)قدم
الخطوة 4. ترجم.
اكتب الصيغة المناسبة. تربط صيغة محيط المستطيل جميع المعلومات.	\(P=2L+2W\)
استبدل المعلومات المعطاة.	\(52=2L+2(L−2)\)
الخطوة 5. حل المعادلة.	\(52=2L+2L−4\)
اجمع بين المصطلحات المتشابهة.	\(52=4L−4\)
أضف 4 إلى كل جانب.	\(56 = 4L\)
قسّم على 4.	\(\frac{56}{4} = \frac{4L}{4}\) \(14=L\) الطول هو 14 قدمًا.
الآن نحن بحاجة إلى العثور على العرض.	العرض هو\(L−2\). العرض هو 12 قدمًا.
الخطوة 6. تحقق. منذ ذلك الحين\(14+12+14+12=52\)، هذا يعمل!
الخطوة 7. أجب على السؤال.	الطول 14 قدمًا والعرض 12 قدمًا.

جرب ذلك\(\PageIndex{23}\)

يقل عرض المستطيل عن الطول بسبعة أمتار. يبلغ محيطها 58 مترًا. ابحث عن الطول والعرض.

إجابة

18 مترًا، 11 مترًا

جرب ذلك\(\PageIndex{24}\)

يزيد طول المستطيل عن العرض بثمانية أقدام. يبلغ محيطه 60 قدمًا. ابحث عن الطول والعرض.

إجابة

19 قدمًا و11 قدمًا

مثال\(\PageIndex{13}\)

يزيد طول المستطيل بأربعة سنتيمترات عن ضعف العرض. يبلغ محيطها 32 سم. ابحث عن الطول والعرض.

الحل

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	الطول والعرض
الخطوة 3. اسم. اختر متغيرًا لتمثيل العرض.
الطول يزيد بأربعة عن ضعف العرض.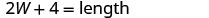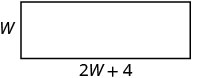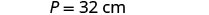
الخطوة 4. ترجم
اكتب الصيغة المناسبة.	\(\quad P=2L+2W\)
استبدل المعلومات المعطاة.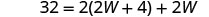
الخطوة 5. حل المعادلة.	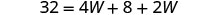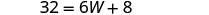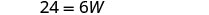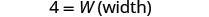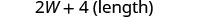12 الطول هو 12 سم.
الخطوة 6. تحقق. \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2\cdot 4} \\ {32} &{=} &{32\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	الطول 12 سم والعرض 4 سم.

جرب ذلك\(\PageIndex{25}\)

يزيد طول المستطيل بمقدار ثمانية أضعاف عن ضعف العرض. المحيط هو 64. ابحث عن الطول والعرض.

إجابة

24، 8

جرب ذلك\(\PageIndex{26}\)

يقل عرض المستطيل بمقدار ستة عن ضعف الطول. المحيط هو 18. ابحث عن الطول والعرض.

إجابة

5، 4

مثال\(\PageIndex{14}\)

يبلغ محيط حوض السباحة المستطيل 150 قدمًا. الطول يزيد بمقدار 15 قدمًا عن العرض. ابحث عن الطول والعرض.

الحل

الخطوة 1. اقرأ المشكلة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.	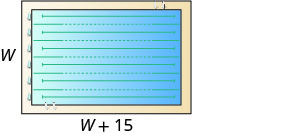\(P=150\)قدم
الخطوة 2. حدد ما تبحث عنه.	طول وعرض حمام السباحة
الخطوة 3. اسم. اختر متغيرًا لتمثيل العرض. الطول يزيد بمقدار 15 قدمًا عن العرض.
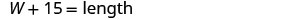الخطوة 4. ترجم
اكتب الصيغة المناسبة.	\(\quad P=2L+2W\)
بديل.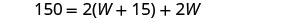
الخطوة 5. حل المعادلة.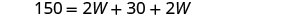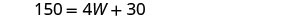
الخطوة 6. تحقق. \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}\)
الخطوة 7. أجب على السؤال.	يبلغ طول المسبح 45 قدمًا والعرض 30 قدمًا.

جرب ذلك\(\PageIndex{27}\)

يبلغ محيط حوض السباحة المستطيل 200 قدم. الطول يزيد بمقدار 40 قدمًا عن العرض. ابحث عن الطول والعرض.

إجابة

70 قدمًا و30 قدمًا

جرب ذلك\(\PageIndex{28}\)

يبلغ طول الحديقة المستطيلة 30 ياردة أكثر من العرض. محيط المبنى هو 300 ياردة. ابحث عن الطول والعرض.

إجابة

90 ياردة و60 ياردة

المفاهيم الرئيسية

• إستراتيجية حل المشكلات لتطبيقات الهندسة
  1. اقرأ المشكلة واجعل كل الكلمات والأفكار مفهومة. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
  2. حدد ما نبحث عنه.
  3. قم بتسمية ما نبحث عنه عن طريق اختيار متغير لتمثيله.
  4. ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
  5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
  6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
  7. أجب على السؤال بجملة كاملة.
• خصائص المثلث لـ △ قياسات
  زاوية ABC:
  • \(m\angle{A}+m\angle{B}+m\angle{C}=180\)
  محيط:
  • \(P=a+b+c\)
  المنطقة:
  • \(A=\frac{1}{2}bh\)، b = القاعدة، h = الارتفاع
  المثلث الأيمن له زاوية واحدة مقدارها 90 درجة.
• نظرية فيثاغورس في أي مثلث قائم الزاوية،\(a^{2} + b^{2} = c^{2}\) أين\(c\) طول الوتر وأطوال الساقين.\(a\)\(b\)
• خصائص المستطيلات
  • تحتوي المستطيلات على أربعة جوانب وأربع زوايا قائمة (90 درجة).
  • أطوال الأضلاع المقابلة متساوية.
  • محيط المستطيل هو مجموع ضعف الطول وضعف العرض:\(P=2L+2W\).
  • مساحة المستطيل هي الطول في العرض:\(A=LW\).