1.6: تصور الكسور
- Page ID
- 200657
في نهاية هذا القسم، ستكون قادرًا على:
- ابحث عن الكسور المتكافئة
- تبسيط الكسور
- اضرب الكسور
- قسّم الكسور
- قم بتبسيط التعبيرات المكتوبة باستخدام شريط الكسر
- ترجمة العبارات إلى التعبيرات ذات الكسور
يمكن العثور على مقدمة أكثر شمولاً للموضوعات التي يتم تناولها في هذا القسم في فصل ما قبل الجبر، الكسور.
ابحث عن الكسور المتكافئة
الكسور هي طريقة لتمثيل أجزاء من الكل. الكسر\(\dfrac{1}{3}\) يعني أنه تم تقسيم الكل إلى 3 أجزاء متساوية وكل جزء هو واحد من الأجزاء الثلاثة المتساوية. انظر الشكل\(\PageIndex{1}\). \(\dfrac{2}{3}\)يُمثِّل الكسر اثنين من ثلاثة أجزاء متساوية. في الكسر\(\dfrac{2}{3}\)، يُطلق على 2 اسم البسط بينما يُطلق على 3 اسم المقام.
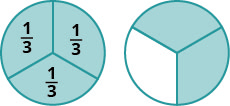
يتم كتابة الكسر وأين\(\dfrac{a}{b}\)\(b\neq 0\) و
- \(a\)هو البسط\(b\) والمقام.
يمثل الكسر أجزاء من الكل. المقام\(b\) هو عدد الأجزاء المتساوية التي تم تقسيم الكل إليها،\(a\) ويشير البسط إلى عدد الأجزاء المضمنة.
إذا تم تقطيع فطيرة كاملة إلى 6 قطع وأكلنا جميع القطع الست، أكلنا\(\dfrac{6}{6}\) قطعًا، أو بعبارة أخرى، فطيرة كاملة.
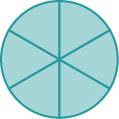
لذا\(\dfrac{6}{6}=1\). هذا يقودنا إلى خاصية واحدة تخبرنا أن أي رقم، باستثناء الصفر، مقسومًا على نفسه\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
أي رقم، باستثناء الصفر، مقسومًا على نفسه هو واحد.
سيساعدك القيام بنشاط الرياضيات المتلاعبة «الكسور المكافئة لواحد» على تطوير فهم أفضل للكسور المكافئة لواحد.
إذا تم قطع الفطيرة إلى 6 قطع وأكلنا كل 6\(\dfrac{6}{6}\) قطع، أكلنا قطعًا، أو بعبارة أخرى، فطيرة واحدة كاملة. إذا تم تقطيع الفطيرة إلى 8 قطع وأكلنا كل 8\(\dfrac{8}{8}\) قطع، أكلنا قطعًا أو فطيرة واحدة كاملة. أكلنا نفس الكمية - فطيرة واحدة كاملة.
الكسور\(\dfrac{6}{6}\)\(\dfrac{8}{8}\) ولها نفس القيمة، 1، وبالتالي تسمى الكسور المتكافئة. الكسور المتكافئة هي الكسور التي لها نفس القيمة.
دعونا نفكر في البيتزا هذه المرة. \(\PageIndex{3}\)يُظهر الشكل صورتين: بيتزا واحدة على اليسار، مقطعة إلى قطعتين متساويتين، وبيتزا ثانية بنفس الحجم، مقطعة إلى ثماني قطع على اليمين. هذه طريقة لإظهار\(\dfrac{1}{2}\) ما يعادل\(\dfrac{4}{8}\). بمعنى آخر، إنها كسور مكافئة.
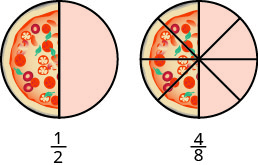
الكسور المتكافئة هي الكسور التي لها نفس القيمة.
كيف يمكننا استخدام الرياضيات للتغيير\(\dfrac{1}{2}\) إليها\(\dfrac{4}{8}\)؟ كيف يمكننا أخذ بيتزا مقطعة إلى قطعتين وقطعها إلى 8 قطع؟ يمكننا قطع كل قطعة من القطعتين الأكبر حجمًا إلى 4 قطع أصغر! سيتم بعد ذلك تقطيع البيتزا بأكملها إلى 88 قطعة بدلاً من قطعتين فقط. رياضياً، ما وصفناه يمكن كتابته على هذا النحو\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). انظر الشكل\(\PageIndex{4}\).
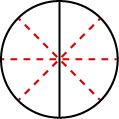
يؤدي هذا النموذج إلى الخاصية التالية:
إذا كانت الأرقام\(a,b,c\) هي المكان\(b\neq 0, c\neq 0\)، إذن
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
إذا قطعنا البيتزا بشكل مختلف، يمكننا الحصول على
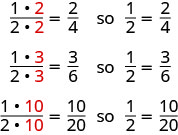
لذلك، نقول\(\dfrac{1}{2}\)،\(\dfrac{2}{4}\)\(\dfrac{3}{6}\)،\(\dfrac{10}{20}\) وهي كسور مكافئة.
سيساعدك القيام بنشاط الرياضيات المتلاعبة «الكسور المتكافئة» على تطوير فهم أفضل لما يعنيه عندما يتساوى كسران.
أوجد ثلاثة كسور مكافئة لـ\(\dfrac{2}{5}\).
- إجابة
-
لإيجاد كسر مكافئ له\(\dfrac{2}{5}\)، نضرب البسط والمقام في نفس العدد. يمكننا اختيار أي رقم، باستثناء الصفر. دعونا نضربهم في 2، 3، ثم 5.
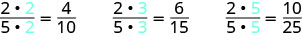
-
لذلك\(\dfrac{4}{10}\)،\(\dfrac{6}{15}\)،،\(\dfrac{10}{25}\) وتعادل\(\dfrac{2}{5}\).
أوجد ثلاثة كسور مكافئة لـ\(\dfrac{3}{5}\).
- إجابة
-
\(\dfrac{6}{10}\)،\(\dfrac{9}{15}\)،\(\dfrac{12}{20}\)؛ قد تختلف الإجابات
أوجد ثلاثة كسور مكافئة لـ\(\dfrac{4}{5}\).
- إجابة
-
\(\dfrac{8}{10}\)،\(\dfrac{12}{15}\)،\(\dfrac{16}{20}\)؛ قد تختلف الإجابات
تبسيط الكسور
يعتبر الكسر مبسطًا إذا لم تكن هناك عوامل مشتركة، بخلاف 1، في البسط والمقام.
على سبيل المثال،
- \(\dfrac{2}{3}\)تم تبسيطه نظرًا لعدم وجود عوامل مشتركة لـ 2 و 3.
- \(\dfrac{10}{15}\)لم يتم تبسيطه لأن 5 هو عامل مشترك بين 10 و 15.
يعتبر الكسر مبسطًا إذا لم تكن هناك عوامل مشتركة في البسط والمقام.
تعني عبارة تقليل الكسر تبسيط الكسر. نقوم بتبسيط الكسر أو تقليله عن طريق إزالة العوامل المشتركة للبسط والمقام. لا يتم تبسيط الكسر حتى تتم إزالة جميع العوامل الشائعة. إذا كان التعبير يحتوي على كسور، فلن يتم تبسيطه تمامًا حتى يتم تبسيط الكسور.
في التمرين\(\PageIndex{4}\)، استخدمنا خاصية الكسور المتكافئة لإيجاد الكسور المتكافئة. الآن سنستخدم خاصية الكسور المتكافئة في الاتجاه المعاكس لتبسيط الكسور. يمكننا إعادة كتابة الخاصية لإظهار كلا النموذجين معًا.
إذا كانت\(a,b,c\) الأرقام حيث\(b\neq 0,c\neq 0\)،
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
قم بالتبسيط:\(-\dfrac{32}{56}\)
- إجابة
-
\(-\dfrac{32}{56}\) أعد كتابة البسط والمقام موضحًا العوامل المشتركة. \(-\dfrac{4\cdot 8}{7\cdot 8}\) قم بالتبسيط باستخدام خاصية الكسور المتكافئة. \(-\dfrac{4}{7}\) لاحظ أنه تم تبسيط الكسر\(-\dfrac{4}{7}\) نظرًا لعدم وجود عوامل مشتركة أخرى.
قم بالتبسيط:\(-\dfrac{42}{54}\)
- إجابة
-
\(-\dfrac{7}{9}\)
قم بالتبسيط:\(-\dfrac{42}{54}\)
- إجابة
-
\(-\dfrac{5}{9}\)
في بعض الأحيان قد لا يكون من السهل العثور على العوامل المشتركة للبسط والمقام. وعند حدوث ذلك، فإن الفكرة الجيدة هي حساب البسط والمقام إلى عدد أولي s، ثم تقسيم العوامل المشتركة باستخدام خاصية الكسور المتكافئة.
قم بالتبسيط:\(-\dfrac{210}{385}\)
- إجابة
-



قم بالتبسيط:\(-\dfrac{69}{120}\)
- إجابة
-
\(-\dfrac{23}{40}\)
قم بالتبسيط:\(-\dfrac{120}{192}\)
- إجابة
-
\(-\dfrac{5}{8}\)
نلخص الآن الخطوات التي يجب اتباعها لتبسيط الكسور.
- أعد كتابة البسط والمقام لإظهار العوامل المشتركة.
إذا لزم الأمر، قم بحساب البسط والمقام في أعداد أولية أولاً. - قم بتبسيط استخدام خاصية الكسور المتكافئة من خلال تقسيم العوامل المشتركة.
- اضرب أي عوامل متبقية، إذا لزم الأمر.
قم بالتبسيط:\(\dfrac{5x}{5y}\)
- إجابة
-
\(\dfrac{5x}{5y}\) أعد كتابة عرض العوامل المشتركة، ثم قسّم العوامل المشتركة. 
قم بالتبسيط. \(\dfrac{x}{y}\)
قم بالتبسيط:\(\dfrac{7x}{7y}\)
- إجابة
-
\(\dfrac{x}{y}\)
قم بالتبسيط:\(\dfrac{3a}{3b}\)
- إجابة
-
\(\dfrac{a}{b}\)
ضرب الكسور
يجد العديد من الأشخاص أن ضرب الكسور وقسمتها أسهل من جمع الكسور وطرحها. لذلك سنبدأ بالضرب الجزئي.
سيساعدك القيام بنشاط الرياضيات المتلاعبة «ضرب الكسور النموذجي» على تطوير فهم أفضل لضرب الكسور.سنستخدم نموذجًا لتوضيح كيفية ضرب كسرين ولمساعدتك على تذكر الإجراء. دعونا نبدأ بـ\(\dfrac{3}{4}\).

الآن سننطلق\(\dfrac{1}{2}\)\(\dfrac{3}{4}\).

لاحظ أن الكل مقسم الآن إلى 8 أجزاء متساوية. لذا\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
لضرب الكسور، نضرب البسط ونضرب المقامات.
إذا كانت الأرقام\(d\) موجودة\(a,b,c\)\(b\neq 0\) وأين\(d\neq 0\)، ثم
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
لضرب الكسور، اضرب البسط واضرب المقامات.
عند ضرب الكسور، لا تزال خصائص الأرقام الموجبة والسالبة سارية بالطبع. من الجيد تحديد علامة المنتج كخطوة أولى. في التمرين\(\PageIndex{13}\)، سنضرب السالب والإيجابي، وبالتالي سيكون المنتج سلبيًا.
اضرب:\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- إجابة
-
الخطوة الأولى هي العثور على علامة المنتج. نظرًا لاختلاف العلامات، يكون المنتج سلبيًا.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
اضرب:\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- إجابة
-
\(-\dfrac{4}{21}\)
اضرب:\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- إجابة
-
\(-\dfrac{3}{16}\)
عند ضرب كسر في عدد صحيح، قد يكون من المفيد كتابة العدد الصحيح ككسر. يمكن كتابة أي عدد صحيح، a، كـ\(\dfrac{a}{1}\). لذلك، على سبيل المثال،\(3 = \dfrac{3}{1}\).
اضرب:\(-\dfrac{12}{5}(-20x)\)
- إجابة
-
حدد علامة المنتج. العلامات هي نفسها، لذا فإن المنتج إيجابي.
\(-\dfrac{12}{5}(-20x)\) اكتب\(20x\) ككسر. \(\dfrac{12}{5}(\dfrac{20x}{1})\) اضرب. أعد الكتابة\(20\) لإظهار العامل المشترك\(5\) وتقسيمه. 
قم بالتبسيط. \(48x\)
اضرب:\(\dfrac{11}{3}(-9a)\)
- إجابة
-
\(-33a\)
اضرب:\(\dfrac{13}{7}(-14b)\)
- إجابة
-
\(-26b\)
قسمة الكسور
الآن بعد أن عرفنا كيفية ضرب الكسور، أصبحنا مستعدين تقريبًا للقسمة. قبل أن نتمكن من القيام بذلك، نحتاج إلى بعض المفردات.
يُوجد مقلوب الكسر بقلب الكسر ووضع البسط في المقام والمقام في البسط. المعاملة بالمثل\(\dfrac{2}{3}\) هي\(\dfrac{3}{2}\).
لاحظ ذلك\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). عدد وضربه العكسي إلى\(1\).
للحصول على ناتج موجب\(1\) عند ضرب رقمين، يجب أن تحتوي الأرقام على نفس العلامة. لذلك يجب أن تحمل الرسائل المتبادلة نفس العلامة.
أما المعاملة بالمثل\(-\dfrac{10}{7}\) فهي\(-\dfrac{7}{10}\)، منذ ذلك الحين\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
المعاملة بالمثل\(\dfrac{a}{b}\) هي\(\dfrac{b}{a}\).
عدد وضربه العكسي في واحد\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
سيساعدك القيام بنشاط الرياضيات المتلاعبة «قسم الكسر النموذجي» على تطوير فهم أفضل لتقسيم الكسور.
لتقسيم الكسور، نضرب الكسر الأول في مقلوب الثاني.
إذا كانت الأرقام\(d\) موجودة\(a,b,c\)\(b\neq 0, c\neq 0\) وأين\(d\neq 0\)، ثم
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
لتقسيم الكسور، نضرب الكسر الأول في مقلوب الثاني.
نحن بحاجة\(d\neq 0\) إلى القول\(b\neq 0, c\neq 0\) والتأكد من أننا لا نقسم على الصفر!
قسّم:\(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- إجابة
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
قسّم:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- إجابة
-
\(-\dfrac{21}{5p}\)
قسّم:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- إجابة
-
\(-\dfrac{15}{8q}\)
ابحث عن حاصل القسمة:
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- إجابة
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) للقسمة، اضرب الكسر الأول في مقلوب الثاني. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) حدد علامة المنتج، ثم اضرب.. \(\dfrac{7\cdot 27}{18\cdot 14}\) أعد كتابة عرض العوامل المشتركة. 
قم بإزالة العوامل المشتركة. \(\dfrac{3}{2\cdot 2}\) قم بالتبسيط. \(\dfrac{3}{4}\)
ابحث عن حاصل القسمة:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- إجابة
-
\(\dfrac{4}{15}\)
ابحث عن حاصل القسمة:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- إجابة
-
\(\dfrac{2}{3}\)
هناك عدة طرق لتذكر الخطوات التي يجب اتخاذها لضرب الكسور أو تقسيمها. إحدى الطرق هي تكرار المكالمات لنفسك. إذا قمت بذلك في كل مرة تقوم فيها بتمرين، فسوف يتم حفظ الخطوات.
- «لضرب الكسور، اضرب البسط واضرب المقامات.»
- «لتقسيم الكسور، اضرب الكسر الأول في مقلوب الثاني.»
هناك طريقة أخرى تتمثل في وضع مثالين في الاعتبار:
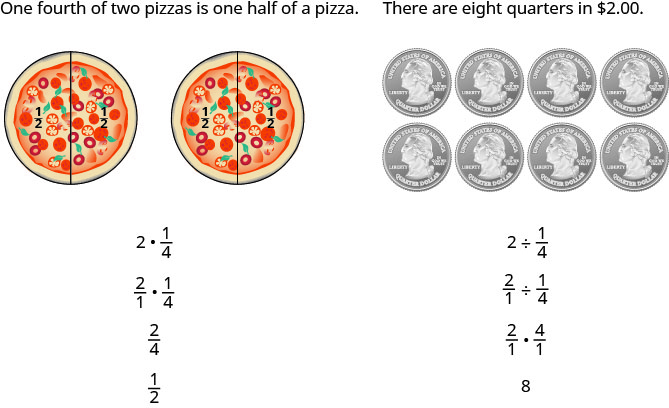
تحتوي البسط أو القواسم لبعض الكسور على الكسور نفسها. يسمى الكسر الذي يكون فيه البسط أو المقام كسرًا بالكسر المركب.
الكسر المركب هو كسر يحتوي فيه البسط أو المقام على كسر.
بعض الأمثلة على الكسور المعقدة هي:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
لتبسيط الكسر المعقد، نتذكر أن شريط الكسر يعني القسمة. على سبيل المثال،\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) يعني الكسر المعقد\(\dfrac{3}{4} \div \dfrac{5}{8}\).
قم بالتبسيط:\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- إجابة
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) أعد الكتابة كقسم. \(\dfrac{3}{4} \div \dfrac{5}{8}\) اضرب الكسر الأول في مقلوب الثاني. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) اضرب. \(\dfrac{3\cdot 8}{4\cdot 5}\) ابحث عن العوامل المشتركة. 
قسّم العوامل المشتركة وقم بتبسيطها. \(\dfrac{6}{5}\)
قم بالتبسيط:\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- إجابة
-
\(\dfrac{4}{5}\)
قم بالتبسيط:\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- إجابة
-
\(\dfrac{11}{14}\)
قم بالتبسيط:\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- إجابة
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) أعد الكتابة كقسم. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) اضرب الكسر الأول في مقلوب الثاني. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) اضرب. \(\dfrac{x\cdot 6}{2\cdot xy}\) ابحث عن العوامل المشتركة. 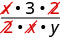
قسّم العوامل المشتركة وقم بتبسيطها. \(\dfrac{3}{y}\)
قم بالتبسيط:\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- إجابة
-
\(\dfrac{3}{4b}\)
قم بالتبسيط:\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- إجابة
-
\(\dfrac{4}{q}\)
قم بتبسيط التعبيرات باستخدام شريط الكسر
الخط الذي يفصل البسط عن المقام في الكسر يسمى شريط الكسر. يعمل شريط الكسر كرمز تجميع. ثم يخبرنا ترتيب العمليات بتبسيط البسط ثم المقام. ثم نقسم.
لتبسيط التعبير\(\dfrac{5 - 3}{7 + 1}\)، نقوم أولاً بتبسيط البسط والمقام بشكل منفصل. ثم نقسم.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- قم بتبسيط التعبير في البسط. قم بتبسيط التعبير في المقام.
- قم بتبسيط الكسر.
قم بالتبسيط:\(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- إجابة
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
قم بالتبسيط:\(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- إجابة
-
\(-\dfrac{3}{4}\)
قم بالتبسيط:\(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- إجابة
-
\(-\dfrac{5}{3}\)
أين تذهب العلامة السالبة في الكسر؟ عادةً ما تكون العلامة السالبة أمام الكسر، لكنك سترى أحيانًا كسرًا ببسط سالب، أو أحيانًا بمقام سالب. تذكر أن الكسور تمثل القسمة. عندما تكون علامات البسط والمقام مختلفة، يكون حاصل القسمة سالبًا.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
للحصول على أي أرقام إيجابية\(a\) و\(b\)،
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
قم بالتبسيط:\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- إجابة
-
يعمل شريط الكسر كرمز تجميع. لذا قم بتبسيط البسط والمقام بشكل منفصل.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
قم بالتبسيط:\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- إجابة
-
\(4\)
قم بالتبسيط:\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- إجابة
-
\(2\)
ترجمة العبارات إلى التعبيرات ذات الكسور
الآن بعد أن قمنا ببعض الأعمال مع الكسور، نحن على استعداد لترجمة العبارات التي من شأنها أن تؤدي إلى تعبيرات ذات كسور.
غالبًا ما تستخدم الكلمات الإنجليزية حاصل القسمة والنسبة لوصف الكسور. تذكر أن «حاصل القسمة» يعني القسمة. حاصل القسمة aa و bb هو النتيجة التي نحصل عليها من القسمة\(a\) على\(b\) أو\(\dfrac{a}{b}\).
ترجم العبارة الإنجليزية إلى تعبير جبري: حاصل فرق\( m\) و\(n\) و\(p\).
- إجابة
-
نحن نبحث عن حاصل الفرق بين\(m\) و\(n\)، و\(p\).. هذا يعني أننا نريد تقسيم الفرق بين\(m\) و\(n\) و و\(p\).
\[\dfrac{m - n}{p}\]
ترجم العبارة الإنجليزية إلى تعبير جبري: حاصل فرق\(a\) و\(b\) و\(cd\).
- إجابة
-
\(\dfrac{a - b}{cd}\)
ترجم العبارة الإنجليزية إلى تعبير جبري: حاصل مجموع\(p\) و\(q\) و\(r\).
- إجابة
-
\(\dfrac{p + q}{r}\)
المفاهيم الرئيسية
- خاصية الكسور المتكافئة: إذا كانت الأرقام\(a, b, c\) هي أين ثم\(b\neq 0, c\neq 0\)
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) و\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - قسم الكسر: إذا كانت الأرقام\(d\) موجودة\(a, b, c\)\(b\neq 0, c\neq 0\) وأين\(d \neq 0\) ثم\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). لتقسيم الكسور، اضرب الكسر الأول في مقلوب الثاني.
- ضرب الكسور: إذا كانت الأرقام\(d\) موجودة\(a,b,c\) وأين\(b\neq 0, d\neq 0\)، إذن\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). لضرب الكسور، اضرب البسط واضرب المقامات.
- وضع العلامة السالبة في الكسر: لأي أرقام موجبة\(a\) و\(b\)،\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- خاصية واحد:\(\dfrac{a}{a} = 1\)؛ أي رقم، باستثناء الصفر، مقسومًا على نفسه هو واحد.
- تبسيط الكسر
- أعد كتابة البسط والمقام لإظهار العوامل المشتركة. إذا لزم الأمر، قم بحساب البسط والمقام في أعداد أولية أولاً.
- قم بتبسيط استخدام خاصية الكسور المتكافئة من خلال تقسيم العوامل المشتركة.
- اضرب أي عوامل متبقية.
- قم بتبسيط تعبير باستخدام شريط الكسر
- قم بتبسيط التعبير في البسط. قم بتبسيط التعبير في المقام.
- قم بتبسيط الكسر.
مسرد المصطلحات
- كسر معقد
- الكسر المركب هو كسر يحتوي فيه البسط أو المقام على كسر.
- القاسم
- المقام هو القيمة الموجودة في الجزء السفلي من الكسر التي تشير إلى عدد الأجزاء المتساوية التي تم تقسيم الكل إليها.
- الكسور المكافئة
- الكسور المتكافئة هي الكسور التي لها نفس القيمة.
- كسر
- يتم كتابة كسر\(\frac{a}{b}\)\(b\neq 0\)، حيث يكون a هو البسط و b هو المقام. يمثل الكسر أجزاء من الكل. المقام b هو عدد الأجزاء المتساوية التي تم تقسيم الكل إليها، ويشير البسط aa إلى عدد الأجزاء المضمنة.
- عداد
- البسط هو القيمة الموجودة في الجزء العلوي من الكسر التي تشير إلى عدد أجزاء الكل المضمنة.
- المعاملة بالمثل
- المعاملة بالمثل\(\frac{a}{b}\) هي\(\frac{b}{a}\). عدد وضربه في واحد:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- كسر مبسط
- يعتبر الكسر مبسطًا إذا لم تكن هناك عوامل مشتركة في البسط والمقام.


