1.6E: تمارين
- Page ID
- 200673
الممارسة تجعل من الكمال
ابحث عن الكسور المتكافئة
في التمارين التالية، أوجد ثلاثة كسور مكافئة للكسر المعطى. اعرض عملك باستخدام الأشكال أو الجبر.
\(\dfrac{3}{8}\)
- إجابة
-
\(\dfrac{6}{16}\)،\(\dfrac{9}{24}\)،\(\dfrac{12}{32}\)، قد تختلف الإجابات
\(\dfrac{5}{8}\)
\(\dfrac{5}{9}\)
- إجابة
-
\(\dfrac{10}{18}\)،\(\dfrac{15}{27}\)،\(\dfrac{20}{36}\)، قد تختلف الإجابات
\(\dfrac{1}{8}\)
تبسيط الكسور
في التمارين التالية، قم بالتبسيط.
\(-\dfrac{40}{88}\)
- إجابة
-
\(-\dfrac{5}{11}\)
\(-\dfrac{63}{99}\)
\(-\dfrac{108}{63}\)
- إجابة
-
\(-\dfrac{12}{7}\)
\(-\dfrac{104}{48}\)
\(\dfrac{120}{252}\)
- إجابة
-
\(\dfrac{10}{21}\)
\(\dfrac{182}{294}\)
\(-\dfrac{3x}{12y}\)
- إجابة
-
\(-\dfrac{x}{4y}\)
\(-\dfrac{4x}{32y}\)
\(\dfrac{14x^{2}}{21y}\)
- إجابة
-
\(\dfrac{2x^{2}}{3y}\)
\(\dfrac{24a}{32b^{2}}\)
ضرب الكسور
في التمارين التالية، اضرب.
\(\dfrac{3}{4}\cdot \dfrac{9}{10}\)
- إجابة
-
\(\dfrac{27}{40}\)
\(\dfrac{4}{5}\cdot \dfrac{2}{7}\)
\(-\dfrac{2}{3}\cdot -\dfrac{3}{8}\)
- إجابة
-
\(\dfrac{1}{4}\)
\(-\dfrac{3}{4}\left(-\dfrac{4}{9}\right)\)
\(-\dfrac{5}{9}\cdot \dfrac{3}{10}\)
- إجابة
-
\(-\dfrac{1}{6}\)
\(-\dfrac{3}{8}\cdot \dfrac{4}{15}\)
\(\left(-\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)
- إجابة
-
\(-\dfrac{21}{50}\)
\(\left(-\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)
\(\left(-\dfrac{63}{84}\right)\left(-\dfrac{44}{90}\right)\)
- إجابة
-
\(\dfrac{11}{30}\)
\(\left(-\dfrac{63}{60}\right)\left(-\dfrac{40}{88}\right)\)
\(4\cdot \dfrac{5}{11}\)
- إجابة
-
\(\dfrac{20}{11}\)
\(5\cdot \dfrac{8}{3}\)
\(\dfrac{3}{7}\cdot 21n\)
- إجابة
-
9 متر
\(\dfrac{5}{6}\cdot 30m\)
\(-8\cdot\dfrac{17}{4}\)
- إجابة
-
−34
\((-1)\left(-\dfrac{6}{7}\right)\)
قسمة الكسور
في التمارين التالية، قسّم.
\(\dfrac{3}{4}\div \dfrac{2}{3}\)
- إجابة
-
\(\dfrac{9}{8}\)
\(\dfrac{4}{5}\div \dfrac{3}{4}\)
\(-\dfrac{7}{9}\div \left(-\dfrac{7}{4}\right)\)
- إجابة
-
1
\(-\dfrac{5}{6}\div \left(-\dfrac{5}{6}\right)\)
\(\dfrac{3}{4}\div \dfrac{x}{11}\)
- إجابة
-
\(\dfrac{33}{4x}\)
\(\dfrac{2}{5}\div \dfrac{y}{9}\)
\(\dfrac{5}{18}\div -\dfrac{15}{24}\)
- إجابة
-
\(-\dfrac{4}{9}\)
\(\dfrac{7}{18}\div \left(-\dfrac{14}{27}\right)\)
\(\dfrac{8u}{15} \div \dfrac{12v}{25}\)
- إجابة
-
\(\dfrac{10u}{9v}\)
\(\dfrac{12r}{25}\div \dfrac{18s}{35}\)
\(-5\div \dfrac{1}{2}\)
- إجابة
-
-10
\(-3\div \dfrac{1}{4}\)
\(\dfrac{3}{4}\div (-12)\)
- إجابة
-
\(\dfrac{1}{16}\)
\(-15\div -\dfrac{5}{3}\)
في التمارين التالية، قم بالتبسيط.
\(\dfrac{-\dfrac{8}{21}}{\dfrac{12}{35}}\)
- إجابة
-
\(-\dfrac{10}{9}\)
\(\dfrac{-\dfrac{9}{16}}{\dfrac{33}{40}}\)
\(\dfrac{-\dfrac{4}{5}}{2}\)
- إجابة
-
\(-\dfrac{2}{5}\)
\(\dfrac{5}{\dfrac{3}{10}}\)
\(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)
- إجابة
-
\(\dfrac{2m}{3n}\)
\(\dfrac{-\dfrac{3}{8}}{-\dfrac{y}{12}}\)
قم بتبسيط التعبيرات المكتوبة باستخدام شريط الكسر
في التمارين التالية، قم بالتبسيط.
\(\dfrac{22 + 3}{10}\)
- إجابة
-
\(\dfrac{5}{2}\)
\(\dfrac{19 - 4}{6}\)
\(\dfrac{48}{24 - 15}\)
- إجابة
-
\(\dfrac{16}{3}\)
\(\dfrac{46}{4 + 4}\)
\(\dfrac{-6 + 6}{8 + 4}\)
- إجابة
-
0
\(\dfrac{-6 + 3}{17 - 8}\)
\(\dfrac{4\cdot 3}{6\cdot 6}\)
- إجابة
-
\(\dfrac{1}{3}\)
\(\dfrac{6\cdot 6}{9\cdot 2}\)
\(\dfrac{4^{2} - 1}{25}\)
- إجابة
-
\(\dfrac{3}{5}\)
\(\dfrac{7^{2} + 1}{60}\)
\(\dfrac{8\cdot 3 + 2\cdot 9}{14 + 3}\)
- إجابة
-
\(2\dfrac{8}{17}\)
\(\dfrac{9\cdot 6 - 4\cdot 7}{22 + 3}\)
\(\dfrac{5\cdot 6 - 3\cdot 4}{4\cdot 5 -2\cdot 3}\)
- إجابة
-
\(\dfrac{9}{7}\)
\(\dfrac{8\cdot 9 - 7\cdot 6}{5\cdot 6 - 9\cdot 2}\)
\(\dfrac{5^{2} - 3^{2}}{3 - 5}\)
- إجابة
-
\(-8\)
\(\dfrac{6^{2} - 4^{2}}{4 - 6}\)
\(\dfrac{7\cdot 4 - 2(8 - 5)}{9\cdot 3 - 3\cdot 5}\)
- إجابة
-
\(\dfrac{11}{6}\)
\(\dfrac{9\cdot 7 - 3(12- 8)}{8\cdot 7- 6\cdot 6}\)
\(\dfrac{9(8-2)-3(15-7)}{6(7-1) - 3(17-9)}\)
- إجابة
-
\(\dfrac{5}{2}\)
\(\dfrac{8(9-2) - 4(14 - 9)}{7(8-3)-3(16 -9)}\)
ترجمة العبارات إلى التعبيرات ذات الكسور
في التمارين التالية، ترجم كل عبارة إنجليزية إلى تعبير جبري.
حاصل قسمة\(r\) ومجموع\(s\) و\(10\)
- إجابة
-
\(\dfrac{r}{s + 10}\)
حاصل القسمة\(A\) والفرق بين\(3\) و\(B\)
حاصل قسمة الفرق بين\(x\) و\(y\)، و\(−3\)
- إجابة
-
\(\dfrac{x - y}{-3}\)
حاصل قسمة مجموع\(m\) و\(n\)، و\(4q\)
الرياضيات اليومية
الخبز. تتطلب وصفة رقائق الكوكيز بالشوكولاتة\(\frac{3}{4}\) كوبًا من السكر البني. تريد إيميلدا مضاعفة الوصفة.
- ما مقدار السكر البني الذي ستحتاجه إيميلدا؟ أظهر الحساب الخاص بك.
- عادة ما تأتي أكواب القياس في مجموعات من\(\frac{1}{4}\),\(\frac{1}{3}\),\(\frac{1}{2}\),\(1\) وأكواب. ارسم مخططًا لإظهار طريقتين مختلفتين يمكن لـ Imelda من خلالها قياس السكر البني اللازم لمضاعفة وصفة الكعكة.
- إجابة
-
- \(1\frac{1}{2}\)أكواب
- سوف تتنوع الإجابات
الخبز. تقوم نينا بإعداد 4 أواني من الحلوى لتقديمها بعد حفل موسيقي. لكل مقلاة، تحتاج إلى\(\frac{2}{3}\) كوب من الحليب المكثف.
- ما مقدار الحليب المكثف الذي ستحتاجه نينا؟ أظهر الحساب الخاص بك.
- عادة ما تأتي أكواب القياس في مجموعات من\(\frac{1}{4}\),\(\frac{1}{3}\),\(\frac{1}{2}\),\(1\) وأكواب. ارسم مخططًا لإظهار طريقتين مختلفتين يمكن لنينا من خلالهما قياس الحليب المكثف اللازم\(4\) لأواني الحلوى.
قامت شركة Partions Don بشراء حزمة كبيرة من الحلوى تزن\(5\) رطلاً. يريد بيع الحلوى في أكياس صغيرة تحتوي على\(\frac{1}{4}\) رطل. كم عدد أكياس الحلوى الصغيرة التي يمكن أن يملأها من العبوة السائبة؟
- إجابة
-
\(20\)حقائب
تحتوي Kristen Partings على\(\frac{3}{4}\) ياردات من الشريط الذي تريد قطعه إلى أجزاء\(6\) متساوية لصنع شرائط شعر\(6\) لدمى ابنتها. كم سيكون طول شريط شعر كل دمية؟
تمارين الكتابة
أراد رافائيل طلب نصف بيتزا متوسطة في مطعم. أخبره النادل أنه يمكن تقطيع البيتزا المتوسطة إلى\(6\)\(8\) شرائح. هل يفضل\(3\) الخروج من\(6\) الشرائح أم\(4\) خارج\(8\) الشرائح؟ أجاب رافائيل أنه نظرًا لأنه لم يكن جائعًا جدًا، فإنه يفضل\(3\) عدم تناول\(6\) الشرائح. اشرح ما هو الخطأ في منطق رافائيل.
- إجابة
-
قد تختلف الإجابات
أعط مثالاً من الحياة اليومية يوضح كيف يحدث\(\dfrac{1}{2}\cdot \dfrac{2}{3}\) ذلك\(\dfrac{1}{3}\).
اشرح كيف تجد مقلوب الكسر.
- إجابة
-
قد تختلف الإجابات
اشرح كيفية العثور على المعاملة بالمثل لرقم سالب.
فحص ذاتي
ⓐ بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم إتقانك لأهداف هذا القسم.
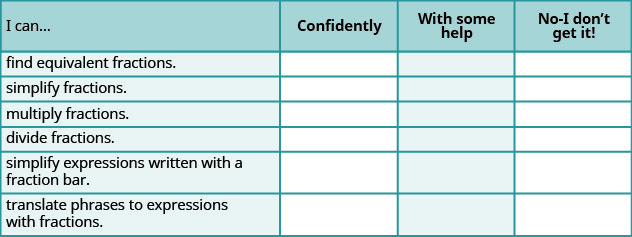
ⓑ بعد الاطلاع على قائمة التحقق، هل تعتقد أنك مستعد جيدًا للقسم التالي؟ لماذا أو لماذا لا؟


