4.7: הוספת מומנטה זוויתית
- Page ID
- 207182
שקול מערכת בעלת שתי מומנטות זוויתיות, למשל אלקטרון באטום מימן בעל תנע זוויתי מסלולי וגם ספין. למרחב ה- ket למומנטום זוויתי יחיד יש בסיס אורתונורמלי \(|j,m\rangle\) ולכן עבור שתי מומנטות זוויתיות בסיס אורתונורמלי ברור הוא קבוצת קלפי המוצר הישירים. \(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) מה זה אומר בדיוק? נניח שלמומנטום הזוויתי הראשון \(\vec{J}_1\) יש גודל\(\vec{J}^2_1=\hbar^2j_1(j_1+1)\), והוא נמצא במצב\(\sum_{m_1=-j_1}^{j_1}\alpha_{m_1}|j_1,m_1\rangle\), ובדומה המומנטום הזוויתי השני \(\vec{J}_2\) נמצא במצב\(\sum_{m_2=-j_2}^{j_2}\beta_{m_2}|j_2,m_2\rangle\). ככל הנראה משרעת ההסתברות למציאת הסיבוב הראשון במצב \(m_1\) ובו זמנית השנייה \(m_2\) היא\(\alpha_{m_1}\beta_{m_2}\), ואנו מציינים מצב זה על ידי. \(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) כיצד להתמודד עם חללי המוצרים הישירים הללו יתברר בבחינת דוגמאות ספציפיות, כפי שאנו עושים להלן, החל משני ספינים חצי.
כעת סכום שתי המומנטה הזוויתית \(\vec{J}=\vec{J}_1+\vec{J}_2\) הוא עצמו תנע זוויתי, הפועל בחלל עם בסיס \(|j,m\rangle\) מלא. זה קל להוכיח: המרכיבים של \(\vec{J}_1\) לספק\([J_{1i},J_{1j}]=i\hbar \varepsilon_{ijk}J_{1k}\), ובאופן דומה עבור הרכיבים של\(\vec{J}_2\). מרכיבי \(\vec{J}_1\) הנסיעה עם המרכיבים של, כמובן\(\vec{J}_2\), שממנו יוצא מיד שמרכיבי הווקטור של \(\vec{J}=\vec{J}_1+\vec{J}_2\) אכן מצייתים ליחסי הקומוטציה של המומנטום הזוויתי: ונזכרים כי יחסי ההחלפה הספיקו כדי לקבוע את קבוצות הערכים העצמיים המותרים. נוכיח מאוחר יותר שהמצבים העצמיים \(|j,m\rangle\) של \(\vec{J}^2,\vec{J}_z\) הם בסיס שלם למרחב התוצר של החלקים העצמיים של \(\vec{J}^2_1,\; \vec{J}^2_2,\; J_{1z},\; J_{2z}\) - כדי לבסס זאת, עלינו למצוא תחילה את הערכים המותרים האפשריים של המספר הקוונטי הכולל של המומנטום הזוויתי. \(j\)
כאן יש לנו, אם כן, שני בסיסים אורתונורמליים שונים למה שהוא ככל הנראה אותו מרחב וקטורי. ביישומים מעשיים מתברר לעתים קרובות שעלינו לתרגם מאחד הבסיסים הללו לשני. המשימה הנוכחית שלנו היא לבנות את השינוי המתאים: אנו משיגים זאת על ידי מציאת המקדמים של כל אחד \(|j,m\rangle\) \(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) בבסיס. אלה נקראים מקדמי קלבש-גורדן.
נבנה בהדרגה, החל מהוספת שני סיבובים חצי, ואז סיבוב חצי עם תנע זוויתי מסלולי, סוף סוף שתי מומנטה זוויתית כללית.
הוספת שני ספינים: מדינות הבסיס ומפעילי הספין
הדוגמה היסודית ביותר למערכת בעלת שתי מומנטות זוויתיות היא אטום המימן במצבו הקרקעי. המומנטום הזוויתי המסלולי הוא אפס, לאלקטרון יש תנע זוויתי ספין\(\frac{1}{2}\hbar\), ולפרוטון יש ספין\(\frac{1}{2}\hbar\).
למרחב המצבים האפשריים של ספין האלקטרונים יש את שני מוטות הבסיס\(|\downarrow \rangle_e\), (כתוב גם באופן שונה כ\(|+\rangle\),\(|-\rangle\);,\(\dbinom{0}{1}\); \(\dbinom{1}{0}\)\(\chi +\),\(\chi -!\)) הבסיס של פרוטון ספין kets הם\(|\downarrow \rangle_p\), \(|\uparrow \rangle_p\) ולכן המצבים האפשריים של המערכת המשולבת הם kets במרחב המוצר הישיר שיש לו בסיס של ארבעה kets: \(|\uparrow \rangle_e\)
\[ |\uparrow_e\uparrow_p\rangle ,\; |\uparrow_e\downarrow_p\rangle ,\; |\downarrow_e\uparrow_p\rangle ,\; |\downarrow_e\downarrow_p\rangle \label{4.7.1}\]
שימוש \(|\uparrow_e\uparrow_p\rangle\) כקיצור עבור\(|\uparrow \rangle_e\otimes |\uparrow \rangle_p\).
שים לב כאן שכתבנו את הקאטס ב"סדר אלפביתי "עם \(\uparrow\) האות הראשונה, \(\downarrow\) כשנייה. כלומר, כתבנו תחילה את כל הקלפים שיש להם \(\uparrow\) כאות הראשונה וכו '.
למקרה הכללי יותר של הוספה\(j_2\), \(j_1\) שייחשב בקרוב, נזמין את הקאטס באותה דרך "אלפביתית", ונכתוב תחילה את כל הקלפים שיש\(m_1=j_1\), וכן הלאה עד\(m_1=-j_1\):
\[ (j_1j_2,j_1(j_2-1),\dots ,j_1(-j_2), (j_1-1)j_2,(j_1-1)(j_2-1),\dots ,(j_1-1)(-j_2),\dots ,(-j_1)(-j_2)). \label{4.7.2}\]
הממדיות של מרחב זה היא אז. \((2j_1+1)\times (2j_2+1)\)
עכשיו בלוק הראשון של \(2j_2+1\) אלמנטים לכולם יש את אותו \(m\) מרכיב של\(j_1\), כלומר\(m_1=j_1\), את הבלוק הבא יש\(m_1=j_1-1\), וכן הלאה. חשבו מה המשמעות של זה לבניית מפעיל סיבוב הפועל על הכוסות במרחב הזה: אם הוא פועל רק על המומנטום הזוויתי\(j_1\), הוא ישנה את הגורמים \(m_1\) המכפילים את הבלוקים, אם המפעיל מסתובב בלבד\(j_2\), הוא יפעל בתוך כל בלוק, כל הבלוקים משתנים באותו אופן.
כדי לקבל תחושה כיצד זה עובד בפועל, אנו חוזרים למקרה הפשוט ביותר, שני סיבובים חצי.
המרחב הוא ארבע-ממדי, בעל בסיס\(|\uparrow_e\uparrow_p\rangle ,\; |\uparrow_e\downarrow_p\rangle ,\; |\downarrow_e\uparrow_p\rangle ,\; |\downarrow_e\downarrow_p\rangle\).
כל מפעיל הפועל על הספינים יוצג על ידי \(4\times 4\) מטריצה, שנחשב בצורה הטובה ביותר \(2\times 2\) כמטריצה המורכבת \(2\times 2\) מבלוקים: מפעיל הפועל על ספין הפרוטון פועל בתוך הבלוקים, אחד הפועל על ספין האלקטרונים משפיע על הגורמים המתרבים הכוללים מול כל בלוק.
בואו נסתכל על כמה דוגמאות. נזכיר כי מפעיל הגיוס לסיבוב יחיד הוא \(2\times 2\) המטריצה\(S^+=\hbar\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\). אז מהו מפעיל ההעלאה של ספין האלקטרונים?
\[ S^+_e\otimes I_p=\hbar\begin{pmatrix} 0&I \\ 0&0 \end{pmatrix}=\hbar\begin{pmatrix} 0&0&1&0 \\ 0&0&0&1 \\ 0&0&0&0 \\ 0&0&0&0 \end{pmatrix}. \label{4.7.3}\]
אנו משתמשים מודגש כדי לציין \(2\times 2\) מטריצות.
התבנית ברורה: המבנה הגדול (מודגש למעלה), זה של ארבעת \(2\times 2\) הבלוקים, משקף את המבנה של מפעיל ספין האלקטרונים\(S^+=\hbar\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\), בתוך אותם בלוקים (שרק אחד מהם שורד) מפעיל הזהות \(I=\begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix}\) פועל על ספין הפרוטון.
המפעיל שמעלה את ספין הפרוטון הוא: \[ I_e\otimes S^+_p=\hbar \begin{pmatrix} \sigma^+&0\\ 0&\sigma^+ \end{pmatrix}=\hbar \begin{pmatrix} 0&1&0&0\\ 0&0&0&0\\ 0&0&0&1\\ 0&0&0&0 \end{pmatrix}. \label{4.7.4}\]
מה לגבי המפעיל שמעלה גם ספין אלקטרונים וגם פרוטונים? במקרה זה, דפוס הבלוקים והתבנית בתוך כל בלוק חייבים להיות שניהם\(\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\), כך
\[ S^+_e\otimes S^+_p=\hbar^2\begin{pmatrix} 0&\sigma^+\\ 0&0 \end{pmatrix}=\hbar^2\begin{pmatrix} 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix}. \label{4.7.5}\]
יש רק אלמנט מטריצה אחד שאינו אפס מכיוון שרק חבר אחד בבסיס שורד פעולה זו.
אם שני ספינים מתקשרים (באמצעות הרגעים המגנטיים שלהם, למשל) באופן השומר על המומנטום הזוויתי הכולל, מונח אפשרי בהמילטוניאן יהיה \(S^-_eS^+_p\) מיוצג על ידי:
\[ S^-_eS^+_p=\hbar \begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&1&0&0\\ 0&0&0&0 \end{pmatrix}=\hbar S^-_e\otimes S^+_p. \label{4.7.6}\]
ייצוג מפעיל הסיבוב לשני ספינים
נזכיר מההרצאה על ספין שמפעיל הסיבוב בסיבוב יחיד הוא חצי \[ D^{(1/2)}(R(\theta \hat{\vec{n}}))=e^{\frac{-i\theta \hat{\vec{n}}\cdot\vec{J}}{\hbar}} =e^{-i(\theta /2)(\hat{\vec{n}}\cdot \vec{\sigma})}=I\cos\frac{\theta}{2}-i(\hat{\vec{n}}\cdot \vec{\sigma})\sin\frac{\theta}{2} \label{4.7.7}\]
\(2\times 2\)בסחרור או בחלל. כפי שקבענו, למפעיל המטריצה הזה יש את הטופס \[ \begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}= \begin{pmatrix} \cos(\theta /2)-in_z\sin(\theta /2)&-(in_x+n_y)\sin(\theta /2)\\ (-in_x+n_y)\sin(\theta /2)&\cos(\theta /2)+in_z\sin(\theta /2) \end{pmatrix}. \label{4.7.8}\]
עם\(|a|^2+|b|^2=1\).
מערכת \(2\times 2\) מטריצות יחידה זו מהווה ייצוג של קבוצת הסיבוב במובן זה שהסך הכל הנובע משני סיבובים רצופים ניתן על ידי המטריצה שהיא תוצר המטריצה של אלה התואמים לשני הסיבובים.
מהדיון בסעיף הקודם, צריך להיות ברור שבמרחב המוצר של שני הסיבובים, הייצוג של מפעיל הסיבוב - שני הספינים כמובן עוברים את אותו סיבוב - הוא:
\[ \begin{pmatrix} a\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}& b\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}\\ -b^*\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}& a^*\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix} \end{pmatrix} = \begin{pmatrix} a^2&ab&ab&b^2\\ -ab^*&aa^*&-bb^*&a^*b\\ -ab^*&-bb^*&aa^*&a^*b\\ b^{*2}&-a^*b^*&-a^*b^*&a^{*2} \end{pmatrix}. \label{4.7.9}\]
קבוצת \(4\times 4\) מטריצות זו, שוב עם\(|a|^2+|b|^2=1\), חייבת ליצור ייצוג של קבוצת הסיבוב על פני המרחב הארבע-ממדי. בקרוב נגלה שניתן לפשט ייצוג זה, אך כדי להשיג זאת עלינו לנתח את המצבים במונחים של המומנטום הזוויתי הכולל.
ייצוג מצבים של שני ספינים במונחים של מומנטום זוויתי כולל
כעת אנו מוכנים לבחון את מצבי הסיבוב הכוללים של אטום המימן של מצב הקרקע (אפס תנע זוויתי מסלול).
שקול תחילה את המצב כאשר ספין האלקטרונים והפרוטונים מצביעים כלפי מעלה,\(|\uparrow \uparrow \rangle\). המרכיב \(z\) - של הספין הכולל הוא\(S_z=S^e_z+S^p_z\), כך\(S_z=\hbar\). תיוג מצב הספין הכולל\(|s,m\rangle\), יש לנו מדינה עם\(m=1\), כך\(s=1\). (כדי לאשר כי אכן יש למצב זה \(s=1\) אנו יכולים להחיל את מפעיל גיוס הספין הכולל. \(S_+=S^e_+ +S^p_+\) מכיוון שלשני סיבובי הרכיבים יש \(m\) ערך מקסימלי,\(S_+|s,1\rangle_{sm}=(S^e_+ +S^p_+)|\uparrow \uparrow \rangle =0\), אך נותן אפס \(S_+\) רק כאשר הוא פועל על חבר m=s בכפולה.)
אנו מוצאים, אם כן, כי \(|\uparrow \uparrow \rangle =|1,1\rangle_{sm}\) במקום שבו הוספנו את הסיומת \(sm\) כדי להבהיר כי המספרים ב- ket האחרון מסמנים את \(|s,m\rangle\) הספין הכולל. לסיבוב הכולל\(s=1\), בהיותו מצב עצמי של מומנטום זוויתי כולל, יש שלישיית \(m\) ערכים\(m=1,0,-1\), \(|1,1\rangle_{sm}\) בהיותו החבר העליון. \(m=0\)החבר נמצא על ידי החלת מפעיל ההנמכה על\(|\uparrow \uparrow \rangle\):
\[ S_-|\uparrow \uparrow \rangle =(S^e_-+S^p_-)(|\uparrow \rangle_e\otimes |\uparrow \rangle_p)=\hbar |\downarrow \rangle_e\otimes |\uparrow \rangle_p+\hbar |\uparrow \rangle_e\otimes |\downarrow \rangle_p \label{4.7.10}\]
אשר יחד עם
\[ S_-|\uparrow \uparrow \rangle =S_-|1,1\rangle_{sm}=\sqrt{2}\hbar |1,0\rangle_{sm}, \label{4.7.11}\]
נותן
\[ |1,0\rangle_{sm}=\frac{1}{\sqrt{2}}(|\downarrow \uparrow \rangle +|\uparrow \downarrow \rangle ). \label{4.7.12}\]
ברור, החבר השלישי של השלישייה,. \(|1,-1\rangle_{sm}=|\downarrow \downarrow \rangle\)
אך שלישייה זו מהווה רק שלושה מצבי בסיס בייצוג המומנטום הזוויתי \(|s,m\rangle\) הכולל. מצב רביעי, אורתוגונלי לשלושת אלה ונורמל, הוא. \(\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\) זה\(m=0\), וגם בדק\(s=0\), בקלות על ידי ציון כי מפעיל הגיוס הפועל על מצב זה נותן אפס, כך שלמדינה יש את המקסימום המותר \(m\) \(s\) לערכו.
לסיכום: במומנטום הזוויתי הכולל |s, m\ ייצוג rangle לשני ספינים חצי, ארבעת מצבי הבסיס הם. \(|1,1\rangle_{sm},\; |1,0\rangle_{sm},\; |1,-1\rangle_{sm},\; |0,0\rangle_{sm}\) בסיס אורתונורמלי זה משתרע על אותו חלל כמו הסט האורתונורמלי האחר. \(|\uparrow \uparrow \rangle ,\; |\uparrow \downarrow \rangle ,\; |\downarrow \uparrow \rangle ,\; |\uparrow \uparrow \rangle\) בניית \(|s,m\rangle\) המדינות לעיל מסתכמת במציאת קבוצה אחת של נקודות בסיס מבחינת האחרות.
שים לב שמכיוון ששתי קבוצות הבסיס הן אורתונורמליות, מיפוי וקטור מקבוצה אחת לשנייה הוא טרנספורמציה יחידה. אבל יש עוד: המקדמים שמצאנו המבטאים בסיס אחד ket בבסיס השני הם כולם אמיתיים. המשמעות היא שאם לקט כלשהו יש מקדמים אמיתיים בבסיס אחד, הוא עושה זאת באחר. במקרה המיוחד הזה של כל המקדמים האמיתיים, טרנספורמציה יחידה מכונה אורתוגונלית.
קל לבנות את הטרנספורמציה האורתוגונלית המבטאת בסיס אחד במונחים של השני:
\[ \begin{pmatrix} |1,1\rangle_{sm}\\ |1,0\rangle_{sm}\\ |0,0\rangle_{sm}\\ |1,-1\rangle_{sm} \end{pmatrix}=\begin{pmatrix} 1&0&0&0\\ 0&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\ 0&\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0\\ 0&0&0&1 \end{pmatrix} \begin{pmatrix} |\uparrow \uparrow \rangle\\ |\uparrow \downarrow \rangle\\ |\downarrow \uparrow \rangle\\ |\downarrow \downarrow \rangle \end{pmatrix}. \label{4.7.13}\]
המטריצה היא אורתוגונלית וסימטרית, כך גם הפוך משלה.
מבחינה גיאומטרית, \(s=1\) פירושו שסיבובי הרכיבים מקבילים, שכן \(s=0\) הם אנטי מקבילים. זה יכול להיות מדויק יותר:\(2\vec{S}_1\cdot\vec{S}_2=S^2-S^2_1-S^2_2\), כך עבור \(s=1\)\(\vec{S}_1\cdot\vec{S}_2=\frac{1}{2}\hbar^2\left( 2-\frac{3}{4}-\frac{3}{4}\right)=\hbar^2/4\),, ועבור \(s=0\)\(\vec{S}_1\cdot\vec{S}_2=-\frac{3}{4}\hbar^2\). זה מקל על בניית מפעילי הקרנה לתוך \(s=0\) \(s=1\) מרחבי המשנה:\(P_{s=1}=(\vec{S}_1\cdot\vec{S}_2/\hbar^2)+\frac{3}{4}\).
דוגמה לפיזיקה: מקרה מעניין של מערכת דו-ספין הוא מולקולת המימן. סיבובי האלקטרונים נמצאים במצב סינגלט (אחרת המולקולה מתנתקת) אך שני סיבובי הפרוטונים, המקיימים אינטראקציה דרך המומנטים המגנטיים שלהם) יכולים להיות מקבילים (ספין כולל אחד), זה נקרא אורתוהידרוגן, או אנטי -מקביל (parahydrogen). הפרש האנרגיה קטן מספיק כדי שבטמפרטורת החדר היחס בין אורתו לפארה הוא 3:1, כלומר כל מצבי הספין סבירים באותה מידה (למעשה טמפרטורה אינסופית), אך בטמפרטורות נמוכות יותר שולטת צורת הפאר האנרגטית הנמוכה יותר. זה למעשה רלוונטי לטכנולוגיית אחסון מימן נוזלי: שיעור ההמרה מאורתו לפארה הוא איטי מאוד, אך כאשר הוא מתרחש אנרגיה משתחררת. אם זה קורה לאחר האחסון, נדרש קירור נוסף. כדי למנוע זאת, ניתן להשתמש בזרזים כדי לזרז את קצב ההמרה במהלך הקירור.
ייצוג מפעיל הסיבוב בבסיס המומנטום הזוויתי הכולל
כבר קבענו כי מפעיל הסיבוב, הפועל על מערכת שתי הספין, יכול להיות מיוצג על ידי \(4\times 4\) מטריצה, וכי ניתן להגיע לבסיס החדש (המומנטום הזוויתי הכולל) מהבסיס המקורי (שני ספין נפרד) על ידי הטרנספורמציה האורתוגונלית שניתנה במפורש לעיל. לכן, לפני ואחרי הכפלה של מפעיל סיבוב שני ספין למעשה ייתן ייצוג \(4\times 4\) מטריצה של מפעיל הסיבוב בבסיס המומנטום הזוויתי הכולל החדש.
עם זאת, גישה זו מפספסת את הנקודה: ראשית, למצב הסינגלט \(\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\) יש אפס תנע זוויתי, ולכן אינו משתנה על ידי סיבוב.
שנית, למצב השלישייה יש תנע זוויתי אחד, ולכן מפעילי סיבוב חייבים לפעול עליו בדיוק כפי שמצאנו קודם עבור מומנטום זוויתי: \[ D^{(1)}(R(\vec{\theta}))=e^{\frac{-i\theta \hat{\vec{n}}\cdot\vec{J}}{\hbar}} =I+(\cos\theta -1)\left( \frac{\hat{\vec{n}}\cdot\vec{J}}{\hbar} \right)^2-i\sin\theta \left( \frac{\hat{\vec{n}}\cdot\vec{J}}{\hbar} \right). \label{4.7.14}\]
המשמעות היא שמבחינת סיבובים, המרחב המשתרע על ידי ארבעת החבטים \(|0,0\rangle_{sm},\; |1,1\rangle_{sm},\; |1,0\rangle_{sm},\; |1,-1\rangle_{sm}\) הוא למעשה סכום של שני תת-מרחבים נפרדים, המרחב החד-ממדי והחלל \(|0,0\rangle_{sm}\) התלת מימדי שיש לו בסיס. \(|1,1\rangle_{sm},\; |1,0\rangle_{sm},\; |1,-1\rangle_{sm}\) תחת סיבוב, וקטור באחד ממרחבי המשנה הללו נשאר שם: אין מונחים צולבים במטריצה המערבבת את החללים.
המשמעות היא שלמטריצת הסיבוב יש את הצורה \(\begin{pmatrix} I&0\\ 0&R_3 \end{pmatrix}\) שבה \(R_3\) \(3\times 3\) המטריצה לסיבוב אחד, \(I\) היא רק המטריצה \(1\times 1\) הטריוויאלית בתת-מרחב הסינגלט, במילים אחרות 1, וה- \(0\)'s הם \(1\times 3\) \(3\times 1\) וקבוצות אפסים.
מצב של ספינים יכול כמובן להיות סכום של רכיבים בשני subspaces, למשל
\[ |\uparrow \downarrow \rangle =\frac{1}{\sqrt{2}}\left( \frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle +|\downarrow \uparrow \rangle )+\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\right). \label{4.7.15}\]
ייצוגים קבוצתיים ניתנים לצמצום ובלתי ניתנים לצמצום
התחלנו את הדיון שלנו בשני ספינים חצי אחד על ידי בחינת תכונות של מפעילי ספין במרחב התוצר הארבע-ממדי של מרחבי הסיבוב הדו-ממדיים, והמשכנו לבנות ייצוג ארבע-ממדי של מפעיל הסיבוב הכללי במרחב זה: ייצוג מטריצה של קבוצת הסיבוב. אך כאשר מערכת הדו-ספין מסומנת במונחים של תנע זוויתי כולל, אנו מגלים שלמעשה מפעיל הסיבוב הארבע-ממדי הזה הוא סכום של סיבוב תלת מימדי, וסיבוב זהות טריוויאלי למצב אפס תנע זוויתי. ניתן "לאלכסן" את האופרטור הארבע-ממדי: החלל מתפצל למרחב תלת מימדי ולמרחב חד ממדי שאינם מתערבבים תחת סיבוב, וכל מצב של המערכת הוא סכום של kets משני החללים.
זה בא לידי ביטוי לעתים קרובות באומרו כי שטח המוצר של שני ספינים חצי הוא סכום של ספין רווח אחד וספין אפס רווח, וכתוב \[ \frac{1}{2}\otimes \frac{1}{2}=1\oplus 0. \label{4.7.16}\]
לשים את הממדים של החללים במשוואה זו, \[ 2\times 2=3+1.\label{4.7.17}\]
בדיקה פשוטה זו על הממדיות הכוללת קובעת את התבנית עבור חללי מוצרים מסובכים יותר שנבדקו להלן.
\(4\times 4\)הייצוג של מפעיל הסיבוב אמור להיות ייצוג הניתן לצמצום: ניתן לצמצם אותו לסכום של ייצוגים ממדיים קטנים יותר. ייצוג בלתי ניתן לצמצום הוא כזה שבו אין תת-מרחבים בלתי משתנים תחת כל הסיבובים.
נזכיר שבנינו את \(4\times 4\) הייצוג הניתן לצמצום על ידי לקיחת תוצר ישיר של ייצוגי \(2\times 2\) הספין של חצי קבוצת הסיבוב. המשוואה בה \(\frac{1}{2}\otimes \frac{1}{2}=1\oplus 0\) השתמשנו לעיל לתיאור מרחבי הקט משמשת לעתים קרובות גם לתיאור ייצוגי קבוצת הסיבוב בתוך אותם תת-מרחבים.
אפשר לתהות מדוע היינו טורחים לבנות שני בסיסים שונים לאותו מרחב וקטורי. הסיבה היא שבעיות שונות זקוקות לבסיסים שונים. עבור מערכת של שני ספינים בשדה מגנטי חיצוני, שאינם מתקשרים זה עם זה, בסיס הספינים העצמאי וכו '\(|\uparrow \uparrow \rangle\), הוא טבעי. מצד שני, עבור אטום מימן ללא שדה חיצוני, אך כולל אינטראקציה בין הספינים (המיושרים לרגעי הדיפול המגנטיים של החלקיקים) \(|j,m\rangle\) הבסיס הוא הנכון: האינטראקציה המילטוניאן פרופורציונאלית\(\vec{S}^e\cdot\vec{S}^p\), שיכולה להיות כתוב\(\frac{1}{2}(S^e_x+iS^e_y)(S^p_x-iS^p_y)+\frac{1}{2}(S^e_x-iS^e_y)(S^p_x+iS^p_y)+S^e_zS^p_z\), שם אנו מזהים את מפעילי ההעלאה וההורדה של הספינים הבודדים. המשמעות היא שהמדינה\(|\uparrow \downarrow \rangle\), למשל, לא יכולה להיות מצב עצמי אם המילטוניאן כולל\(\vec{S}^e\cdot\vec{S}^p\), אך במקרה זה המדינות \(|j,m\rangle\) הן מצבים עצמיים מכיוון \(\vec{S}^e\cdot\vec{S}^p\) שנוסעים עם המומנטום הזוויתי הכולל ומרכיביו.
אבל מה יהיה בסיס טוב לאטום מימן, כולל \(\vec{S}^e\cdot\vec{S}^p\) המונח, ובשדה מגנטי חיצוני? זה תרגיל נחמד לקורא.
הוספת ספין למומנטום זוויתי מסלולי
בחלק זה, אנו רואים אטום מימן במצב עם תנע זוויתי מסלולי שאינו אפס,\(\vec{L}\neq0\). תנועה מסלולית כזו שקולה ללולאת זרם חשמלי ומייצרת שדה מגנטי. מומנט הדיפול המגנטי הקשור לסיבוב האלקטרונים מקיים אינטראקציה עם שדה זה, למילטוניאן המתאים יש מונח פרופורציונלי ל\(\vec{L}\cdot \vec{S}\), והוא מכונה אינטראקציה בין ספין-מסלול. לפרוטון יש גם רגע מגנטי, אבל זה קטן בשלושה סדרי גודל מזה של האלקטרון, אז נזניח אותו לעת עתה.
האינטראקציה בין \(\vec{L}\cdot \vec{S}\) ספין-מסלול מנותחת באופן הטבעי ביותר במצבי הבסיס של המומנטום הזוויתי הכולל,\(|j,m\rangle\), שם \(\vec{J}=\vec{L}+\vec{S}\) (ראה הדיון המקביל באינטראקציה של ספין-ספין לעיל). כתוב את מצבי המומנטום הזוויתי במסלול \(|l,m_l\rangle\) ואת מצבי הסיבוב \(|s,m_s\rangle\) היכן \(|\frac{1}{2},\frac{1}{2}\rangle =|\uparrow \rangle\) ו. \(|\frac{1}{2},-\frac{1}{2}\rangle =|\downarrow \rangle\) מרחב המוצר \(|l,m_l\rangle \otimes |s,m_s\rangle\) הוא \(2(2l+1)\) ממדי: ket יחיד במרחב המוצר הזה יתואר במלואו על ידי\(|l,m_l;s,m_s\rangle\), אך מכיוון ששניהם \(l,s\) קבועים לאורך כל הבעיה, המשתנים האמיתיים היחידים הם \(m_l,m_s\) כך שנכתוב את ה- ket בצורה הקומפקטית יותר\(|m_l,m_s\rangle_{m_lm_s}\), למשל\(|2,\frac{1}{2}\rangle_{m_lm_s}\).
מרכיב המומנטום הזוויתי המרבי האפשרי בכיוון z הוא בבירור\((l+\frac{1}{2})\hbar\), עבור המדינה\(|l,\frac{1}{2}\rangle_{m_1m_2}\). בייצוג המומנטום הזוויתי הכולל, זו חייבת להיות המדינה\(|j,m\rangle =|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}\). אז לשני הבסיסים השונים יש חבר משותף: \[ |l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}=|l,\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.18}\]
\(|j,m\rangle\)בייצוג המומנטום הזוויתי הכולל, \(|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}\) הוא \(m\) המצב העליון של ריבוי שיש \(2(l+\frac{1}{2})+1=2l+2\) בו חברים. בדיוק כמו במקרה של ספין ספין, החבר הבא למטה של multiplet נוצר על ידי החלת מפעיל ההורדה: \[ \begin{matrix} J_-|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}=\sqrt{2l+1} \hbar |l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\\ =(L_-+S_-)|l,\frac{1}{2}\rangle_{m_lm_s}\\ =\sqrt{2l} \hbar |l-1,\frac{1}{2}\rangle_{m_lm_s}+\hbar |l,-\frac{1}{2}\rangle_{m_lm_s} \end{matrix}. \label{4.7.19}\]
לכן \[ |l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}=\sqrt{\frac{2l}{2l+1}}|l-1,\frac{1}{2}\rangle_{m_lm_s}+\sqrt{\frac{1}{2l+1}}|l,-\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.20}\]
מצב זה \(|l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\) טמון \(m=l-\frac{1}{2}\) בתת-מרחב, שהוא דו מימדי, בעל וקטורי בסיס \(|l-1,\frac{1}{2}\rangle_{m_lm_s}\) \(|l,-\frac{1}{2}\rangle_{m_lm_s}\) ובייצוג. \(|\rangle_{m_lm_s}\) אז חייבים להיות לו שני וקטורי בסיס גם \(|\rangle_{jm}\) בייצוג. \(|\rangle_{jm}\)הקט השני חייב להיות אורתוגונלי \(|l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\) ומנורמל: זה יכול להיות רק \[ |l-\frac{1}{2},l-\frac{1}{2}\rangle_{jm}=\sqrt{\frac{2l}{2l+1}}|l,-\frac{1}{2}\rangle_{m_lm_s}-\sqrt{\frac{1}{2l+1}}|l-1,\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.21}\]
ייצגנו את ket החדש הזה \(|\rangle_{jm}\) כמצב העליון של \( j=l-\frac{1}{2}\) ריבוי. קל לבדוק שזה אכן המקרה: יש לו\(m=l-\frac{1}{2}\), \(J_+\) והפעולה עליו נותנת אפס, ולכן עליו להיות החבר העליון בריבוי שלו. העמימות היחידה היא שלב כולל: אמנת קונדון-שורטלי היא שלמצב m הגבוה ביותר של המומנטום הזוויתי של הרכיב הגדול יותר מוקצה מקדם חיובי.
\(|l-\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\)כך גם המצב העליון של ריבוי חדש שיש \(2(l-\frac{1}{2})+1=2l\) בו חברים. לשני המולטיפלטים \(j=l+\frac{1}{2}\) \(j=l-\frac{1}{2}\) ונלקחים יחד יש \(2(2l+1)\) חברים, ולכן הם משתרעים על כל המרחב \(2(2l+1)\) הממדי. שאר וקטורי \(|\rangle_{jm}\) הבסיס נוצרים על ידי יישום חוזר של מפעיל ההורדה בשני המולטיפלטים.
הסיבה שיש רק שני מולטיפלטים בבעיה זו היא שיש רק שתי דרכים שהסיבוב מחצית יכול להצביע ביחס למומנטום הזוויתי במסלול. כזכור כי עבור שני הסיבובים ביטאנו את מרחב המוצר סכום של רווח ספין 1 ומרחב ספין 0\(\frac{1}{2}\otimes \frac{1}{2}=1\oplus 0\), המשוואה האנלוגית כאן היא \[ \frac{1}{2}\otimes l=(l+\frac{1}{2})\oplus (l-\frac{1}{2}). \label{4.7.22}\]
במקרה הכללי של הוספת מומנטה זוויתית \(j_1, j_2\) עם\(j_1\ge j_2\), נוצרים \(2j_2+1\) מולטיפלטים, המתאימים למספר הכיוונים היחסיים האפשריים של שתי המומנטה הזוויתית.
הוספת שתי מומנטה זוויתית: המקרה הכללי
מרחב הקטים המתאר שתי מומנטות זוויתיות \(j_1, j_2\) הוא תוצר ישיר של שני חללים כל אחד למומנטום זוויתי יחיד, אך אופי המוצר הישיר של הקטים בדרך כלל אינו מפורש, \(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) ניתן לכתוב כקט \(|j_1,m_1;j_2,m_2\rangle\) יחיד. בדיוק כמו בדוגמאות לעיל, מכיוון \(j_1, j_2\) שהם קבועים לאורך כל הדרך, אין צורך לכתוב אותם בכל ket, פשוט נכתוב\(|m_1,m_2\rangle\), או, כאשר עוסקים בערכים מספריים, נוסיף \(m_1m_2\) כסיומת:. \(|2,3\rangle_{m_1m_2}\)
הכיסים \(|m_1,m_2\rangle\) מהווים בסיס אורתונורמלי שלם של מרחב התוצר \((2j_1+1)(2j_2+1)\) הממדי של שתי המומנטה הזוויתית: הם המצבים העצמיים של מערך המשתנים הנוסעים. \(\vec{J}_1^2,\; J_{1z},\; \vec{J}^2_2, \; J_{2z}\)
סך מדינות בסיס המומנטום הזוויתי
יש כמובן בסיס אורתוגונלי שלם חלופי של המרחב של שתי המומנטה הזוויתית: עבור המומנטום הזוויתי הכולל\(\vec{J}=\vec{J}_1+\vec{J}_2\), קבוצה שונה של משתני נסיעה שלמים היא:. \(\vec{J}_1^2,\; \vec{J}^2_2,\; \vec{J}^2,\; J_z\) (זו לא אותה קבוצה של מדינות כמו בפסקה הקודמת: לדוגמה, \(\vec{J}^2\) לא נוסע עם\(J_{1z}\). בדוק את זה!)
קבוצה חלופית זו מהווה בסיס טוב יותר לשתי מומנטות זוויתיות המקיימות אינטראקציה זו עם זו - מונח אינטראקציה כמו \(\vec{J}_1\cdot \vec{J}_2\) יכול להשתנות \(m_1, m_2\) אך לא\(m=m_1+m_2\), או. \(\vec{J}^2\)
כמו תמיד, אנו לוקחים \(\vec{J}_1^2,\; \vec{J}^2_2\) להיות קבועים לאורך כל הדרך, כך שהמשתנים המשמעותיים כאן הם \(\vec{J}^2\) ו\(J_z\), ואנחנו כותבים את המצבים פשוט כמו \(|j,m\rangle\) או כאשר יש לנו ערכים מספריים\(|3,1\rangle_{jm}\), בעקבות הסימון שהוצג לעיל. כמובן,\(\vec{J}^2|j,m \rangle =j(j+1)\hbar^2|j,m \rangle\), ו\(J_z|j,m \rangle =m\hbar |j,m \rangle\).
מעבר מבסיס אחד למשנהו: מקדמי קלבש-גורדן
איך כותבים מדינה \(|j,m\rangle\) במונחים של מדינות\(|m_1,m_2\rangle\)? יתר על כן, כיצד נוכיח שמערך המדינות החדש \(|j,m\rangle\) הוא בסיס שלם למרחב?
אנו יודעים שמערכת המצבים \(|m_1,m_2\rangle\) היא בסיס שלם, שכן החלל כולו הוא מרחב מוצר של \(j_1\) \(j_2\) וחללים, המשתרעים על ידי הסטים\(|m_1\rangle\), \(|m_2\rangle\) בהתאמה. לכן ניתן לכתוב את מפעיל הזהות \[ I=\sum_{m_1=-j_1}^{j_1}\sum_{m_2=-j_2}^{j_2}|m_1,m_2\rangle \langle m_1,m_2|. \label{4.7.23}\]
מכאן \(|j,m\rangle\) ניתן לבטא כסכום על וקטורי הבסיס\(|m_1,m_2\rangle\): \[ |j,m\rangle=\sum_{m_1=-j_1}^{j_1}\sum_{m_2=-j_2}^{j_2}|m_1,m_2\rangle \langle m_1,m_2|j,m\rangle \label{4.7.24}\]
המקדמים \(\langle m_1,m_2|j,m \rangle\) נקראים מקדמי Clebsch Gordan, לעתים קרובות כתובים מקדמי CG.
תכונה מיידית אחת של מקדמי CG היא \(\langle m_1,m_2|j,m \rangle =0\) אלא אם כן\(m=m_1+m_2\). זה נובע מזהות המפעיל \(J_z=J_{1z}+J_{2z}\) שנלקחה בין חזייה לקט מבסיסים שונים, \[ \langle m_1,m_2|J_z|j,m\rangle =\langle m_1,m_2|J_{1z}+J_{2z}|j,m\rangle \label{4.7.25}\]
ו \[ J_z|j,m\rangle =m\hbar |j,m\rangle ,\; \langle m_1,m_2|(J_{1z}+J_{2z})=\langle m_1,m_2|(m_1+m_2)\hbar , \label{4.7.26}\]
כך \[ (m-m_1-m_2)\langle m_1,m_2|j,m\rangle =0. \label{4.7.27}\]
אנו כבר יודעים שהערך המרבי של \(m_1\) הוא\(j_1\), ושל \(m_2\) הוא\(j_2\), כך שהערך המרבי של \(m\) הוא\(j_1+j_2\). לכן, הערך המרבי של\(j=j_1+j_2\), כי אם זה יכול ללכת גבוה יותר, יהיה גבוה יותר \(m\) איפשהו בחלל, סותר\(m=m_1+m_2\).
עבור הסט\(|m_1,m_2\rangle\), יש ket אחד בעל הערך המקסימלי הזה של m:\(|j_1,j_2\rangle_{m_1m_2}\). באותה מידה, במערך המצבים \(|j,m\rangle\) יש רק אחד עם ה-m המקסימלי:\(|j_1+j_2, j_1+j_2\rangle_{jm}\). לכן, שני kets אלה חייבים להיות זהים (הגדרת גורם השלב השרירותי שווה לאחד): \[ |j_1,j_2\rangle_{m_1m_2}=|j_1+j_2, j_1+j_2\rangle_{jm}. \label{4.7.28}\]
עכשיו \(|j_1+j_2, j_1+j_2\rangle_{jm}\) הוא ket העליון בריבוי שיש \(2(j_1+j_2)+1\) חברים.
החבר הבא למעלה של המרובה נוצר כבעבר על ידי החלת האופרטור המוריד על שני הייצוגים: \[ J_-|j_1+j_2, j_1+j_2\rangle_{jm}=(J_{1-}+J_{2-})|j_1, j_2\rangle_{m_1m_2} \label{4.7.29}\]
נותן \[ \sqrt{2(j_1+j_2)}\hbar |j_1+j_2, j_1+j_2-1\rangle_{jm}=\sqrt{2j_1}\hbar |j_1-1, j_2\rangle_{m_1m_2}+\sqrt{2j_2}\hbar |j_1, j_2-1\rangle_{m_1m_2} \label{4.7.30}\]
כך \[ |j_1+j_2, j_1+j_2-1\rangle_{jm}=\sqrt{\frac{j_1}{j_1+j_2}}|j_1-1, j_2\rangle_{m_1m_2}+\sqrt{\frac{j_2}{j_1+j_2}}|j_1, j_2-1\rangle_{m_1m_2} \label{4.7.31}\]
ובאנלוגיה מדויקת למקרה מסלול הסיבוב, מצב \(|\rangle_{jm}\) הבסיס האחר \(m=j_1+j_2-1\) בתת-חלל הוא \[ |j_1+j_2-1, j_1+j_2-1\rangle_{jm}=-\sqrt{\frac{j_2}{j_1+j_2}}|j_1-1, j_2\rangle_{m_1m_2}+\sqrt{\frac{j_1}{j_1+j_2}}|j_1, j_2-1\rangle_{m_1m_2} \label{4.7.32}\]
עם אמנת הסימנים המתאימה ל\(j_1>j_2\). זהו החבר העליון של ריבוי שיש\(j=j_1+j_2-1\), וכך \(2(j_1+j_2-1)+1=2(j_1+j_2)-1\) חברים (נבדק כרגיל על ידי הגשת בקשה \(J_+\) וקבלת אפס).
כדי להמשיך הלאה, מפעיל ההורדה מוחל פעם נוספת, כדי להיכנס \(m=j_1+j_2-2\) למרחב המשנה. \(|\rangle_{m_1m_2}\)בייצוג, יש לזה שלושה וקטורי בסיס עצמאיים (מסופקים\(j_2>\frac{1}{2}\)):\(|j_1-2, j_2\rangle_{m_1m_2},\; |j_1-1, j_2-1\rangle_{m_1m_2},\; |j_1, j_2-2\rangle_{m_1m_2}\). אבל רק שני קטטים הורדו \(|\rangle_{jm}\) בייצוג - החלק השלישי החסר \(|\rangle_{jm}\) \(m=j_1+j_2-2\) בתת-חלל חייב להיות החבר העליון של ריבוי חדש אחר שיש לו\(j=j_1+j_2-2\), וכך חברים. \(2(j_1+j_2)-3\)
שים לב שהמקדמים שנוצרו על ידי המפעילים המורידים הם כולם אמיתיים, כך שניתן לכתוב את כל שלושת \(|\rangle_{jm}\) הקטים \(m=j_1+j_2-2\) בתת-חלל במונחים של \(|\rangle_{m_1m_2}\) הקטים עם מקדמים אמיתיים.
ניתן לחזור על תהליך זה עד \(|\rangle_{jm}\) שהמולטיפלטים שנוצרו יפרשו על החלל. נזכיר כי ממדיות המרחב, \(|\rangle_{m_1m_2}\) מהייצוג, היא. \((2j_1+1)(2j_2+1)\) המולטיפלטים \(|\rangle_{jm}\) מוסיפים למימדיות כוללת \[ 2(j_1+j_2)+1+2(j_1+j_2)-1+2(j_1+j_2)-3+\dots \label{4.7.33}\]
אבל איפה אנחנו עוצרים? השכל הישר מציע כי עבור\(j_1>j_2\), המומנטום הזוויתי הכולל המינימלי חייב להיות\(j=j_1-j_2\). אין בהכרח לסמוך על השכל הישר, אך ברור כי כל חברי המולטיפלטים \(|\rangle_{jm}\) שנוצרו על ידי שימוש באופרטור ההורדה, ואחריו הצגת חבר עליון מרובה-אורתוגונלי חדש בכל פעם, כמתואר לעיל, הם קטטים אורתונורמליים עצמאיים, ואם נעצור ב, המספר הכולל שנוצר הוא \(j=j_1-j_2\) \[ \sum_{n=|j_1-j_2|}^{j_1+j_2} (2n+1)=(2j_1+1)(2j_2+1). \label{4.7.34}\]
(השתמש\(\sum_{n=0}^{m}(2n+1)=(m+1)^2\).) זה קובע כי הכללת כל המומנטה הזוויתית הכוללת בין \(|j_1-j_2|\) לבין \(j_1+j_2\) אכן נותנת בסיס מלא המשתרע על החלל, כך
\[ j_1\otimes j_2=(j_1+j_2)\oplus (j_1+j_2-1)\oplus \dots \oplus (|j_1-j_2|). \label{4.7.35}\]
חישוב מקדמי קלבש-גורדן באמצעות יחסי רקורסיה
התוכנית שהוצגה לעיל, בניית רצף של מולטיפלטים המתחילים ממצב m הגבוה ביותר ושימוש באמנת קונדון-שורטלי ליישוב שלטים, תייצר את כל מקדמי ה- CG. עם זאת, גישה אחרת מוכיחה שימושית בעבודה מאוחרת יותר. נזכיר כי על ידי מציאת אלמנטים מטריקס של \(J_z=J_{1z}+J_{2z}\) בין \(\langle m_1,m_2|\) חזייה \(|j,m\rangle\) לקט, קבענו כי מקדמי Clebsch-Gordan הם אפס אלא אם כן. \(m=m_1+m_2\) הערכה מקבילה של מרכיבי המטריצה של \(J_{\pm} =J_{1\pm} +J_{2\pm}\) מניבה קשר בין שלושה מקדמי CG: \[ \langle m_1,m_2|J_+|j,m\rangle =\langle m_1,m_2|J_{1+}|j,m\rangle +\langle m_1,m_2|J_{2+}|j,m\rangle \label{4.7.36}\]
תשואות \[ \begin{matrix} \sqrt{j(j+1)-m(m+1)}\langle m_1,m_2|j,m+1\rangle =\\ \sqrt{j_1(j_1+1)-m_1(m_1-1)} \langle m_1-1,m_2|j,m\rangle +\sqrt{j_2(j_2+1)-m_2(m_2-1)}\langle m_1,m_2-1|j,m\rangle \end{matrix} \label{4.7.37}\]
כאשר \(J_{1+}\) משחק שמאלה מפחית \(m_1\) באחד. (כאן, כמובן, עלינו \(m=m_1+m_2-1\) לבחור שיהיו מקדמים שאינם אפסיים.)
כדי לדמיין מה קורה עם כל המקדמים האלה, זכור \(m_1\) יכול לקחת \(2j_1+1\) ערכים \(m_2\) ויכול לקחת \(2j_2+1\) ערכים, כך שבהתחשב \(j_1,j_2\) בכל מצב אפשרי של שני הספינים יכול להיות מיוצג על ידי נקודה \((2j_1+1)\times (2j_2+1)\) ברשת: הנה\(j_1=3, j_2=2\):
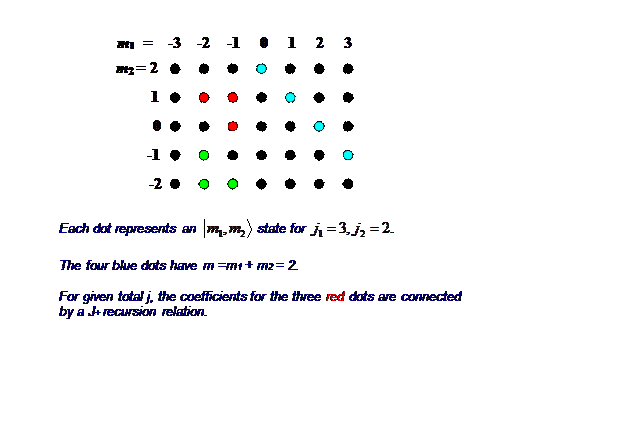
כיצד נקודות אלה קשורות למקדמי CG? הנקודה הימנית העליונה (3, 2) מייצגת באופן ייחודי את \(j=5,\; m=5\) מצב המומנטום הזוויתי הכולל. הנקודות הבאות למטה, (2, 2) ו- (3, 1), מתאימות לשני מקדמי CG עבור \(j=5\) ושני מקדמי CG שונים עבור. \(j=4\)
אם נבחר כעת ערך אחד של \(j\) פחות מ- \(j_1+j_2\), כל נקודה ברשת תתאים למקדם אחד.
שים לב כי לאחר תיקון\(j\), הרשת תהיה מקוצצת: בואו ניקח\(j=3\), כך \(m=m_1+m_2=3\) לכל היותר. ואז הרשת מאבדת את פינותיה הרחוקות: \[ |j_1,m_1\rangle \otimes |j_2,m_2\rangle. \label{4.7.38}\]
הבה נבחן עבור קבוע זה \(j\) אילו מקדמי CG נמצאים היכן ברשת מקוצצת זו.
יש בסך הכל \(2j+1=7\) מדינות עבור\(m=3, 2 ,\dots ,-3\).
המצב העליון,, או \(j=3,\; m=3\)\(|3,3\rangle_{jm}\), ניתן על ידי שלושה מקדמים בקו האלכסוני העליון (הוא נמצא בתת-מרחב תלת מימדי, ואורתוגונלי לחברים \(j=5\) \(j=4\) ומרובים\(|5,3\rangle_{jm}\), \(|4,3\rangle_{jm}\) שנמצאים גם הם בתת-מרחב). \(m=3\) אנחנו לא בשלב זה מחשבים את המקדמים האלה, אנחנו רק מנסים למצוא להם בית.
החלת האופרטור המוריד כדי לתת \(|3,3\rangle_{jm}\) וקטור \(m=2\) בתת-המרחב הארבע-ממדי, המקדמים יהיו שייכים לאלכסון הבא למטה, שיש בו ארבעה אלמנטים. (תת-מרחב זה כולל גם את החבר העליון של \(j=2\) המרובה.) באמצעות מפעיל ההנמכה פעם נוספת אנו נכנסים \(m=1\) לתת-המרחב החמש ממדי - אך זהו המספר המרבי של הממדים בבעיה זו, מכיוון שלא ניתן להוסיף מומנטה זוויתית 3 ו -2 כדי לתת סקלר. \(j=0\)
לאחר שכעת, עבור הספציפי הזה \(j\) שעשוי ממנו\(j_1+j_2\), נמצא היכן נמצאים כל מקדמי ה- CG עבור כל \(2j+1\) חברי המרובה, נראה כיצד ניתן לחשב את כולם באופן שיטתי באמצעות יחסי הרקורסיה שנוצרו על ידי. \(J_{\pm} =J_{1\pm} +J_{2\pm}\)
מיפינו את יחסי הרקורסיה בתרשים: בהתחשב \(j,\; j_1,\; j_2\) בשלוש הנקודות האדומות ב \((m_1,m_2),\; (m_1-1,m_2),\; (m_1,m_2-1)\) (עם \(m_1=-1,\; m_2=1\) בדוגמה זו) אתר את שלושת מקדמי ה- CG המספקים את המשוואה הליניארית למעלה מ \[ \langle m_1,m_2|J_+|j,m\rangle =\langle m_1,m_2|J_{1+}|j,m\rangle +\langle m_1,m_2|J_{2+}|j,m\rangle \label{4.7.39}\]
כך שאם שניים מהם ידועים השלישי ניתן. באופן דומה, המשוואה המקבילה שנוצרת על ידי \(J_-=J_{1-}+J_{2-}\) מקשרת בין שלוש הנקודות הירוקות, ב\((m_1,m_2),\; (m_1+1,m_2),\; (m_1,m_2+1)\).
אנו מתחילים בחישוב מקדמי ה- CG עם הנקודה הכחולה, הנקודה בקצוות ה"חץ "המובילים. תן לנו להקצות באופן שרירותי ערך 1 לנקודה זו. אם נהפוך אותו לחבר העליון במשולש "ירוק", זה יקשר אותו לנקודה למטה ולנקודה מימין שנמצאת מחוץ למערך. הנקודה מחוץ למערך תורמת אפס, כך שיש לנו משוואה שנותנת את ערך המקדם בנקודה שמתחת לנקודה הכחולה כמכפיל של הערך בנקודה הכחולה. לאחר מכן נוכל להמשיך עד לנקודה הבאה. במקום זאת יכולנו לעלות מהנקודה הכחולה באמצעות משולשים אדומים לא שלמים - למעשה אנו יכולים להמשיך סביב קצה המערך כולו. לאחר מכן, ברגע שהערכים לאורך הקצוות קבועים, ניתן להשתמש במשולשי הרקורסיה כדי לנוע פנימה ולמצוא את השאר.
הנקודה של סעיף זה היא לקבוע כי מלבד קבוע כפל כולל שיש לתקן על ידי נורמליזציה, \(j\) ניתן למצוא את כל מקדמי ה- CG לערך זה של מיחסי הרקורסיה בלבד. הסיבה שזה חשוב היא מכיוון שאותו מבנה אלגברי, ולכן אותם יחסי רקורסיה, משמשים להגדרת טנזורים כדוריים, כך שניתן לשלב אותם גם באמצעות אותם מקדמי CG. (אנו עדיין זקוקים לאמנת שלטים כאן כדי להציג טבלה שלמה: עד כה לערכים השונים של סך הכל \(j\) יש שלבים יחסיים שרירותיים.)


