4.6: אטום המימן

פקטורינג את מרכז התנועה ההמונית

אטום המימן מורכב משני חלקיקים, הפרוטון והאלקטרון, המקיימים אינטראקציה באמצעות פוטנציאל קולומב\(V(\vec{r_1}-\vec{r_2})=e^2/r\), שם כרגיל. \(r=|\vec{r_1}-\vec{r_2}|\) כתיבת ההמונים של שני החלקיקים כמשוואת \(m_1, m_2\) שרדינגר לאטום היא: \[ \left( -\frac{\hbar^2}{2m_1}\vec{\nabla_1}^2-\frac{\hbar^2}{2m_2}\vec{\nabla_2}^2-\frac{e^2}{r}\right) \psi(\vec{r_1},\vec{r_2})=E\psi(\vec{r_1},\vec{r_2}). \label{4.6.1}\]

אך \(\vec{r_1},  \vec{r_2}\) אינם משתני המיקום הטבעיים ביותר לתיאור מערכת זו: מכיוון שהפוטנציאל תלוי רק במיקום היחסי, בחירה טובה יותר \(\vec{r}, \vec{R}\) מוגדרת על ידי: \[ \vec{r}=\vec{r_1}-\vec{r_2},\;\; \vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2} \label{4.6.2}\]

כך \(\vec{R}\) הוא מרכז המסה של המערכת. זה נוח בעת ובעונה אחת כדי לציין את המסה הכוללת על ידי\(M=m_1+m_2\), ואת המסה מופחתת על ידי\(m=\frac{m_1m_2}{m_1+m_2}\).

טרנספורמציה בצורה פשוטה למשתנים שהמשוואה של \(\vec{r},  \vec{R}\) שרדינגר הופכת להיות \[ \left(-\frac{\hbar^2}{2M}\vec{\nabla_R}^2-\frac{\hbar^2}{2m}\vec{\nabla_r}^2-\frac{e^2}{r}\right)\psi(\vec{R}, \vec{r})=E\psi(\vec{R}, \vec{r}). \label{4.6.3}\]

כתיבת פונקציית הגל \[ \psi(\vec{R}, \vec{r})=\Psi(\vec{R})\psi(\vec{r}) \label{4.6.4}\]

אנחנו יכולים לפצל את המשוואה לשניים: \[ \begin{matrix} \left( -\frac{\hbar^2}{2M}\vec{\nabla_R}^2\right) \Psi(\vec{R})=E_R\Psi(\vec{R}) \\ \left( -\frac{\hbar^2}{2m}\vec{\nabla_r}^2+V(\vec{r})\right) \psi(\vec{r})=Er\psi(\vec{r}) \end{matrix}\label{4.6.5}\]

והאנרגיה הכוללת של המערכת היא\(E=E_R+E_r\). שימו לב שהתנועה של מרכז המסה היא (כמובן) בדיוק זו של חלקיק חופשי, בעל פתרון גל מישורי טריוויאלי. מעתה ואילך, נעסוק רק בתנועה היחסית של החלקיקים. מכיוון שהפרוטון כבד בהרבה מהאלקטרון, כמעט תמיד נתעלם מההבדל בין מסת האלקטרונים למסה המופחתת, אך יש לציין כי ההבדל ניתן לזיהוי בקלות בספקטרוסקופיה: למשל, הקווים משתנים אם הפרוטון מוחלף על ידי דאוטרון (מימן כבד).

אנו מוכנים לכתוב את משוואת שרדינגר לאטום המימן, להפיל את הסיומות r במשוואה השנייה למעלה ולכתוב במפורש בקואורדינטות כדוריות: \(\vec{\nabla}^2\)

\[ \begin{matrix} -\frac{\hbar^2}{2m}\left( \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2\frac{\partial\psi}{\partial r}\right) +\frac{1}{r^2 \sin\theta}\frac{\partial}{\partial\theta}\left( \sin\theta\frac{\partial\psi}{\partial\theta}\right) +\frac{1}{r^2\sin^2\theta}\frac{\partial^2\psi}{\partial\varphi^2}\right) -\frac{e^2}{r}\psi \\ =E\psi. \end{matrix} \label{4.6.6}\]

פקטורינג התלות הזוויתית: המשוואה הרדיאלית - \(R(r)\)

מכיוון שהפוטנציאל הוא סימטרי כדורית, המילטוניאן \(H\) נוסע עם מפעילי המומנטום הזוויתי\(L^2\), \(L_z\) כך שנוכל לבנות קבוצה משותפת של גלגלים עצמיים של שלושת המפעילים,,. \(H\) \(L^2\) \(L_z\) התלות הזוויתית של העצמיות הללו היא אפוא של ה- \(Y^m_l\)'s, ולכן הפתרונות חייבים להיות בצורה

\[ \psi_{Elm}(r,\theta,\phi)=R_{Elm}(r)Y^m_l(\theta,\phi). \label{4.6.7}\]

כעת, שימו לב שבמשוואת שרדינגר לעיל, החלק הזוויתי של \(\vec{\nabla}^2\) הוא בדיוק המפעיל הדיפרנציאלי\(L^2/2mr^2\), כך שפעולה עליו \(\psi_{Elm}(r,\theta,\phi)=R_{Elm}(r)Y^m_l(\theta,\phi)\) תיתן. \(\hbar^2l(l+1)/2mr^2\) לאחר מכן \(Y^m_l\) ניתן לבטל את ההרמוניה הכדורית משני צידי המשוואה ולהשאיר:

\[ \begin{matrix} -\dfrac{\hbar^2}{2m}\left( \dfrac{1}{r^2}\dfrac{d}{dr}(r^2\dfrac{d}{dr})-\dfrac{l(l+1)}{r^2}\right) R_{El}(r)-\dfrac{e^2}{r}R_{El}(r) \\ =ER_{El}(r) \end{matrix} \label{4.6.8}\]

עכשיו זה ברור כי \(R(r)\) לא יכול לסמוך על\(m\).

הנגזרות הרדיאליות מפשטות אם גורמים החוצה \(1/r\) מהפונקציה\(R\), כתיבה

\[ R_{El}(r)=\dfrac{u(r)}{r} \label{4.6.9}\]

ודיכוי זמני של \(E\) \(l\) וכדי להפחית את העומס.

המשוואה הופכת ל:

\[ -\dfrac{\hbar^2}{2m}\left( \dfrac{d^2}{dr^2}-\dfrac{l(l+1)}{r^2}\right) u(r)-\dfrac{e^2}{r}u(r)=Eu(r). \label{4.6.10}\]

סידור מחדש,

\[ -\dfrac{\hbar^2}{2m}\dfrac{d^2u(r)}{dr^2}+\left( \dfrac{\hbar^2}{2m}\dfrac{l(l+1)}{r^2}-\dfrac{e^2}{r}\right) u(r)=Eu(r). \label{4.6.11A}\]

שים לב שזה זהה למשוואת שרדינגר עבור חלקיק בממד אחד, מוגבל ל\(r>0\), בפוטנציאל (עבור\(l\neq 0\)) ללכת לאינסוף חיובי במקור, ואז שלילי והולך לאפס במרחקים גדולים, כך שתמיד יש לו מינימום עבור כמה חיובי. \(r\)

אנו מעוניינים במצבים קשורים של מערכת הפרוטון-אלקטרונים, כך \(E\) שתהיה כמות שלילית. בהפרדות גדולות, משוואת הגלים מפשטת

\[ -\dfrac{\hbar^2}{2m}\dfrac{d^2u(r)}{dr^2}\cong E u(r) (for\; large\; r) \label{4.6.11B}\]

שיש פתרונות משוערים\(e^{\kappa r}\), \(e^{-\kappa r}\) איפה\(\kappa =\sqrt{-2mE/\hbar^2}\). למצבים המאוגדים שאנו מחפשים, כמובן, יש פונקציות גל הפוחתות באופן אקספוננציאלי במרחקים גדולים.

הולך למשתנה חסר ממדים

כדי לפשט עוד יותר את המשוואה, אנו מציגים את המשתנה חסר הממדים \[ \rho=\kappa r,\;\; \kappa =\sqrt{-2mE/\hbar^2} \label{4.6.12}\]

נותן \[ \frac{d^2u(\rho)}{d\rho^2}=\left( 1-\frac{2\nu}{\rho}+\frac{l(l+1)}{\rho^2}\right) u(\rho) \label{4.6.13}\]

שם (מסיבות שיתבררו בקרוב) הצגנו \(\nu\) שהוגדרו על ידי \[ 2\nu=e^2\kappa /E. \label{4.6.14}\]

שימו לב שבטרנספורמציה \(r\) למשתנה \(\rho\) חסר הממדים גורם קנה המידה \(\kappa\) תלוי באנרגיה, כך שיהיה שונה עבור מצבים שונים הקשורים לאנרגיה!

שקול עכשיו את ההתנהגות של פונקציית הגל ליד המקור. המונח הדומיננטי לקטן מספיק \(\rho\) הוא המונח הצנטריפוגלי, כך \[ \frac{d^2u(\rho)}{d\rho^2}\cong \frac{l(l+1)}{\rho^2}u(\rho) \label{4.6.15}\]

שעבורם הפתרונות הם\(u(\rho)\sim \rho^{-l}\),\(u(\rho)\sim \rho^{l+1}\). מכיוון שפונקציית הגל אינה יכולה להיות יחידה, אנו בוחרים בשנייה.

קבענו שתפקוד הגל מתפורר כמו \(e^{-\kappa r}=e^{-\rho}\) במרחקים גדולים, \(\rho^{l+1}\) ומתקרב למקור. פקטורינג את שתי ההתנהגויות האסימפטוטיות הללו, מוגדר על ידי \(w(\rho)\) \[ u(\rho)=e^{-\rho}\rho^{l+1}w(\rho). \label{4.6.16}\]

זה פשוט (אם מייגע) לקבוע כי \(w(\rho)\) עונה על המשוואה הדיפרנציאלית: \[ \rho\frac{d^2w(\rho)}{d\rho^2}+2(l+1-\rho)\frac{dw(\rho)}{d\rho}+2(\nu-(l+1))w(\rho)=0. \label{4.6.17}\]

הכנסת פתרון סדרת ניסוי \( w(\rho)=\sum_{k=0}^{\infty}w_k\rho^k\) נותנת יחס הישנות בין מקדמים עוקבים: \[ \frac{w_{k+1}}{w_k}=\frac{2(k+l+1-\nu)}{(k+1)(k+2(l+1))}. \label{4.6.18}\]

עבור ערכים גדולים של \(k\)\(w_{k+1}/w_k\to 2/k\),, כך \(w_k\sim 2^k/k!\) ולכן\(w(\rho)\sim e^2\rho\). המשמעות היא שמצאנו את פונקציית הגל הרדיאלית המתפצלת\(u(\rho)\sim e^{\rho}\), שהיא למעשה ההתנהגות הנכונה לערכים כלליים של האנרגיה.

כדי למצוא את המצבים הכבולים, עלינו לבחור אנרגיות כך שהסדרה אינה אינסופית. כל עוד הסדרה נעצרת איפשהו, הירידה האקספוננציאלית תשתלט בסופו של דבר ותניב פונקציית גל סופית (מצב כבול). בדיוק כמו מתנד הרמוני פשוט, זה יכול לקרות רק אם עבור חלק\(k, w_{k+1}=0\). בדיקת היחס\(w_{k+1}/w_k\), ככל הנראה התנאי למצב כבול הוא זה \[ \nu=n,\;\; an\; integer \label{4.6.19}\]

ובמקרה זה הסדרה עבור \(w(\rho)\) מסתיימת ב\(k=n-l-1\). מעתה והלאה, מכיוון שאנו יודעים כי עבור הפונקציות שאנו מעוניינים בהן \(\nu\) הוא מספר שלם, אנו מחליפים \(\nu\) על ידי\(n\).

כדי למצוא את האנרגיות של מצבים קשורים אלה\(\kappa =\sqrt{-2mE/\hbar^2}\), זכור \(2n=2\nu=e^2\kappa /E\) וכך \[ 4n^2=\frac{e^4\kappa_n^2}{E_n^2}=-\frac{e^4}{E_n^2}\frac{2mE_n}{\hbar^2}, \label{4.6.20}\]

כך \[ E_n=-\frac{me^4}{2\hbar^2}\frac{1}{n^2}=-\frac{13.6}{n^2} ev = -\frac{1}{n^2} Rydberg. \label{4.6.21}\]

(זה מגדיר את רידברג, יחידת אנרגיה פופולרית בפיזיקה האטומית.)

למרבה הפלא, זוהי אותה סדרה של אנרגיות מצב כבולות שמצא בוהר מהמודל שלו! כמובן שעדיף שזה יהיה המקרה, מכיוון שסדרת האנרגיות שבוהר מצא היוו נכון את קווי הספקטרום הנפלטים מאטומי מימן חמים. עם זאת, שימו לב שיש כמה הבדלים חשובים במודל בוהר: האנרגיה כאן נקבעת כולה על ידי\(n\), המכונה המספר הקוונטי העיקרי, אך בניגוד למודל של בוהר, \(n\) אינה המומנטום הזוויתי. למצב הקרקע האמיתי של אטום המימן,\(n=1\), יש אפס תנע זוויתי: שכן\(n=k+l+1\), \(n=1\) פירושו שניהם \(l=0\) ו\(k=0\). פונקציית גל מצב הקרקע היא אפוא סימטרית כדורית, והתפקוד \(w(\rho)=w_0\) הוא רק קבוע. מכאן \(u(\rho)=\rho e^{-\rho}w_0\) ופונקציית הגל הרדיאלי בפועל היא זו מחולקת על ידי\(r\), וכמובן מנורמלת כראוי.

כדי לכתוב את פונקציית הגל במונחים של\(r\), אנחנו צריכים למצוא\(\kappa\). להרכיב\(\rho=\kappa_n r\), \(\kappa_n=\sqrt{-2mE_n/\hbar^2}\) ו\(E_n=-\frac{me^4}{2\hbar^2}\frac{1}{n^2}\), \[ \kappa_n=\sqrt{2m\frac{me^4}{2\hbar^2}\frac{1}{n^2}}/\hbar=\frac{me^2}{\hbar^2n}=\frac{1}{a_0n}, \label{4.6.22}\]

איפה האורך \[ a_0=\frac{\hbar^2}{me^2}=0.529\times 10^{-10}m. \label{4.6.23}\]

נקרא רדיוס בוהר: זהו למעשה רדיוס המסלול הנמוך ביותר במודל של בוהר.

תרגיל: בדוק הצהרה אחרונה זו.

ראוי לציין בשלב זה שניתן לכתוב את רמות האנרגיה במונחים של רדיוס \(a_0\) בוהר: \[ E_n=-\frac{e^2}{2a_0}\frac{1}{n^2}. \label{4.6.24}\]

(זה למעשה ברור: זכרו שהאנרגיות \(E_n\) זהות לאלו במודל בוהר, בו רדיוס \(n^{th}\) המסלול נמצא\(n^2a_0\), כך שהאנרגיה הפוטנציאלית האלקטרוסטטית היא \(-e^2/na_0\) וכו ').

עוברים למצבים הנרגשים: שכן\(n=2\), יש לנו ברירה: או שלפונקציה הרדיאלית \(w(\rho)\) יכול להיות מונח אחד, כמו קודם, אבל עכשיו המומנטום הזוויתי \(l=1\) (מאז\(n=k+l+1\)); או \(w(\rho)\) שיכולים להיות שני מונחים (כך\(k=1\)), ו\(l=0\). שתי האפשרויות נותנות את אותה אנרגיה, -0.25 Ry, מכיוון ש - n זהה, והאנרגיה תלויה \(n\) רק ב. למעשה, ישנם ארבעה מצבים באנרגיה זו, שכן \(l=1\) יש מצבים עם \(m=1, m=0\) ו\(m=-1\), ויש \(l=0\) לו את המצב האחד\(m=0\). (כרגע, אנחנו לא סופרים את הגורם הנוסף של 2 משני כיווני הספין האפשריים של האלקטרון.)

שכן\(n=3\), יש 9 מצבים בסך הכל: נותן אחד, \(l=1\) נותן 3 \(l=2\) ונותן 5 \(m\) ערכים שונים. למעשה, עבור המספר הקוונטי העיקרי \(n\) ישנם מצבים \(n^2\) מנווונים. (\(n^2\)בהיותם סכום המספרים השלמים \(n\) המוזרים הראשונים.)

ניתן למפות את המצבים, אנרגיה אנכית, מומנטום זוויתי אופקית:

האנרגיה\(E=-1/n^2\), הרמות מסומנות\(nl\), \(n\) בהיותה המספר הקוונטי העיקרי והסימון המסורתי למומנטום \(l\) זוויתי ניתן בתחתית התרשים. שני החצים האנכיים האדומים הם שני המעברים הראשונים בסדרת באלמר הספקטרוסקופית, שארבע שורות מהן נתנו לבוהר את הרמז שהוביל למודל שלו. הסדרה המקבילה של מעברים למצב \(1s\) הקרקע הם אולטרה סגול, הם נקראים סדרת Lyman.

פונקציות גל עבור כמה מדינות נמוכות

מעתה ואילך, אנו מתייגים את פונקציות הגל במספרים הקוונטיים\(\psi_{nlm}(r,\theta,\phi)\), כך שמצב הקרקע הוא הסימטרי הכדורי. \(\psi_{100}(r)\)

עבור מצב זה\(R(r)=u(r)/r\), שבו\(u(\rho)=e^{-\rho}\rho^{l+1}w(\rho)=e^{-\rho}\rho w_0\), \(w_0\) עם קבוע, ו\(\rho=\kappa_1 r=r/a_0\).

אז, כפונקציה של\(r\), \(\psi_{100}(r)=Ne^{-r/a_0}\) \(N\) עם קבוע נורמליזציה מוערך בקלות:

\[ \psi_{100}(r)=\left( \frac{1}{\pi a^3_0}\right)^{1/2}e^{-r/a_0}. \label{4.6.25}\]

שכן \(n=2, l=1\) הפונקציה \(w(\rho)\) היא עדיין מונח יחיד, קבוע, אבל עכשיו\(u(\rho)=e^{-\rho}\rho^{l+1}w(\rho)=e^{-\rho}\rho^2w_0\), ובשביל \(n=2\)\(\rho=\kappa r=r/2a_0\), לזכור את התלות האנרגטית של\(\kappa\).

לכן\(\psi_{210}(r,\theta,\phi)=N\left( \frac{r}{a_0}\right) e^{-r/2a_0}\cos\theta\). שוב, הערכת קבוע הנורמליזציה היא שגרתית ומניבה \[ \psi_{210}(r,\theta,\phi)=\left( \frac{1}{32\pi a^3_0}\right)^{1/2}\left( \frac{r}{a_0}\right) e^{-r/2a_0}\cos\theta. \label{4.6.26}\]

פונקציות הגל עבור \(m\) הערכים האחרים,\(\psi_{21\pm 1}(r,\theta,\phi)\), יש \(\psi_{210}\) להחליף את \(\cos\theta\) ה-in \(\mp (1/\sqrt{2})\sin\theta e^{\pm i\phi}\) בהתאמה (מהדיון הקודם \(Y^m_l\) ב-'s).

\(n=2\)למדינה האחרת יש \(l=0\), כך מ\(n=k+l+1\), יש לנו \(k=1\) ולסדרה \(w\) יש שני מונחים\(k=1\), \(k=0\) והיחס הוא

\[ \frac{w_{k+1}}{w_k}=\frac{2(k+l+1-n)}{(k+1)(k+2(l+1))}=-1 \label{4.6.27}\]

עבור הערכים הרלוונטיים:\(k=0, l=0, n=2\). אז\(w_1=-w_0\),\(w(\rho)=w_0(1-\rho)\). עבור\(n=2\),\(\rho=r/2a_0\), פונקציית הגל המנורמלת היא

\[ \psi_{200}(r)=\left( \frac{1}{32\pi a^3_0}\right)^{1/2}\left( 2-\frac{r}{a_0}\right) e^{-r/2a_0}. \label{4.6.28}\]

שים לב שפונקציות גל המומנטום הזוויתי האפס אינן אפס ויש להן שיפוע שאינו אפס במקור. המשמעות היא שלפונקציות הגל התלת מימדיות המלאות יש שם חוסר רציפות בשיפוע! אבל זה בסדר - הפוטנציאל הוא אינסופי במקור. (למעשה, הפרוטון אינו מטען נקודתי, כך שבאמת הקינק יוחלק על נפח בגודל הפרוטון - אפקט זעיר מאוד.)

פתרון כללי של המשוואה הרדיאלית

בפועל, \(w(\rho)\) ניתן לבנות את הפונקציות הרדיאליות הראשונות די בקלות בשיטה שהוצגה לעיל, אך יש לציין כי המשוואה הדיפרנציאלית עבור \(w(\rho)\) \[ \rho \frac{d^2w(\rho)}{d\rho^2}+2(l+1-\rho)\frac{dw(\rho)}{d\rho}+2(n-(l+1))w(\rho)=0 \label{4.6.29}\]

היא למעשה המשוואה של לפלס, בדרך כלל כתובה \[ \left( z\frac{d^2}{dz^2}+(k-1-z)\frac{d}{dz}+p\right) L^k_p(z)=0 \label{4.6.30}\]

איפה מספרים \(k,p\) שלמים, \(L^k_p(z)\) והוא פולינום Laguerre (משיח, עמוד 482).

שתי המשוואות זהות אם\(z = 2\rho\), ולכן הפתרון למשוואה הרדיאלית הוא \[ w_{nl}(\rho)=L^{2l+1}_{n-l-1}(2\rho). \label{4.6.31}\]

ציטוט משיח, הפולינומים של לגואר והפולינומים \(L^0_p(z)\) הקשורים ללגואר ניתנים על ידי: \(L^k_p(z)\)

\[ \begin{matrix} L^0_p(z)=e^z\frac{d^p}{dz^p}e^{-z}z^p \\ L^k_p(z)=(-1)^k\frac{d^k}{dz^k}L^0_{p+k}(z). \end{matrix} \label{4.6.32}\]

(ניתן למצוא ייצוגים אלה בצורה מסודרת על ידי פתרון משוואת לפלס באמצעות - הפתעה - טרנספורמציה של לפלס. ראה מרצבאכר לפרטים.) הפולינומים מספקים את יחסי האורתונורמליות (עם אמנת הנורמליזציה של המתמטיקאים)

\[ \int^{\infty}_{0}e^{-z}z^k L^k_p L^k_qdz=\frac{[(p+k)!]^3}{p!}\delta_{pq}. \label{4.6.33}\]

אבל איך הם נראים? הפונקציה \(e^{-z}z^p\) היא אפס במקור (מלבד המקרה הטריוויאלי\(p=0\)) ואפס באינסוף, תמיד חיובי ובעל שיפוע שאינו אפס למעט בערכו המרבי,\(z=p\). \(p\)הנגזרות מביאות אפסים \(p\) מופרדים, נבדקים בקלות על ידי שרטוט העקומות שנוצרו על ידי בידול עוקב. לכן\(L^0_p(z)\), לפולינום של תואר\(p\), יש אפסים חיוביים \(p\) אמיתיים, וערך במקור\(L^0_p(0)=p!\), שכן המונח היחיד שאינו אפס ב \(z=0\) הוא זה שנוצר על ידי כל המפעילים \(p\) הדיפרנציאליים הפועלים על. \(z^p\)

הפולינום המשויך ל- Laguerre נוצר \(L^k_p(z)\) על ידי זמנים מבדילים. \(L^0_{p+k}(z)\) \(k\) עכשיו \(L^0_{p+k}(z)\) יש אפסים חיוביים \(p+k\) אמיתיים, ההבדל זה נותן פולינום בדרגה אחת נמוכה יותר, עם אפסים שחייבים להיות אחד בכל מרווח בין האפסים של. \(L^0_{p+k}(z)\) טיעון זה נשאר תקף להבדלים רצופים, ולכן \(L^k_p(z)\) חייבים להיות אפסים נפרדים \(p\) אמיתיים.

לחבר את כל זה יחד, ולתרגם בחזרה מ- \(\rho\) אל\(r\), הפתרונות הרדיאליים הם:

\[ R_{nl}(r)=Ne^{-r/na_0}(\frac{r}{na_0})^l L^{2l+1}_{n-l-1}(\frac{2r}{na_0}) \label{4.6.34}\]

עם קבוע \(N\) הנורמליזציה. Griffiths (עמוד 141) נותן פרטים נוספים, כולל קבועי הנורמליזציה שעובדו. השתמשנו באלה כדי לשרטט את \(n=3\) המצבים - לתכנן כאן את הפונקציות\(u(r)=rR(r)\), מכיוון שהנורמליזציה היא \(4\pi \int^{\infty}_{0}|u(r)|^2dr=1, u(r)\) נותן מושג טוב יותר באיזה מרחק מהפרוטון סביר להניח שהאלקטרון יימצא.

להלן שלוש פונקציות הגל \(n=3\) הרדיאלי:

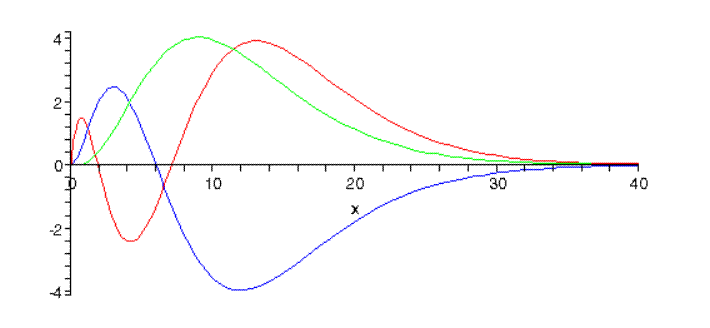
מספר הצמתים, המספר הקוונטי הרדיאלי, הוא\(3-l-1\). (הערה: הנורמליזציות היחסיות נכונות כאן, אך לא הנורמליזציה הכוללת.)

עבור \(n\) ערכים גבוהים יותר, פונקציות הגל מזכירות מכניקה קלאסית. לדוגמה, עבור\(n=10\), התפלגות ההסתברות הגבוהה ביותר של מצב המומנטום הזוויתי מגיעה לשיא ברדיוס \(r=100a_0\) מסלול בוהר:

ואילו עבור\(n=10, l=0\), אנו מוצאים:

שימו לב לשיאים אלה ממש מתחת לרדיוס בוהר כפול. ניתן להבין זאת מהמכניקה הקלאסית: עבור חוק כוח מרובע הפוך, למסלולים אליפטיים עם אותו ציר חציוני יש אותה אנרגיה. \(l=n-1\)המסלול הוא מעגל, \(l=0\) המסלול הוא אליפסה דקה וארוכה (קצה אחד קרוב לפרוטון), ולכן הוא משתרע כמעט פי שניים מהמקור מהמעגל. יתר על כן, האלקטרון המקיף יבלה זמן רב יותר במרחק הרחוק, מכיוון שהוא ינוע לאט מאוד. (הערה: הנורמליזציות בגרפים לעיל הן משוערות בלבד.)