10.5E: תרגילים

Last updated
Save as PDF

Page ID: 205561

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

תרגול הופך למושלם

הכירו את הגרף של משוואה ריבועית בשני משתנים

בתרגילים הבאים, גרף:

דוגמא $\PageIndex{37}$

$y=x^2+3$

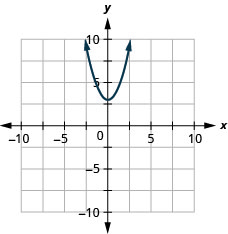
תשובה: $איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש קודקוד ב (0, 3) ועוברת את הנקודה (1, 4).$

דוגמא $\PageIndex{38}$:

$y=−x^2+1$

בתרגילים הבאים, קבע אם הפרבולה נפתחת למעלה או למטה.

דוגמא $\PageIndex{39}$

$y=−2x^2−6x−7$

תשובה: מטה

דוגמא $\PageIndex{40}$:

$y=6x^2+2x+3$

דוגמא $\PageIndex{41}$

y = 4x ^ 2+איקס-4

תשובה: למעלה

דוגמא $\PageIndex{42}$:

$y=−9x^2−24x−16$

מצא את ציר הסימטריה והקודקוד של פרבולה

בתרגילים הבאים, מצא ⓐ את ציר הסימטריה ו ⓑ את הקודקוד.

דוגמא $\PageIndex{43}$

$y=x^2+8x−1$

תשובה: ⓐ איקס=−4 ⓑ (-4, -17)

דוגמא $\PageIndex{44}$:

$y=x^2+10x+25$

דוגמא $\PageIndex{45}$

$y=−x^2+2x+5$

תשובה: ⓐ x = 1 ⓑ (1,6)

דוגמא $\PageIndex{46}$:

$y=−2x^2−8x−3$

מצא את היירוט של פרבולה

בתרגילים הבאים, מצא את יירוט ה - x - ו- y.

דוגמא $\PageIndex{47}$

$y=x^2+7x+6$

תשובה: y: (0,6); איקס: (−1,0), (−6,0)

דוגמא $\PageIndex{48}$:

$y=x^2+10x−11$

דוגמא $\PageIndex{49}$

$y=−x^2+8x−19$

תשובה: y: (0, -19); x: אף אחד

דוגמא $\PageIndex{50}$:

$y=x^2+6x+13$

דוגמא $\PageIndex{51}$

$y=4x^2−20x+25$

תשובה: y: (0,25); איקס: (52,0)

דוגמא $\PageIndex{52}$:

$y=−x^2−14x−49$

גרף משוואות ריבועיות בשני משתנים

בתרגילים הבאים, גרף באמצעות יירוט, קודקוד וציר הסימטריה.

דוגמא $\PageIndex{53}$

$y=x^2+6x+5$

תשובה

y: (0,5); איקס: (−1,0), (-5,0);
ציר: x = −3; קודקוד :( -3, -4)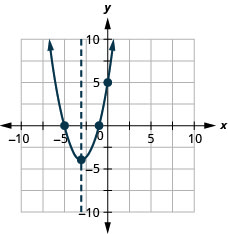

$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (-3, -4) והיירוט (-5, 0), (-1, 0) ו- (0, 5). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה -3.$

דוגמא $\PageIndex{54}$:

$y=x^2+4x−12$

דוגמא $\PageIndex{55}$

$y=x^2+4x+3$

תשובה

y: (0,3); איקס: (−1,0), (−3,0);
ציר: x = -2; קודקוד :( -2, -1)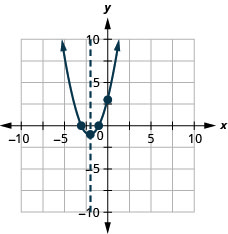

$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (-2, -1) והיירוט (-1, 0), (-3, 0) ו- (0, 3). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה -2.$

דוגמא $\PageIndex{56}$:

$y=x^2−6x+8$

דוגמא $\PageIndex{57}$

$y=9x^2+12x+4$

תשובה

y: (0,4); x:$(−\frac{2}{3},0)$;
ציר:$(−\frac{2}{3}$; קודקוד: $(−\frac{2}{3},0)$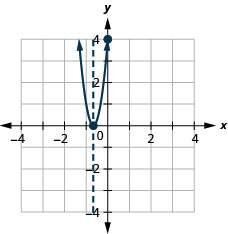

$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -5 ל -5. ציר ה- y של המטוס עובר בין -5 ל -5. לפרבולה יש נקודות המתוות בקודקוד (-2 שלישים, 0) והיירוט (0, 4). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך הקודקוד ב- x שווה ל -2 שלישים.$

דוגמא $\PageIndex{58}$:

$y=−x^2+8x−16$

דוגמא $\PageIndex{59}$

$y=−x^2+2x−7$

תשובה

y: (0, -7); x: אף אחד;
ציר: x = 1; קודקוד :( 1, −6)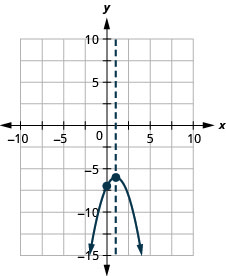

$איור זה מציג פרבולה הנפתחת כלפי מטה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -15 ל -5. לפרבולה יש נקודות המתוות בקודקוד (1, -6) והיירוט (0, -7). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה 1.$

דוגמא $\PageIndex{60}$:

$y=5x^2+2$

דוגמא $\PageIndex{61}$

$y=2x^2−4x+1$

תשובה: y: (0,1); x: (1.7,0), (0.3,0);
ציר: x = 1; קודקוד :( 1, -1)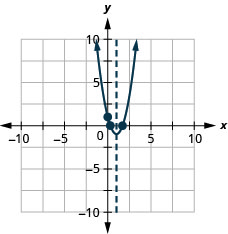
$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (1, -1) והיירוט (1.7, 0), (0.3, 0) ו- (0, 1). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה 1.$

דוגמא $\PageIndex{62}$:

$y=−4x^2−6x−2$

דוגמא $\PageIndex{63}$

$y=−x^2−4x+2$

תשובה

y: (0,2); איקס: (-4.4,0), (0.4,0);
ציר: x = -2; קודקוד :( −2,6)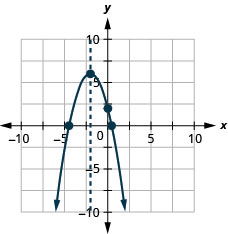

$איור זה מציג פרבולה הנפתחת כלפי מטה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (-2, 6) והיירוט (-4.4, 0), (0.4, 0) ו- (0, 2). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה -2.$

דוגמא $\PageIndex{64}$:

$y=x^2+6x+8$

דוגמא $\PageIndex{65}$

$y=5x^2−10x+8$

תשובה

y: (0,8); x: אין;
ציר: x = 1; קודקוד: (1,3)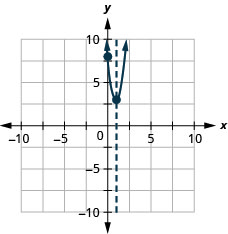

$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (1, 3) והיירוט (0, 8). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה 1.$

דוגמא $\PageIndex{66}$:

$y=−16x^2+24x−9$

דוגמא $\PageIndex{67}$

$y=3x^2+18x+20$

תשובה

y: (0,20); איקס: (-4.5,0), (-1.5,0)
ציר: x = -3; קודקוד :( -3, -7)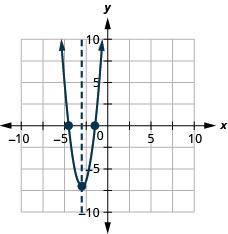

$איור זה מציג פרבולה הנפתחת כלפי מעלה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -10. ציר ה- y של המטוס עובר בין -10 ל -10. לפרבולה יש נקודות המתוות בקודקוד (-3, -7) והיירוט (-4.5, 0) ו- (-1.5, 0). כמו כן על הגרף קו אנכי מקווקו המייצג את ציר הסימטריה. הקו עובר דרך קודקוד ב x שווה -3.$

דוגמא $\PageIndex{68}$:

$y=−2x^2+8x−10$

לפתור יישומים מקסימליים ומינימליים

בתרגילים הבאים, מצא את הערך המקסימלי או המינימלי.

דוגמא $\PageIndex{69}$

$y=2x^2+x−1$

תשובה: הערך המינימלי הוא $−\frac{9}{8}$ מתי$x=−\frac{1}{4}$.

דוגמא $\PageIndex{70}$:

$y=−4x^2+12x−5$

דוגמא $\PageIndex{71}$

$y=x^2−6x+15$

תשובה: הערך המינימלי הוא 6 כאשר x = 3.

דוגמא $\PageIndex{72}$:

$y=−x^2+4x−5$

דוגמא $\PageIndex{73}$

$y=−9x^2+16$

תשובה: הערך המרבי הוא 16 כאשר x = 0.

דוגמא $\PageIndex{74}$:

$y=4x^2−49$

בתרגילים הבאים, לפתור. תשובות עגולות לעשירית הקרובה ביותר.

דוגמא $\PageIndex{75}$

חץ נורה אנכית כלפי מעלה מרציף בגובה 45 רגל בקצב של 168 רגל/שנייה. השתמש במשוואה הריבועית $h=−16t^2+168t+45$ כדי למצוא כמה זמן ייקח לחץ להגיע לגובה המרבי שלו ואז מצא את הגובה המרבי.

תשובה: תוך 5.3 שניות החץ יגיע לגובה מרבי של 486 רגל.

דוגמא $\PageIndex{76}$:

אבן נזרקת אנכית כלפי מעלה מרציף שגובהו 20 רגל בקצב של 160 רגל לשנייה. השתמש במשוואה הריבועית $h=−16t^2+160t+20$ כדי למצוא כמה זמן ייקח לאבן להגיע לגובה המרבי שלה ואז מצא את הגובה המרבי.

דוגמא $\PageIndex{77}$

בעל חנות מחשבים מעריך כי על ידי חיוב של x דולר כל אחד עבור מחשב מסוים, הוא יכול למכור $40−x$ מחשבים בכל שבוע. המשוואה הריבועית $R=−x^2+40x$ משמשת למציאת ההכנסות, R, שהתקבלו כאשר מחיר המכירה של מחשב הוא x מצא את מחיר המכירה שייתן לו את ההכנסה המרבית ואז מצא את סכום ההכנסה המרבית.

תשובה: 20 מחשבים יתנו את המקסימום של 400$ בקבלה.

דוגמא $\PageIndex{78}$:

קמעונאי שמוכר תרמילים מעריך כי על ידי מכירתם תמורת x דולר כל אחד, הוא יוכל למכור $100−x$ תרמילים בחודש. המשוואה הריבועית $R=−x^2+100x$ משמשת למציאת ה- R שהתקבל כאשר מחיר המכירה של תרמיל הוא x מצא את מחיר המכירה שייתן לו את ההכנסה המרבית ואז מצא את סכום ההכנסה המרבית.

דוגמא $\PageIndex{79}$

חוואי עומד לגדר שלושה צדדים של מכלאה ליד נהר. הוא צריך למקסם את שטח המכלאה באמצעות 240 רגל של גידור. המשוואה הריבועית א=איקס (240−2x) נותנת את שטח המכלאה, A, לאורך, x, של המכלאה לאורך הנהר. מצא את אורך המכלאה לאורך הנהר שייתן את השטח המרבי ואז מצא את השטח המרבי של המכלאה.

תשובה: אורך הצד לאורך נהר המכלאה הוא 120 רגל והשטח המרבי הוא 7,200 רגל רבוע.

דוגמא $\PageIndex{80}$:

וטרינר סוגר אזור ריצה חיצוני מלבני נגד הבניין שלו עבור הכלבים שהוא מטפל בהם. הוא צריך למקסם את השטח באמצעות 100 רגל של גידור. המשוואה הריבועית $A=x(100−2x)$ נותנת את השטח, A, של ריצת הכלב לאורך, x, של הבניין שיגבול בריצת הכלבים. מצא את אורך הבניין שאמור לגבול את ריצת הכלב כדי לתת את השטח המרבי, ואז מצא את השטח המרבי של ריצת הכלבים.

מתמטיקה יומיומית

דוגמא $\PageIndex{81}$

במערך התרגילים הקודם עבדת עם המשוואה הריבועית $R=−x^2+40x$ שעיצבה את ההכנסות שהתקבלו ממכירת מחשבים במחיר של x דולר. מצאת את מחיר המכירה שייתן את ההכנסה המרבית וחישבת את ההכנסה המרבית. עכשיו תוכלו להסתכל על מאפיינים נוספים של מודל זה.
1. גרף את המשוואה$R=−x^2+40x$.

2. מצא את הערכים של x -יירוט.

תשובה

1.
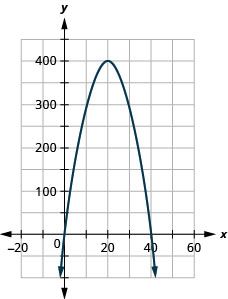
$איור זה מציג פרבולה הנפתחת כלפי מטה בתרשים במישור הקואורדינטות x y. ציר ה- x של המטוס עובר בין -10 ל -60. ציר ה- y של המטוס עובר בין -50 ל -500. לפרבולה יש קודקוד ב (20, 400) וגם עובר את הנקודות (0, 0) ו- (40, 0).$

2. (0,0), (40,0)

דוגמא $\PageIndex{82}$:

במערך התרגילים הקודם עבדת עם המשוואה הריבועית $R=−x^2+100x$ שעיצבה את ההכנסות שהתקבלו ממכירת תרמילים במחיר של x דולר. מצאת את מחיר המכירה שייתן את ההכנסה המרבית וחישבת את ההכנסה המרבית. עכשיו תוכלו להסתכל על מאפיינים נוספים של מודל זה.

1. גרף את המשוואה$R=−x^2+100x$.

2. מצא את הערכים של x -יירוט.

תרגילי כתיבה

דוגמא $\PageIndex{83}$

עבור מודל ההכנסות בפעילות גופנית ופעילות גופנית, הסבר מה המשמעות של יירוט x לבעל חנות המחשבים.

תשובה: התשובות ישתנו.

דוגמא $\PageIndex{84}$:

למודל ההכנסות בפעילות גופנית ופעילות גופנית, הסבירו מה המשמעות של יירוט ה - x עבור קמעונאי התרמילים.

בדיקה עצמית

א. לאחר השלמת התרגילים, השתמש ברשימת בדיקה זו כדי להעריך את שליטתך ביעדי סעיף זה.

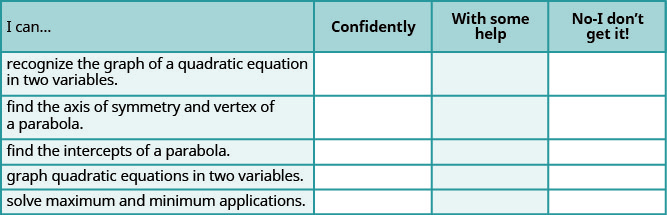
$טבלה זו כוללת שש שורות וארבע עמודות. השורה הראשונה היא שורת כותרת והיא מתייגת כל עמודה. העמודה הראשונה מסומנת "אני יכול...", השנייה "בביטחון", השלישית "עם קצת עזרה" והאחרונה "לא - אני לא מבין את זה". בעמודה "אני יכול..." בשורה השנייה כתוב "לפתור משוואות ריבועיות באמצעות הריבוע עבור לזהות את הגרף של משוואה ריבועית בשני משתנים." בשורה השלישית כתוב "מצא את ציר הסימטריה והקודקוד של פרבולה." בשורה הרביעית כתוב "מצא את היירוט של פרבולה." בשורה החמישית כתוב "משוואות ריבועיות גרף בשני משתנים." ובשורה האחרונה כתוב "לפתור יישומים מקסימליים ומינימליים." שאר העמודות ריקות.$

ב. מה רשימת הבדיקה הזו אומרת לך על השליטה שלך בסעיף זה? אילו צעדים תנקוט כדי לשפר?

תרגול הופך למושלם

דוגמא \(\PageIndex{37}\)

דוגמא \(\PageIndex{38}\):

דוגמא \(\PageIndex{39}\)

דוגמא \(\PageIndex{40}\):

דוגמא \(\PageIndex{41}\)

דוגמא \(\PageIndex{42}\):

דוגמא \(\PageIndex{43}\)

דוגמא \(\PageIndex{44}\):

דוגמא \(\PageIndex{45}\)

דוגמא \(\PageIndex{46}\):

דוגמא \(\PageIndex{47}\)

דוגמא \(\PageIndex{48}\):

דוגמא \(\PageIndex{49}\)

דוגמא \(\PageIndex{50}\):

דוגמא \(\PageIndex{51}\)

דוגמא \(\PageIndex{52}\):

דוגמא \(\PageIndex{53}\)

דוגמא \(\PageIndex{54}\):

דוגמא \(\PageIndex{55}\)

דוגמא \(\PageIndex{56}\):

דוגמא \(\PageIndex{57}\)

דוגמא \(\PageIndex{58}\):

דוגמא \(\PageIndex{59}\)

דוגמא \(\PageIndex{60}\):

דוגמא \(\PageIndex{61}\)

דוגמא \(\PageIndex{62}\):

דוגמא \(\PageIndex{63}\)

דוגמא \(\PageIndex{64}\):

דוגמא \(\PageIndex{65}\)

דוגמא \(\PageIndex{66}\):

דוגמא \(\PageIndex{67}\)

דוגמא \(\PageIndex{68}\):

דוגמא \(\PageIndex{69}\)

דוגמא \(\PageIndex{70}\):

דוגמא \(\PageIndex{71}\)

דוגמא \(\PageIndex{72}\):

דוגמא \(\PageIndex{73}\)

דוגמא \(\PageIndex{74}\):

דוגמא \(\PageIndex{75}\)

דוגמא \(\PageIndex{76}\):

דוגמא \(\PageIndex{77}\)

דוגמא \(\PageIndex{78}\):

דוגמא \(\PageIndex{79}\)

דוגמא \(\PageIndex{80}\):

מתמטיקה יומיומית

דוגמא \(\PageIndex{81}\)

דוגמא \(\PageIndex{82}\):

תרגילי כתיבה

דוגמא \(\PageIndex{83}\)

דוגמא \(\PageIndex{84}\):

בדיקה עצמית