10.5: גרף משוואות ריבועיות
- Page ID
- 205556
בסוף פרק זה, תוכל:
- הכירו את הגרף של משוואה ריבועית בשני משתנים
- מצא את ציר הסימטריה והקודקוד של פרבולה
- מצא את היירוט של פרבולה
- גרף משוואות ריבועיות בשני משתנים
- לפתור יישומים מקסימליים ומינימליים
הכירו את הגרף של משוואה ריבועית בשני משתנים
יש לנו תרשים משוואות של הטופס\(Ax+By=C\). קראנו למשוואות כמו משוואות לינאריות אלה מכיוון שהגרפים שלהם הם קווים ישרים.
כעת, נגרף משוואות של הטופס\(y=ax^2+bx+c\). אנו מכנים משוואה מסוג זה משוואה ריבועית בשני משתנים.
משוואה ריבועית בשני משתנים, כאשר a, b ו- c הם מספרים ממשיים והיא \(a\neq 0\) משוואה של הצורה \[y=ax^2+bx+c \nonumber\]
בדיוק כמו שהתחלנו לשרטט משוואות לינאריות על ידי התוויית נקודות, נעשה את אותו הדבר עבור משוואות ריבועיות.
בואו נסתכל תחילה על גרף המשוואה הריבועית. \(y=x^2\) אנו נבחר ערכים שלמים של x בין -2 ל -2 ונמצא את ערכי y שלהם. ראה טבלה.
| \(y=x^2\) | |
| x | y |
| 0 | 0 |
| 1 | 1 |
| \(−1\) | 1 |
| 2 | 4 |
| \(−2\) | 4 |
שימו לב כאשר אנו נותנים \(x=1\) ו\(x=−1\), קיבלנו את אותו ערך עבור y.
\[\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}\]
אותו דבר קרה כאשר נתנו \(x=2\) ו\(x=−2\).
כעת, נתווה את הנקודות כדי להציג את הגרף של\(y=x^2\). ראה איור.
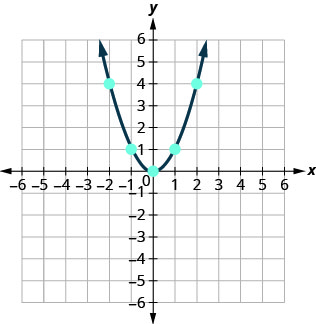
הגרף אינו קו. נתון זה נקרא פרבולה. לכל משוואה ריבועית יש גרף שנראה כך.
בדוגמה תתרגל גרף של פרבולה על ידי התוויית מספר נקודות.
\(y=x^2-1\)
- תשובה
-
נגרף את המשוואה על ידי תכנון נקודות.
בחר ערכים שלמים עבור x, החלף אותם במשוואה ופתור עבור y.רשום את הערכים של הזוגות המסודרים בתרשים. 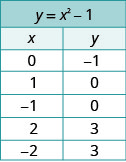
התווה את הנקודות ואז חבר אותן עם עקומה חלקה. התוצאה תהיה הגרף של המשוואה \(y=x^2−1\) 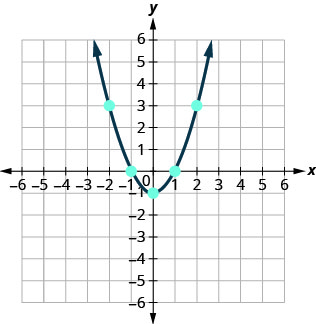
גרף\(y=−x^2\).
- תשובה
-
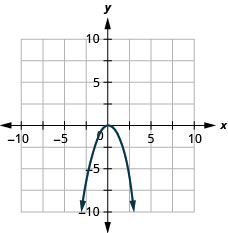
גרף\(y=x^2+1\).
- תשובה
-
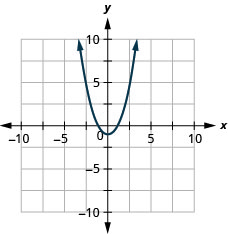
איך לעשות את המשוואות \(y=x^2\) ו \(y=x^2−1\) differ? What is the difference between their graphs? How are their graphs the same?
כל הפרבולות של הטופס \(y=ax^2+bx+c\) נפתחות כלפי מעלה או מטה. ראה איור.
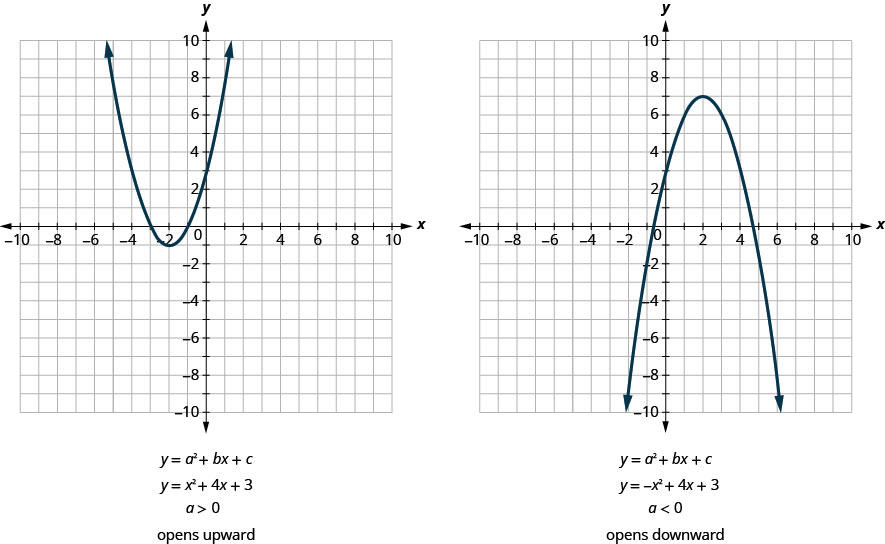
שימו לב שההבדל היחיד בשתי המשוואות הוא הסימן השלילי לפני \(x^2\) במשוואה של הגרף השני באיור. כאשר \(x^2\) המונח חיובי, הפרבולה נפתחת כלפי מעלה, וכאשר \(x^2\) המונח שלילי, הפרבולה נפתחת כלפי מטה.
למשוואה הריבועית\(y=ax^2+bx+c\), אם:

קבע אם כל פרבולה נפתחת כלפי מעלה או מטה:
- \(y=−3x^2+2x−4\)
- \( y=6x^2+7x−9\)
- תשובה
-
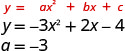
מכיוון שה- "a" שלילי, הפרבולה תיפתח כלפי מטה.
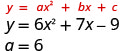
מכיוון שה- "a" חיובי, הפרבולה תיפתח כלפי מעלה.
קבע אם כל פרבולה נפתחת כלפי מעלה או מטה:
- \(y=2x^2+5x−2\)
- \(y=−3x^2−4x+7\)
- תשובה
-
- למעלה
- מטה
קבע אם כל פרבולה נפתחת כלפי מעלה או מטה:
- \(y=−2x^2−2x−3\)
- \(y=5x^2−2x−1\)
- תשובה
-
- מטה
- למעלה
מצא את ציר הסימטריה והקודקוד של פרבולה
תסתכל שוב על איור. האם אתה רואה שנוכל לקפל כל פרבולה לשניים ושצד אחד ישכב על גבי השני? 'קו הקיפול' הוא קו סימטריה. אנו קוראים לזה ציר הסימטריה של הפרבולה.
אנו מראים שוב את אותם שני גרפים עם ציר הסימטריה באדום. ראה איור.
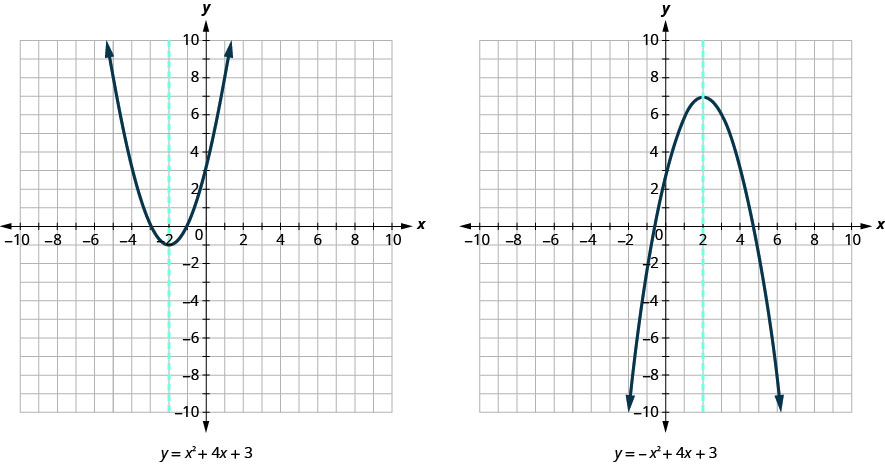
ניתן לגזור את משוואת ציר הסימטריה באמצעות הנוסחה הריבועית. נשמיט את הגזירה כאן ונמשיך ישירות לשימוש בתוצאה. המשוואה של ציר הסימטריה של הגרף של \(y=ax^2+bx+c\) היא x =\(−\frac{b}{2a}\).
לכן, כדי למצוא את משוואת הסימטריה של כל אחת מהפרבולות שציירנו לעיל, נחליף בנוסחה x =. \(−\frac{b}{2a}\)
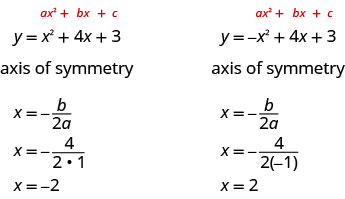
הנקודה על הפרבולה שנמצאת על ציר הסימטריה היא הנקודה הנמוכה ביותר או הגבוהה ביותר בפרבולה, תלוי אם הפרבולה נפתחת כלפי מעלה או מטה. נקודה זו נקראת קודקוד הפרבולה.
אנו יכולים למצוא בקלות את הקואורדינטות של הקודקוד, מכיוון שאנו יודעים שהוא נמצא על ציר הסימטריה. המשמעות היא שקואורדינטת ה- x שלה היא\(−\frac{b}{2a}\). כדי למצוא את קואורדינטת y של הקודקוד, אנו מחליפים את הערך של קואורדינטת x במשוואה הריבועית.

לפרבולה עם משוואה\(y=ax^2+bx+c\):
- ציר הסימטריה של פרבולה הוא הקו x \(−\frac{b}{2a}\) =.
- הקודקוד נמצא על ציר הסימטריה, כך שקואורדינטת ה - x שלו היא. \(−\frac{b}{2a}\)
כדי למצוא את קואורדינטת y של הקודקוד, אנו מחליפים x = \(−\frac{b}{2a}\) למשוואה הריבועית.
עבור הפרבולה \(y=3x^2−6x+2\) מצא:
- ציר הסימטריה ו
- הקודקוד.
- תשובה
-
1. 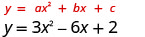
ציר הסימטריה הוא הקו x = \(−\frac{b}{2a}\) 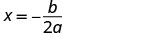
החלף את הערכים של a, b במשוואה. 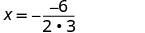
לפשט איקס=1 ציר הסימטריה הוא הקו איקס=1 2. 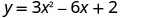
הקודקוד נמצא על קו הסימטריה, כך שקואורדינטת ה - x שלו תהיה x = 1 החלף x = 1 למשוואה ופתור עבור y. 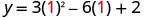
לפשט 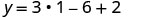
זהו ה- y -קואורדינטה. y=−1
הקודקוד הוא (1, −1).
עבור הפרבולה \(y=2x^2−8x+1\) מצא:
- ציר הסימטריה ו
- הקודקוד.
- תשובה
-
- איקס=2
- (2, −7)
עבור הפרבולה \(y=2x^2−4x−3\) מצא:
- ציר הסימטריה ו
- הקודקוד.
- תשובה
-
- איקס=1
- (1, -5)
מצא את היירוט של פרבולה
כאשר שרטטנו משוואות לינאריות, השתמשנו לעתים קרובות ביירוטים x - ו- y כדי לעזור לנו לשרטט את הקווים. מציאת הקואורדינטות של היירוטים תעזור לנו גם לשרטט פרבולות.
זכור, ביירוט y הערך של x הוא אפס. לכן, כדי למצוא את יירוט y, אנו מחליפים x = 0 במשוואה.
בואו נמצא את יירוט ה- y של שתי הפרבולות המוצגות באיור למטה.
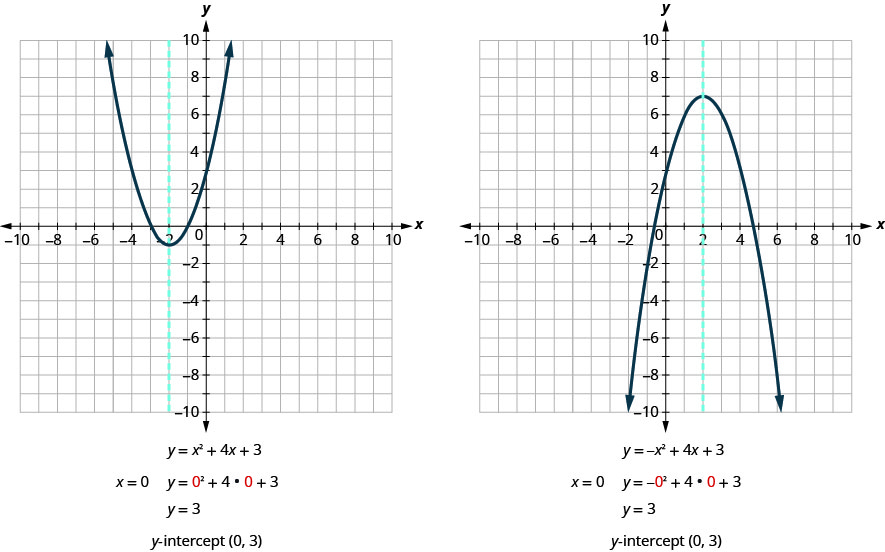
ביירוט x, הערך של y הוא אפס. כדי למצוא יירוט x, אנו מחליפים \(y=0\) למשוואה. במילים אחרות, נצטרך לפתור את המשוואה \(0=ax^2+bx+c\) עבור x.
\[\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}\]
אבל פתרון משוואות ריבועיות כמו זה הוא בדיוק מה שעשינו קודם בפרק זה.
כעת אנו יכולים למצוא את x -יירוט של שתי הפרבולות המוצגות באיור.
ראשית, נמצא את ה - x -יירוט של פרבולה עם משוואה. \(y=x^2+4x+3\)
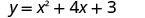 |
||
| תן y = 0 | 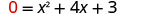 |
|
| פקטור. | 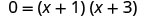 |
|
| השתמש במאפיין המוצר אפס. | 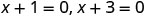 |
|
| לפתור. | 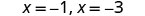 |
|
| ה איקס יירוט הם (-1,0) ו- (-3,0). | ||
כעת, נמצא את יירוט ה - x של הפרבולה עם משוואה. \(y=−x^2+4x+3\)
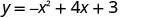 |
||
| תן y = 0 | 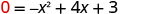 |
|
| ריבועי זה אינו גורם, ולכן אנו משתמשים בנוסחה הריבועית. | 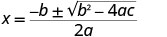 |
|
| א=−1, ב=4, ג=3. | 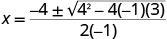 |
|
| לפשט. | 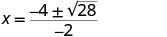 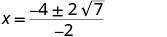 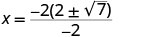 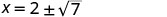 |
|
| יירוט ה- x הוא ו \((2+\sqrt{7},0)\) \((2−\sqrt{7},0)\) | ||
נשתמש בקירובים העשרוניים של יירוט ה- x, כך שנוכל לאתר נקודות אלה בתרשים.
\[\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}\]
האם התוצאות הללו תואמות את הגרפים שלנו? ראה איור.
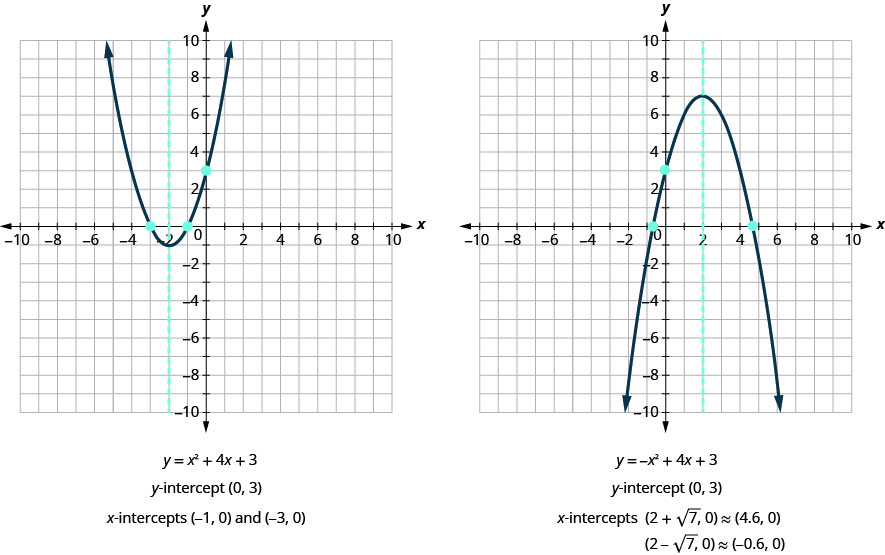
כדי למצוא את היירוט של פרבולה עם משוואה: \(y=ax^2+bx+c\)
\[\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}\]
מצא את היירוט של הפרבולה. \(y=x^2−2x−8\)
- תשובה
-
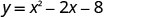
כדי למצוא את יירוט y, תן x = 0 ולפתור עבור y. 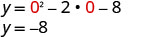
כאשר איקס=0, אז y = −8.
יירוט y הוא הנקודה (0, −8).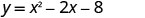
כדי למצוא את x -יירוט, תן y = 0 ולפתור עבור x. 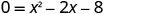
לפתור על ידי פקטורינג. 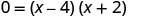
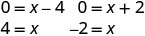
- מתי y=0, אז איקס=4 או איקס=−2. ה איקס -יירוט הם הנקודות (4,0) ו- (-2,0).
מצא את היירוט של הפרבולה. \(y=x^2+2x−8\)
- תשובה
-
y: (0, -8); איקס: (-4,0), (2,0)
מצא את היירוט של הפרבולה. \(y=x^2−4x−12\)
- תשובה
-
y: (0, -12); איקס: (6,0), (-2,0)
בפרק זה פתרנו משוואות ריבועיות של הצורה\(ax^2+bx+c=0\). פתרנו עבור xx והתוצאות היו הפתרונות למשוואה.
כעת אנו בוחנים משוואות ריבועיות בשני משתנים מהצורה\(y=ax^2+bx+c\). הגרפים של משוואות אלה הם פרבולות. ה-x -יירוט של הפרבולות מתרחש כאשר y=0.
לדוגמה:
\[\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}\]
הפתרונות של המשוואה הריבועית הם ערכי ה- x של ה- x -יירוט.
מוקדם יותר ראינו שלמשוואות ריבועיות יש 2, 1 או 0 פתרונות. הגרפים שלהלן מציגים דוגמאות לפרבולות לשלושת המקרים הללו. מכיוון שפתרונות המשוואות נותנים את ה - x -יירוט של הגרפים, מספר ה - x -יירוט זהה למספר הפתרונות.
בעבר השתמשנו במפלה כדי לקבוע את מספר הפתרונות של משוואה ריבועית של הטופס. \(ax^2+bx+c=0\) כעת, אנו יכולים להשתמש במפלה כדי לומר לנו כמה x -יירוט יש בגרף.
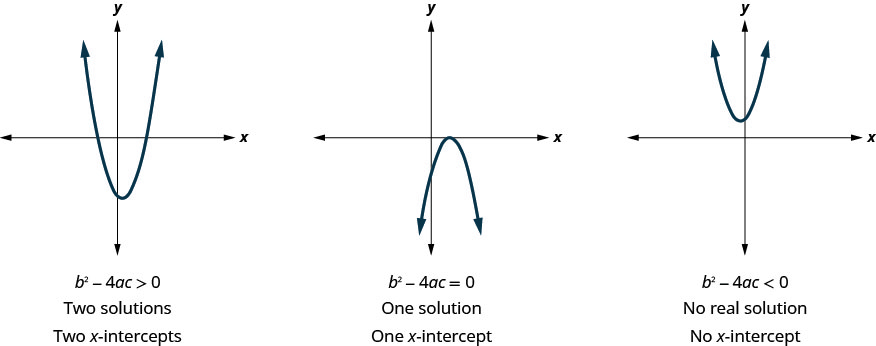
לפני שתתחיל לפתור את המשוואה הריבועית כדי למצוא את ערכי ה - x -יירוט, ייתכן שתרצה להעריך את המפלה כדי שתדע לכמה פתרונות לצפות.
מצא את היירוט של הפרבולה. \(y=5x^2+x+4\)
- תשובה
-
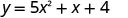
כדי למצוא את יירוט y, תן x = 0 ולפתור עבור y. 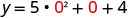

כאשר x = 0, אז y = 4.
יירוט y הוא הנקודה (0,4).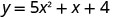
כדי למצוא את x -יירוט, תן y = 0 ולפתור עבור x. 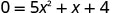
מצא את הערך של המפלה כדי לחזות את מספר הפתרונות וכך x -מיירט. ב^2-4ac
1^2−4⋅5⋅4
1—80
-79
מכיוון שערכו של המפלה הוא שלילי, אין פיתרון אמיתי למשוואה. אין x -יירוט.
מצא את היירוט של הפרבולה. \(y=3x^2+4x+4\)
- תשובה
-
y: (0,4); x: אף אחד
מצא את היירוט של הפרבולה. \(y=x^2−4x−5\)
- תשובה
-
y: (0, -5); איקס: (5,0) (−1,0)
מצא את היירוט של הפרבולה. \(y=4x^2−12x+9\)
- תשובה
-
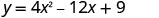
כדי למצוא את יירוט y, תן x = 0 ולפתור עבור y. 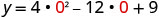

כאשר x = 0, אז y = 9.
יירוט y הוא הנקודה (0,9).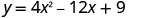
כדי למצוא את x -יירוט, תן y = 0 ולפתור עבור x. 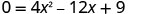
מצא את הערך של המפלה כדי לחזות את מספר הפתרונות וכך x -מיירט. ב^2-4ac
12 ^ 2−4⋅4⋅9
144—144
0
מכיוון שערכו של המפלה הוא 0, אין פיתרון אמיתי למשוואה. אז יש אחד x -יירוט. לפתור את המשוואה על ידי פקטורינג הטרינום המרובע המושלם. 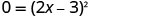
השתמש במאפיין מוצר אפס. 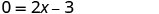
לפתור עבור x. 

כאשר y = 0, אז \(\frac{3}{2}\) = x. יירוט ה- x הוא הנקודה. \((\frac{3}{2},0)\)
מצא את היירוט של הפרבולה. \(y=−x^2−12x−36.\)
- תשובה
-
y: (0, −36); איקס: (−6,0)
מצא את היירוט של הפרבולה. \(y=9x^2+12x+4\)
- תשובה
-
y: (0,4); x: \((−\frac{2}{3},0)\)
גרף משוואות ריבועיות בשני משתנים
עכשיו, יש לנו את כל החלקים שאנחנו צריכים כדי לשרטט משוואה ריבועית בשני משתנים. אנחנו רק צריכים לחבר אותם יחד. בדוגמה הבאה נראה כיצד לעשות זאת.
כיצד לשרטט משוואה ריבועית בשני משתנים
גרף\(y=x2−6x+8\).
- תשובה
-


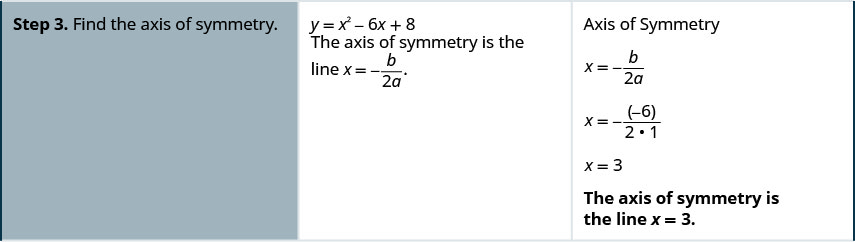




גרף את הפרבולה \(y=x^2+2x−8\).
- תשובה
-
y: (0, -8); x: (2,0), (-4,0);
ציר: x = -1; קודקוד: (-1, -9);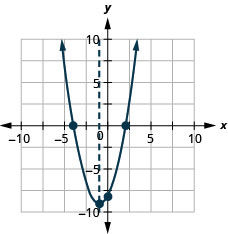
גרף את הפרבולה\(y=x^2−8x+12\).
- תשובה
-
y: (0,12); x: (2,0), (6,0);
ציר: x = 4; קודקוד :( 4, -4);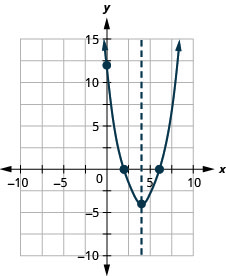
- כתוב את המשוואה הריבועית עם yy בצד אחד.
- קבע אם הפרבולה נפתחת כלפי מעלה או מטה.
- מצא את ציר הסימטריה.
- מצא את הקודקוד.
- מצא את יירוט y. מצא את הנקודה סימטרית ליירוט y על פני ציר הסימטריה.
- מצא את ה - x -יירוט.
- גרף את הפרבולה.
הצלחנו למצוא את ה - x -יירוט בדוגמה האחרונה על ידי פקטורינג. אנו מוצאים את ה - x -יירוט בדוגמה הבאה גם על ידי פקטורינג.
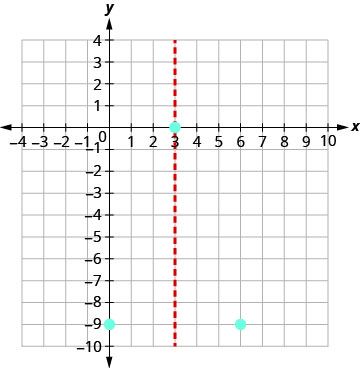
גרף\(y=−x^2+6x−9\).
- תשובה
-
המשוואה y יש בצד אחד. 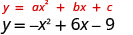
מכיוון ש- a הוא -1, הפרבולה נפתחת כלפי מטה.
כדי למצוא את ציר הסימטריה, מצא\(x=−\frac{b}{2a}\).
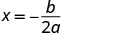
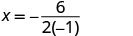

ציר הסימטריה הוא איקס=3. הקודקוד נמצא על הקו x = 3.
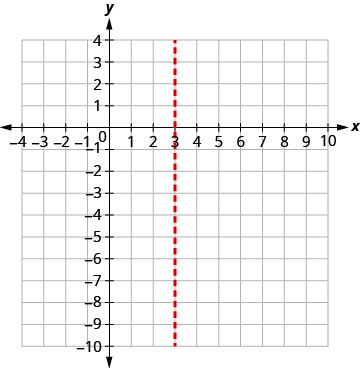
מצא את y כאשר x = 3.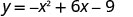
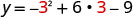
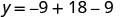

הקודקוד הוא (3,0).
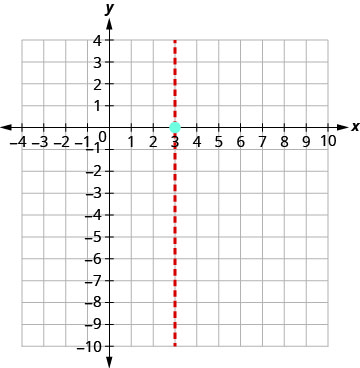
יירוט y מתרחש כאשר x = 0.
תחליף x = 0.
לפשט.
הנקודה (0, -9) היא שלוש יחידות משמאל לקו הסימטריה.
הנקודה שלוש יחידות מימין לקו הסימטריה היא (6, -9).
נקודה סימטרית ליירוט y היא (6, −9)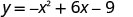
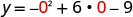

(0, -9).
ה איקס -יירוט מתרחש כאשר y = 0. 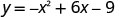
תחליף y = 0. 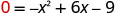
גורם ה- GCF. 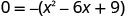
פקטור הטרינום. 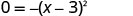
לפתור עבור x. 
חבר את הנקודות כדי לתאר את הפרבולה. 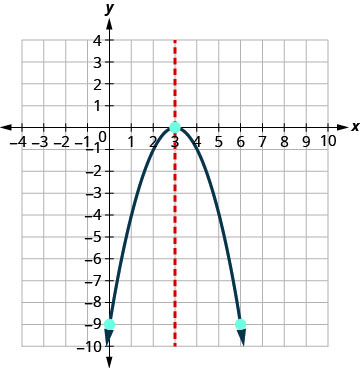
גרף את הפרבולה\(y=−3x^2+12x−12\).
- תשובה
-
y: (0, -12); x: (2,0);
ציר: x = 2; קודקוד: (2,0);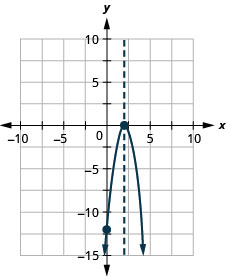
גרף את הפרבולה\(y=25x^2+10x+1\).
- תשובה
-
y: (0,1); x: (-15,0);
ציר: x = -15; קודקוד :( -15,0);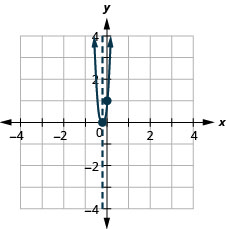
עבור הגרף של \(y=−x^2+6x−9\) the vertex and the x -יירוט היו אותה נקודה. זוכרים כיצד המפלה קובע את מספר הפתרונות של משוואה ריבועית? המפלה של המשוואה \(0=−x^2+6x−9\) is 0, so there is only one solution. That means there is only one x -יירוט, וזה קודקוד הפרבולה.
כמה x -יירוט היית מצפה לראות בגרף של? \(y=x^2+4x+5\)
גרף\(y=x^2+4x+5\).
- תשובה
-
למשוואה יש y בצד אחד. 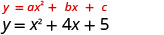
מכיוון ש- a הוא 1, הפרבולה נפתחת כלפי מעלה. 
\(x=−\frac{b}{2a}\). 
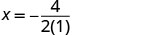

איקס=−2.
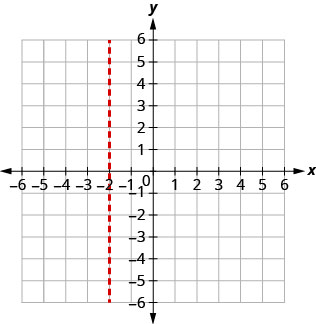
הקודקוד נמצא על הקו איקס=−2. מצא את y כאשר x = −2. 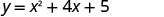
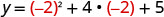
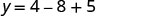

(-2,1).
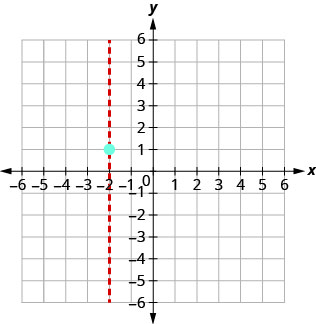
יירוט y מתרחש כאשר x = 0.
תחליף x = 0.
לפשט.
הנקודה (0,5) היא שתי יחידות מימין לקו הסימטריה.
הנקודה שתי יחידות משמאל לקו הסימטריה היא (-4,5).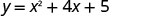
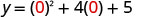

(0,5).
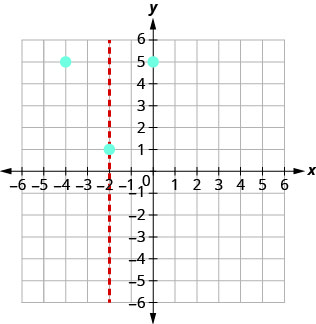
(-4,5)ה איקס - יירוט מתרחש כאשר y = 0. תחליף y = 0.
בדוק את המפלה.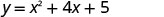
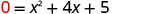
\(b^2−4ac\)
\(42−4⋅15\)
\(16−20\)
\(−4\)מכיוון שערכו של המפלה הוא שלילי, אין פיתרון ולכן אין יירוט x.
חבר את הנקודות כדי לתאר את הפרבולה. ייתכן שתרצה לבחור שתי נקודות נוספות לדיוק רב יותר.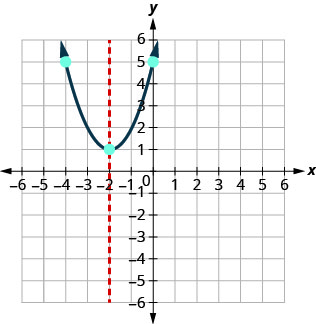
גרף את הפרבולה\(y=2x^2−6x+5\).
- תשובה
-
y: (0,5); x: אין;
ציר:; קודקוד:\(x=\frac{3}{2}\); \((\frac{3}{2},\frac{1}{2})\)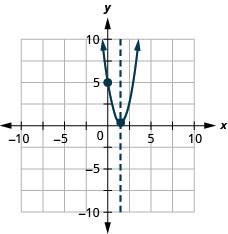
גרף את הפרבולה\(y=−2x^2−1\).
- תשובה
-
y: (0, -1); x: אף אחד;
ציר: x = 0; קודקוד: (0, -1);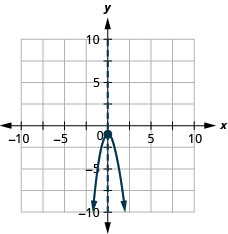
קל למצוא את יירוט y על ידי החלפת איקס=0 במשוואה, לא? אבל היינו צריכים להשתמש בנוסחה הריבועית כדי למצוא את ה - x -יירוט בדוגמה. נשתמש שוב בנוסחה הריבועית בדוגמה הבאה.
גרף\(y=2x^2−4x−3\).
- תשובה
-

למשוואה y יש צד אחד.
מכיוון ש- a הוא 2, הפרבולה נפתחת כלפי מעלה.
כדי למצוא את ציר הסימטריה, מצא \(x=−\frac{b}{2a}\) 


הקודקוד הוא x = 1הקודקוד על הקו איקס=1. 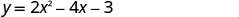
מצא את y כאשר x = 1 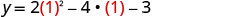


(1, -5)יירוט y מתרחש כאשר x = 0. 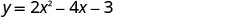
תחליף x = 0. 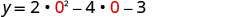
לפשט. 
יירוט ה - y הוא (0, -3)
הנקודה (0, -3) היא יחידה אחת משמאל לקו הסימטריה.
הנקודה יחידה אחת מימין לקו הסימטריה היא (2, -3)נקודה סימטרית ליירוט y היא (2, -3). ה איקס -יירוט מתרחש כאשר y = 0 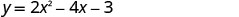
תחליף y = 0 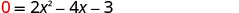
השתמש בנוסחה הריבועית. 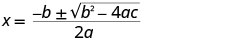
תחליף בערכים של a, b, c. 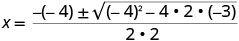
לפשט. 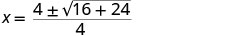
פשט בתוך הרדיקל. 
לפשט את הרדיקלי. 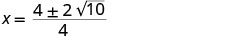
גורם ה- GCF. 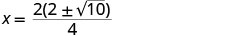
הסר גורמים נפוצים. 
כתוב כשתי משוואות. 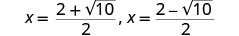
הערך משוער. 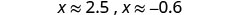
הערכים המשוערים של x- יירוט הם (2.5,0) ו- (-0.6,0). גרף את הפרבולה באמצעות הנקודות שנמצאו. 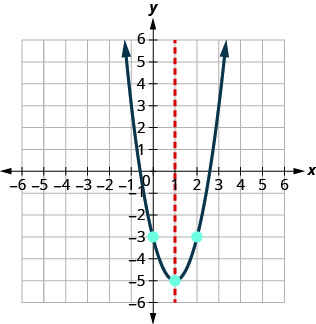
גרף את הפרבולה\(y=5x^2+10x+3\).
- תשובה
-
y: (0,3); איקס: (-1.6,0), (-0.4,0);
ציר: x = -1; קודקוד :( -1, -2);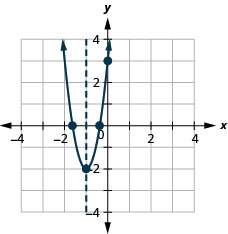
גרף את הפרבולה\(y=−3x^2−6x+5\).
- תשובה
-
y: (0,5); x: (0.6,0), (-2.6,0);
ציר: x = -1; קודקוד :( -1,8);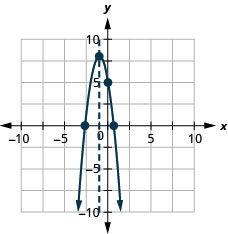
לפתור יישומים מקסימליים ומינימליים
הידיעה שקודקוד הפרבולה הוא הנקודה הנמוכה ביותר או הגבוהה ביותר של הפרבולה נותנת לנו דרך קלה לקבוע את הערך המינימלי או המקסימלי של משוואה ריבועית. קואורדינטת y של הקודקוד היא ערך y המינימלי של פרבולה שנפתחת כלפי מעלה. זהו ערך ה- y המרבי של פרבולה שנפתחת כלפי מטה. ראה איור.
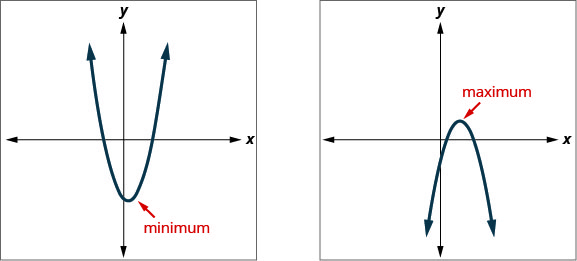
קואורדינטת y של קודקוד הגרף של משוואה ריבועית היא ה
- ערך מינימלי של המשוואה הריבועית אם הפרבולה נפתחת כלפי מעלה.
- הערך המרבי של המשוואה הריבועית אם הפרבולה נפתחת כלפי מטה.
מצא את הערך המינימלי של המשוואה \(y=x^2+2x−8\) הריבועית.
- תשובה
-
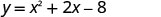
מכיוון ש- a חיובי, הפרבולה נפתחת כלפי מעלה. למשוואה הריבועית יש מינימום. מצא את ציר הסימטריה. 
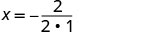

איקס=−1הקודקוד נמצא על הקו איקס=−1. 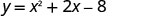
מצא את y כאשר x = −1. 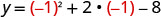
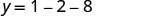

(-1, -9)מכיוון שלפרבולה יש מינימום, קואורדינטת ה - y של הקודקוד היא ערך ה - y המינימלי של המשוואה הריבועית. הערך המינימלי של הריבוע הוא -9 והוא מתרחש כאשר איקס=−1. הצג את הגרף כדי לאמת את התוצאה. 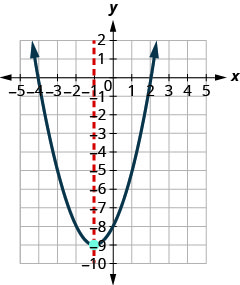
מצא את הערך המקסימלי או המינימלי של המשוואה \(y=x^2−8x+12\) הריבועית.
- תשובה
-
הערך המינימלי הוא -4 כאשר x = 4.
מצא את הערך המקסימלי או המינימלי של המשוואה \(y=−4x^2+16x−11\) הריבועית.
- תשובה
-
הערך המרבי הוא 5 כאשר x = 2.
השתמשנו בנוסחה
\[\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}\]
כדי לחשב את הגובה ברגליים, h, של אובייקט שנורה כלפי מעלה לאוויר במהירות התחלתית,\(v_{0}\), לאחר t שניות.
נוסחה זו היא משוואה ריבועית במשתנה tt, ולכן הגרף שלה הוא פרבולה. על ידי פתרון הקואורדינטות של הקודקוד, אנו יכולים למצוא כמה זמן ייקח לאובייקט להגיע לגובהו המרבי. לאחר מכן, אנו יכולים לחשב את הגובה המרבי.
המשוואה הריבועית \(h=−16t^2+v_{0}t+h_{0}\) מדגמנת את גובה הכדורעף ישר כלפי מעלה במהירות 176 רגל לשנייה מגובה של 4 מטר.
- כמה שניות ייקח לכדורעף להגיע לגובה המרבי שלו?
- מצא את הגובה המרבי של הכדורעף.
- תשובה
-
\(h=−16t^2+176t+4\)
מכיוון ש- a שלילי, הפרבולה נפתחת כלפי מטה.
למשוואה הריבועית יש מקסימום.
1.
\[\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}\]2.
מצא h כאשר t = 5.5. 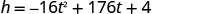
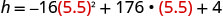
השתמש במחשבון כדי לפשט. 
הקודקוד הוא (5.5,488) מכיוון שלפרבולה יש מקסימום, קואורדינטת ה - h של הקודקוד היא ערך ה- y המרבי של המשוואה הריבועית. הערך המרבי של הריבוע הוא 488 רגל והוא מתרחש כאשר t = 5.5 שניות.
המשוואה הריבועית \(h=−16t^2+128t+32\) משמשת למציאת גובה אבן שנזרקת כלפי מעלה מגובה של 32 רגל בקצב של 128 רגל לשנייה. כמה זמן ייקח לאבן להגיע לגובה המרבי שלה? מהו הגובה המרבי? תשובות עגולות לעשירית הקרובה ביותר.
- תשובה
-
זה ייקח 4 שניות להגיע לגובה המרבי של 288 רגל.
רקטת צעצוע שנורתה כלפי מעלה מהקרקע בקצב של 208 רגל לשנייה כוללת את המשוואה הריבועית של. \(h=−16t^2+208t\) מתי תגיע הרקטה לגובהה המרבי? מה יהיה הגובה המרבי? תשובות עגולות לעשירית הקרובה ביותר.
- תשובה
-
ייקח 6.5 שניות להגיע לגובה המרבי של 676 רגל.
- גרפים פונקציות ריבועיות
- איך משרטטים פונקציה ריבועית?
- גרף משוואות ריבועיות
מושגי מפתח
- הגרף של כל משוואה ריבועית הוא פרבולה.
- כיוון פרבולה למשוואה \(y=ax^2+bx+c\) הריבועית, אם
- a> 0, הפרבולה נפתחת כלפי מעלה.
- a<0, הפרבולה נפתחת כלפי מטה.
- ציר סימטריה וקודקוד של פרבולה לפרבולה עם משוואה: \(y=ax^2+bx+c\)
- ציר הסימטריה של פרבולה הוא הקו\(x=−\frac{b}{2a}\).
- הקודקוד נמצא על ציר הסימטריה, כך שקואורדינטת ה - x שלו היא. \(−\frac{b}{2a}\)
- כדי למצוא את קואורדינטת y של הקודקוד אנו מחליפים \(x=−\frac{b}{2a}\) במשוואה הריבועית.
- מצא את יירוטים של פרבולה כדי למצוא את היירוט של פרבולה עם משוואה: \(y=ax^2+bx+c\)
\[\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}\] - לתרשים משוואה ריבועית בשני משתנים
- כתוב את המשוואה הריבועית עם yy בצד אחד.
- קבע אם הפרבולה נפתחת כלפי מעלה או מטה.
- מצא את ציר הסימטריה.
- מצא את הקודקוד.
- מצא את יירוט y. מצא את הנקודה סימטרית ליירוט y על פני ציר הסימטריה.
- מצא את ה - x -יירוט.
- גרף את הפרבולה.
- ערכי מינימום או מקסימום של משוואה ריבועית
- הקואורדינטה y של קודקוד הגרף של משוואה ריבועית היא
- ערך מינימלי של המשוואה הריבועית אם הפרבולה נפתחת כלפי מעלה.
- הערך המרבי של המשוואה הריבועית אם הפרבולה נפתחת כלפי מטה.
רשימת מילים
- ציר הסימטריה
- ציר הסימטריה הוא הקו האנכי העובר באמצע הפרבולה\(y=ax^2+bx+c\).
- פרבולה
- הגרף של משוואה ריבועית בשני משתנים הוא פרבולה.
- משוואה ריבועית בשני משתנים
- משוואה ריבועית בשני משתנים, כאשר a, b ו- c הם מספרים ממשיים \(a \ge 0\) והיא משוואה של הצורה\(y=ax^2+bx+c\).
- קודקוד
- הנקודה על הפרבולה שנמצאת על ציר הסימטריה נקראת קודקוד הפרבולה; זוהי הנקודה הנמוכה ביותר או הגבוהה ביותר בפרבולה, תלוי אם הפרבולה נפתחת כלפי מעלה או מטה.
- x -יירוט של פרבולה
- ה - x -יירוט הם הנקודות על הפרבולה היכן. \(y=0\)
- y -יירוט של פרבולה
- יירוט y הוא הנקודה על הפרבולה שבה. \(x=0\)


