פרק 10 תרגילי סקירה
- Page ID
- 205537
פרק 10 תרגילי סקירה
10.1 לפתור משוואות ריבועיות באמצעות מאפיין השורש הריבועי
בתרגילים הבאים, פתר באמצעות נכס השורש הריבועי.
\(x^2=100\)
- תשובה
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- תשובה
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- תשובה
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- תשובה
-
אין פתרון
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- תשובה
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- תשובה
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
בתרגילים הבאים, פתר באמצעות נכס השורש הריבועי.
\((p−5)^2+3=19\)
- תשובה
-
p=1, 9
\((q+4)^2=9\)
\((u+1)^2=45\)
- תשובה
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- תשובה
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- תשובה
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- תשובה
-
אין פתרון
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- תשובה
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- תשובה
-
א=−32, 34
\(4b^2−28b+49=25\)
10.2 לפתור משוואות ריבועיות באמצעות השלמת הריבוע
בתרגילים הבאים, השלם את הכיכר כדי ליצור טרינום מרובע מושלם. ואז כתוב את התוצאה כריבוע בינומי.
\(x^2+22x\)
- תשובה
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- תשובה
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- תשובה
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- תשובה
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
בתרגילים הבאים, לפתור על ידי השלמת הכיכר.
\(c^2+20c=21\)
- תשובה
-
ג=1, -21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- תשובה
-
איקס=−4, 8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- תשובה
-
אין פתרון
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- תשובה
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- תשובה
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- תשובה
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- תשובה
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- תשובה
-
p=0, 6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- תשובה
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- תשובה
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 לפתור משוואות ריבועיות באמצעות הנוסחה הריבועית
בתרגילים הבאים יש לפתור באמצעות הנוסחה הריבועית.
\(4x^2−5x+1=0\)
- תשובה
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- תשובה
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- תשובה
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- תשובה
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- תשובה
-
אין פתרון אמיתי
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- תשובה
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- תשובה
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- תשובה
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
בתרגילים הבאים, קבע את מספר הפתרונות לכל משוואה ריבועית.
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- תשובה
-
- 1
- 2
- 2
- אף אחד
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
בתרגילים הבאים, זהה את השיטה המתאימה ביותר (פקטורינג, שורש מרובע או פורמולה ריבועית) לשימוש כדי לפתור כל משוואה ריבועית.
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- תשובה
-
- גורם
- פורמולה ריבועית
- שורש ריבועי
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 לפתור יישומים לפי מודל משוואות ריבועיות
בתרגילים הבאים יש לפתור באמצעות שיטות פקטורינג, עקרון השורש הריבועי או הנוסחה הריבועית.
מצא שני מספרים אי-זוגיים רצופים שהמוצר שלהם הוא 323.
- תשובה
-
שני מספרים אי-זוגיים רצופים שהתוצר שלהם הוא 323 הם 17 ו -19, ו -17 ו -19.
מצא שני מספרים זוגיים רצופים שהמוצר שלהם הוא 624.
באנר משולש יש שטח של 351 סנטימטרים רבועים. אורך הבסיס הוא שני סנטימטרים יותר מפי ארבעה מהגובה. מצא את הגובה והאורך של הבסיס.
- תשובה
-
גובה הדגל הוא 13 ס"מ ואורך הצד 54 ס"מ.
יוליוס בנה ויטרינה משולשת לאוסף המטבעות שלו. גובה מארז התצוגה הוא שישה סנטימטרים פחות מכפליים מרוחב הבסיס. שטח החלק האחורי של המארז הוא 70 אינץ 'מרובע. מצא את הגובה והרוחב של המקרה.
פסיפס אריחים בצורת משולש ימני משמש כפינה של שביל מלבני. ההיפוטנוזה של הפסיפס היא 5 רגל. צד אחד של הפסיפס ארוך פי שניים מהצד השני. מהם אורכי הצדדים? סיבוב לעשירית הקרובה ביותר.

- תשובה
-
אורכי צידי הפסיפס הם 2.2 ו -4.4 רגל.
לפיסת דיקט מלבנית יש אלכסון המודד שני מטרים יותר מהרוחב. אורך הדיקט כפול מהרוחב. מה אורך האלכסון של הדיקט? סיבוב לעשירית הקרובה ביותר.
ההליכה הקדמית מהרחוב לביתו של פאם כוללת שטח של 250 מטרים רבועים. אורכו הוא פי שניים פחות מארבע פעמים רוחבו. מצא את אורך ורוחב המדרכה. סיבוב לעשירית הקרובה ביותר.
- תשובה
-
רוחב ההליכה הקדמית הוא 8.1 רגל ואורכו 30.8 רגל.
למסיבת הסיום של סופיה, כמה שולחנות באותו רוחב יסודרו מקצה לקצה כדי לתת שולחן הגשה בשטח כולל של 75 רגל מרובע. האורך הכולל של השולחנות יהיה פי שניים יותר משלושה מהרוחב. מצא את אורך ורוחב שולחן ההגשה כך שסופיה תוכל לרכוש את מפת השולחן בגודל הנכון. תשובה עגולה לעשירית הקרובה ביותר.
כדור נזרק אנכית באוויר במהירות של 160 רגל/שנייה. השתמש בנוסחה \(h=−16t^2+v_{0}t\) כדי לקבוע מתי הכדור יהיה 384 רגל מהקרקע. סיבוב לעשירית הקרובה ביותר.
- תשובה
-
הכדור יגיע ל 384 רגל בדרכו למעלה תוך 4 שניות ובדרך למטה תוך 6 שניות.
כדור נורה ישר מהקרקע במהירות של 320 רגל לשנייה. השתמש בנוסחה \(h=−16t^2+v_{0}t\) כדי לקבוע מתי הכדור יגיע 800 רגל. סיבוב לעשירית הקרובה ביותר.
10.5 גרף משוואות ריבועיות בשני משתנים
בתרגילים הבאים, גרף לפי נקודת התוויית.
גרף \(y=x^2−2\)
- תשובה
-
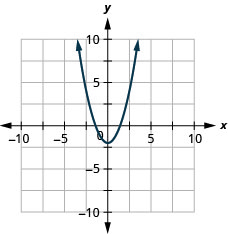
גרף \(y=−x^2+3\)
בתרגילים הבאים, קבע אם הפרבולות הבאות נפתחות למעלה או למטה.
\(y=−3x^2+3x−1\)
- תשובה
-
למטה
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- תשובה
-
למעלה
א \(y=−4x^2−7x+1\)
בתרגילים הבאים, מצא
- ציר הסימטריה,
- קודקוד.
\(y=−x^2+6x+8\)
- תשובה
-
- איקס=3
- (3,17)
\(y=2x^2−8x+1\)
בתרגילים הבאים, מצא את יירוט ה - x - ו - y.
\(y=x^2−4x+5\)
- תשובה
-
y: (0,5); איקס: (5,0), (−1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- תשובה
-
y: (0,10); x: אף אחד
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- תשובה
-
y: (0,1); איקס: (14,0)
\(y=x^2+16x+64\)
בתרגילים הבאים, גרף באמצעות יירוט, קודקוד וציר הסימטריה.
\(y=x^2+8x+15\)
- תשובה
-
y: (0,15); איקס: (-3,0), (-5,0);
ציר: x = -4; קודקוד :( -4, -1)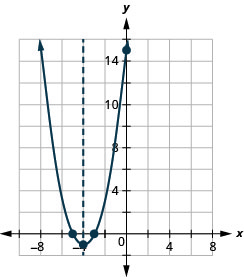
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- תשובה
-
y: (0, -16); x: (4,0);
ציר: x = 4; קודקוד: (4,0)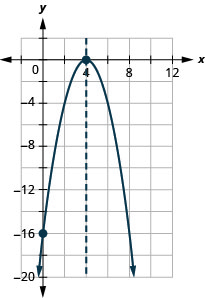
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- תשובה
-
y: (0,13); x: אף אחד;
ציר: x = -3; קודקוד :( -3,4)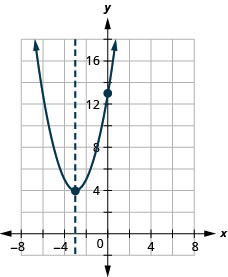
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- תשובה
-
y: (0, -11); x: (3.1,0), (0.9,0);
ציר: x = 2; קודקוד :( 2,5)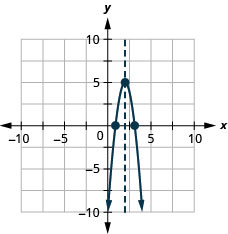
\(y=x^2+8x+10\)
בתרגילים הבאים, מצא את הערך המינימלי או המקסימלי.
\(y=7x^2+14x+6\)
- תשובה
-
הערך המינימלי הוא -1 כאשר\(x=−1\).
\(y=−3x^2+12x−10\)
בתרגילים הבאים, לפתור. עיגול תשובות לעשירית הקרובה ביותר.
כדור נזרק כלפי מעלה מהקרקע במהירות התחלתית של 112 רגל/שנייה. השתמש במשוואה הריבועית \(h=−16t^2+112t\) כדי למצוא כמה זמן ייקח לכדור להגיע לגובה המרבי ואז מצא את הגובה המרבי.
- תשובה
-
תוך 3.5 שניות הכדור נמצא בגובהו המרבי של 196 רגל.
מעון יום סוגר שטח מלבני בצד הבניין שלהם כדי שהילדים יוכלו לשחק בחוץ. הם צריכים למקסם את השטח באמצעות 180 רגל של גידור משלושה צידי החצר. המשוואה הריבועית \(A=−2x^2+180x\) נותנת את השטח, A, של החצר לאורך, x, של הבניין שיגבול בחצר. מצא את אורך הבניין שאמור לגבול את החצר כדי למקסם את השטח, ולאחר מכן מצא את השטח המרבי.
מבחן תרגול
השתמש במאפיין השורש הריבועי כדי לפתור את המשוואה הריבועית:\(3(w+5)^2=27\).
- תשובה
-
w=−2, −8
השתמש בהשלמת הריבוע כדי לפתור את המשוואה הריבועית: \(a^2−8a+7=23\)
השתמש בנוסחה הריבועית כדי לפתור את המשוואה הריבועית:. \(2m^2−5m+3=0\)
- תשובה
-
מ = 1, 32
לפתור את המשוואות הריבועיות הבאות. השתמש בכל שיטה.
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- תשובה
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- תשובה
-
אין פתרון אמיתי
\(\frac{4}{3}y^2−4y+3=0\)
השתמש במפלה כדי לקבוע את מספר הפתרונות של כל משוואה ריבועית.
\(6p^2−13p+7=0\)
- תשובה
-
2
\(3q^2−10q+12=0\)
פתור על ידי פקטורינג, נכס השורש הריבועי או הנוסחה הריבועית.
מצא שני מספרים זוגיים רצופים שהמוצר שלהם הוא 360.
- תשובה
-
שני מספרים זוגיים רצופים הם -20 ו -18 ו -18 ו -20.
אורכו של אלכסון של מלבן הוא שלושה יותר מהרוחב. אורך המלבן הוא פי שלושה מהרוחב. מצא את אורך האלכסון. (סיבוב לעשירית הקרובה ביותר.)
עבור כל פרבולה, מצא
- באילו דרכים הוא נפתח,
- ציר הסימטריה,
- קודקוד,
- ה - x - ו - y -מיירט, ו
- הערך המקסימלי או המינימלי.
\(y=3x^2+6x+8\)
- תשובה
-
- למעלה
- \(x=−1\)
- (-1,5)
- y: (0,8); x: אף אחד; y: (0,8)
- ערך מינימלי של 5 כאשר\(x=−1\).
\(y=x^2−4\)
\(y=x^2+10x+24\)
- תשובה
-
- למעלה
- \(x=−5\)
- (-5, -1)
- y: (0,24); איקס: (-6,0), (-4,0)
- ערך מינימלי של -5 כאשר \(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- תשובה
-
- מטה
- \(x=−4\)
- (-4,32)
- y; (0,16); איקס: (-9.7,0), (1.7,0)
- ערך מקסימלי של 32 כאשר \(x=−4\)
גרף את הפרבולות הבאות באמצעות יירוט, קודקוד וציר הסימטריה.
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- תשובה
-
y: (0,9); איקס: (-34,0)
ציר:; קודקוד: \( x=−\frac{3}{4}\) \((−\frac{3}{4},0)\)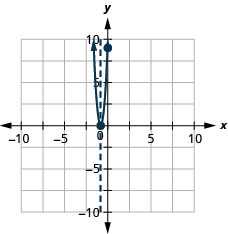
לפתור.
בלון מים משוגר כלפי מעלה בקצב של 86 רגל/שנייה. בעזרת הנוסחה h = −16t ^ 2+86t, מצא כמה זמן ייקח לבלון להגיע לגובה המרבי ואז מצא את הגובה המרבי. סיבוב לעשירית הקרובה ביותר.