6.5: מחלקים מונומיאלים

מטרות למידה

בסוף פרק זה, תוכל:

• פשט ביטויים באמצעות המאפיין Quotient עבור מעריכים
• פשט ביטויים עם אפס אקספוננטים
• פשט ביטויים באמצעות המנה למאפיין כוח
• פשט ביטויים על ידי החלת מספר מאפיינים
• מחלקים מונומיאלים

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

1. פשט:\(\dfrac{8}{24}\).
   אם פספסת בעיה זו, עיין בתרגיל 1.6.4.
2. פשט:\((2m^3)^5\).
   אם פספסת בעיה זו, עיין בתרגיל 6.2.22.
3. פשט: \(\dfrac{12x}{12y}\)
   אם פספסת בעיה זו, עיין בתרגיל 1.6.10.

פשט ביטויים באמצעות המאפיין Quotient עבור מעריכים

מוקדם יותר בפרק זה פיתחנו את המאפיינים של אקספונסנטים לכפל. אנו מסכמים מאפיינים אלה להלן.

סיכום תכונות אקספוננט לכפל

אם a ו- b הם מספרים ממשיים, ו- m ו- n הם מספרים שלמים, אז

\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]

כעת נבחן את המאפיינים המעריכים לחלוקה. רענון זיכרון מהיר עשוי לעזור לפני שנתחיל. למדת לפשט שברים על ידי חלוקת גורמים משותפים מהמונה והמכנה באמצעות המאפיין שברים שווים. מאפיין זה גם יעזור לך לעבוד עם שברים אלגבריים - שהם גם מנות.

נכס שברים שווה ערך

אם a, b ו- c הם מספרים שלמים היכן\(b\neq 0,c\neq 0\).

\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]

כמו בעבר, ננסה לגלות נכס על ידי הסתכלות על כמה דוגמאות.

\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]

שימו לב, בכל מקרה הבסיסים היו זהים וחיסרנו אקספונסנטים.

כאשר המעריך הגדול יותר היה במונה, נותרנו עם גורמים במונה.

כאשר המעריך הגדול יותר היה במכנה, נותרנו עם גורמים במכנה - שימו לב למונה של 1.

אנו כותבים:

\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]

זה מוביל לנכס המנה עבור מעריכים.

נכס מנה למעריכים

אם a הוא מספר ממשי\(a\neq 0\), ו- m ו- n הם מספרים שלמים, אז

\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]

כמה דוגמאות עם מספרים עשויות לעזור לאמת נכס זה.

\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]

תרגיל \(\PageIndex{1}\)

פשט:

1. \(\dfrac{x^{9}}{x^{7}}\)
2. \(\dfrac{3^{10}}{3^{2}}\)

תשובה

כדי לפשט ביטוי עם מנה, עלינו להשוות תחילה את המעריכים במונה ובמכנה.

1.

מאז 9 > 7, ישנם גורמים נוספים של x במונה.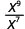
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=a^{m-n}\)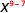
לפשט.	\(x^2\)

2.

מאז 10> 2, ישנם גורמים נוספים של x במונה.
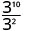
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=a^{m-n}\)
לפשט.	\(3^8\)

שימו לב שכאשר המעריך הגדול יותר נמצא במונה, נותרנו עם גורמים במונה.

תרגיל \(\PageIndex{2}\)

פשט:

1. \(\dfrac{x^{15}}{x^{10}}\)
2. \(\dfrac{6^{14}}{6^{5}}\)

תשובה

1. \(x^{5}\)
2. \(6^9\)

תרגיל \(\PageIndex{3}\)

פשט:

1. \(\dfrac{y^{43}}{y^{37}}\)
2. \(\dfrac{10^{15}}{10^{7}}\)

תשובה

1. \(y^{6}\)
2. \(10^8\)

תרגיל \(\PageIndex{4}\)

פשט:

1. \(\dfrac{b^{8}}{b^{12}}\)
2. \(\dfrac{7^{3}}{7^{5}}\)

תשובה

כדי לפשט ביטוי עם מנה, עלינו להשוות תחילה את המעריכים במונה ובמכנה.

1.

מאז 12> 8, ישנם גורמים נוספים של b במכנה.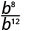
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)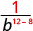
לפשט.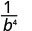

2.

מאז 5> 3, ישנם גורמים נוספים של 3 במכנה.
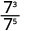
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)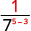
לפשט.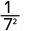
לפשט.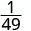

שימו לב שכאשר המעריך הגדול יותר נמצא במכנה, נותרנו עם גורמים במכנה.

תרגיל \(\PageIndex{5}\)

פשט:

1. \(\dfrac{x^{18}}{x^{22}}\)
2. \(\dfrac{12^{15}}{12^{30}}\)

תשובה

1. \(\dfrac{1}{x^{4}}\)
2. \(\dfrac{1}{12^{15}}\)

תרגיל \(\PageIndex{6}\)

פשט:

1. \(\dfrac{m^{7}}{m^{15}}\)
2. \(\dfrac{9^{8}}{9^{19}}\)

תשובה

1. \(\dfrac{1}{m^{8}}\)
2. \(\dfrac{1}{9^{11}}\)

שימו לב להבדל בשתי הדוגמאות הקודמות:

• אם נתחיל עם גורמים נוספים במונה, נסיים עם גורמים במונה.
• אם נתחיל עם גורמים נוספים במכנה, נסיים עם גורמים במכנה.

השלב הראשון בפישוט ביטוי באמצעות המאפיין Quotient עבור אקספוננטים הוא לקבוע אם המעריך גדול יותר במונה או במכנה.

תרגיל \(\PageIndex{7}\)

פשט:

1. \(\dfrac{a^{5}}{a^{9}}\)
2. \(\dfrac{x^{11}}{x^{7}}\)

תשובה

1. האם המעריך של גדול יותר במונה או במכנה? מאז 9 > 5, יש יותר a במכנה ולכן בסופו של דבר נקבל גורמים במכנה.

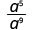
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)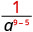
לפשט.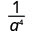

2. שימו לב שיש יותר גורמים של xx במונה, מאז 11> 7. אז נסיים עם גורמים במונה.

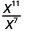
השתמש במאפיין המנה, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\)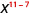
לפשט.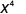

תרגיל \(\PageIndex{8}\)

פשט:

1. \(\dfrac{b^{19}}{b^{11}}\)
2. \(\dfrac{z^{5}}{z^{11}}\)

תשובה

1. \(b^{8}\)
2. \(\dfrac{1}{z^{6}}\)

תרגיל \(\PageIndex{9}\)

פשט:

1. \(\dfrac{p^{9}}{p^{17}}\)
2. \(\dfrac{w^{13}}{w^{9}}\)

תשובה

1. \(\dfrac{1}{p^{8}}\)
2. \(w^{4}\)

פשט ביטויים עם אקספוננט של אפס

מקרה מיוחד של המאפיין Quotient הוא כאשר המעריכים של המונה והמכנה שווים, כגון ביטוי כמו. \(\dfrac{a^{m}}{a^{m}}\) מהעבודה הקודמת שלך עם שברים, אתה יודע ש:

\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]

במילים, מספר המחולק בפני עצמו הוא 1. אז,\(\dfrac{x}{x}=1\), עבור כל\(x(x\neq 0)\), שכן כל מספר מחולק בפני עצמו הוא 1.

המאפיין Quotient עבור Exponents מראה לנו כיצד לפשט \(\dfrac{a^{m}}{a^{n}}\) מתי \(m>n\) ומתי על \(n<m\) ידי חיסור אקספונסנטים. מה אם\(m=n\)?

שקול\(\dfrac{8}{8}\), אשר אנו יודעים הוא 1.

\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)

כעת נפשט \(\dfrac{a^{m}}{a^{m}}\) בשתי דרכים להוביל אותנו להגדרת מעריך האפס. באופן כללי, עבור\(a\neq 0\):

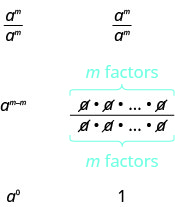
אנו רואים \(\dfrac{a^{m}}{a^{m}}\) מפשט \(a^{0}\) ל -1. אז\(a^{0} = 1\).

אפס אקספקטנט

אם a הוא מספר שאינו אפס, אז\(a^{0} = 1\).

כל מספר שאינו אפס שהועלה לכוח האפס הוא 1.

בטקסט זה אנו מניחים שכל משתנה שאנו מעלים לכוח האפס אינו אפס.

תרגיל \(\PageIndex{10}\)

פשט:

1. \(9^{0}\)
2. \(n^{0}\)

תשובה

ההגדרה אומרת שכל מספר שאינו אפס שהועלה לכוח האפס הוא 1.

1. \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
2. \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)

תרגיל \(\PageIndex{11}\)

פשט:

1. \(15^{0}\)
2. \(m^{0}\)

תשובה

1. 1
2. 1

תרגיל \(\PageIndex{12}\)

פשט:

1. \(k^{0}\)
2. \(29^{0}\)

תשובה

1. 1
2. 1

כעת, לאחר שהגדרנו את מעריך האפס, נוכל להרחיב את כל המאפיינים של אקספוננטים כך שיכללו מעריכי מספרים שלמים.

מה לגבי העלאת ביטוי לכוח האפס? בואו נסתכל על\((2x)^0\). אנו יכולים להשתמש במוצר לכלל כוח לשכתב ביטוי זה.

\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]

זה אומר לנו שכל ביטוי שאינו אפס המועלה לכוח האפס הוא אחד.

תרגיל \(\PageIndex{13}\)

פשט:

1. \((5b)^0\)
2. \((−4a^{2}b)^0\).

תשובה

1. \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
2. \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)

תרגיל \(\PageIndex{14}\)

פשט:

1. \((11z)^0\)
2. \((−11pq^{3})^0\).

תשובה

1. 1
2. 1

תרגיל \(\PageIndex{15}\)

פשט:

1. \((-6d)^0\)
2. \((−8m^{2}n^{3})^0\).

תשובה

1. 1
2. 1

פשט ביטויים באמצעות המנה לנכס כוח

כעת נבחן דוגמה שתוביל אותנו למניין לנכס כוח.

\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]

שימו לב שהמעריך חל הן על המונה והן על המכנה.

\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]

זה מוביל למנה לנכס כוח עבור מעריכים.

מנה לנכס כוח עבור אקספונסנטים

אם a ו- b הם מספרים ממשיים\(b\neq 0\), ו- m הוא מספר ספירה, אז

\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]

כדי להעלות שבריר לכוח, הרם את המונה והמכנה לכוח זה.

דוגמה עם מספרים עשויה לעזור לך להבין מאפיין זה:

\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]

תרגיל \(\PageIndex{16}\)

פשט:

1. \(\left(\dfrac{3}{7}\right)^{2}\)
2. \(\left(\dfrac{b}{3}\right)^{4}\)
3. \(\left(\dfrac{k}{j}\right)^{3}\)

תשובה

1.

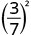
השתמש במאפיין המנה, \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)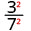
לפשט.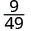

2.

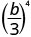
השתמש במאפיין המנה, \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)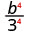
לפשט.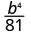

3.

הרם את המונה והמכנה לכוח השלישי.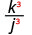

תרגיל \(\PageIndex{17}\)

פשט:

1. \(\left(\dfrac{5}{8}\right)^{2}\)
2. \(\left(\dfrac{p}{10}\right)^{4}\)
3. \(\left(\dfrac{m}{n}\right)^{7}\)

תשובה

1. \(\dfrac{25}{64}\)
2. \(\dfrac{p^{4}}{10,000}\)
3. \(\dfrac{m^{7}}{n^{7}}\)

תרגיל \(\PageIndex{18}\)

פשט:

1. \(\left(\dfrac{1}{3}\right)^{3}\)
2. \(\left(\dfrac{-2}{q}\right)^{3}\)
3. \(\left(\dfrac{w}{x}\right)^{4}\)

תשובה

1. \(\dfrac{1}{27}\)
2. \(\dfrac{-8}{q^{3}}\)
3. \(\dfrac{w^{4}}{x^{4}}\)

פשט ביטויים על ידי החלת מספר מאפיינים

כעת נסכם את כל המאפיינים של אקספונסנטים כך שכולם יחד להתייחס אליהם כאשר אנו מפשטים ביטויים באמצעות מספר מאפיינים. שימו לב שהם מוגדרים כעת עבור מעריכי מספרים שלמים.

סיכום של מאפייני אקספוננט

אם a ו- b הם מספרים ממשיים, ו- m ו- n הם מספרים שלמים, אז

\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]

תרגיל \(\PageIndex{19}\)

פשט: \(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)

תשובה

\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)

תרגיל \(\PageIndex{20}\)

פשט: \(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)

תשובה

\(m^{13}\)

תרגיל \(\PageIndex{21}\)

פשט: \(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)

תשובה

\(k^{5}\)

תרגיל \(\PageIndex{22}\)

פשט: \(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)

תשובה

\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]

שימו לב שאחרי שפשטנו את המכנה בשלב הראשון, המונה והמכנה היו שווים. אז הערך הסופי שווה ל 1.

תרגיל \(\PageIndex{23}\)

לפשט\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).

תשובה

1

תרגיל \(\PageIndex{24}\)

לפשט\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).

תשובה

1

תרגיל \(\PageIndex{25}\)

פשט: \(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)

תשובה

\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]

תרגיל \(\PageIndex{25}\)

פשט: \(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)

תשובה

\(r^{8}\)

תרגיל \(\PageIndex{25}\)

פשט: \(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)

תשובה

\(v^{6}\)

תרגיל \(\PageIndex{26}\)

פשט: \(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)

תשובה

כאן איננו יכולים לפשט תחילה בתוך הסוגריים, מכיוון שהבסיסים אינם זהים.

\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)

תרגיל \(\PageIndex{27}\)

פשט: \(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)

תשובה

\(\dfrac{a^{12}}{b^{8}}\)

תרגיל \(\PageIndex{28}\)

פשט: \(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)

תשובה

\(\dfrac{q^{21}}{r^{15}}\)

תרגיל \(\PageIndex{29}\)

פשט: \(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)

תשובה

\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)

תרגיל \(\PageIndex{30}\)

פשט: \(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)

תשובה

\(\dfrac{49 x^{6}}{81 y^{2}}\)

תרגיל \(\PageIndex{31}\)

פשט: \(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)

תשובה

\(\dfrac{9 x^{8}}{49 v^{2}}\)

תרגיל \(\PageIndex{32}\)

פשט: \(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)

תשובה

\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)

תרגיל \(\PageIndex{32}\)

פשט: \(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)

תשובה

\(\dfrac{1}{a^{6}}\)

תרגיל \(\PageIndex{33}\)

פשט: \(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)

תשובה

\(\dfrac{1}{p^{15}}\)

תרגיל \(\PageIndex{34}\)

פשט: \(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)

תשובה

\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)

תרגיל \(\PageIndex{35}\)

פשט: \(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)

תשובה

9 \(r^{18}\)

תרגיל \(\PageIndex{36}\)

פשט: \(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)

תשובה

\(\dfrac{2}{x}\)

מחלקים מונומיאלים

כעת התוודעתם לכל המאפיינים של אקספונסנטים והשתמשתם בהם כדי לפשט ביטויים. לאחר מכן, תראה כיצד להשתמש במאפיינים אלה כדי לחלק מונומיאלים. מאוחר יותר, תשתמש בהם כדי לחלק פולינומים.

תרגיל \(\PageIndex{37}\)

מצא את המנה: \(56 x^{7} \div 8 x^{3}\)

תשובה

\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]

תרגיל \(\PageIndex{38}\)

מצא את המנה: \(42y^{9} \div 6 y^{3}\)

תשובה

\(7y^{6}\)

תרגיל \(\PageIndex{39}\)

מצא את המנה: \(48z^{8} \div 8 z^{2}\)

תשובה

\(6z^{6}\)

תרגיל \(\PageIndex{40}\)

מצא את המנה: \(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)

תשובה

כאשר אנו מחלקים מונומיאלים עם יותר ממשתנה אחד, אנו כותבים שבר אחד לכל משתנה.

\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)

תרגיל \(\PageIndex{41}\)

מצא את המנה: \(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)

תשובה

\(-\dfrac{9}{a^{5} b}\)

תרגיל \(\PageIndex{42}\)

מצא את המנה: \(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)

תשובה

\(\dfrac{-9 d}{c^{4}}\)

תרגיל \(\PageIndex{43}\)

מצא את המנה: \(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)

תשובה

\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)

תרגיל \(\PageIndex{44}\)

מצא את המנה: \(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)

תשובה

\(\dfrac{2 a^{6}}{3 b^{2}}\)

תרגיל \(\PageIndex{45}\)

מצא את המנה: \(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)

תשובה

\(-\dfrac{3 q^{6}}{5 p^{8}}\)

לאחר שתכיר את התהליך ותרגל אותו צעד אחר צעד מספר פעמים, ייתכן שתוכל לפשט שבריר בצעד אחד.

תרגיל \(\PageIndex{46}\)

מצא את המנה: \(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)

תשובה

היזהר מאוד לפשט \(\dfrac{14}{21}\) על ידי חלוקת גורם משותף, ולפשט את המשתנים על ידי חיסור המעריכים שלהם.

\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)

תרגיל \(\PageIndex{47}\)

מצא את המנה: \(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)

תשובה

\(\dfrac{4 y^{2}}{7 x^{4}}\)

תרגיל \(\PageIndex{48}\)

מצא את המנה: \(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)

תשובה

\(\dfrac{5}{8 m^{5} n^{3}}\)

בכל הדוגמאות עד כה, לא הייתה שום עבודה במונה או במכנה לפני שפשטו את השבר. בדוגמה הבאה, נמצא תחילה את התוצר של שני מונומיאלים במונה לפני שנפשט את השבר. זה בעקבות סדר הפעולות. זכור, סרגל שברים הוא סמל קיבוץ.

תרגיל \(\PageIndex{49}\)

מצא את המנה: \(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)

תשובה

\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)

תרגיל \(\PageIndex{50}\)

מצא את המנה: \(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)

תשובה

\(2 a b^{2}\)

תרגיל \(\PageIndex{51}\)

מצא את המנה: \(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)

תשובה

\(-4 x y^{5}\)

הערה

גש למשאבים מקוונים אלה להדרכה ותרגול נוספים עם מונומיאלים חלוקים:

• ביטויים רציונליים
• חלוקת מונומיאלים
• חלוקת מונומיאלים 2

מושגי מפתח

• נכס מנה למעריכים:
  • אם a הוא מספר ממשי\(a\neq 0\), ו- m, n הם מספרים שלמים, אז: \(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
• אפס אקספוננט
  • אם a הוא מספר שאינו אפס, אז\(a^{0} =1\).
• מנה לנכס כוח עבור מעריכים:
  • אם a ו- b הם מספרים ממשיים\(b\neq 0\), ו- mm הוא מספר ספירה, אז: \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
  • כדי להעלות שבריר לכוח, הרם את המונה והמכנה לכוח זה.
• סיכום מאפייני אקספוננט
  • אם a, b הם מספרים ממשיים ו- m, nm, n הם מספרים שלמים, אז \(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)