6.4: מוצרים מיוחדים
- Page ID
- 205576
בסוף פרק זה תוכל:
- ריבוע בינומי באמצעות תבנית הריבועים הבינומיים
- הכפל מצומדים באמצעות המוצר של תבנית מצומדים
- הכירו את תבנית המוצר המיוחדת המתאימה והשתמשו בה
לפני שתתחיל, קח את חידון המוכנות הזה.
פשט: א. \(9^2\) ב. \((−9)^2\) ג\(−9^2\).
אם פספסת בעיה זו, סקור את תרגיל 1.5.13.
ריבוע בינומי באמצעות תבנית הריבועים הבינומיים
מתמטיקאים אוהבים לחפש דפוסים שיקלו על עבודתם. דוגמה טובה לכך היא בינומים בריבוע. אמנם אתה תמיד יכול להשיג את המוצר על ידי כתיבת הבינום פעמיים ושימוש בשיטות של החלק האחרון, אך יש פחות עבודה לעשות אם אתה לומד להשתמש בתבנית.
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
תסתכל על התוצאות האלה. האם אתה רואה דפוסים כלשהם?
מה לגבי מספר המונחים? בכל דוגמה ריבענו בינומיום והתוצאה הייתה טרינום.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
עכשיו תסתכל על המונח הראשון בכל תוצאה. מאיפה זה בא?
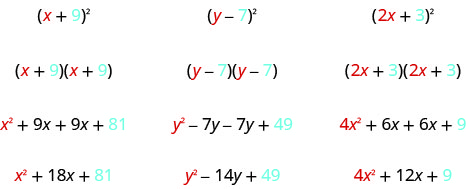
המונח הראשון הוא תוצר של המונחים הראשונים של כל בינומי. מכיוון שהבינומים זהים, זה רק הריבוע של הקדנציה הראשונה!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
כדי לקבל את המונח הראשון של המוצר, מרובע את המונח הראשון.
מאיפה הגיע המונח האחרון? התבונן בדוגמאות ומצא את התבנית.
המונח האחרון הוא תוצר של המונחים האחרונים, שהוא הריבוע של המונח האחרון.
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
כדי לקבל את המונח האחרון של המוצר, מרובע את המונח האחרון.
לבסוף, תסתכל על טווח הביניים. שימו לב שזה בא מהוספת המונחים "החיצוניים" וה"פנימיים" - ששניהם זהים! אז המונח האמצעי הוא כפול מהתוצר של שני המונחים של הבינום.
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
כדי לקבל את טווח הביניים של המוצר, להכפיל את התנאים להכפיל את המוצר שלהם.
לשים את כל זה ביחד:
אם \(a\) \(b\) והם מספרים ממשיים, התבנית הריבועית הבינומית היא
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
החלת זה על שני סוגים בינומיים:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
לריבוע בינומי:
- מרובע את המונח הראשון
- מרובע את המונח האחרון
- להכפיל את המוצר
דוגמה למספר עוזרת לאמת את התבנית.
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
כדי להכפיל \((10+4)^2\) בדרך כלל היית עוקב אחר סדר הפעולות.
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
התבנית עובדת!
\(\text { Multiply: }(x+5)^{2}\)
פתרון:
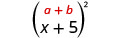 |
|
| מרובע את המונח הראשון. |  |
| מרובע את הקדנציה האחרונה. |  |
| הכפיל את המוצר. |  |
| לפשט. | \(x^{2}+10 x+25\) |
הכפל: \((x+9)^{2}\)
- תשובה
-
\(x^{2}+18 x+81\)
הכפל: \((y+11)^{2}\)
- תשובה
-
\(y^{2}+22 y+121\)
הכפל: \((y-3)^{2}\)
פתרון:
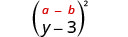 |
|
| מרובע את המונח הראשון. |  |
| מרובע את הקדנציה האחרונה. |  |
| הכפיל את המוצר. | 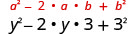 |
| לפשט. | \(y^{2}-6 y+9\) |
הכפל: \((x-9)^{2}\)
- תשובה
-
\(x^{2}-18 x+81\)
הכפל: \((p-13)^{2}\)
- תשובה
-
\(p^{2}-26 p+169\)
הכפל: \((4 x+6)^{2}\)
פתרון:
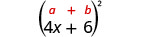 |
|
| השתמש בתבנית. | 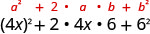 |
| לפשט. | \(16 x^{2}+48 x+36\) |
הכפל: \((6 x+3)^{2}\)
- תשובה
-
\(36 x^{2}+36 x+9\)
הכפל: \((4 x+9)^{2}\)
- תשובה
-
\(16 x^{2}+72 x+81\)
הכפל: \((2 x-3 y)^{2}\)
פתרון:
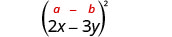 |
|
| השתמש בתבנית. | 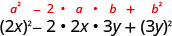 |
| לפשט. | \(4 x^{2}-12 x y+9 y^{2}\) |
הכפל: \((2 c-d)^{2}\)
- תשובה
-
\(4 c^{2}-4 c d+d^{2}\)
הכפל: \((4 x-5 y)^{2}\)
- תשובה
-
\(16 x^{2}-40 x y+25 y^{2}\)
הכפל: \(\left(4 u^{3}+1\right)^{2}\)
פתרון:
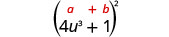 |
|
| השתמש בתבנית. | 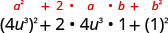 |
| לפשט. | \(16 u^{6}+8 u^{3}+1\) |
הכפל: \(\left(2 x^{2}+1\right)^{2}\)
- תשובה
-
\(4 x^{4}+4 x^{2}+1\)
הכפל: \(\left(3 y^{3}+2\right)^{2}\)
- תשובה
-
\(9 y^{6}+12 y^{3}+4\)
הכפל מצומדים באמצעות תוצר של תבנית מצומדים
בדיוק ראינו דפוס לריבוע בינומים שנוכל להשתמש בו כדי להקל על הכפלת כמה בינומים. באופן דומה, יש דפוס למוצר אחר של בינומים. אבל לפני שנגיע לזה, אנחנו צריכים להציג כמה אוצר מילים.
מה אתה מבחין בזוגות הבינומים האלה?
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
תסתכל על המונח הראשון של כל בינומי בכל זוג.
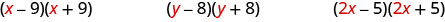
שימו לב שהמונחים הראשונים זהים בכל זוג.
תסתכל על המונחים האחרונים של כל בינומי בכל זוג.
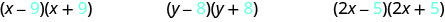
שימו לב שהמונחים האחרונים זהים בכל זוג.
שימו לב כיצד לכל זוג יש סכום אחד והבדל אחד.
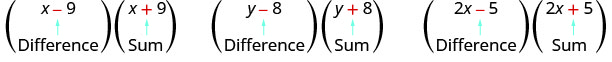
זוג בינומים שלכל אחד מהם אותו מונח ראשון ואותו מונח אחרון, אך אחד הוא סכום ואחד הוא הבדל יש שם מיוחד. זה נקרא זוג מצומד והוא מהצורה (a−b), (a+b).
זוג מצומד הוא שני בינומים של הצורה
\[(a-b),(a+b)\nonumber \]
לזוג הבינומים כל אחד יש אותו מונח ראשון ואותו מונח אחרון, אך בינומי אחד הוא סכום והשני הוא הבדל.
יש דפוס נחמד למציאת תוצר של מצמידים. אתה יכול, כמובן, פשוט FOIL כדי להשיג את המוצר, אך השימוש בתבנית מקל על העבודה שלך.
בואו נחפש את התבנית על ידי שימוש ב- FOIL כדי להכפיל כמה זוגות מצומדים.
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
כל מונח ראשון הוא תוצר של המונחים הראשונים של הבינומים, ומכיוון שהם זהים זהו הריבוע של המונח הראשון.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
המונח האחרון הגיע מכפלת המונחים האחרונים, הריבוע של הקדנציה האחרונה.
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
מה אתה רואה לגבי המוצרים?
התוצר של שני הבינומים הוא גם בינומי! רוב המוצרים הנובעים מ- FOIL היו טרינומים.
למה אין טווח ביניים? שימו לב לשני המונחים האמצעיים שאתם מקבלים מ-FOIL משלבים ל-0 בכל מקרה, תוצאה של תוספת אחת וחיסור אחד.
תוצר של מצומדים הוא תמיד מהצורה\(a^2-b^2\). זה נקרא הבדל של ריבועים.
זה מוביל לדפוס:
אם \(a\) \(b\) ומספרים אמיתיים,

המוצר נקרא הבדל של ריבועים.
כדי להכפיל מצומדים, מרובע את המונח הראשון, מרובע את המונח האחרון, ולכתוב את המוצר כהבדל של ריבועים.
בואו נבדוק דפוס זה בעזרת דוגמה מספרית.
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
שימו לב, התוצאה זהה!
הכפל: \((x-8)(x+8)\)
פתרון:
ראשית, הכירו בכך כתוצר של מצמידים. לבינומים יש אותם מונחים ראשונים, ואותם מונחים אחרונים, ובינומי אחד הוא סכום והשני הוא הבדל.
| זה מתאים לדפוס. | 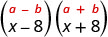 |
| ריבוע המונח הראשון, x. | 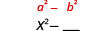 |
| ריבוע הקדנציה האחרונה, 8. | 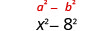 |
| המוצר הוא הבדל של ריבועים. | 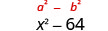 |
הכפל: \((x-5)(x+5)\)
- תשובה
-
\(x^{2}-25\)
הכפל: \((w-3)(w+3)\)
- תשובה
-
\(w^{2}-9\)
הכפל: \((2 x+5)(2 x-5)\)
פתרון:
האם הבינומים מצומדים?
| זהו תוצר של מצמידים. | 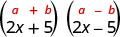 |
| ריבוע המונח הראשון, 2 x. | 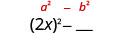 |
| ריבוע הקדנציה האחרונה, 5. | 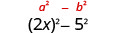 |
| לפשט. המוצר הוא הבדל של ריבועים. | 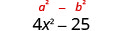 |
הכפל: \((6 x+5)(6 x-5)\)
- תשובה
-
\(36 x^{2}-25\)
הכפל: \((2 x+7)(2 x-7)\)
- תשובה
-
\(4 x^{2}-49\)
הבינומים בדוגמה הבאה עשויים להסתכל אחורה - המשתנה נמצא בקדנציה השנייה. אבל שני הבינומים עדיין מצומדים, ולכן אנו משתמשים באותה תבנית כדי להכפיל אותם.
מצא את המוצר: \((3+5 x)(3-5 x)\)
פתרון:
| זהו תוצר של מצמידים. | 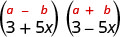 |
| השתמש בתבנית. | 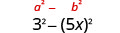 |
| לפשט. | \(9-25 x^{2}\) |
הכפל: \((7+4 x)(7-4 x)\)
- תשובה
-
\(49-16 x^{2}\)
הכפל: \((9-2 y)(9+2 y)\)
- תשובה
-
\(81-4 y^{2}\)
כעת נכפיל מצומדים שיש להם שני משתנים.
מצא את המוצר: \((5 m-9 n)(5 m+9 n)\)
פתרון:
| זה מתאים לדפוס. | 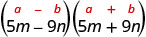 |
| השתמש בתבנית. | 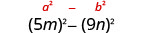 |
| לפשט. | \(25 m^{2}-81 n^{2}\) |
מצא את המוצר: \((4 p-7 q)(4 p+7 q)\)
- תשובה
-
\(16 p^{2}-49 q^{2}\)
מצא את המוצר: \((3 x-y)(3 x+y)\)
- תשובה
-
\(9 x^{2}-y^{2}\)
מצא את המוצר: \((c d-8)(c d+8)\)
פתרון:
| זה מתאים לדפוס. | 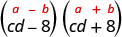 |
| השתמש בתבנית. | 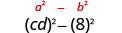 |
| לפשט. | \(c^{2} d^{2}-64\) |
מצא את המוצר: \((x y-6)(x y+6)\)
- תשובה
-
\(x^{2} y^{2}-36\)
מצא את המוצר: \((a b-9)(a b+9)\)
- תשובה
-
\(a^{2} b^{2}-81\)
מצא את המוצר: \(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
פתרון:
| זה מתאים לדפוס. | 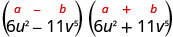 |
| השתמש בתבנית. | 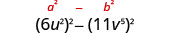 |
| לפשט. | \(36 u^{4}-121 v^{10}\) |
מצא את המוצר: \(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- תשובה
-
\(9 x^{4}-16 y^{6}\)
מצא את המוצר: \(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- תשובה
-
\(4 m^{4}-25 n^{6}\)
הכירו והשתמשו בתבנית המוצר המיוחדת המתאימה
זה עתה פיתחנו דפוסי מוצר מיוחדים לריבועים בינומיים ולמוצר של מצומדים. המוצרים נראים דומים, ולכן חשוב להכיר מתי ראוי להשתמש בכל אחד מהדפוסים הללו ולהבחין במה הם שונים. הסתכלו על שני הדפוסים יחד ושימו לב לדמיון ולהבדלים ביניהם.
\(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)
בחר את התבנית המתאימה והשתמש בה כדי למצוא את המוצר:
- \((2 x-3)(2 x+3)\)
- \((8 x-5)^{2}\)
- \((6 m+7)^{2}\)
- \((5 x-6)(6 x+5)\)
פתרון:
1. \((2x−3)(2x+3)\)אלה מצומדים. יש להם אותם מספרים ראשונים, ואותם מספרים אחרונים, ובינומי אחד הוא סכום והשני הוא הבדל. זה מתאים למוצר של דפוס מצומדים.
| זה מתאים לדפוס. | 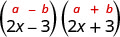 |
| השתמש בתבנית. | 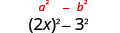 |
| לפשט. | \(4 x^{2}-9\) |
2. \((8 x-5)^{2}\)אנו מתבקשים לרבוע בינומי. זה מתאים לתבנית הריבועים הבינומיים.
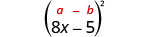 |
|
| השתמש בתבנית. |  |
| לפשט. | \(64 x^{2}-80 x+25\) |
3. \((6 m+7)^{2}\)שוב, אנו מרובעים בינומיום ולכן נשתמש בתבנית הריבועים הבינומיים.
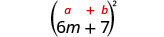 |
|
| השתמש בתבנית. |  |
| לפשט. | \(36 m^{2}+84 m+49\) |
4. \((5 x-6)(6 x+5)\)מוצר זה אינו מתאים לדפוסים, לכן נשתמש ב- FOIL.
\(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)
בחר את התבנית המתאימה והשתמש בה כדי למצוא את המוצר:
- \((9b−2)(2b+9)\)
- \((9p−4)2\)
- \((7y+1)^2\)
- \((4r-3)(4r+3)\)
- תשובה
-
- רדיד; \(18 b^{2}+77 b-18\)
- ריבועים בינומיים; \(81 p^{2}-72 p+16\)
- ריבועים בינומיים; \(49 y^{2}+14 y+1\)
- תוצר של מצומדים; \(16 r^{2}-9\)
בחר את התבנית המתאימה והשתמש בה כדי למצוא את המוצר:
- \((6x+7)^2\)
- \((3x−4)(3x+4)\)
- \((2x−5)(5x−2)\)
- \((6n−1)^2\)
- תשובה
-
- ריבועים בינומיים; \(36 x^{2}+84 x+49\)
- תוצר של מצומדים; \(9 x^{2}-16\)
- רדיד; \(10 x^{2}-29 x+10\)
- ריבועים בינומיים; \(36 n^{2}-12 n+1\)
גש למשאבים מקוונים אלה לקבלת הדרכה ותרגול נוספים עם מוצרים מיוחדים:
- מוצרים מיוחדים
מושגי מפתח
- תבנית ריבועים בינומיים
- אם a, b הם מספרים ממשיים,
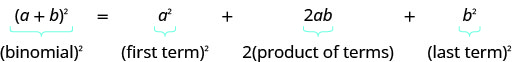
- \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
- \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
- לריבוע בינומי: מרובע את המונח הראשון, מרובע את המונח האחרון, הכפיל את המוצר שלהם.
- אם a, b הם מספרים ממשיים,
- תוצר של דפוס מצומדים
- אם a, ba, b הם מספרים ממשיים,
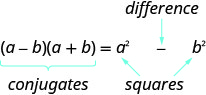
- \((a-b)(a+b)=a^{2}-b^{2}\)
- המוצר נקרא הבדל של ריבועים.
- אם a, ba, b הם מספרים ממשיים,
- כדי להכפיל מצומדים:
- ריבוע המונח הראשון ריבוע המונח האחרון כתוב אותו כהבדל של ריבועים
רשימת מילים
- זוג מצומד
- זוג מצומד הוא שני בינומים מהצורה \((a−b)\) ו\((a+b)\); לזוג הבינומים לכל אחד יש אותו מונח ראשון ואותו מונח אחרון, אך בינומי אחד הוא סכום והשני הוא הבדל.


