4.6E: תרגילים
- Page ID
- 205774
תרגול הופך למושלם
מצא משוואה של הקו בהינתן המדרון ו \(y\) - יירוט
בתרגילים הבאים, מצא את המשוואה של קו עם שיפוע נתון ו \(y\) -יירוט. כתוב את המשוואה בצורת שיפוע — יירוט.
שיפוע \(3\) ו \(y\) -יירוט \((0,5)\)
שיפוע \(4\) ו \(y\) -יירוט \((0,1)\)
- תשובה
-
\(y=4x+1\)
שיפוע \(6\) ו \(y\) -יירוט \((0,−4)\)
שיפוע \(8\) ו \(y\) -יירוט \((0,−6)\)
- תשובה
-
\(y=8x−6\)
שיפוע \(−1\) ו \(y\) -יירוט \((0,3)\)
שיפוע \(−1\) ו \(y\) -יירוט \((0,7)\)
- תשובה
-
\(y=−x+7\)
שיפוע \(−2\) ו \(y\) -יירוט \((0,−3)\)
שיפוע \(−3\) ו \(y\) -יירוט \((0,−1)\)
- תשובה
-
\(y=−3x−1\)
שיפוע \(\frac{3}{5}\) ו \(y\) -יירוט \((0,-1)\)
שיפוע \(\frac{1}{5}\) ו \(y\) -יירוט \((0,-5)\)
- תשובה
-
\(y=\frac{1}{5} x-5\)
שיפוע \(-\frac{3}{4}\) ו \(y\) -יירוט \((0,-2)\)
שיפוע \(-\frac{2}{3}\) ו \(y\) -יירוט \((0,-3)\)
- תשובה
-
\(y=-\frac{2}{3} x-3\)
שיפוע \(0\) ו \(y\) -יירוט \((0,-1)\)
שיפוע \(0\) ו \(y\) -יירוט \((0,2)\)
- תשובה
-
\(y=2\)
שיפוע \(-3\) ו \(y\) -יירוט \((0,0)\)
שיפוע \(-4\) ו \(y\) -יירוט \((0,0)\)
- תשובה
-
\(y=−4x\)
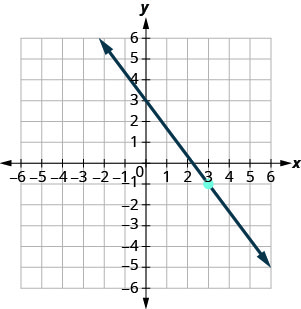
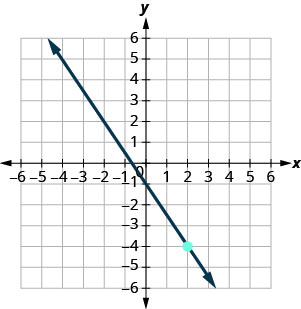
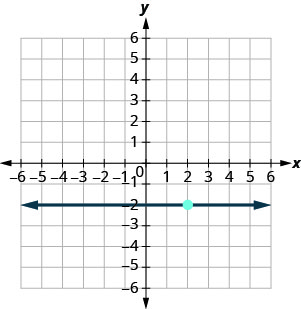
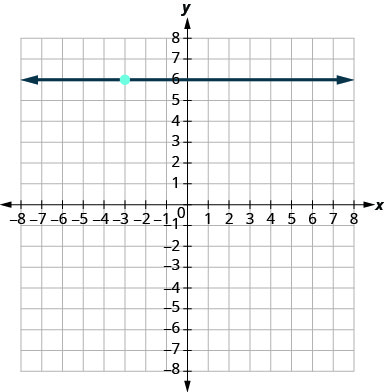
בתרגילים הבאים, מצא את משוואת הקו המוצג בכל גרף. כתוב את המשוואה בצורת שיפוע — יירוט.
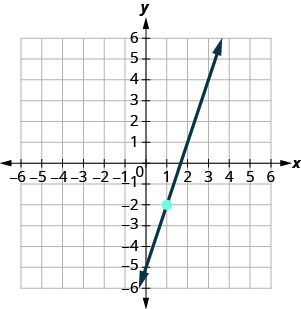
- תשובה
-
\(y=−2x+4\)
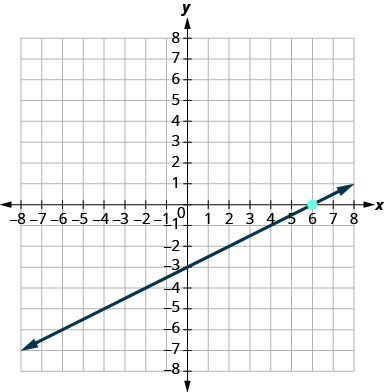
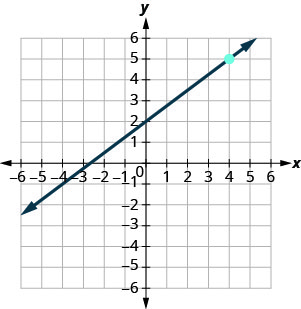
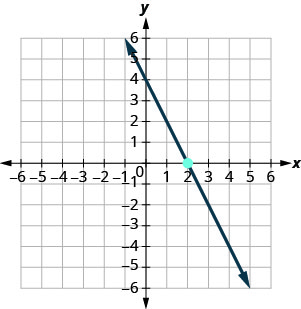
- תשובה
-
\(y=\frac{3}{4} x+2\)
- תשובה
-
\(y=-\frac{3}{2} x-1\)
- תשובה
-
\(y=6\)
מצא משוואה של הקו בהינתן המדרון ונקודה
בתרגילים הבאים, מצא את המשוואה של קו עם שיפוע נתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(m=\frac{5}{8},\)נקודה \((8,3)\)
\(m=\frac{3}{8},\)נקודה \((8,2)\)
- תשובה
-
\(y=\frac{3}{8} x-1\)
\(m=\frac{1}{6},\)נקודה \((6,1)\)
\(m=\frac{5}{6},\)נקודה \((6,7)\)
- תשובה
-
\(y=\frac{5}{6} x+2\)
\(m=-\frac{3}{4},\)נקודה \((8,-5)\)
\(m=-\frac{3}{5},\)נקודה \((10,-5)\)
- תשובה
-
\(y=-\frac{3}{5} x+1\)
\(m=-\frac{1}{4},\)נקודה \((-12,-6)\)
\(m=-\frac{1}{3},\)נקודה \((-9,-8)\)
- תשובה
-
\(y=-\frac{1}{3} x-11\)
קו אופקי המכיל \((−2,5)\)
קו אופקי המכיל \((−1,4)\)
- תשובה
-
\(y=4\)
קו אופקי המכיל \((−2,−3)\)
קו אופקי המכיל \((−1,−7)\)
- תשובה
-
\(y=−7\)
\(m=-\frac{3}{2},\)נקודה \((-4,-3)\)
\(m=-\frac{5}{2},\)נקודה \((-8,-2)\)
- תשובה
-
\(y=-\frac{5}{2} x-22\)
\(m=-7,\)נקודה \((-1,-3)\)
\(m=-4,\)נקודה \((-2,-3)\)
- תשובה
-
\(y=-4 x-11\)
קו אופקי המכיל \((2,-3)\)
קו אופקי המכיל \((4,-8)\)
- תשובה
-
\(y=−8\)
מצא משוואה של הקו בהינתן שתי נקודות
בתרגילים הבאים, מצא את המשוואה של קו המכיל את הנקודות הנתונות. כתוב את המשוואה בצורת שיפוע — יירוט.
\((2,6)\)ו \((5,3)\)
\((3,1)\)ו \((2,5)\)
- תשובה
-
\(y=−4x+13\)
\((4,3)\)ו \((8,1)\)
\((2,7)\)ו \((3,8)\)
- תשובה
-
\(y=x+5\)
\((−3,−4)\)ו \((5−2)\)
\((−5,−3)\)ו \((4,−6)\)
- תשובה
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
\((−1,3)\)ו \((−6,−7)\)
\((−2,8)\)ו \((−4,−6)\)
- תשובה
-
\(y=7x+22\)
\((6,−4)\)ו \((−2,5)\)
\((3,−2)\)ו \((−4,4)\)
- תשובה
-
\(y=-\frac{6}{7} x+\frac{4}{7}\)
\((0,4)\)ו \((2,−3)\)
\((0,−2)\)ו \((−5,−3)\)
- תשובה
-
\(y=\frac{1}{5} x-2\)
\((7,2)\)ו \((7,−2)\)
\((4,2)\)ו \((4,−3)\)
- תשובה
-
\(x=4\)
\((−7,−1)\)ו \((−7,−4)\)
\((−2,1)\)ו \((−2,−4)\)
- תשובה
-
\(x=−2\)
\((6,1)\)ו \((0,1)\)
\((6,2)\)ו \((−3,2)\)
- תשובה
-
\(y=2\)
\((3,−4)\)ו \((5,−4)\)
\((−6,−3)\)ו \((−1,−3)\)
- תשובה
-
\(y=−3\)
\((4,3)\)ו \((8,0)\)
\((0,0)\)ו \((1,4)\)
- תשובה
-
\(y=4x\)
\((−2,−3)\)ו \((−5,−6)\)
\((−3,0)\)ו \((−7,−2)\)
- תשובה
-
\(y=\frac{1}{2} x+\frac{3}{2}\)
\((8,−1)\)ו \((8,−5)\)
\((3,5)\)ו \((−7,5)\)
- תשובה
-
\(y=5\)
מצא משוואה של קו מקביל לקו נתון
בתרגילים הבאים, מצא משוואה של קו מקביל לקו הנתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(y=4 x+2,\)נקודת קו \((1,2)\)
\(y=3 x+4,\)נקודת קו \((2,5)\)
- תשובה
-
\(y=3 x-1\)
\(y=-2 x-3,\)נקודת קו \((-1,3)\)
\(y=-3x-1,\)נקודת קו \((2,-3)\)
- תשובה
-
\(y=−3x+3\)
\(3 x-y=4,\)נקודת קו \((3,1)\)
\(2 x-y=6,\)נקודת קו \((3,0)\)
- תשובה
-
\(y=2x−6\)
\(4 x+3 y=6,\)נקודת קו \((0,-3)\)
\(2x+3y=6,\)נקודת קו \((0,5)\)
- תשובה
-
\(y=-\frac{2}{3} x+5\)
\(x=-3,\)נקודת קו \((-2,-1)\)
\(x=-4,\)נקודת קו \((-3,-5)\)
- תשובה
-
\(x=−3\)
\(x-2=0,\)נקודת קו \((1,-2)\)
\(x-6=0,\)נקודת קו \((4,-3)\)
- תשובה
-
\(x=4\)
\(y=5,\)נקודת קו \((2,-2)\)
\(y=1,\)נקודת קו \((3,-4)\)
- תשובה
-
\(y=−4\)
\(y+2=0,\)נקודת קו \((3,-3)\)
\(y+7=0,\)נקודת קו \((1,-1)\)
- תשובה
-
\(y=−1\)
מצא משוואה של קו בניצב לקו נתון
בתרגילים הבאים, מצא משוואה של קו בניצב לקו הנתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(y=-2 x+3,\)נקודת קו \((2,2)\)
\(y=-x+5,\)נקודת קו \((3,3)\)
- תשובה
-
\(y=x\)
\(y=\frac{3}{4} x-2,\)נקודת קו \((-3,4)\)
\(y=\frac{2}{3} x-4,\)נקודת קו \((2,-4)\)
- תשובה
-
\(y=-\frac{3}{2} x-1\)
\(2 x-3 y=8,\)נקודת קו \((4,-1)\)
\(4 x-3 y=5,\)נקודת קו \((-3,2)\)
- תשובה
-
\(y=-\frac{3}{4} x-\frac{1}{4}\)
\(2 x+5 y=6,\)נקודת קו \((0,0)\)
\(4 x+5 y=-3,\)נקודת קו \((0,0)\)
- תשובה
-
\(y=\frac{5}{4} x\)
\(y-3=0,\)נקודת קו \((-2,-4)\)
\(y-6=0,\)נקודת קו \((-5,-3)\)
- תשובה
-
\(x=-5\)
קו \(y\) ציר, נקודה \((3,4)\)
קו \(y\) ציר, נקודה \((2,1)\)
- תשובה
-
\(y=1\)
תרגול מעורב
בתרגילים הבאים, מצא את המשוואה של כל שורה. כתוב את המשוואה בצורת שיפוע — יירוט.
מכיל את הנקודות \((4,3)\) ו \((8,1)\)
מכיל את הנקודות \((2,7)\) ו \((3,8)\)
- תשובה
-
\(y=x+5\)
\(m=\frac{1}{6},\)המכיל נקודה \((6,1)\)
\(m=\frac{5}{6},\)המכיל נקודה \((6,7)\)
- תשובה
-
\(y=\frac{5}{6} x+2\)
במקביל לקו \(4 x+3 y=6,\) המכיל נקודה \((0,-3)\)
במקביל לקו \(2 x+3 y=6,\) המכיל נקודה \((0,5)\)
- תשובה
-
\(y=-\frac{2}{3} x+5\)
\(m=-\frac{3}{4},\)המכיל נקודה \((8,-5)\)
\(m=-\frac{3}{5},\)המכיל נקודה \((10,-5)\)
- תשובה
-
\(y=-\frac{3}{5} x+1\)
בניצב \(y-1=0,\) לנקודת הקו \((-2,6)\)
בניצב לקו ציר y, נקודה \((-6,2)\)
- תשובה
-
\(y=2\)
מכיל את הנקודות \((4,3)\) ו \((8,1)\)
מכיל את הנקודות \((-2,0)\) ו \((-3,-2)\)
- תשובה
-
\(y=x+2\)
במקביל לקו \(x=-3,\) המכיל נקודה \((-2,-1)\)
במקביל לקו \(x=-4,\) המכיל נקודה \((-3,-5)\)
- תשובה
-
\(x=-3\)
מכיל את הנקודות \((-3,-4)\) ו \((2,-5)\)
מכיל את הנקודות \((-5,-3)\) ו \((4,-6)\)
- תשובה
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
בניצב לקו \(x-2 y=5,\) המכיל נקודה \((-2,2)\)
בניצב לקו \(4 x+3 y=1,\) המכיל נקודה \((0,0)\)
- תשובה
-
\(y=\frac{3}{4} x\)
מתמטיקה יומיומית
כולסטרול. הגיל, \(x,\) וכולסטרול LDL evel, \(y,\) של שני גברים ניתנים על ידי הנקודות \((18,68)\) ו \((27,122) .\) מצא משוואה לינארית המדגמת את הקשר בין גיל לרמת כולסטרול LDL.
צריכת דלק. העיר mpg,\(x\), ו-mpg הכביש המהיר, \(y,\) של שתי מכוניות ניתנות על ידי הנקודות \((29,40)\) \((19,28) .\) ומצא משוואה
ליניארית המדגמת את הקשר בין mpg עירוני לכביש המהיר mp.
- תשובה
-
\(y=1.2 x+5.2\)
תרגילי כתיבה
מדוע כל הקווים האופקיים מקבילים?
הסבירו במילים שלכם מדוע במורדות של שני קווים בניצב חייבים להיות סימנים הפוכים.
- תשובה
-
התשובות ישתנו.
בדיקה עצמית
א. לאחר השלמת התרגילים, השתמש ברשימת בדיקה זו כדי להעריך את שליטתך ביעדי סעיף זה.
ב. בסולם של 1-10, כיצד היית מדרג את השליטה שלך בסעיף זה לאור התגובות שלך ברשימת הבדיקה? איך אתה יכול לשפר את זה?


