Home
עברית
אלגברה יסודית 1e (OpenStax)
4: גרפים
4.7: גרפים של אי שוויון לינארי

4.7: גרפים של אי שוויון לינארי

Last updated
Save as PDF

Page ID: 205695

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

מטרות למידה

בסוף פרק זה, תוכל:

אמת פתרונות לאי שוויון בשני משתנים
הכירו את הקשר בין הפתרונות של אי שוויון לגרף שלו
גרף אי שוויון לינארי

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

לפתור: $4x+3>23.$
אם פספסת בעיה זו, עיין בתרגיל 2.7.22.
תרגם מאלגברה לאנגלית: $x<5.$
אם פספסת את הבעיה, סקור את תרגיל 1.3.1.
הערך $3x−2y$ מתי $x=1, \, y=−2.$
אם פספסת בעיה זו, עיין בתרגיל 1.5.28.

אמת פתרונות לאי שוויון בשני משתנים

למדנו כיצד לפתור אי שוויון במשתנה אחד. כעת, נבחן את אי השוויון בשני משתנים. לאי-שוויון בשני משתנים יש יישומים רבים. אם ניהלת עסק, למשל, היית רוצה שההכנסות שלך יהיו גדולות מהעלויות שלך - כדי שהעסק שלך ירוויח.

אי שוויון לינארי

אי שוויון לינארי הוא אי שוויון שניתן לכתוב באחת מהצורות הבאות:

\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]

איפה $A$ ולא $B$ שניהם אפס.

האם אתה זוכר שלאי שוויון עם משתנה אחד היו פתרונות רבים? הפתרון לאי-השוויון $x>3$ הוא מספר גדול יותר מ$3$. הראינו זאת בשורת המספרים על ידי הצללה בשורת המספרים מימין$3$, והצבת סוגריים פתוחים ב$3$. ראה איור$\PageIndex{1}$.

האיור מציג קו מספר המשתרע בין 5 ל -5 שלילי. סוגריים מוצגים בחיובי 3 וחץ משתרע בצורה חיובית 3 עד אינסוף חיובי. — איור $\PageIndex{1}$

באופן דומה, לאי-שוויון בשני משתנים יש פתרונות רבים. כל זוג מסודר $ (x, y)$ שהופך את אי השוויון לאמיתי כאשר אנו מחליפים בערכים הוא פיתרון של אי השוויון.

פתרון של אי שוויון ליניארי

זוג מסודר $ (x, y)$ הוא פתרון של אי שוויון ליניארי אם אי השוויון נכון כאשר אנו מחליפים את הערכים של $x$ ו$y$.

תרגיל $\PageIndex{1}$

קבע אם כל זוג מסודר הוא פיתרון לאי השוויון$y>x+4$:

$(0,0)$
$(1,6)$
$(2,6)$
$(−5,−15)$
$(−8,12)$

תשובה

$(0,0)$		$.$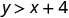
$.$		$.$
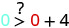
לפשט.	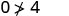	$.$ אז, $(0,0)$ הוא לא פתרון$y>x+4$.

$(1,6)$		$.$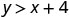
$.$		$.$
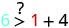
לפשט.	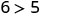	$.$ אז, $(1,6)$ הוא פתרון$y>x+4$.

$(2,6)$		$.$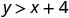
$.$		$.$
לפשט.	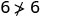	$.$ אז, $(2,6)$ הוא לא פתרון$y>x+4$.

$(−5,−15)$		$.$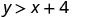
$.$		$.$
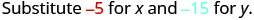
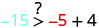
לפשט.	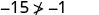	$.$ אז, $(−5,−15)$ הוא לא פתרון$y>x+4$.

(-8,12)		$.$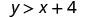
$.$		$.$
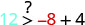
לפשט.	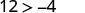	$.$ אז, $(−8,12)$ הוא פתרון$y>x+4$.

תרגיל $\PageIndex{2}$

קבע אם כל זוג מסודר הוא פיתרון לאי השוויון$y>x−3$:

$(0,0)$
$(4,9)$
$(−2,1)$
$(−5,−3)$
$(5,1)$

תשובה

כן
כן
כן
כן
לא

תרגיל $\PageIndex{3}$

קבע אם כל זוג מסודר הוא פיתרון לאי השוויון$y<x+1$:

$(0,0)$
$(8,6)$
$(−2,−1)$
$(3,4)$
$(−1,−4)$

תשובה

כן
כן
לא
לא
כן

הכירו את הקשר בין פתרונות אי השוויון לבין הגרף שלו

כעת, נבחן כיצד הפתרונות של אי שוויון קשורים לגרף שלו.

בואו נחשוב $\PageIndex{1}$ שוב על שורת המספרים באיור. הנקודה $x=3$ הפרידה את קו המספרים לשני חלקים. בצד אחד של כל $3$ המספרים פחות מ$3$. בצד השני של $3$ כל המספרים גדולים מ$3$. ראה איור$\PageIndex{2}$.

האיור מציג קו מספר המשתרע בין 5 ל -5 שלילי. סוגריים מוצגים בחיובי 3 וחץ משתרע בצורה חיובית 3 עד אינסוף חיובי. חץ מעל קו המספרים משתרע מ -3 ומצביע שמאלה. הוא מסומן "מספרים פחות מ -3." חץ מעל קו המספרים משתרע מ -3 ומצביע ימינה. הוא מסומן "מספרים גדולים מ -3." — איור $\PageIndex{2}$

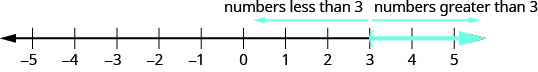
הפתרון $x>3$ הוא החלק המוצל של שורת המספרים מימין$x=3$.

באופן דומה, הקו $y=x+4$ מפריד את המטוס לשני אזורים. בצד אחד של הקו נקודות עם$y<x+4$. בצד השני של הקו הן נקודות עם$y>x+4$. אנו קוראים לקו $y=x+4$ קו גבול.

קו גבול

הקו עם המשוואה $Ax+By=C$ הוא קו הגבול המפריד בין האזור $Ax+By>C$ שממנו לאזור שבו$Ax+By<C$.

עבור אי שוויון במשתנה אחד, נקודת הקצה מוצגת עם סוגריים או סוגר, תלוי אם aa כלול בפתרון או לא:

$האיור מציג שתי שורות מספר. שורת המספרים בצד שמאל מסומנת x קטנה מ- a. שורת המספרים מציגה סוגריים ב- a וחץ המצביע שמאלה. שורת המספרים מימין מסומנת x קטנה או שווה ל- a. שורת המספרים מציגה סוגר ב- a וחץ המצביע שמאלה.$

באופן דומה, עבור אי שוויון בשני משתנים, קו הגבול מוצג עם קו מוצק או מקווקו כדי לציין אם זה הקו כלול בפתרון או לא. זה מסוכם בטבלה$\PageIndex{1}$.

טבלה $\PageIndex{1}$
$Ax+By<C$	$Ax+By\leq C$
$Ax+By>C$	$Ax+By\geq C$
קו הגבול אינו כלול בפתרון.	קו הגבול כלול בפתרון.
קו הגבול מקווקו.	קו הגבול הוא מוצק.

עכשיו, בואו נסתכל על מה שמצאנו בפעילות גופנית$\PageIndex{1}$. נתחיל בתרשים הקו$y=x+4$, ואז נתווה את חמש הנקודות שבדקנו. ראה איור$\PageIndex{3}$.

הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה ל- x פלוס 4 מתווה כחץ המשתרע משמאל למטה לכיוון הימני העליון. הנקודות הבאות מתוארות ומתויגות (שלילי 8, 12), (1, 6), (2, 6), (0, 0) ו- (שלילי 5, שלילי 15). — איור $\PageIndex{3}$

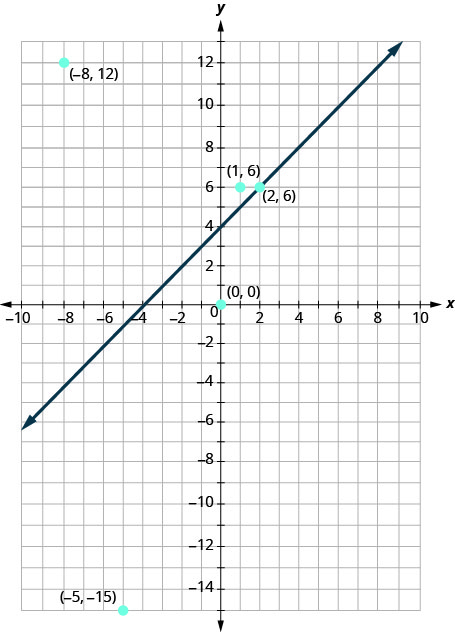
בתרגיל $\PageIndex{1}$ גילינו שחלק מהנקודות היו פתרונות לאי השוויון $y>x+4$ וחלקן לא.

אילו מהנקודות שרטטנו הן פתרונות לאי השוויון$y>x+4$? הנקודות $(1,6)$ והן $(−8,12)$ פתרונות לאי השוויון$y>x+4$. שימו לב ששניהם נמצאים באותו צד של קו הגבול$y=x+4$.

שתי הנקודות $(0,0)$ $(−5,−15)$ נמצאות בצד השני של קו הגבול$y=x+4$, והן אינן פתרונות לאי השוויון$y>x+4$. עבור שתי הנקודות האלה, $y<x+4$

מה לגבי הנקודה$(2,6)$? מכיוון $6=2+4$ שהנקודה היא פיתרון למשוואה$y=x+4$. אז הנקודה $(2,6)$ היא על קו הגבול.

בואו ניקח נקודה נוספת בצד שמאל של קו הגבול ונבדוק אם זה פיתרון לאי-השוויון או לא$y>x+4$. הנקודה נראית $(0,10)$ בבירור משמאל לקו הגבול, לא? האם זה פתרון לחוסר השוויון?

\[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]

כל נקודה שתבחר בצד שמאל של קו הגבול היא פתרון לאי השוויון$y>x+4$. כל הנקודות משמאל הן פתרונות.

באופן דומה, כל הנקודות בצד ימין של קו הגבול, הצד עם $(0,0)$ ו$(−5,−15)$, אינן פתרונות$y>x+4$. ראה איור$\PageIndex{4}$.

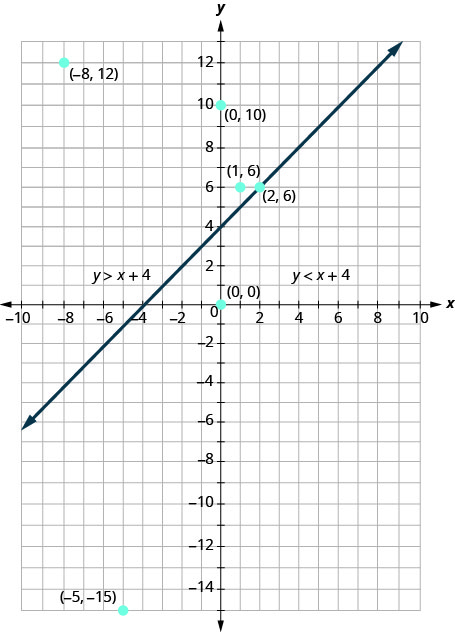
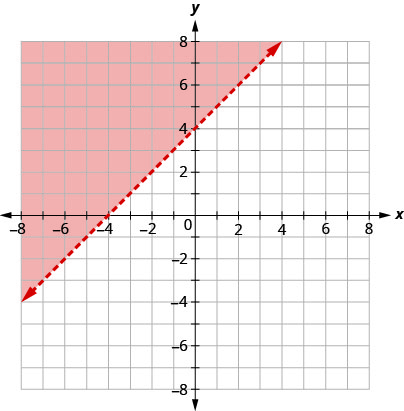
הגרף של אי השוויון $y>x+4$ מוצג ב דמות $\PageIndex{5}$ לְהַלָן. הקו $y=x+4$ מחלק את המטוס לשני אזורים. הצד המוצל מראה את הפתרונות לאי השוויון$y>x+4$.

הנקודות בקו הגבול, אלה שבהן$y=x+4$, אינן פתרונות לאי-השוויון$y>x+4$, ולכן הקו עצמו אינו חלק מהפתרון. אנו מראים כי על ידי הפיכת הקו מקווקו, לא מוצק.

הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה ל- x פלוס 4 מתווה כחץ מקווקו המשתרע משמאל למטה לכיוון הימני העליון. מישור הקואורדינטות בפינה השמאלית העליונה של הקו מוצל. — איור$\PageIndex{5}$: הגרף של אי השוויון y>x+4.

תרגיל $\PageIndex{4}$

קו הגבול המוצג הוא$y=2x−1$. כתוב את אי השוויון שמוצג על ידי הגרף.

תשובה

הקו $y=2x−1$ הוא קו הגבול. בצד אחד של הקו נמצאות הנקודות עם $y>2x−1$ ובצד השני של הקו הנקודות עם$y<2x−1$.

בואו נבדוק את הנקודה $(0,0)$ ונראה איזה אי שוויון מתאר את הצד שלה בקו הגבול.

ב$(0,0)$, איזה אי שוויון נכון:

\[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]

מכיוון $y>2x−1$ שזה נכון, הצד של הקו עם$(0,0)$, הוא הפיתרון. האזור המוצל מראה את פיתרון אי השוויון$y>2x−1$.

מכיוון שקו הגבול מתואר בקו אחיד, אי השוויון כולל את הסימן השווה.

הגרף מראה את אי השוויון$y\geq 2x−1$.

נוכל להשתמש בכל נקודה כנקודת מבחן, בתנאי שהיא לא על הקו. מדוע בחרנו$(0,0)$? כי זה הכי קל להעריך. ייתכן שתרצה לבחור נקודה בצד השני של קו הגבול ולבדוק זאת$y<2x−1$.

תרגיל $\PageIndex{5}$

כתוב את אי השוויון שמוצג על ידי הגרף עם קו הגבול$y=−2x+3$.

תשובה: $y\geq −2x+3$

תרגיל $\PageIndex{6}$

כתוב את אי השוויון שמוצג על ידי הגרף עם קו הגבול$y=\frac{1}{2}x−4$.

תשובה: $y \leq \frac{1}{2}x - 4$

תרגיל $\PageIndex{7}$

קו הגבול המוצג הוא$2x+3y=6$. כתוב את אי השוויון שמוצג על ידי הגרף.

תשובה

הקו $2x+3y=6$ הוא קו הגבול. בצד אחד של הקו נמצאות הנקודות עם $2x+3y>6$ ובצד השני של הקו הנקודות עם$2x+3y<6$.

בואו נבדוק את הנקודה $(0,0)$ ונראה איזה אי שוויון מתאר את הצד שלה בקו הגבול.

ב$(0,0)$, איזה אי שוויון נכון:

\[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]

אז הצד עם $(0,0)$ הוא הצד שבו$2x+3y<6$.

(ייתכן שתרצה לבחור נקודה בצד השני של קו הגבול ולבדוק זאת$2x+3y>6$.)

מכיוון שקו הגבול מתואר כקו מקווקו, אי השוויון אינו כולל סימן שווה.

הגרף מציג את הפיתרון לאי השוויון$2x+3y<6$.

תרגיל $\PageIndex{8}$

כתוב את אי השוויון שמוצג על ידי האזור המוצל בגרף עם קו הגבול$x−4y=8$.

תשובה: $x-4 y \leq 8$

תרגיל $\PageIndex{9}$

כתוב את אי השוויון שמוצג על ידי האזור המוצל בגרף עם קו הגבול$3x−y=6$.

תשובה: $3 x-y \leq 6$

גרף אי שוויון לינארי

כעת, אנו מוכנים לחבר את כל זה כדי לתאר את אי השוויון הליניארי.

תרגיל $\PageIndex{10}$: How to Graph Linear Inequalities

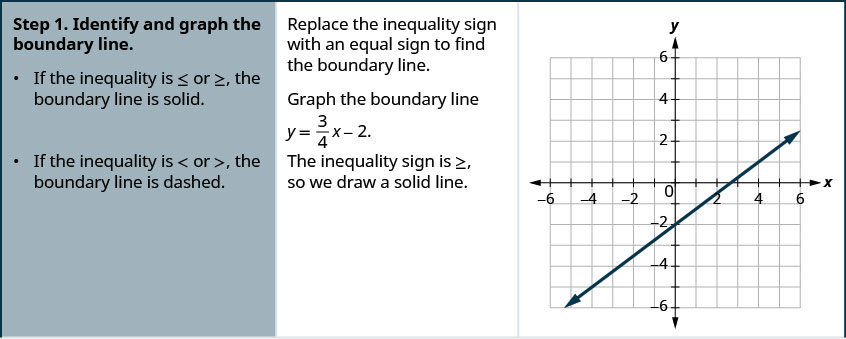
גרף את אי השוויון הליניארי$y \geq \frac{3}{4} x-2$.

תשובה: $נתון זה הוא טבלה הכוללת שלוש עמודות ושלוש שורות. העמודה הראשונה היא עמודת כותרת, והיא מכילה את השמות והמספרים של כל שלב. העמודה השנייה מכילה הוראות כתובות נוספות. העמודה השלישית מכילה מתמטיקה. בשורה העליונה של הטבלה, התא הראשון משמאל קורא: "שלב 1. זהה וגרף את קו הגבול. אם אי השוויון קטן או שווה או גדול או שווה לו, קו הגבול מוצק. אם אי השוויון קטן או גדול מ-, קו הגבול מקווקו. הטקסט בתא השני כתוב: "החלף את סימן האי-שוויון בסימן שווה כדי למצוא את קו הגבול. גרף קו הגבול y שווה לשלושה רבעים x מינוס 2. סימן האי-שוויון גדול או שווה ל, ולכן אנו מציירים קו מוצק. התא השלישי מכיל את הגרף של הקו שלושה רבעים x מינוס 2 במישור קואורדינטות.$ $בשורה השנייה של הטבלה, התא הראשון אומר: "שלב 2. בדוק נקודה שאינה על קו הגבול. האם זה פתרון של אי השוויון? בתא השני, ההוראות אומרות: "נבדוק (0, 0). האם זה פתרון של אי השוויון?" התא השלישי שואל: ב (0, 0), האם y גדול או שווה לשלושה רבעים x מינוס 2? מתחת לזה אי השוויון 0 גדול או שווה לשלושה רבעים 0 מינוס 2, עם סימן שאלה מעל סמל אי השוויון. מתחת לזה אי השוויון 0 גדול או שווה לשלילי 2. 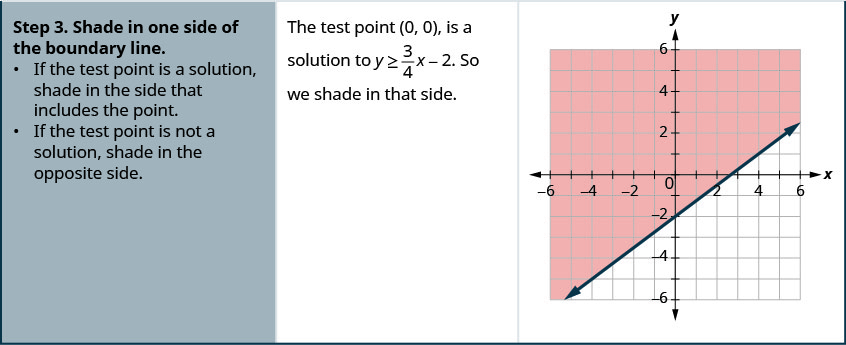להלן: "אז (0, 0) הוא פיתרון.$ $בשורה השלישית של הטבלה, התא הראשון אומר: "שלב 3. צל בצד אחד של קו הגבול. אם נקודת הבדיקה היא פתרון, צל בצד הכולל את הנקודה. אם נקודת הבדיקה אינה פתרון, צל בצד הנגדי. בתא השני ההוראות אומרות: נקודת הבדיקה (0, 0) היא פיתרון ל- y גדול או שווה לשלושה רבעים x מינוס 2. אז אנחנו מצללים בצד הזה." בתא השלישי נמצא הגרף של הקו שלושה רבעים x מינוס 2 במישור קואורדינטות כשהאזור מעל הקו מוצל.$

תרגיל $\PageIndex{11}$

גרף את אי השוויון הליניארי$y \geq \frac{5}{2} x-4$.

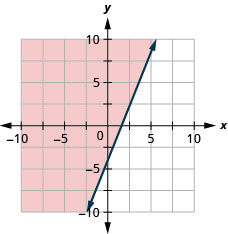
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה לחמישה חצאים x מינוס 4 מתווה כחץ מוצק המשתרע משמאל למטה לכיוון ימין למעלה. האזור שמעל לקו מוצל.$

תרגיל $\PageIndex{12}$

גרף את אי השוויון הליניארי$y<\frac{2}{3} x-5$.

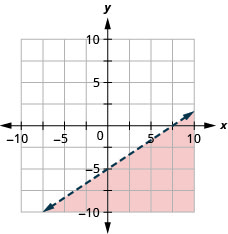
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה לשני שלישים x מינוס 5 מתווה כחץ מקווקו המשתרע משמאל למטה לכיוון ימין למעלה. האזור שמתחת לקו מוצל.$

הצעדים שאנו נוקטים כדי לתאר אי שוויון ליניארי מסוכמים כאן.

גרף אי שוויון ליניארי.

זהה וגרף את קו הגבול.
- אם אי השוויון הוא $≤$ או$≥$, קו הגבול מוצק.
- אם אי השוויון הוא $<$ או$>$, קו הגבול מקווקו.
בדוק נקודה שאינה על קו הגבול. האם זה פתרון של אי השוויון?
צל בצד אחד של קו הגבול.
- אם נקודת הבדיקה היא פתרון, צל בצד הכולל את הנקודה.
- אם נקודת הבדיקה אינה פתרון, צל בצד הנגדי.

תרגיל $\PageIndex{13}$

גרף את אי השוויון הליניארי$x−2y<5$.

תשובה

ראשית אנו משרטטים את קו הגבול$x−2y=5$. אי השוויון הוא $<$ כך שאנו מציירים קו מקווקו.

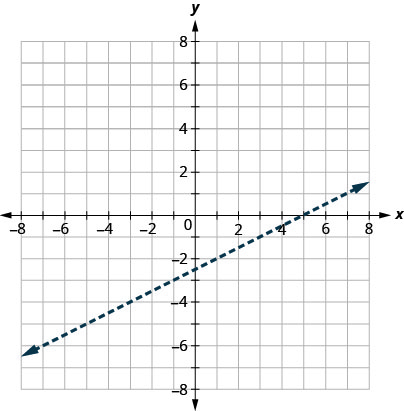
$הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו x מינוס 2 y שווה ל -5 מתווה כחץ מקווקו המשתרע משמאל למטה לכיוון ימין למעלה.$

ואז אנו בודקים נקודה. נשתמש $(0,0)$ שוב כי זה קל להעריך וזה לא על קו הגבול.

האם $(0,0)$ פתרון של$x−2y<5$?

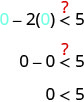
$האיור מראה את אי השוויון 0 מינוס 2 פעמים 0 בסוגריים הוא פחות מ -5, עם סימן שאלה מעל סמל אי השוויון. השורה הבאה מציגה 0 מינוס 0 הוא פחות מ -5, עם סימן שאלה מעל סמל אי השוויון. השורה השלישית מראה 0 הוא פחות מ 5.$

הנקודה $(0,0)$ היא פתרון של$x−2y<5$, אז אנחנו צל בצד הזה של קו הגבול.

תרגיל $\PageIndex{14}$

גרף את אי השוויון הליניארי$2x−3y\leq 6$.

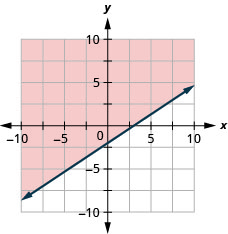
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו 2 x מינוס 3 y שווה ל 6 מתווה כחץ מוצק המשתרע משמאל למטה לכיוון ימין למעלה. האזור שמעל לקו מוצל.$

תרגיל $\PageIndex{15}$

גרף את אי השוויון הליניארי$2x−y>3$.

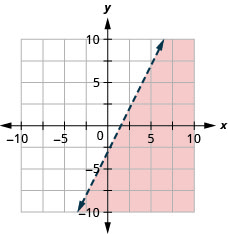
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו 2 x מינוס y שווה ל -3 מתווה כחץ מקווקו המשתרע משמאל למטה לכיוון ימין למעלה. האזור שמתחת לקו מוצל.$

מה אם קו הגבול עובר דרך המקור? אז לא נוכל להשתמש $(0,0)$ כנקודת מבחן. אין בעיה - פשוט נבחר נקודה אחרת שאינה על קו הגבול.

תרגיל $\PageIndex{16}$

גרף את אי השוויון הליניארי$y\leq −4x$.

תשובה

ראשית אנו משרטטים את קו הגבול$y=−4x$. זה בצורת שיפוע - יירוט, עם ו. $m=−4$ $b=0$ אי השוויון הוא $≤$ כך שאנו מציירים קו מוצק.

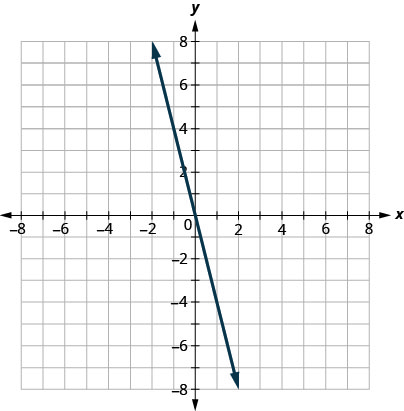
$הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו s y שווה לשלילי 4 x משורטט כחץ מוצק המשתרע משמאל למעלה לכיוון ימין למטה.$

עכשיו, אנחנו צריכים נקודת מבחן. אנו יכולים לראות שהנקודה $(1,0)$ אינה על קו הגבול.

האם $(1,0)$ פתרון של$y≤−4x$?

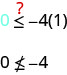
$האיור מראה ש- 0 פחות או שווה לשלילי 4 פעמים 1 בסוגריים, עם סימן שאלה מעל סמל אי השוויון. השורה הבאה מראה 0 הוא לא פחות או שווה לשלילי 4.$

הנקודה $(1,0)$ היא לא פתרון$y≤−4x$, אז אנחנו צל בצד הנגדי של קו הגבול. ראה איור$\PageIndex{6}$.

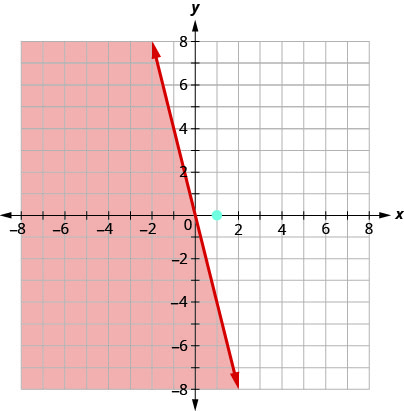
הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה לשלילי 4 x משורטט כחץ מוצק המשתרע משמאל למעלה לכיוון ימין למטה. הנקודה (1, 0) משורטטת, אך אינה מסומנת. האזור משמאל לקו מוצל. — איור $\PageIndex{6}$

תרגיל $\PageIndex{17}$

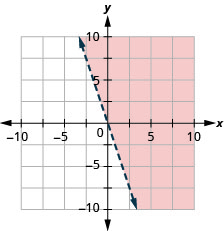
גרף את אי השוויון הליניארי$y>−3x$.

תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה ל -3 x שלילי משורטט כחץ מקווקו המשתרע משמאל למעלה לכיוון ימין למטה. האזור מימין לקו מוצל.$

תרגיל $\PageIndex{18}$

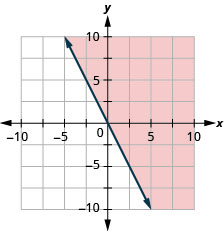
גרף את אי השוויון הליניארי$y\geq −2x$.

תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה לשלילי 2 x משורטט כחץ מוצק המשתרע משמאל למעלה לכיוון ימין למטה. האזור מימין לקו מוצל.$

לחלק מהאי-שוויון הליניארי יש רק משתנה אחד. אולי יש להם $x$ אבל לא$y$, או $y$ אבל לא$x$. במקרים אלה, קו הגבול יהיה קו אנכי או אופקי. האם אתה זוכר?

$\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}$

תרגיל $\PageIndex{19}$

גרף את אי השוויון הליניארי$y>3$.

תשובה

ראשית אנו משרטטים את קו הגבול$y=3$. זהו קו אופקי. אי השוויון הוא $>$ כך שאנו מציירים קו מקווקו.

אנחנו בודקים את הנקודה$(0,0)$.

\[y>3 \\ 0\not>3\]

$(0,0)$זה לא פתרון ל$y>3$.

אז אנחנו מצללים את הצד שאינו כולל$(0,0)$.

תרגיל $\PageIndex{20}$

גרף את אי השוויון הליניארי$y<5$.

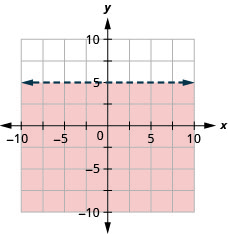
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה ל -5 מתווה כחץ מקווקו אופקית על פני המישור. האזור שמעל לקו מוצל.$

תרגיל $\PageIndex{21}$

גרף את אי השוויון הליניארי$y \leq-1$.

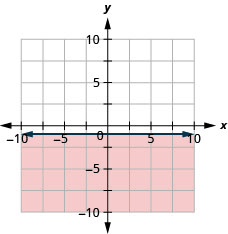
תשובה: $הגרף מציג את מישור הקואורדינטות x y. צירי ה- x ו- y עוברים כל אחד מ -10 ל -10 שלילי. הקו y שווה לשלילי 1 משורטט כחץ מקווקו אופקית על פני המישור. האזור שמתחת לקו מוצל.$

מושגי מפתח

לתרשים אי שוויון לינארי
1. זהה וגרף את קו הגבול.
  אם אי השוויון הוא $≤$ או$≥$, קו הגבול מוצק.
  אם אי השוויון הוא $<$ או$>$, קו הגבול מקווקו.
2. בדוק נקודה שאינה על קו הגבול. האם זה פתרון של אי השוויון?
3. צל בצד אחד של קו הגבול.
  אם נקודת הבדיקה היא פתרון, צל בצד הכולל את הנקודה.
  אם נקודת הבדיקה אינה פתרון, צל בצד הנגדי.

רשימת מילים

קו גבול: הקו עם משוואה $A x+B y=C$ המפריד בין האזור $A x+B y>C$ שממנו לאזור שבו$A x+B y<C$.

אי שוויון לינארי: אי שוויון שניתן לכתוב באחת מהצורות הבאות:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]
איפה $A$ ולא $B$ שניהם אפס.

פתרון של אי שוויון ליניארי: זוג מסודר $(x,\,y)$ הוא פתרון לאי שוויון ליניארי אי השוויון נכון כאשר אנו מחליפים את הערכים של $x$ ו$y$.

אי שוויון לינארי

פתרון של אי שוויון ליניארי

תרגיל \(\PageIndex{1}\)

תרגיל \(\PageIndex{2}\)

תרגיל \(\PageIndex{3}\)

קו גבול

תרגיל \(\PageIndex{4}\)

תרגיל \(\PageIndex{5}\)

תרגיל \(\PageIndex{6}\)

תרגיל \(\PageIndex{7}\)

תרגיל \(\PageIndex{8}\)

תרגיל \(\PageIndex{9}\)

תרגיל \(\PageIndex{10}\): How to Graph Linear Inequalities

תרגיל \(\PageIndex{11}\)

תרגיל \(\PageIndex{12}\)

גרף אי שוויון ליניארי.

תרגיל \(\PageIndex{13}\)

תרגיל \(\PageIndex{14}\)

תרגיל \(\PageIndex{15}\)

תרגיל \(\PageIndex{16}\)

תרגיל \(\PageIndex{17}\)

תרגיל \(\PageIndex{18}\)

תרגיל \(\PageIndex{19}\)

תרגיל \(\PageIndex{20}\)

תרגיל \(\PageIndex{21}\)

\((0,0)\)		$.$
$.$		$.$
לפשט.		$.$ אז, \((0,0)\) הוא לא פתרון\(y>x+4\).

\((1,6)\)		$.$
$.$		$.$
לפשט.		$.$ אז, \((1,6)\) הוא פתרון\(y>x+4\).

\((2,6)\)		$.$
$.$		$.$
לפשט.		$.$ אז, \((2,6)\) הוא לא פתרון\(y>x+4\).

\((−5,−15)\)		$.$
$.$		$.$
לפשט.		$.$ אז, \((−5,−15)\) הוא לא פתרון\(y>x+4\).

(-8,12)		$.$
$.$		$.$
לפשט.		$.$ אז, \((−8,12)\) הוא פתרון\(y>x+4\).

\(Ax+By<C\)	\(Ax+By\leq C\)
\(Ax+By>C\)	\(Ax+By\geq C\)
קו הגבול אינו כלול בפתרון.	קו הגבול כלול בפתרון.
קו הגבול מקווקו.	קו הגבול הוא מוצק.