4.6: מצא את משוואת הקו
- Page ID
- 205762
בסוף פרק זה, תוכל:
- מצא משוואה של הקו בהינתן השיפוע והיירוט y
- מצא משוואה של הקו בהינתן המדרון ונקודה
- מצא משוואה של הקו בהינתן שתי נקודות
- מצא משוואה של קו מקביל לקו נתון
- מצא משוואה של קו בניצב לקו נתון
לפני שתתחיל, קח את חידון המוכנות הזה.
- לפתור:\(\frac{2}{3} = \frac{x}{5}\).
אם פספסת בעיה זו, עיין בתרגיל 2.2.4. - פשט:\(−\frac{2}{5}(x−15)\).
אם פספסת בעיה זו, עיין בתרגיל 1.10.34.
איך קמעונאים מקוונים יודעים ש'אולי גם תאהב' פריט מסוים המבוסס על משהו שהזמנת זה עתה? כיצד יכולים כלכלנים לדעת כיצד עליית שכר המינימום תשפיע על שיעור האבטלה? כיצד חוקרים רפואיים יוצרים תרופות למיקוד תאים סרטניים? כיצד יכולים מהנדסי תנועה לחזות את ההשפעה על זמן הנסיעה שלך לעלייה או ירידה במחירי הדלק? זה הכל מתמטיקה.
אתה נמצא בנקודה מרגשת במסע המתמטי שלך מכיוון שלמתמטיקה שאתה לומד יש יישומים מעניינים בעולם האמיתי.
מדעי הפיזיקה, מדעי החברה ועולם העסקים מלאים במצבים שניתן לדגמן באמצעות משוואות לינאריות המתייחסות לשני משתנים. הנתונים נאספים ומוצגים בתרשים. אם נראה שנקודות הנתונים יוצרות קו ישר, ניתן להשתמש במשוואה של קו זה כדי לחזות את הערך של משתנה אחד על סמך הערך של המשתנה השני.
כדי ליצור מודל מתמטי של קשר לינארי בין שני משתנים, עלינו להיות מסוגלים למצוא את משוואת הקו. בחלק זה נבחן מספר דרכים לכתוב את המשוואה של שורה. השיטה הספציפית בה אנו משתמשים תיקבע על פי המידע שניתן לנו.
מצא משוואה של הקו בהתחשב בשיפוע ו- y -יירוט
אנו יכולים לקבוע בקלות את השיפוע והיירוט של קו אם המשוואה נכתבה בצורת שיפוע - יירוט, y = mx+b כעת, נעשה את ההיפוך - נתחיל בשיפוע ו- y -יירוט ונשתמש בהם כדי למצוא את משוואת הקו.
מצא משוואה של קו עם שיפוע −7 ו- y -יירוט (0, −1).
- תשובה
-
מכיוון שאנו מקבלים את השיפוע ו- y -יירוט של הקו, אנו יכולים להחליף את הערכים הדרושים לצורת השיפוע — יירוט, y = mx+b.
תן שם למדרון. 
תן שם ליירוט y. 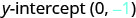
החלף את הערכים ל- y = mx+b. 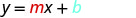
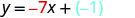
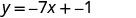
מצא משוואה של קו עם שיפוע \(\frac{2}{5}\) ו- y -יירוט (0,4).
- תשובה
-
\(y = \frac{2}{5}x + 4\)
מצא משוואה של קו עם שיפוע -1 ו- y -יירוט (0, -3).
- תשובה
-
\(y=−x−3\)
לפעמים, השיפוע והיירוט צריכים להיקבע מהגרף.
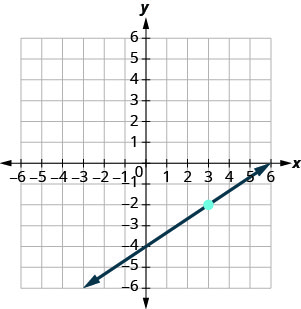
מצא את המשוואה של הקו המוצג.
- תשובה
-
עלינו למצוא את השיפוע ואת יירוט ה- y של הקו מהגרף כדי שנוכל להחליף את הערכים הדרושים לצורת השיפוע — יירוט, y=mx+by=mx+b.
כדי למצוא את המדרון, אנו בוחרים שתי נקודות בגרף.
יירוט y הוא (0, -4) והגרף עובר דרכו (3, -2).
מצא את המדרון על ידי ספירת העלייה והריצה. 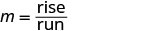

מצא את יירוט y. 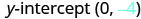
החלף את הערכים ל- y = mx+b. 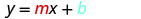
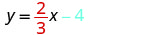
מצא את משוואת הקו המוצג בתרשים.
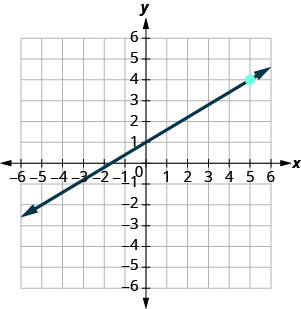
- תשובה
-
\(y=\frac{3}{5}x+1\)
מצא את משוואת הקו המוצג בתרשים.
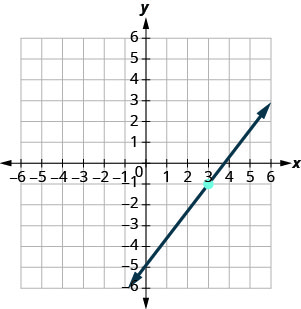
- תשובה
-
\(y=\frac{4}{3}x−5\)
מצא משוואה של הקו בהינתן המדרון ונקודה
מציאת משוואה של קו באמצעות צורת השיפוע -יירוט של המשוואה עובדת היטב כאשר מקבלים את השיפוע ו- y -יירוט או כשאתה קורא אותם מגרף. אבל מה קורה כשיש לך נקודה נוספת במקום יירוט y?
אנו הולכים להשתמש בנוסחת השיפוע כדי להפיק צורה אחרת של משוואה של הקו. נניח שיש לנו קו שיש לו שיפוע מ"מ ומכיל נקודה ספציפית כלשהי \((x_{1}, y_{1})\) ונקודה אחרת, שפשוט נקרא לה (x, y). אנו יכולים לכתוב את שיפוע השורה הזו ואז לשנות אותה לצורה אחרת.
\(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)
תבנית זו נקראת צורת נקודה-שיפוע של משוואת קו.
צורת הנקודה-שיפוע של משוואה של קו עם שיפוע מ"מ ומכילה את הנקודה היא \((x_{1}, y_{1})\)
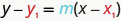
אנו יכולים להשתמש בצורת נקודה-שיפוע של משוואה כדי למצוא משוואה של קו כאשר נותנים לנו את השיפוע ונקודה אחת. לאחר מכן נכתוב מחדש את המשוואה בצורת שיפוע — יירוט. רוב היישומים של משוואות לינאריות משתמשים בצורת השיפוע -יירוט.
מצא משוואה של קו עם שיפוע \(m=\frac{2}{5}\) המכיל את הנקודה (10,3). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-




מצא משוואה של קו עם שיפוע \(m=\frac{5}{6}\) ומכיל את הנקודה (6,3).
- תשובה
-
\(y=\frac{5}{6}x−2\)
מצא משוואה של קו עם שיפוע \(m=\frac{2}{3}\) ומכיל את הנקודה (9,2).
- תשובה
-
\(y=\frac{2}{3}x−4\)
- זהה את המדרון.
- זהה את הנקודה.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת שיפוע — יירוט.
מצא משוואה של קו עם שיפוע \(m=−\frac{1}{3}\) המכיל את הנקודה (6, -4). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
מכיוון שאנו מקבלים נקודה ושיפוע הקו, אנו יכולים להחליף את הערכים הדרושים לנקודה - צורת שיפוע,. \(y−y_{1}=m(x−x_{1})\)
זהה את המדרון. 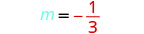
זהה את הנקודה. 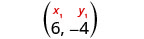
החלף את הערכים לתוך\(y−y_{1}=m(x−x_{1})\). 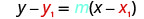
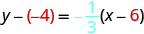
לפשט. 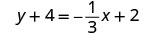
כתוב בצורה מדרון — יירוט. 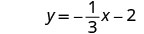
מצא משוואה של קו עם שיפוע \(m=−\frac{2}{5}\) ומכיל את הנקודה (10, -5).
- תשובה
-
\(y=−\frac{2}{5}x−1\)
מצא משוואה של קו עם שיפוע\(m=−\frac{3}{4}\), ומכיל את הנקודה (4, −7).
- תשובה
-
\(y=−\frac{3}{4}x−4\)
מצא משוואה של קו אופקי המכיל את הנקודה (-1,2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
לכל קו אופקי יש שיפוע 0. אנחנו יכולים להחליף את השיפוע ואת הנקודות לתוך הנקודה - צורת שיפוע,. \(y−y_{1}=m(x−x_{1})\)
האם בסופו של דבר קיבלנו צורה של קו אופקי, y=a?זהה את המדרון. 
זהה את הנקודה. 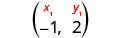
החלף את הערכים לתוך\(y−y_{1}=m(x−x_{1})\). 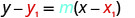
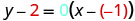
לפשט. 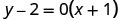
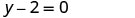
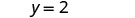
כתוב בצורה מדרון — יירוט. זה בצורת y, אבל יכול להיות כתוב y = 0x+2.
מצא משוואה של קו אופקי המכיל את הנקודה (-3,8).
- תשובה
-
y = 8
מצא משוואה של קו אופקי המכיל את הנקודה (-1,4).
- תשובה
-
y = 4
מצא משוואה של הקו בהינתן שתי נקודות
כאשר נאספים נתונים מהעולם האמיתי, ניתן ליצור מודל ליניארי משתי נקודות נתונים. בדוגמה הבאה נראה כיצד למצוא משוואה של קו כאשר ניתנות שתי נקודות בלבד.
יש לנו עד כה שתי אפשרויות למציאת משוואה של קו: שיפוע - יירוט או נקודה - שיפוע. מכיוון שנדע שתי נקודות, יהיה הגיוני יותר להשתמש בצורת הנקודה-שיפוע.
אבל אז אנחנו צריכים את המדרון. האם נוכל למצוא את המדרון עם שתי נקודות בלבד? כן. ואז, ברגע שיש לנו את המדרון, נוכל להשתמש בו ובאחת מהנקודות הנתונות כדי למצוא את המשוואה.
מצא משוואה של קו המכיל את הנקודות (5,4) ו- (3,6). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-




השתמש בנקודה (3,6) וראה שאתה מקבל את אותה משוואה.
מצא משוואה של קו המכיל את הנקודות (3,1) ו- (5,6).
- תשובה
-
\(y=\frac{5}{2}x−\frac{13}{2}\)
מצא משוואה של קו המכיל את הנקודות (1,4) ו- (6,2).
- תשובה
-
\(y=−\frac{2}{5}x+\frac{22}{5}\)
- מצא את המדרון באמצעות הנקודות הנתונות.
- בחר נקודה אחת.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת שיפוע — יירוט.
מצא משוואה של קו המכיל את הנקודות (-3, -1) ו- (2, -2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
מכיוון שיש לנו שתי נקודות, נמצא משוואה של הקו באמצעות צורת הנקודה-שיפוע. הצעד הראשון יהיה למצוא את המדרון.
מצא את שיפוע הקו דרך (-3, -1) ו- (2, -2). 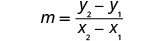
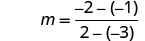
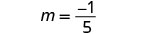
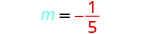
בחר אחת מהנקודה. 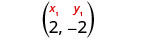
החלף את הערכים לתוך\(y−y_{1}=m(x−x_{1})\). 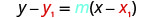
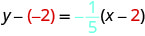
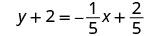
כתוב בצורה מדרון — יירוט. 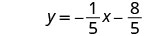
מצא משוואה של קו המכיל את הנקודות (-2, -4) ו- (1, -3).
- תשובה
-
\(y=\frac{1}{3}x−\frac{10}{3}\)
מצא משוואה של קו המכיל את הנקודות (-4, -3) ו- (1, -5).
- תשובה
-
\(y=−\frac{2}{5}x−\frac{23}{5}\)
מצא משוואה של קו המכיל את הנקודות (-2,4) ו- (-2, -3). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
שוב, הצעד הראשון יהיה למצוא את המדרון.
\(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)
זה אומר לנו שזה קו אנכי. לשתי הנקודות שלנו יש קואורדינטת x של -2. אז משוואת הקו שלנו היא איקס=−2. מכיוון שאין yy, איננו יכולים לכתוב אותו בצורה של שיפוע - יירוט.
ייתכן שתרצה לשרטט גרף באמצעות שתי הנקודות הנתונות. האם הגרף מסכים עם המסקנה שלנו שמדובר בקו אנכי?
מצא משוואה של קו המכיל את הנקודות (5,1) ו- (5, -4).
- תשובה
-
איקס = 5
מצא משוואה של קו המכיל את הנקודות (-4,4) ו- (-4,3).
- תשובה
-
איקס=−4
ראינו שאנחנו יכולים להשתמש בצורת השיפוע - יירוט או בצורת השיפוע של נקודה כדי למצוא משוואה של קו. איזו צורה אנו משתמשים תהיה תלויה במידע שניתן לנו. זה מסוכם בטבלה\(\PageIndex{1}\).
| כדי לכתוב משוואה של שורה | ||
| אם ניתן: | שימוש: | טופס: |
| שיפוע ו- y -יירוט | מדרון — יירוט | y = mx+ב |
| שיפוע ונקודה | נקודה — שיפוע | \(y−y_{1}=m(x−x_{1})\) |
| שתי נקודות | נקודה — שיפוע | \(y−y_{1}=m(x−x_{1})\) |
מצא משוואה של קו מקביל לקו נתון
נניח שאנחנו צריכים למצוא משוואה של קו שעובר דרך נקודה מסוימת והוא מקביל לקו נתון. אנו יכולים להשתמש בעובדה שלקווים מקבילים יש שיפוע זהה. אז תהיה לנו נקודה והמדרון - בדיוק מה שאנחנו צריכים כדי להשתמש במשוואת השיפוע של הנקודה.
ראשית בואו נסתכל על זה בצורה גרפית.
הגרף מציג את הגרף של y = 2x−3. אנו רוצים לשרטט קו מקביל לקו זה ועובר בנקודה (-2,1).
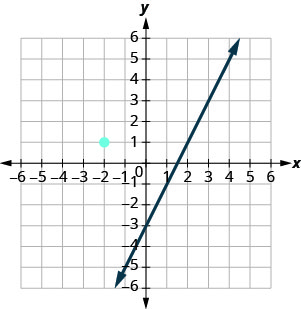
אנו יודעים שלקווים מקבילים יש שיפוע זהה. אז לקו השני יהיה שיפוע זהה לזה של y = 2x−3. המדרון הזה הוא\(m_{\|} = 2\). נשתמש בסימון \(m_{\|}\) כדי לייצג את שיפוע הקו המקביל לקו עם שיפוע m (שימו לב שהתת-המשנה נראה כמו שני קווים מקבילים.)
הקו השני יעבור דרך (-2,1) ויש לו m = 2. כדי לתאר את הקו, אנו מתחילים ב- (-2,1) וסופרים את העלייה והריצה. עם m = 2 (או\(m=\frac{2}{1}\)), אנו סופרים את העלייה 2 ואת הריצה 1. אנו מותחים את הקו.
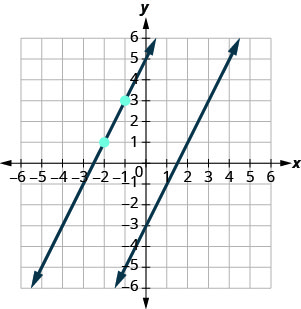
האם הקווים נראים מקבילים? האם הקו השני עובר דרך (-2,1)?
עכשיו, בואו נראה איך לעשות את זה באופן אלגברי.
אנו יכולים להשתמש בצורת השיפוע - יירוט או בצורת שיפוע הנקודה כדי למצוא משוואה של קו. כאן אנו יודעים נקודה אחת ויכולים למצוא את המדרון. אז נשתמש בצורת הנקודה-שיפוע.
מצא משוואה של קו מקביל ל y = 2x−3 המכיל את הנקודה (-2,1). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-




האם המשוואה הזו הגיונית? מהו יירוט ה- y של הקו? מהו המדרון?
מצא משוואה של קו מקביל לקו y = 3x+1 המכיל את הנקודה (4,2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
y=3איקס−10
מצא משוואה של קו מקביל לקו \(y=\frac{1}{2}x−3\) המכיל את הנקודה (6,4).
- תשובה
-
\(y=\frac{1}{2}x+1\)
- מצא את השיפוע של הקו הנתון.
- מצא את שיפוע הקו המקביל.
- זהה את הנקודה.
- החלף את הערכים לצורת הנקודה-שיפוע,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת שיפוע — יירוט.
מצא משוואה של קו בניצב לקו נתון
עכשיו, בואו ניקח בחשבון קווים בניצב. נניח שאנחנו צריכים למצוא קו עובר דרך נקודה מסוימת אשר ניצב לקו נתון. אנו יכולים להשתמש בעובדה שלקווים בניצב יש שיפועים שהם הדדיות שליליות. נשתמש שוב במשוואת נקודה-שיפוע, כמו שעשינו בקווים מקבילים.
הגרף מציג את הגרף של y = 2x−3. כעת, אנו רוצים לשרטט קו בניצב לקו זה ועובר דרכו (-2,1).

אנו יודעים שלקווים בניצב יש שיפועים שהם הדדיות שליליות. נשתמש בסימון \(m_{\perp}\) כדי לייצג את שיפוע הקו הניצב לקו עם שיפוע m (שימו לב שהתת-המשנה \(_{\perp}\) נראה כמו הזוויות הנכונות שנעשו על ידי שני קווים בניצב.)
\[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]
כעת אנו יודעים שהקו הניצב יעבור דרכו (-2,1) עם. \(m_{\perp}=−\frac{1}{2}\)
כדי לתאר את הקו, נתחיל ב- (-2,1) ונספור את העלייה -1 ואת הריצה 2. ואז אנו מציירים את הקו.
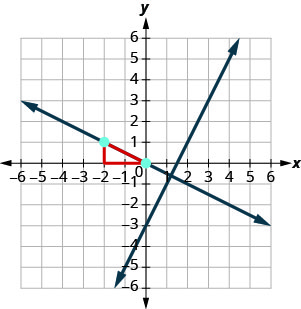
האם הקווים נראים בניצב? האם הקו השני עובר דרך (-2,1)?
עכשיו, בואו נראה איך לעשות את זה באופן אלגברי. אנו יכולים להשתמש בצורת השיפוע - יירוט או בצורת שיפוע הנקודה כדי למצוא משוואה של קו. בדוגמה זו אנו מכירים נקודה אחת, ויכולים למצוא את השיפוע, ולכן נשתמש בצורת הנקודה-שיפוע.
מצא משוואה של קו בניצב ל- y = 2x−3 המכיל את הנקודה (-2,1). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-





מצא משוואה של קו בניצב לקו y = 3x+1 המכיל את הנקודה (4,2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
\(y=−\frac{1}{3}x+\frac{10}{3}\)
מצא משוואה של קו בניצב לקו \(y=\frac{1}{2}x−3\) המכיל את הנקודה (6,4).
- תשובה
-
y = −2איקס+16
- מצא את השיפוע של הקו הנתון.
- מצא את שיפוע הקו הניצב.
- זהה את הנקודה.
- החלף את הערכים לצורת הנקודה-שיפוע,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת שיפוע — יירוט.
מצא משוואה של קו בניצב ל איקס=5 המכיל את הנקודה (3, −2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
שוב, מכיוון שאנו מכירים נקודה אחת, אפשרות הנקודה-שיפוע נראית מבטיחה יותר מאופציית היירוט של המדרון. אנו זקוקים למדרון כדי להשתמש בטופס זה, ואנו יודעים שהקו החדש יהיה בניצב ל- x = 5. קו זה הוא אנכי, כך הניצב שלו יהיה אופקי. זה אומר לנו את\(m_{\perp}=0\).
\(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)
שרטט את הגרף של שתי השורות. האם הם נראים בניצב?
מצא משוואה של קו הניצב לקו איקס=4 המכיל את הנקודה (4, −5). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
y=−5
מצא משוואה של קו הניצב לקו איקס=2 המכיל את הנקודה (2, −1). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
y=−1
בתרגיל \(\PageIndex{31}\) השתמשנו בצורת הנקודה-שיפוע כדי למצוא את המשוואה. יכולנו להסתכל על זה בצורה אחרת.
אנו רוצים למצוא קו הניצב ל איקס=5 המכיל את הנקודה (3, −2). הגרף מראה לנו את הקו איקס=5 ואת הנקודה (3, −2).
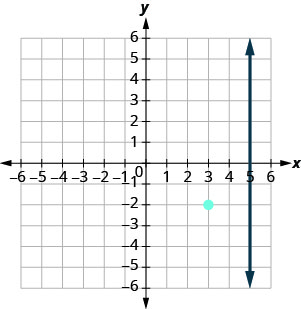
אנו יודעים שכל קו בניצב לקו אנכי הוא אופקי, ולכן נשרטט את הקו האופקי דרך (3, -2).
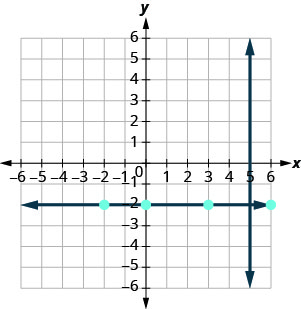
האם הקווים נראים בניצב?
אם נסתכל על כמה נקודות בקו האופקי הזה, נבחין שלכולן יש y -קואורדינטות של -2. אז, משוואת הקו הניצב לקו האנכי איקס=5 היא y = −2.
מצא משוואה של קו הניצב ל- y = −4 המכיל את הנקודה (-4,2). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
הקו y = −4 הוא קו אופקי. כל קו הניצב אליו חייב להיות אנכי, בצורה איקס=א מכיוון שהקו הניצב הוא אנכי ועובר דרכו (-4,2), לכל נקודה עליו יש קואורדינטה x של -4. המשוואה של הקו הניצב היא איקס=−4. אולי תרצה לשרטט את השורות. האם הם נראים בניצב?
מצא משוואה של קו הניצב לקו y = 1 המכיל את הנקודה (-5,1). כתוב את המשוואה בצורת שיפוע — יירוט.
- תשובה
-
איקס=−5
מצא משוואה של קו הניצב לקו y = −5 המכיל את הנקודה (-4, -5).
- תשובה
-
איקס=−4
גש למשאב מקוון זה לקבלת הדרכה ותרגול נוספים עם מציאת המשוואה של קו.
מושגי מפתח
- למצוא משוואה של קו בהינתן השיפוע ונקודה
- זהה את המדרון.
- זהה את הנקודה.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת יירוט שיפוע.
- למצוא משוואה של קו בהינתן שתי נקודות
- מצא את המדרון באמצעות הנקודות הנתונות.
- בחר נקודה אחת.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת יירוט שיפוע.
- לכתוב ומשוואת שורה
- אם ניתן שיפוע ו \(y\) -יירוט, השתמש בצורת שיפוע -יירוט. \(y=mx+b\)
- אם ניתן שיפוע ונקודה, השתמש בצורת נקודה-שיפוע. \(y−y_{1}=m(x−x_{1})\)
- אם ניתנות שתי נקודות, השתמש בצורת נקודה-שיפוע. \(y−y_{1}=m(x−x_{1})\)
- למצוא משוואה של קו מקביל לקו נתון
- מצא את השיפוע של הקו הנתון.
- מצא את שיפוע הקו המקביל.
- זהה את הנקודה.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת יירוט שיפוע.
- למצוא משוואה של קו בניצב לקו נתון
- מצא את השיפוע של הקו הנתון.
- מצא את שיפוע הקו הניצב.
- זהה את הנקודה.
- החלף את הערכים לצורת שיפוע הנקודה,. \(y−y_{1}=m(x−x_{1})\)
- כתוב את המשוואה בצורת יירוט שיפוע.
רשימת מילים
- צורת נקודה-שיפוע
- צורת הנקודה-שיפוע של משוואה של קו עם שיפוע מ"מ ומכילה את הנקודה \(\left(x_{1}, y_{1}\right)\) היא. \(y-y_{1}=m\left(x-x_{1}\right)\)


