4.4: הבנת שיפוע הקו
- Page ID
- 205738
- בסוף פרק זה, תוכל:
- השתמש בגיאובורדים כדי לדגמן שיפוע
- השתמש \(m = \frac{\text{rise}}{\text{run}}\) כדי למצוא את שיפוע הקו מהגרף שלו
- מצא את שיפוע הקווים האופקיים והאנכיים
- השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו בין שתי נקודות
- גרף קו שניתן לו נקודה והשיפוע
- לפתור יישומי שיפוע
לפני שתתחיל, קח את חידון המוכנות הזה.
- פשט:\(\frac{1 - 4}{8 - 2}\).
אם פספסת בעיה זו, עיין בתרגיל 1.6.31 - לחלק:\(\frac{0}{4}, \frac{4}{0}\).
אם פספסת בעיה זו, עיין בתרגיל 1.10.16. - פשט:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
אם פספסת בעיה זו, עיין בתרגיל 1.6.4.
כאשר אתה משרטט משוואות לינאריות, ייתכן שתבחין שחלק מהקווים נוטים כלפי מעלה כשהם עוברים משמאל לימין וחלק מהקווים נוטים כלפי מטה. חלק מהקווים תלולים מאוד וחלק מהקווים שטוחים יותר. מה קובע אם קו נוטה למעלה או למטה או אם הוא תלול או שטוח?
במתמטיקה, 'הטיה' של קו נקראת שיפוע הקו. למושג השיפוע יש יישומים רבים בעולם האמיתי. גובה הגג, דרגת הכביש המהיר ורמפה לכיסא גלגלים הם כמה דוגמאות שבהן אתה ממש רואה מדרונות. וכשאתה רוכב על אופניים, אתה מרגיש את המדרון כשאתה שואב בעלייה או בחוף בירידה.
בחלק זה נחקור את מושג השיפוע.
השתמש בגיאובורדים כדי לדגמן שיפוע
Geoboard הוא לוח עם רשת של יתדות על זה. שימוש בגומיות על גבי לוח גיאוגרפי נותן לנו דרך קונקרטית לדגמן קווים ברשת קואורדינטות. על ידי מתיחת רצועת גומי בין שני יתדות על גבי לוח גיאוגרפי, אנו יכולים לגלות כיצד למצוא את שיפוע הקו.
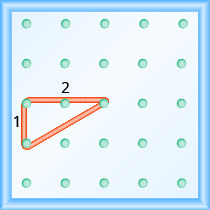
ביצוע פעילות המתמטיקה המניפולטיבית "חקר מדרון" יעזור לך לפתח הבנה טובה יותר של שיפוע הקו. (ניתן להשתמש בנייר גרף במקום לוח גיאוגרפי, במידת הצורך.)נתחיל במתיחת גומייה בין שני יתדות כמוצג באיור\(\PageIndex{1}\).
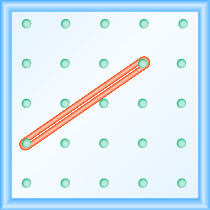
זה לא נראה כמו שורה?
כעת אנו מותחים חלק אחד של הגומייה היישר מהיתד השמאלי וסביב יתד שלישי כדי ליצור את צידי המשולש הימני, כפי שמוצג באיור \(\PageIndex{2}\)
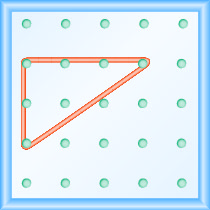
אנו מבצעים בזהירות זווית של 90 מעלות סביב יתד השלישי, כך שאחד הקווים החדשים שנוצרו הוא אנכי והשני אופקי.
כדי למצוא את שיפוע הקו, אנו מודדים את המרחק לאורך הצדדים האנכיים והאופקיים של המשולש. המרחק האנכי נקרא העלייה והמרחק האופקי נקרא הריצה, כפי שמוצג באיור\(\PageIndex{3}\).
אם הלוח הגיאוגרפי והגומי שלנו נראים בדיוק כמו זה שמוצג באיור\(\PageIndex{4}\), העלייה היא 2. רצועת הגומי עולה 2 יחידות. (כל חלל הוא יחידה אחת.)
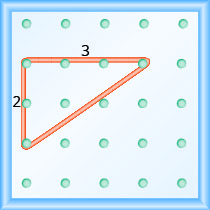
העלייה בגיאובורד זה היא 2, כאשר הגומייה עולה בשתי יחידות.
מהי הריצה?
הגומייה עוברת על פני 3 יחידות. הריצה היא 3 (ראה איור\(\PageIndex{4}\)).
שיפוע הקו הוא היחס בין העלייה לריצה. במתמטיקה, זה תמיד נקרא עם האות m.
השיפוע של קו קו הוא\(m = \frac{\text{rise}}{\text{run}}\).
העלייה מודדת את השינוי האנכי והריצה מודדת את השינוי האופקי בין שתי נקודות בקו.
מהו השיפוע של הקו על הלוח הגיאוגרפי באיור\(\PageIndex{4}\)?
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]
לקו יש שיפוע\(\frac{2}{3}\). המשמעות היא שהקו עולה 2 יחידות לכל 3 יחידות ריצה.
כאשר אנו עובדים עם geoboards, זה רעיון טוב להיכנס להרגל להתחיל ב יתד בצד שמאל ולהתחבר יתד ימינה. אם העלייה עולה היא חיובית ואם היא יורדת היא שלילית. הריצה תעבור משמאל לימין ותהיה חיובית.
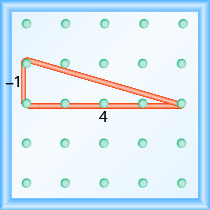
מהו שיפוע הקו על הלוח הגיאוגרפי המוצג?
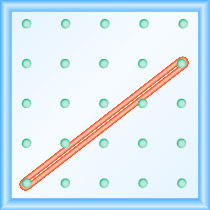
- תשובה
-
השתמש בהגדרה של שיפוע:\(m = \frac{\text{rise}}{\text{run}}\).
התחל ביתד השמאלי וספור את הרווחים למעלה ומימין כדי להגיע ליתד השני.
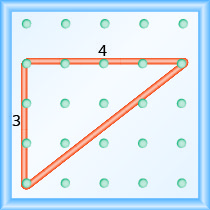
\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]
המשמעות היא שהקו עולה 3 יחידות לכל 4 יחידות ריצה.
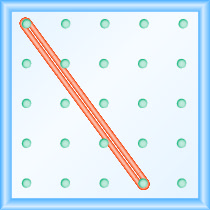
מהו שיפוע הקו על הלוח הגיאוגרפי המוצג?
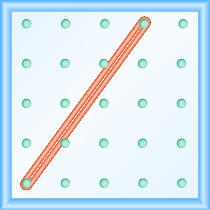
- תשובה
-
\(\frac{4}{3}\)
מהו שיפוע הקו על הלוח הגיאוגרפי המוצג?
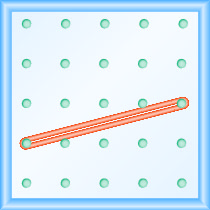
- תשובה
-
\(\frac{1}{4}\)
מהו שיפוע הקו על הלוח הגיאוגרפי המוצג?
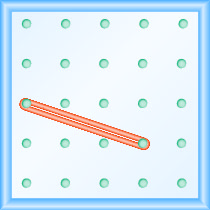
- תשובה
-
השתמש בהגדרה של שיפוע:\(m = \frac{\text{rise}}{\text{run}}\).
התחל ביתד השמאלי וספור את היחידות למטה ומימין כדי להגיע ליתד השני.
\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]
המשמעות היא שהקו יורד יחידה אחת לכל 3 יחידות ריצה.
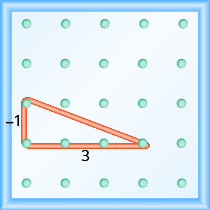
מהו המדרון של הקו על הלוח הגיאוגרפי?
- תשובה
-
\(-\frac{2}{3}\)
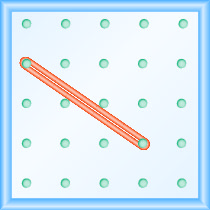
מהו המדרון של הקו על הלוח הגיאוגרפי?
- תשובה
-
\(-\frac{4}{3}\)
שימו לב \(\PageIndex{1}\) שבתרגיל השיפוע חיובי ובפעילות גופנית \(\PageIndex{4}\) המדרון שלילי. האם אתה מבחין בהבדל כלשהו בשתי השורות המוצגות באיור (א) ובאיור (ב)?
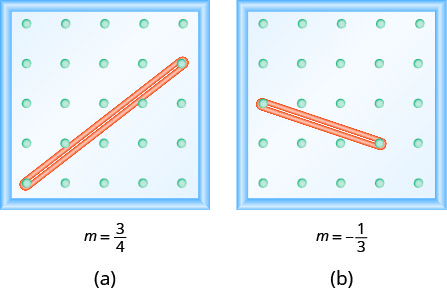
אנו 'קוראים' שורה משמאל לימין בדיוק כמו שקראנו מילים באנגלית. כשאתה קורא משמאל לימין, הקו באיור (א) עולה; יש לו שיפוע חיובי. הקו באיור (ב) יורד; יש לו שיפוע שלילי.

השתמש בגיאובורד כדי לדגמן קו עם שיפוע\(\frac{1}{2}\).
- תשובה
-
כדי לדגמן קו על לוח גיאוגרפי, אנו זקוקים לעלייה ולריצה.
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)
ההיפוטנוזה של המשולש הימני שנוצר על ידי הגומייה מייצגת קו שהשיפוע שלו הוא\(\frac{1}{2}\).
דגם את המדרון\(m = \frac{1}{3}\). צייר תמונה כדי להציג את התוצאות שלך.
- תשובה
-
דגם את המדרון\(m = \frac{3}{2}\). צייר תמונה כדי להציג את התוצאות שלך.
- תשובה
-

השתמש בגיאובורד כדי לדגמן קו עם שיפוע\(\frac{-1}{4}\).
- תשובה
-
\(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)
ההיפוטנוזה של המשולש הימני שנוצר על ידי הגומייה מייצגת קו שהשיפוע שלו הוא\(\frac{-1}{4}\).
דגם את המדרון\(m = \frac{-2}{3}\). צייר תמונה כדי להציג את התוצאות שלך.
- תשובה
-
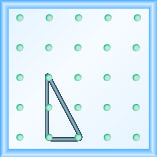
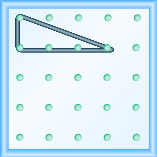
דגם את המדרון\(m = \frac{-1}{3}\). צייר תמונה כדי להציג את התוצאות שלך.
- תשובה
-
השתמש \(m = \frac{\text{rise}}{\text{run}}\) כדי למצוא את שיפוע הקו מהגרף שלו
כעת, נסתכל על כמה גרפים במישור הקואורדינטות xy ונראה כיצד למצוא את המדרונות שלהם. השיטה תהיה דומה מאוד למה שאנחנו רק דגמנו על geoboards שלנו.
כדי למצוא את המדרון, עלינו לספור את העלייה ואת הריצה. אבל מאיפה מתחילים?
אנו מאתרים שתי נקודות בקו שהקואורדינטות שלהן הן מספרים שלמים. לאחר מכן אנו מתחילים בנקודה משמאל ומשרטטים משולש ימני, כך שנוכל לספור את העלייה ולרוץ.
מצא את שיפוע הקו המוצג.
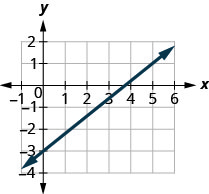
- תשובה
-

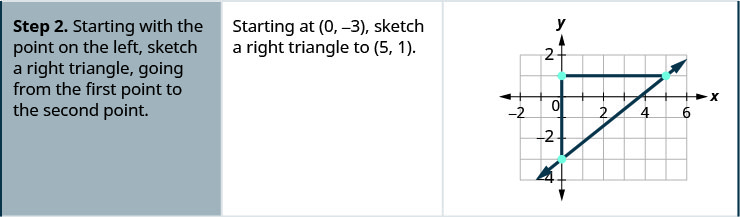


מצא את שיפוע הקו המוצג.
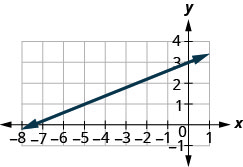
- תשובה
-
\(\frac{2}{5}\)
מצא את שיפוע הקו המוצג.
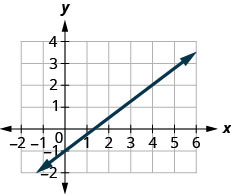
- תשובה
-
\(\frac{3}{4}\)
- אתר שתי נקודות בקו שהקואורדינטות שלהן הן מספרים שלמים.
- החל מהנקודה משמאל, שרטט משולש ימני, עובר מהנקודה הראשונה לנקודה השנייה.
- לספור את העלייה ואת הריצה על הרגליים של המשולש.
- קח את יחס העלייה לרוץ כדי למצוא את המדרון,\(m = \frac{\text{rise}}{\text{run}}\).
מצא את שיפוע הקו המוצג.
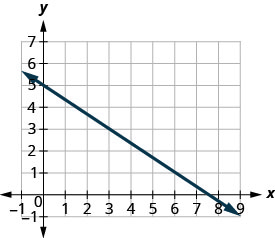
- תשובה
-
אתר שתי נקודות בגרף שהקואורדינטות שלהן הן מספרים שלמים. (0,5) ו (3,3) איזו נקודה נמצאת בצד שמאל? (0.5) החל מ (0,5), לשרטט משולש ימין (3,3). 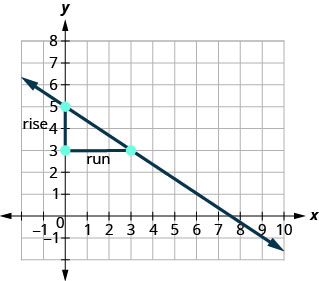
לספור את העלייה - זה שלילי. העלייה היא -2. ספור את הריצה. הריצה היא 3. השתמש בנוסחת השיפוע. \(m = \frac{\text{rise}}{\text{run}}\) החלף את ערכי העלייה והריצה. \(m = \frac{-2}{3}\) לפשט. \(m = -\frac{2}{3}\) שיפוע הקו הוא\(-\frac{2}{3}\). אז y גדל ב -3 יחידות כאשר xx יורד ב -2 יחידות.
מה אם היינו משתמשים בנקודות (-3,7) ו- (6,1) כדי למצוא את שיפוע הקו?
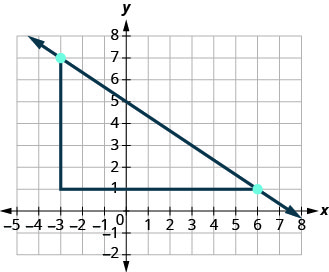
-
העלייה תהיה -6 והריצה תהיה 9. ואז\(m = \frac{-6}{9}\), וזה מפשט ל\(m = -\frac{2}{3}\). זכור, לא משנה באילו נקודות אתה משתמש - שיפוע הקו תמיד זהה.
מצא את שיפוע הקו המוצג.
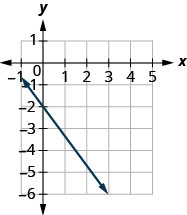
- תשובה
-
\(-\frac{4}{3}\)
מצא את שיפוע הקו המוצג.
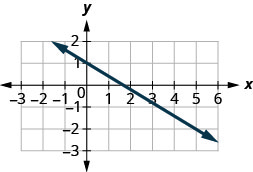
- תשובה
-
\(-\frac{3}{5}\)
בשתי הדוגמאות האחרונות, לקווים היו יירוט y עם ערכים שלמים, כך שהיה נוח להשתמש ביירוט y כאחת הנקודות כדי למצוא את המדרון. בדוגמה הבאה, יירוט y הוא שבר. במקום להשתמש בנקודה זו, נחפש שתי נקודות נוספות שהקואורדינטות שלהן הן מספרים שלמים. זה יקל על חישובי המדרון.
מצא את שיפוע הקו המוצג.

- תשובה
-
אתר שתי נקודות בגרף שהקואורדינטות שלהן הן מספרים שלמים. (2,3) ו- (7.6) איזו נקודה נמצאת בצד שמאל? (2.3) החל מ- (2,3), שרטט משולש ימני ל- (7,6). 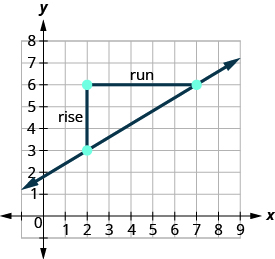
לספור את העלייה. העלייה היא 3. ספור את הריצה. הריצה היא 5. השתמש בנוסחת השיפוע. \(m = \frac{\text{rise}}{\text{run}}\) החלף את ערכי העלייה והריצה. \(m = \frac{3}{5}\) שיפוע הקו הוא\(\frac{3}{5}\). המשמעות היא ש- y מגדיל 5 יחידות כאשר x מגדיל 3 יחידות.
כאשר השתמשנו בגיאובורדים כדי להציג את מושג השיפוע, אמרנו שתמיד נתחיל בנקודה משמאל ונספור את העלייה והריצה כדי להגיע לנקודה מימין. כך הריצה תמיד הייתה חיובית והעלייה קבעה אם המדרון חיובי או שלילי.
מה היה קורה אם נתחיל בנקודה מימין?
בואו נשתמש בנקודות (2,3) ו- (7,6) שוב, אבל עכשיו נתחיל ב (7,6).
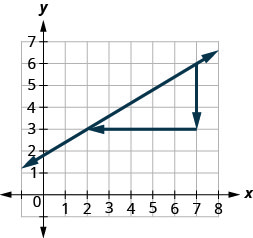
- \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
- לא משנה מאיפה מתחילים - שיפוע הקו תמיד זהה.
מצא את שיפוע הקו המוצג.
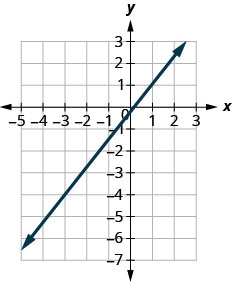
- תשובה
-
\(\frac{5}{4}\)
מצא את שיפוע הקו המוצג.
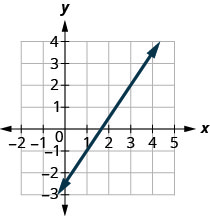
- תשובה
-
\(\frac{3}{2}\)
מצא את שיפוע הקווים האופקיים והאנכיים
אתה זוכר מה היה מיוחד בקווים אופקיים ואנכיים? למשוואות שלהם היה רק משתנה אחד.
\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]
אז איך נמצא את שיפוע הקו האופקי y = 4y = 4? גישה אחת תהיה גרף הקו האופקי, למצוא עליו שתי נקודות ולספור את העלייה והריצה. בואו נראה מה קורה כשאנחנו עושים את זה.
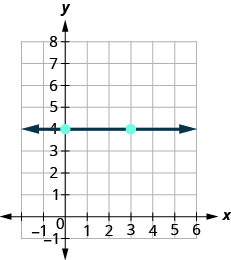
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)
לכל הקווים האופקיים יש שיפוע 0. כאשר קואורדינטות y זהות, העלייה היא 0.
השיפוע של קו אופקי, y = b, הוא 0.
רצפת החדר שלך אופקית. השיפוע שלו הוא 0. אם הנחת בזהירות כדור על הרצפה, הוא לא יתגלגל.
עכשיו, נשקול קו אנכי, הקו.
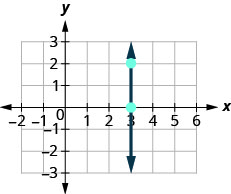
\(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)
אבל אנחנו לא יכולים לחלק ב-0. חלוקה לפי 0 אינה מוגדרת. אז אנחנו אומרים שהשיפוע של הקו האנכי איקס=3איקס=3 אינו מוגדר.
השיפוע של כל קו אנכי אינו מוגדר. כאשר הקואורדינטות x של קו זהות כולן, הריצה היא 0.
השיפוע של קו אנכי, x = a, אינו מוגדר.
מצא את השיפוע של כל שורה:
ⓐ איקס=8 ⓑ y = −5.
- תשובה
-
ⓐ x = 8
זהו קו אנכי.
השיפוע שלה אינו מוגדר.
ⓑ y=−5
זהו קו אופקי.
יש לו שיפוע 0.
מצא את שיפוע הקו: x = −4.
- תשובה
-
לא מוגדר
מצא את שיפוע הקו: y = 7.
- תשובה
-
0
זכור, אנו 'קוראים' שורה משמאל לימין, בדיוק כמו שקראנו מילים כתובות באנגלית.
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו בין שתי נקודות
ביצוע פעילות המתמטיקה המניפולטיבית "שיפוע קווים בין שתי נקודות" יעזור לך לפתח הבנה טובה יותר כיצד למצוא את שיפוע הקו בין שתי נקודות.לפעמים נצטרך למצוא את שיפוע הקו בין שתי נקודות כשאין לנו גרף לספור את העלייה והריצה. נוכל לשרטט את הנקודות על נייר רשת, ואז לספור את העלייה ואת הריצה, אבל כפי שנראה, יש דרך למצוא את המדרון ללא גרפים. לפני שנגיע לזה, עלינו להציג סימון אלגברי כלשהו.
ראינו שזוג מסודר (x, y) נותן את הקואורדינטות של נקודה. אבל כאשר אנו עובדים עם מדרונות, אנו משתמשים בשתי נקודות. כיצד ניתן להשתמש באותו סמל (x, y) לייצוג שתי נקודות שונות? מתמטיקאים משתמשים בכתבי משנה כדי להבחין בין הנקודות.
\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]
השימוש בכתבי משנה במתמטיקה דומה מאוד לשימוש בראשי תיבות של שם משפחה בבית הספר היסודי. אולי אתה זוכר את לורה סי ולורה מ 'בכיתה ג שלך?
נשתמש \(\left(x_{1}, y_{1}\right)\) כדי לזהות את הנקודה הראשונה ולזהות \(\left(x_{2}, y_{2}\right)\) את הנקודה השנייה.
אם היו לנו יותר משתי נקודות, היינו יכולים להשתמש \(\left(x_{3}, y_{3}\right)\)\(\left(x_{4}, y_{4}\right)\), וכן הלאה.
בואו נראה כיצד העלייה והריצה קשורים לקואורדינטות של שתי הנקודות על ידי התבוננות נוספת בשיפוע הקו בין הנקודות (2,3) ו- (7,6).
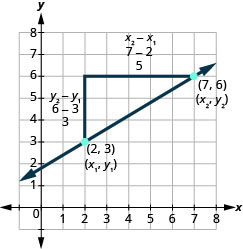
מכיוון שיש לנו שתי נקודות, נשתמש בסימון מנוי,. \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\)
בגרף ספרנו את העלייה של 3 ואת הריצה של 5.
שימו לב שניתן למצוא את העלייה של 3 על ידי חיסור ה- y -קואורדינטות 6 ו -3.
\[3=6-3\]
ואת הריצה של 5 ניתן למצוא על ידי הפחתת x -קואורדינטות 7 ו 2.
\[5 = 7 - 2\]
אנחנו יודעים\(m = \frac{\text{rise}}{\text{run}}\). אז\(m = \frac{3}{5}\).
אנו משכתבים את העלייה ורצים על ידי הכנסת הקואורדינטות \(m = \frac{6-3}{7-2}\)
אבל 6 הוא y2, ה- y -קואורדינטה של הנקודה השנייה ו- 3 הוא y1, ה- y -קואורדינטה של הנקודה הראשונה.
כך שנוכל לשכתב את המדרון באמצעות סימון תחתי. \(m = \frac{y2-y1}{7-2}\)
כמו כן, 7 הוא x2, קואורדינטת ה- x של הנקודה השנייה ו- 2 היא x1, קואורדינטת ה - x של הנקודה הראשונה.
אז, שוב, אנו משכתבים את המדרון באמצעות סימון תחתי. \(m = \frac{y2-y1}{x2-x1}\)
הראינו \(m = \frac{y2-y1}{x2-x1}\) שזו באמת גרסה אחרת של\(m = \frac{\text{rise}}{\text{run}}\). אנו יכולים להשתמש בנוסחה זו כדי למצוא את שיפוע הקו כאשר יש לנו שתי נקודות על הקו.
שיפוע הקו בין שתי נקודות \(\left(x_{1}, y_{1}\right)\) \(\left(x_{2}, y_{2}\right)\) והוא
\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]
זוהי נוסחת השיפוע.
המדרון הוא:
\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו בין הנקודות (1,2) ו- (4,5).
- תשובה
-
\(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)
בואו נאשר זאת על ידי ספירת המדרון בגרף באמצעות\(m = \frac{\text{rise}}{\text{run}}\).
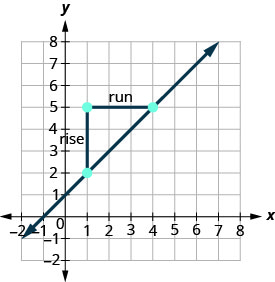
לא משנה לאיזו נקודה אתה קורא לנקודה #1 ולאיזו נקודה אתה קורא לנקודה #2. המדרון יהיה זהה. נסה את החישוב בעצמך.
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו דרך הנקודות: (8,5) ו- (6,3).
- תשובה
-
1
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו דרך הנקודות: (1,5) ו- (5,9).
- תשובה
-
1
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו דרך הנקודות (-2, -3) ו- (-7,4).
- תשובה
-
\(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)
בואו נוודא את השיפוע הזה בגרף המוצג.
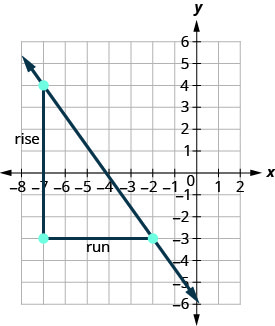
\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו דרך הנקודות: (-3,4) ו- (2, -1).
- תשובה
-
-1
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו דרך צמד הנקודות: (-2,6) ו- (-3, -4).
- תשובה
-
10
גרף קו בהינתן נקודה והשיפוע
עד כה, בפרק זה, שרטטנו קווים על ידי שרטוט נקודות, באמצעות יירוט ועל ידי זיהוי קווים אופקיים ואנכיים.
שיטה אחת נוספת בה אנו יכולים להשתמש כדי לשרטט קווים נקראת שיטת נקודה-שיפוע. אנו נשתמש בשיטה זו כאשר אנו מכירים נקודה אחת ואת שיפוע הקו. נתחיל בתכנון הנקודה ואז נשתמש בהגדרת השיפוע כדי לצייר את גרף הקו.
גרף את הקו העובר בנקודה (1, -1) שהשיפוע שלה הוא\(m = \frac{3}{4}\).
- תשובה
-




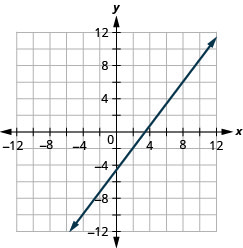
גרף את הקו העובר בנקודה (2, -2) עם המדרון\(m = \frac{4}{3}\).
- תשובה
-
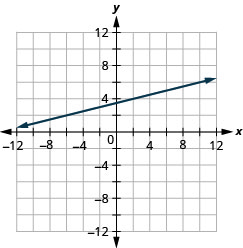
גרף את הקו העובר בנקודה (-2,3) עם השיפוע. \(m=\frac{1}{4}\)
- תשובה
-
- תכנן את הנקודה הנתונה.
- השתמש בנוסחת השיפוע \(m=\frac{\text { rise }}{\text { rise }}\) כדי לזהות את העלייה והריצה.
- החל מנקודה נתונה, לספור את העלייה ולרוץ כדי לסמן את הנקודה השנייה.
- חבר את הנקודות עם קו.
גרף את הקו עם y -intercept 2 שהשיפוע שלו הוא. \(m=−\frac{2}{3}\)
- תשובה
-
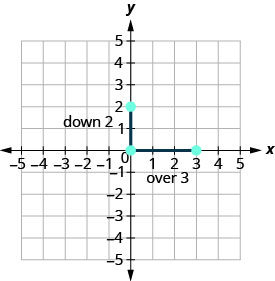
התווה את הנקודה הנתונה, ה- y -יירוט, (0,2).
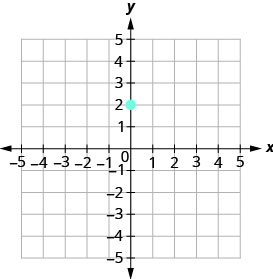
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)
לספור את העלייה ואת הריצה. סמן את הנקודה השנייה.
-
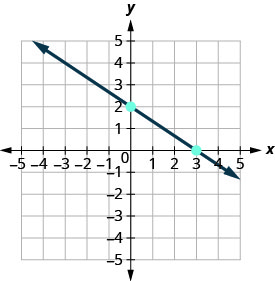
חבר את שתי הנקודות עם קו.
-
אתה יכול לבדוק את העבודה שלך על ידי מציאת נקודה שלישית. מכיוון שהמדרון הוא\(m=−\frac{2}{3}\), ניתן לכתוב אותו כ\(m=\frac{2}{-3}\). חזור אל (0,2) וספר את העלייה, 2 והריצה, -3.
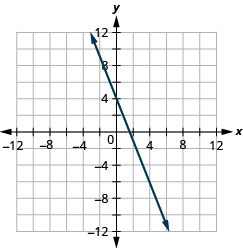
גרף את הקו עם y -יירוט 4 ושיפוע. \(m=−\frac{5}{2}\)
- תשובה
-
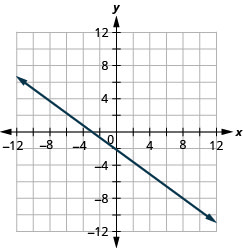
גרף את הקו עם x -יירוט -3 ושיפוע. \(m=−\frac{3}{4}\)
- תשובה
-
גרף את הקו העובר בנקודה (-1, -3) שהשיפוע שלה הוא m = 4.
- תשובה
-
תכנן את הנקודה הנתונה.
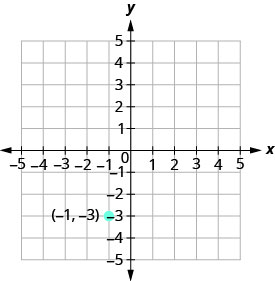
\(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)
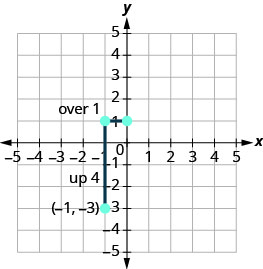
לספור את העלייה ולרוץ ולסמן את הנקודה השנייה.
-
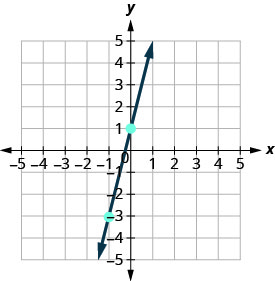
חבר את שתי הנקודות עם קו.
-
אתה יכול לבדוק את העבודה שלך על ידי מציאת נקודה שלישית. מכיוון שהשיפוע הוא m = 4, ניתן לכתוב אותו כ. \(m = \frac{-4}{-1}\) חזור אל (-1, -3) וספר את העלייה, -4, ואת הריצה, -1.
גרף את הקו עם הנקודה (-2,1) והשיפוע m = 3.
- תשובה
-
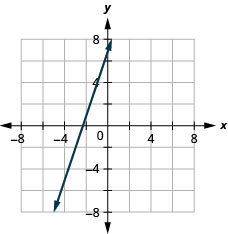
גרף את הקו עם הנקודה (4, -2) והשיפוע m = −2.
- תשובה
-
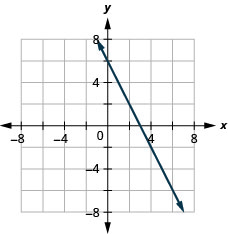
לפתור יישומי שיפוע
בתחילת פרק זה אמרנו שיש יישומים רבים של שיפוע בעולם האמיתי. בואו נסתכל על כמה עכשיו.
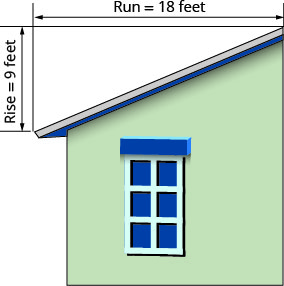
"המגרש" של גג הבניין הוא שיפוע הגג. הכרת המגרש חשובה באקלים בהם יש שלג כבד. אם הגג שטוח מדי, משקל השלג עלול לגרום לקריסתו. מהו שיפוע הגג המוצג?
- תשובה
-
\(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)
השתמש בתרגיל\(\PageIndex{40}\), החלף את העלייה = 14 ורץ = 24.
- תשובה
-
\(\frac{7}{12}\)
השתמש בתרגיל\(\PageIndex{40}\), החלף עלייה = 15 ורץ = 36.
- תשובה
-
\(\frac{5}{12}\)
האם אי פעם חשבת על צינורות הביוב שעוברים מהבית שלך לרחוב? הם חייבים להשתפל \(\frac{1}{4}\) בסנטימטר לכל רגל כדי להתנקז כראוי. מהו המדרון הנדרש?

- תשובה
-
\(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)
הצינור יורד 1 אינץ 'לכל 48 אינץ' של ריצה אופקית.
מצא את השיפוע של צינור המשתפל \(\frac{1}{3}\) בסנטימטר למטר.
- תשובה
-
\(-\frac{1}{36}\)
מצא את השיפוע של צינור המשתפל \(\frac{3}{4}\) בסנטימטר לחצר.
- תשובה
-
\(-\frac{1}{48}\)
גש למשאבים מקוונים אלה להדרכה ותרגול נוספים עם הבנת שיפוע של קו.
- תרגול שיפוע עם Geoboard וירטואלי
- גיאובורדים וירטואליים קטנים, בינוניים וגדולים
- חקור שטח והיקף עם Geoboard
מושגי מפתח
- מצא את שיפוע הקו מהגרף שלו באמצעות \(m=\frac{\text { rise }}{\text { run }}\)
- אתר שתי נקודות בקו שהקואורדינטות שלהן הן מספרים שלמים.
- החל מהנקודה משמאל, שרטט משולש ימני, עובר מהנקודה הראשונה לנקודה השנייה.
- לספור את העלייה ואת הריצה על הרגליים של המשולש.
- קח את יחס העלייה לרוץ כדי למצוא את המדרון.
- גרף קו בהינתן נקודה והשיפוע
- תכנן את הנקודה הנתונה.
- השתמש בנוסחת השיפוע \(m=\frac{\text { rise }}{\text { run }}\) כדי לזהות את העלייה והריצה.
- החל מנקודה נתונה, לספור את העלייה ולרוץ כדי לסמן את הנקודה השנייה.
- חבר את הנקודות עם קו.
- שיפוע של קו אופקי
- השיפוע של קו אופקי, y = b, הוא 0.
- שיפוע של קו אנכי
- השיפוע של קו אנכי, x = a, אינו מוגדר


