3.4: משולשים, מלבנים ומשפט פיתגורס

מטרות למידה

בסוף פרק זה, תוכל:

• לפתור יישומים באמצעות מאפיינים של משולשים
• השתמש במשפט פיתגורס
• לפתור יישומים באמצעות מאפייני מלבן

להיות מוכן

לפני שתתחיל, קח את חידון המוכנות הזה.

1. פשט:$12(6h)$.
   אם פספסת בעיה זו, עיין בתרגיל 1.10.1.
2. אורכו של מלבן הוא שלושה פחות מהרוחב. תן w לייצג את הרוחב. כתוב ביטוי לאורך המלבן.
   אם פספסת בעיה זו, סקור את תרגיל 1.3.43.
3. לפתור: $A=\frac{1}{2}bh$ עבור ב כאשר A = 260 ו- h = 52.
   אם פספסת בעיה זו, עיין בתרגיל 2.6.10.
4. פשט:$\sqrt{144}$.
   אם פספסת בעיה זו, סקור את תרגיל 1.9.10.

לפתור יישומים באמצעות מאפיינים של משולשים

בחלק זה נשתמש בכמה נוסחאות גיאומטריה נפוצות. אנו נתאים את אסטרטגיית פתרון הבעיות שלנו כך שנוכל לפתור יישומי גיאומטריה. נוסחת הגיאומטריה תקרא למשתנים ותיתן לנו את המשוואה לפתור. בנוסף, מכיוון שכל היישומים הללו יכללו צורות כלשהן, רוב האנשים מוצאים את זה מועיל לצייר דמות ולתייג אותה במידע הנתון. נכלול זאת בשלב הראשון של אסטרטגיית פתרון הבעיות ליישומי גיאומטריה.

לפתור יישומי גיאומטריה

1. קרא את הבעיה וודא שכל המילים והרעיונות מובנים. צייר את הדמות ותייג אותה במידע הנתון.
2. זהה את מה שאנחנו מחפשים.
3. תייג את מה שאנחנו מחפשים על ידי בחירת משתנה שייצג אותו.
4. תרגם למשוואה על ידי כתיבת הנוסחה או המודל המתאימים למצב. תחליף במידע הנתון.
5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
6. בדוק את התשובה על ידי החלפתה בחזרה למשוואה שנפתרה בשלב 5 ועל ידי וודא שהיא הגיונית בהקשר לבעיה.
7. ענה על השאלה במשפט שלם.

נתחיל ביישומי גיאומטריה על ידי התבוננות בתכונות המשולשים. בואו נסקור כמה עובדות בסיסיות על משולשים. למשולשים שלושה צדדים ושלוש זוויות פנים. בדרך כלל כל צד מסומן באות קטנה כדי להתאים את האות הגדולה של הקודקוד הנגדי.

רבים של המילה קודקוד הוא קודקודים. לכל המשולשים שלושה קודקודים. משולשים נקראים על ידי קודקודיהם: המשולש באיור $\PageIndex{1}$ נקרא$\triangle{ABC}$.

איור$\PageIndex{1}$: למשולש ABC יש קודקודים$A$,$B$, ו$C$. אורכי הצדדים הם$a$,$b$, ו$c$.

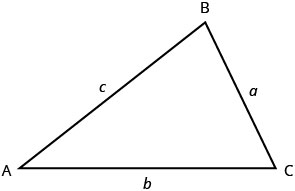
שלוש הזוויות של משולש קשורות בדרך מיוחדת. סכום האמצעים שלהם הוא$180^{\circ}$. שים לב שאנו קוראים $m\angle{A}$ כ"מדד הזווית A." אז $\triangle{ABC}$ באיור$\PageIndex{1}$.

$$m \angle A+m \angle B+m \angle C=180^{\circ} \nonumber$$

מכיוון שהיקף הדמות הוא אורך הגבול שלה, ההיקף של $\triangle{ABC}$ הוא סכום אורכי שלושת הצדדים שלה.

$$P = a + b + c \nonumber$$

כדי למצוא את שטח המשולש, עלינו לדעת את בסיסו וגובהו. הגובה הוא קו המחבר את הבסיס לקודקוד הנגדי ועושה $90^\circ$ זווית עם הבסיס. נצייר $\triangle{ABC}$ שוב, ועכשיו נראה את הגובה,$h$. ראה איור$\PageIndex{2}$.

איור$\PageIndex{2}$: הנוסחה לאזור של $\triangle{ABC}$ היא $A = \frac{1}{2}bh$ כאשר b הוא הבסיס ו - h הוא הגובה.

מאפייני משולש

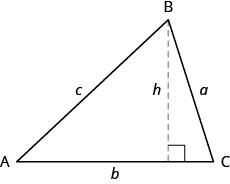
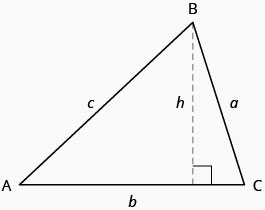
עבור $\triangle{ABC}$

מדדי זווית:

$$m \angle A+m \angle B+m \angle C=180^{\circ}$$

• סכום המידות של זוויות המשולש הוא 180 מעלות.

היקף:

$$P = a + b + c$$

• ההיקף הוא סכום אורכי צידי המשולש.

אזור:

$A = \frac{1}{2}bh, b = \text{ base }, h = \text{ height }$

• שטח המשולש הוא חצי מהבסיס כפול הגובה.

דוגמא $\PageIndex{1}$

המידות של שתי זוויות של משולש הן 55 ו 82 מעלות. מצא את מידת הזווית השלישית.

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.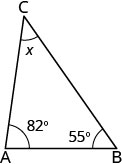
שלב 2. זהה את מה שאתה מחפש.	מידת הזווית השלישית במשולש
שלב 3. שם. בחר משתנה שייצג אותו.	תן למדוד $x=$ את הזווית.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה ותחליף.	$m \angle A+m \angle B+m \angle C=180^{\circ}$
שלב 5. לפתור את המשוואה.	$\begin{array} {rll} {55 + 82 + x} &{=} &{180} \\ {137 + x} &{=} &{180} \\ {x} &{=} &{43} \end{array}$
שלב 6. בדוק. $\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}$
שלב 7. תענה על השאלה.	מידת הזווית השלישית היא 43 מעלות.

נסה את זה $\PageIndex{1}$

המידות של שתי זוויות של משולש הן 31 ו 128 מעלות. מצא את מידת הזווית השלישית.

תשובה

21 מעלות

נסה את זה $\PageIndex{2}$

המידות של שתי זוויות של משולש הן 49 ו 75 מעלות. מצא את מידת הזווית השלישית.

תשובה

56 מעלות

דוגמא $\PageIndex{2}$

ההיקף של גן משולש הוא 24 רגל. אורכם של שני הצדדים הם ארבעה מטרים ותשעה רגל. כמה זמן הוא הצד השלישי?

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.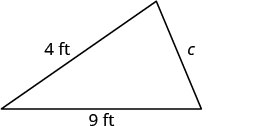
שלב 2. זהה את מה שאתה מחפש.	אורך הצד השלישי של משולש
שלב 3. שם. בחר משתנה שייצג אותו.	תן $c=$ את הצד השלישי.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה ותחליף.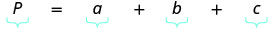
תחליף במידע הנתון.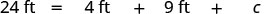
שלב 5. לפתור את המשוואה.
שלב 6. בדוק. $\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11} \\ {24} &{=} &{24\checkmark} \end{array}$
שלב 7. תענה על השאלה.	אורכו של הצד השלישי הוא 11 רגל.

נסה את זה $\PageIndex{3}$

ההיקף של גן משולש הוא 48 רגל. אורכם של שני הצדדים הם 18 רגל ו -22 רגל. כמה זמן הוא הצד השלישי?

תשובה

8 רגל

נסה את זה $\PageIndex{4}$

אורכם של שני צדדים של חלון משולש הם שבעה מטרים וחמישה מטרים. ההיקף הוא 18 רגל. כמה זמן הוא הצד השלישי?

תשובה

6 רגל

דוגמא $\PageIndex{3}$

שטח חלון הכנסייה המשולש הוא 90 מ"ר. בסיס החלון הוא 15 מטר. מה גובה החלון?

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.	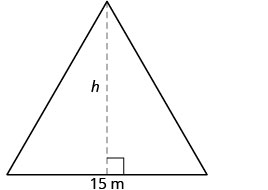$\text{ Area } = 90m^{2}$
שלב 2. זהה את מה שאתה מחפש.	גובה המשולש
שלב 3. שם. בחר משתנה שייצג אותו.	תן $h=$ לגובה.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה.
תחליף במידע הנתון.
שלב 5. לפתור את המשוואה.	$90 = \dfrac{15}{2}h$ $12 = h$
שלב 6. בדוק. $\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}$
שלב 7. תענה על השאלה.	גובה המשולש הוא 12 מטר.

נסה את זה $\PageIndex{5}$

שטחו של ציור משולש הוא 126 אינץ 'מרובע. הבסיס הוא 18 אינץ '. מהו הגובה?

תשובה

14 אינץ '

נסה את זה $\PageIndex{6}$

דלת אוהל משולשת כוללת שטח של 15 רגל מרובע. הגובה הוא מטר וחצי. מהו הבסיס?

תשובה

6 רגל

מאפייני המשולש בהם השתמשנו עד כה חלים על כל המשולשים. כעת נבחן סוג מסוים של משולש - משולש ימני. למשולש ימני יש זווית אחת של 90 מעלות, אותה אנו מסמנים בדרך כלל בריבוע קטן בפינה.

איור $\PageIndex{3}$

הגדרה: משולש ימני

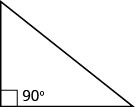
למשולש ימני יש זווית אחת של 90 מעלות, המסומנת לרוב בריבוע בקודקוד.

דוגמא $\PageIndex{4}$

זווית אחת של משולש ימני נמדדת 28°. מהו המדד של הזווית השלישית?

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.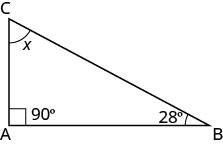
שלב 2. זהה את מה שאתה מחפש.	מידת הזווית
שלב 3. שם. בחר משתנה שייצג אותו.	$x=$תן למדוד זווית.
שלב 4. תרגם.	$m\angle{A} + m\angle{B} + m\angle{C} = 180$
כתוב את הנוסחה המתאימה ותחליף.	$x+90+28=180$
שלב 5. לפתור את המשוואה.	$x=62$
שלב 6. בדוק. $\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \end{array}$
שלב 7. תענה על השאלה.	מידת הזווית השלישית היא 62 ^°.

נסה את זה $\PageIndex{7}$

זווית אחת של משולש ימני מודדת 56°. מהו המדד של הזווית הקטנה האחרת?

תשובה

34°

נסה את זה $\PageIndex{8}$

זווית אחת של משולש ימני נמדדת 45°. מהו המדד של הזווית הקטנה האחרת?

תשובה

45°

בדוגמאות שראינו עד כה נוכל לצייר דמות ולתייג אותה ישירות לאחר קריאת הבעיה. בדוגמה הבאה נצטרך להגדיר זווית אחת במונחים של זווית אחרת. נחכה לצייר את הדמות עד שנכתוב ביטויים לכל הזוויות שאנו מחפשים.

דוגמא $\PageIndex{5}$

המדד של זווית אחת של משולש ימין הוא 20 מעלות יותר מאשר המדד של הזווית הקטנה ביותר. מצא את המידות של שלוש הזוויות.

פתרון

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	המידות של כל שלוש הזוויות
שלב 3. שם. בחר משתנה שייצג אותו.	תן $a=1^{st}$ זווית. $a+20=2^{nd}$זווית $90=3^{rd}$ זווית (הזווית הנכונה)
צייר את הדמות ותייג אותה במידע הנתון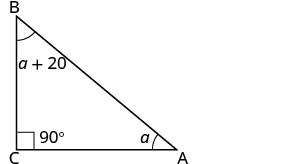
שלב 4. תרגם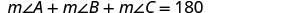
כתוב את הנוסחה המתאימה. תחליף לתוך הנוסחה.	$a + (a + 20) + 90 = 180$
שלב 5. לפתור את המשוואה.	\ (\ התחל {יישור*} 2a + 110 &= 180\\ [3pt] 2a &= 70\\ [3pt] a &= 35\ טקסט {זווית ראשונה}\\\ [3pt] a &+ 20\ טקסט {זווית שנייה}\\\ [3pt] {\ צבע {אדום} {35}} &+ 20 = 55\ סוף {יישור*}\) והזווית השלישית היא 90.
שלב 6. בדוק. $\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}$
שלב 7. תענה על השאלה.	שלוש הזוויות נמדדות 35 ^°, 55 ^° ו- 90 ^°.

נסה את זה $\PageIndex{9}$

המידה של זווית אחת של משולש ימני היא 50 מעלות יותר ממדידת הזווית הקטנה ביותר. מצא את המידות של שלוש הזוויות.

תשובה

20°, 70°, 90°

נסה את זה $\PageIndex{10}$

המידה של זווית אחת של משולש ימני היא 30 מעלות יותר ממדידת הזווית הקטנה ביותר. מצא את המידות של שלוש הזוויות.

תשובה

30°, 60°, 90°

השתמש במשפט פיתגורס

למדנו כיצד מדדי הזוויות של משולש קשורים זה לזה. כעת נלמד כיצד אורכי הצדדים קשורים זה לזה. מאפיין חשוב המתאר את הקשר בין אורכי שלושת הצדדים של משולש ימין נקרא משפט פיתגורס. משפט זה שימש ברחבי העולם מאז ימי קדם. הוא נקרא על שם הפילוסוף והמתמטיקאי היווני, פיתגורס, שחי בסביבות 500 לפני הספירה.

לפני שנציין את משפט פיתגורס, עלינו להציג כמה מונחים לצידי המשולש. זכור כי למשולש ימני יש זווית של 90 מעלות, המסומנת בריבוע קטן בפינה. הצד של המשולש מול זווית 90° 90° נקרא hypotenuse וכל אחד מהצדדים האחרים נקרא רגליים.

איור $\PageIndex{4}$

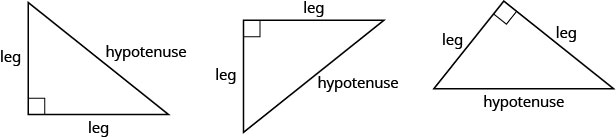
משפט פיתגורס מספר כיצד אורכי שלושת הצדדים של משולש ימין קשורים זה לזה. הוא קובע כי בכל משולש ימני, סכום הריבועים באורכי שתי הרגליים שווה לריבוע אורך ההיפוטנוזה. בסמלים אנו אומרים: בכל משולש ימני,$a^{2}+b^{2}=c^{2}$, כאשר a ו- b הם אורכי הרגליים ו- cc הוא אורך ההיפוטנוזה.

כתיבת הנוסחה בכל תרגיל ואמירה בקול רם בזמן שאתה כותב אותה, עשויה לעזור לך לזכור את משפט פיתגורס.

משפט פיתגורס

בכל משולש ימני, $b$ היכן $a$ ואורכי הרגליים, $c$ נמצא אורך ההיפוטנוזה.

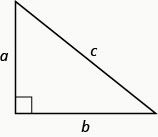
ואז

$$a^{2}+b^{2}=c^{2} \label{Ptheorem}$$

כדי לפתור תרגילים המשתמשים במשפט פיתגורס (משוואה\ ref {Ptheorm}), נצטרך למצוא שורשים מרובעים. השתמשנו בסימון $\sqrt{m}$ ובהגדרה:

אם$m = n^{2}$, אז$\sqrt{m} = n$, עבור$n\geq 0$.

לדוגמה, מצאנו כי $\sqrt{25}$ הוא 5 כי$25=5^{2}$.

מכיוון שמשפט פיתגורס מכיל משתנים בריבוע, כדי לפתור את אורך הצד במשולש ימני, נצטרך להשתמש בשורשים מרובעים.

דוגמא $\PageIndex{6}$

השתמש במשפט פיתגורס כדי למצוא את אורך ההיפוטנוזה המוצגת להלן.

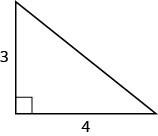
פתרון

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	אורך ההיפוטנוזה של המשולש
שלב 3. שם. בחר משתנה שייצג אותו. תווית בצד c על הדמות.	תן ג = אורך ההיפוטנוזה.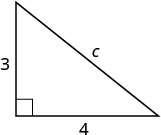
שלב 4. תרגם.
כתוב את הנוסחה המתאימה.	$a^{2} + b^{2} = c^{2}$
תחליף.	$3^{2}+4^{2}=c^{2}$
שלב 5. לפתור את המשוואה.	$9+16=c^{2}$
לפשט.	$25=c^{2}$
השתמש בהגדרה של שורש ריבועי.	$\sqrt{25} = c$
לפשט.	$5=c$
שלב 6. בדוק.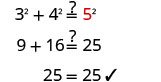
שלב 7. תענה על השאלה.	אורך ההיפוטנוזה הוא 5.

נסה את זה $\PageIndex{11}$

השתמש במשפט פיתגורס כדי למצוא את אורך ההיפוטנוזה במשולש המוצג להלן.

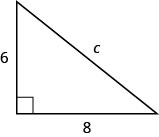
תשובה

c=10

נסה את זה $\PageIndex{12}$

השתמש במשפט פיתגורס כדי למצוא את אורך ההיפוטנוזה במשולש המוצג להלן.

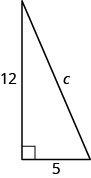
תשובה

c=13

דוגמא $\PageIndex{7}$

השתמש במשפט פיתגורס כדי למצוא את אורך הרגל המוצג להלן.

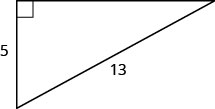
פתרון

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	אורך הרגל של המשולש
שלב 3. שם. בחר משתנה שייצג אותו.	תן $b=$ את הרגל של המשולש.
צד התווית$b$.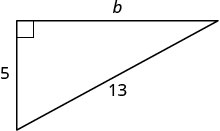
שלב 4. תרגם
כתוב את הנוסחה המתאימה.	$a^{2} + b^{2} = c^{2}$
תחליף.	$5^{2}+b^{2}=13^{2}$
שלב 5. לפתור את המשוואה.	$25+b^{2}=169$
לבודד את המונח המשתנה.	$b^{2}=144$
השתמש בהגדרה של שורש ריבועי.	$b = \sqrt{144}$
לפשט.	$b=12$
שלב 6. בדוק.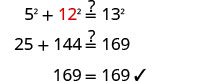
שלב 7. תענה על השאלה.	אורך הרגל הוא 12.

נסה את זה $\PageIndex{13}$

השתמש במשפט פיתגורס כדי למצוא את אורך הרגל במשולש המוצג להלן.

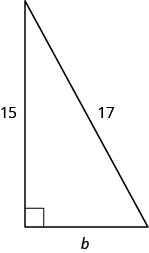
תשובה

8

נסה את זה $\PageIndex{14}$

השתמש במשפט פיתגורס כדי למצוא את אורך הרגל במשולש המוצג להלן.

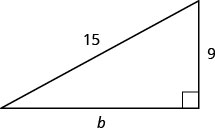
תשובה

12

דוגמא $\PageIndex{8}$

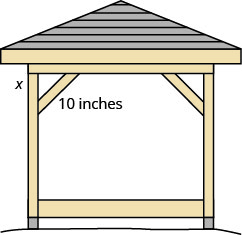
קלווין בונה ביתן ורוצה לסד כל פינה על ידי הנחת פיסת עץ בגודל 10 אינץ 'באלכסון כמוצג לעיל.

אם הוא מהדק את העץ כך שקצות הסד יהיו באותו מרחק מהפינה, מה אורך רגלי המשולש הימני שנוצר? משוער לעשירית הסנטימטר הקרובה ביותר.

פתרון

$\begin{array} {ll} {\textbf{Step 1. }\text{Read the problem.}} &{} \\\\ {\textbf{Step 2. }\text{Identify what we are looking for.}} &{\text{the distance from the corner that the}} \\ {} &{\text{bracket should be attached}} \\ \\{\textbf{Step 3. }\text{Name. Choose a variable to represent it.}} &{\text{Let x = distance from the corner.}} \\ {\textbf{Step 4.} \text{Translate}} &{} \\ {\text{Write the appropriate formula and substitute.}} &{a^{2} + b^{2} = c^{2}} \\ {} &{x^{2} + x^{2} = 10^{2}} \\ \\ {\textbf{Step 5. Solve the equation.}} &{} \\ {} &{2x^{2} = 100} \\ {\text{Isolate the variable.}} &{x^{2} = 50} \\ {\text{Simplify. Approximate to the nearest tenth.}} &{x \approx 7.1}\\\\ {\textbf{Step 6. }\text{Check.}} &{}\\ {a^{2} + b^{2} = c^{2}} &{} \\ {(7.1)^{2} + (7.1)^{2} \approx 10^{2} \text{ Yes.}} &{} \\\\ {\textbf{Step 7. Answer the question.}} &{\text{Kelven should fasten each piece of}} \\ {} &{\text{wood approximately 7.1'' from the corner.}} \end{array}$

נסה את זה $\PageIndex{15}$

ג'ון מניח את בסיס סולם בגודל 13 רגל חמישה מטרים מקיר ביתו כפי שמוצג להלן. כמה רחוק במעלה הקיר מגיע הסולם?

תשובה

12 רגל

נסה את זה $\PageIndex{16}$

רנדי רוצה לחבר מחרוזת אורות בגובה 17 רגל לראש התורן בגובה 15 רגל של סירת המפרש שלו, כפי שמוצג להלן. כמה רחוק מבסיס התורן עליו לחבר את קצה החוט הקל?

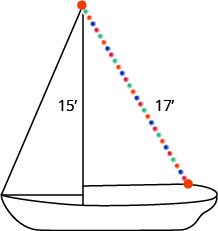
תשובה

8 רגל

לפתור יישומים באמצעות מאפייני מלבן

יתכן שאתה כבר מכיר את המאפיינים של מלבנים. למלבנים ארבעה צדדים וארבע זוויות ימניות (90°). הצדדים הנגדיים של מלבן הם באותו אורך. אנו מתייחסים לצד אחד של המלבן כאורך,$L$, והצד הסמוך שלו כרוחב,$W$.

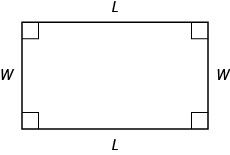
המרחק סביב מלבן זה הוא$L+W+L+W$, או$2L+2W$. זהו ההיקף,$P$, של המלבן.

$$P=2L+2W$$

מה לגבי שטח המלבן? דמיין שטיח מלבני שאורכו 2 מטר על רוחב 3 מטר. שטחו הוא 6 מטרים רבועים. יש שישה ריבועים באיור.

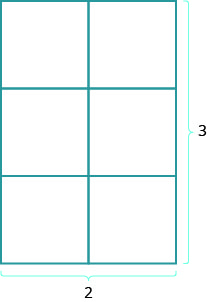
$$\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}$$

האזור הוא האורך כפול הרוחב. הנוסחה לאזור המלבן היא

$$A=LW.$$

מאפיינים של מלבנים

למלבנים ארבעה צדדים וארבע זוויות ימניות (90°).

אורכי הצדדים המנוגדים שווים.

היקף המלבן הוא סכום כפול מהאורך ופעמיים הרוחב.

$$P=2L+2W$$

שטח המלבן הוא תוצר האורך והרוחב.

$$A=L·W$$

דוגמא $\PageIndex{9}$

אורכו של מלבן הוא 32 מטר והרוחב הוא 20 מטר. מהו ההיקף?

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.
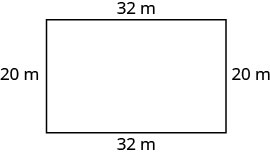שלב 2. זהה את מה שאתה מחפש.	ההיקף של מלבן
שלב 3. שם. בחר משתנה שייצג אותו.	תן $P=$ את ההיקף.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה.
תחליף.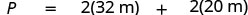
שלב 5. לפתור את המשוואה.	$P = 64 + 40$ $P = 104$
שלב 6. בדוק. $\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{=}} &{104} \\ {104} &{=} &{104\checkmark} \end{array}$
שלב 7. תענה על השאלה.	היקף המלבן הוא 104 מטר.

נסה את זה $\PageIndex{17}$

אורכו של מלבן הוא 120 מטר והרוחב הוא 50 מטר. מהו ההיקף?

תשובה

340 יארד

נסה את זה $\PageIndex{18}$

אורכו של מלבן הוא 62 רגל והרוחב 48 רגל. מהו ההיקף?

תשובה

220 רגל

דוגמא $\PageIndex{10}$

שטחו של חדר מלבני הוא 168 מטרים רבועים. האורך הוא 14 רגל. מהו הרוחב?

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.
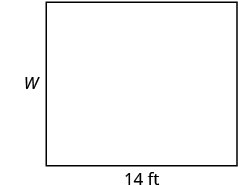שלב 2. זהה את מה שאתה מחפש.	רוחבו של חדר מלבני
שלב 3. שם. בחר משתנה שייצג אותו.	תן $W=$ לרוחב.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה.	$A=LW$
תחליף.	$168 = 14W$
שלב 5. לפתור את המשוואה.	$\frac{168}{14} = \frac{14W}{14}$ $12 = W$
שלב 6. בדוק. 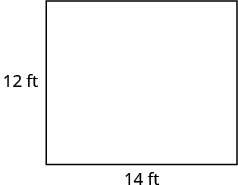$\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ {168} &{=} &{168\checkmark} \end{array}$
שלב 7. תענה על השאלה.	רוחב החדר הוא 12 רגל.

נסה את זה $\PageIndex{19}$

שטח המלבן הוא 598 רגל מרובע. האורך הוא 23 רגל. מהו הרוחב?

תשובה

26 רגל

נסה את זה $\PageIndex{20}$

רוחב המלבן הוא 21 מטר. השטח הוא 609 מטרים רבועים. מהו האורך?

תשובה

29 מטר

דוגמא $\PageIndex{11}$

מצא את אורך המלבן עם היקף 50 אינץ 'ורוחב 10 אינץ'.

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.
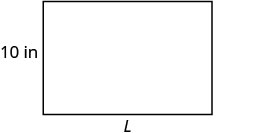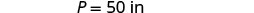שלב 2. זהה את מה שאתה מחפש.	אורכו של המלבן
שלב 3. שם. בחר משתנה שייצג אותו.	תן $L=$ את האורך.
שלב 4. תרגם.
כתוב את הנוסחה המתאימה.	$P = 2L + 2W$
תחליף.	$50 = 2L + 2(10)$
שלב 5. לפתור את המשוואה.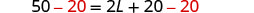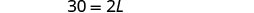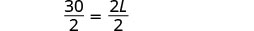
שלב 6. בדוק. $\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{array}$
שלב 7. תענה על השאלה.	האורך הוא 15 אינץ '.

נסה את זה $\PageIndex{21}$

מצא את אורך המלבן עם: היקף 80 ורוחב 25.

תשובה

15

נסה את זה $\PageIndex{22}$

מצא את אורך המלבן עם: היקף 30 ורוחב 6.

תשובה

9

פתרנו בעיות בהן ניתן האורך או הרוחב, יחד עם ההיקף או השטח; כעת נלמד כיצד לפתור בעיות בהן הרוחב מוגדר מבחינת האורך. נחכה לצייר את הדמות עד שנכתוב ביטוי לרוחב כדי שנוכל לתייג צד אחד בביטוי זה.

דוגמא $\PageIndex{12}$

רוחב המלבן הוא שני מטרים פחות מהאורך. ההיקף הוא 52 רגל. מצא את האורך והרוחב.

פתרון

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	האורך והרוחב של מלבן
שלב 3. שם. בחר משתנה שייצג אותו. מכיוון שהרוחב מוגדר מבחינת האורך, אנו נותנים $L=$ לאורך. הרוחב הוא שני מטרים פחות מהאורך, ולכן אנו נותנים $L-2$ לרוחב.	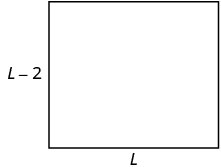$P=52$ft
שלב 4. תרגם.
כתוב את הנוסחה המתאימה. הנוסחה להיקף המלבן מתייחסת לכל המידע.	$P=2L+2W$
תחליף במידע הנתון.	$52=2L+2(L−2)$
שלב 5. לפתור את המשוואה.	$52=2L+2L−4$
לשלב מונחים כמו.	$52=4L−4$
הוסף 4 לכל צד.	$56 = 4L$
מחלקים ב -4.	$\frac{56}{4} = \frac{4L}{4}$ $14=L$ האורך הוא 14 רגל.
עכשיו אנחנו צריכים למצוא את הרוחב.	הרוחב הוא$L−2$. הרוחב הוא 12 רגל.
שלב 6. בדוק. מאז$14+12+14+12=52$, זה עובד!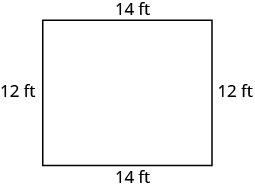
שלב 7. תענה על השאלה.	האורך הוא 14 רגל והרוחב הוא 12 רגל.

נסה את זה $\PageIndex{23}$

רוחב המלבן הוא שבעה מטרים פחות מהאורך. ההיקף הוא 58 מטר. מצא את האורך והרוחב.

תשובה

18 מטר, 11 מטר

נסה את זה $\PageIndex{24}$

אורכו של מלבן הוא שמונה מטרים יותר מהרוחב. ההיקף הוא 60 רגל. מצא את האורך והרוחב.

תשובה

19 רגל, 11 רגל

דוגמא $\PageIndex{13}$

אורכו של מלבן הוא ארבעה סנטימטרים יותר מכפליים מהרוחב. ההיקף הוא 32 ס"מ. מצא את האורך והרוחב.

פתרון

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאתה מחפש.	האורך והרוחב
שלב 3. שם. בחר משתנה שייצג את הרוחב.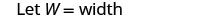
האורך הוא ארבעה יותר מפי שניים מהרוחב.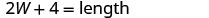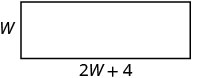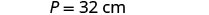
שלב 4. תרגם
כתוב את הנוסחה המתאימה.	$\quad P=2L+2W$
תחליף במידע הנתון.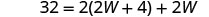
שלב 5. לפתור את המשוואה.	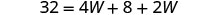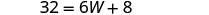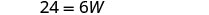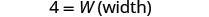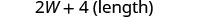12 האורך הוא 12 ס"מ.
שלב 6. בדוק. 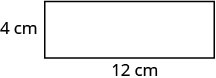$\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2\cdot 4} \\ {32} &{=} &{32\checkmark} \end{array}$
שלב 7. תענה על השאלה.	האורך הוא 12 ס"מ והרוחב הוא 4 ס"מ.

נסה את זה $\PageIndex{25}$

אורכו של מלבן הוא שמונה יותר מפי שניים מהרוחב. ההיקף הוא 64. מצא את האורך והרוחב.

תשובה

24, 8

נסה את זה $\PageIndex{26}$

רוחב המלבן הוא שש פחות מפי שניים מהאורך. ההיקף הוא 18. מצא את האורך והרוחב.

תשובה

5, 4

דוגמא $\PageIndex{14}$

ההיקף של בריכת שחייה מלבנית הוא 150 מטרים. האורך הוא 15 רגל יותר מהרוחב. מצא את האורך והרוחב.

פתרון

שלב 1. קרא את הבעיה. צייר את הדמות ותייג אותה במידע הנתון.	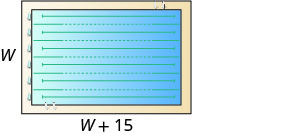$P=150$ft
שלב 2. זהה את מה שאתה מחפש.	האורך והרוחב של הבריכה
שלב 3. שם. בחר משתנה שייצג את הרוחב. האורך הוא 15 רגל יותר מהרוחב.
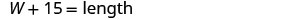שלב 4. תרגם
כתוב את הנוסחה המתאימה.	$\quad P=2L+2W$
תחליף.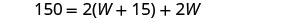
שלב 5. לפתור את המשוואה.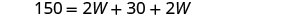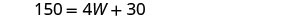
שלב 6. בדוק. $\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}$
שלב 7. תענה על השאלה.	אורך הבריכה 45 רגל והרוחב הוא 30 רגל.

נסה את זה $\PageIndex{27}$

ההיקף של בריכת שחייה מלבנית הוא 200 מטרים. האורך הוא 40 רגל יותר מהרוחב. מצא את האורך והרוחב.

תשובה

70 רגל, 30 רגל

נסה את זה $\PageIndex{28}$

אורכו של גינה מלבנית הוא 30 מטר יותר מהרוחב. ההיקף הוא 300 מטרים. מצא את האורך והרוחב.

תשובה

90 יארד, 60 יארד

מושגי מפתח

• אסטרטגיה לפתרון בעיות ליישומי גיאומטריה
  1. קרא את הבעיה וגרם להבנה של כל המילים והרעיונות. צייר את הדמות ותייג אותה במידע הנתון.
  2. זהה את מה שאנחנו מחפשים.
  3. תן שם למה שאנחנו מחפשים על ידי בחירת משתנה שייצג אותו.
  4. תרגם למשוואה על ידי כתיבת הנוסחה או המודל המתאימים למצב. תחליף במידע הנתון.
  5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
  6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
  7. ענה על השאלה במשפט שלם.
• מאפייני משולש עבור מדדי
  זווית ABC:
  • $m\angle{A}+m\angle{B}+m\angle{C}=180$
  היקף:
  • $P=a+b+c$
  אזור:
  • $A=\frac{1}{2}bh$, b = בסיס, h = גובה
  למשולש ימני יש זווית אחת של 90 מעלות.
• משפט פיתגורס בכל משולש ימני, $a^{2} + b^{2} = c^{2}$ $c$ היכן אורך ההיפוטנוזה $a$ $b$ והם אורכי הרגליים.
• מאפיינים של מלבנים
  • למלבנים ארבעה צדדים וארבע זוויות ימניות (90°).
  • אורכי הצדדים המנוגדים שווים.
  • היקף המלבן הוא סכום של פי שניים מהאורך ופעמיים הרוחב:$P=2L+2W$.
  • השטח של מלבן הוא האורך כפול הרוחב:$A=LW$.