3.3: לפתור יישומי תערובת

מטרות למידה

בסוף פרק זה תוכל:

• לפתור בעיות של מילות מטבע
• לפתור בעיות של כרטיסים ומילות חותמת
• לפתור בעיות של מילות תערובת
• השתמש במודל התערובת כדי לפתור בעיות השקעה באמצעות ריבית פשוטה

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

1. הכפל:$14(0.25)$.
   אם פספסת בעיה זו, סקור את תרגיל 1.8.19.
2. לפתור:$0.25x+0.10(x+4)=2.5$.
   אם פספסת בעיה זו, עיין בתרגיל 2.4.22.
3. מספר הפרוטות הוא שלושה יותר ממספר הרבעונים. תן q לייצג את מספר הרבעונים. כתוב ביטוי למספר הפרוטות.
   אם פספסת בעיה זו, סקור את תרגיל 1.3.43.

לפתור בעיות של מילות מטבע

בבעיות תערובת, יהיו לנו שני פריטים או יותר עם ערכים שונים לשילוב יחד. מודל התערובת משמש את המכולת והברמנים כדי לוודא שהם קובעים מחירים הוגנים עבור המוצרים שהם מוכרים. אנשי מקצוע רבים אחרים, כמו כימאים, בנקאי השקעות ומעצבי נוף משתמשים גם במודל התערובת.

הערה

ביצוע פעילות המתמטיקה המניפולטיבית Coin Lab יעזור לך לפתח הבנה טובה יותר של בעיות מילות תערובת.

נתחיל בהסתכלות על יישום שכולם מכירים - כסף!

תארו לעצמכם שאנחנו לוקחים קומץ מטבעות מכיס או ארנק ומניחים אותם על שולחן. איך היינו קובעים את הערך של ערימת המטבעות? אם נוכל ליצור תוכנית שלב אחר שלב למציאת הערך הכולל של המטבעות, זה יעזור לנו כשאנחנו מתחילים לפתור בעיות של מילות מטבע.

אז מה היינו עושים? כדי לקבל קצת סדר בבלגן המטבעות, נוכל להפריד את המטבעות לערימות לפי ערכם. רבעים היו הולכים עם רבעים, אגורות עם פרוטות, ניקל עם ניקל וכן הלאה. כדי לקבל את הערך הכולל של כל המטבעות, נוסיף את הערך הכולל של כל ערימה.

איור $\PageIndex{1}$

כיצד נקבע הערך של כל ערימה? חשבו על ערימת הפרוטות - כמה היא שווה? אם נספור את מספר הפרוטות, נדע כמה יש לנו - מספר הפרוטות.

אבל זה לא אומר לנו את הערך של כל הפרוטות. נגיד שספרנו 17 אגורות, כמה הם שווים? כל אגורה שווה 0.10$ - זה הערך של אגורה אחת. כדי למצוא את הערך הכולל של ערימת 17 אגורות, הכפל 17 ב- $0.10 כדי לקבל 1.70$. זהו הערך הכולל של כל 17 הפרוטות. שיטה זו מובילה למודל הבא.

ערך כולל של מטבעות

עבור אותו סוג של מטבע, הערך הכולל של מספר מטבעות נמצא באמצעות המודל

$$number\cdot value = total\space value$$

כאשר
המספר הוא מספר המטבעות

הערך הוא הערך של כל מטבע

הערך הכולל הוא הערך הכולל של כל המטבעות

מספר הפרוטות כפול הערך של כל אגורה שווה לערך הכולל של הפרוטות.

$$\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}$$

נוכל להמשיך בתהליך זה עבור כל סוג מטבע, ואז נדע את הערך הכולל של כל סוג מטבע. כדי לקבל את הערך הכולל של כל המטבעות, להוסיף את הערך הכולל של כל סוג של מטבע.

בואו נסתכל על מקרה ספציפי. נניח שיש 14 רבעים, 17 אגורות, 21 ניקל ו -39 פרוטות.

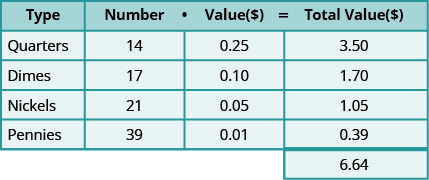
טבלה $\PageIndex{1}$

הערך הכולל של כל המטבעות הוא 6.64$.

שימו לב כיצד התרשים עוזר לארגן את כל המידע! בואו נראה כיצד אנו משתמשים בשיטה זו כדי לפתור בעיה של מילות מטבע.

דוגמא $\PageIndex{1}$

לאדלברטו יש 2.25 דולר בפרוטות וניקלים בכיס. יש לו תשעה אגורות יותר ממטבעות. כמה מכל סוג מטבע יש לו?

פתרון

שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.

קבע את סוגי המטבעות המעורבים.
חשבו על האסטרטגיה בה השתמשנו כדי למצוא את הערך של קומץ המטבעות. הדבר הראשון שאנחנו צריכים זה לשים לב אילו סוגים של מטבעות מעורבים. לאדלברטו יש מטבעות וניקלים. צור טבלה לארגון המידע. ראה תרשים למטה.

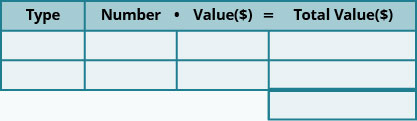
• תייג את העמודות "סוג", "מספר", "ערך", "ערך כולל".
• רשום את סוגי המטבעות.
• כתוב את הערך של כל סוג של מטבע.
• כתוב את הערך הכולל של כל המטבעות.

אנחנו יכולים לפתור את הבעיה הזו בסנטים או בדולרים. כאן נעשה את זה בדולרים ונכניס את סימן הדולר ($) בטבלה כתזכורת.
הערך של אגורה הוא 0.10$ והערך של ניקל הוא 0.05$. הערך הכולל של כל המטבעות הוא 2.25$. הטבלה שלהלן מציגה מידע זה.

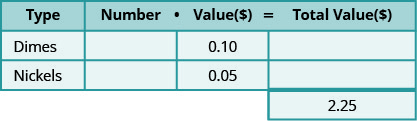
שלב 2. זהה את מה שאנחנו מחפשים.

אנו מתבקשים למצוא את מספר הפרוטות והניקל שיש לאדלברטו.

שלב 3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.

השתמש בביטויים משתנים כדי לייצג את המספר של כל סוג מטבע ולכתוב אותם בטבלה.

הכפל את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג מטבע.

בשלב הבא ספרנו את המספר של כל סוג מטבע. בבעיה זו איננו יכולים לספור כל סוג של מטבע - זה מה שאתה מחפש - אך יש לנו מושג. יש תשעה אגורות יותר ממטבעות. מספר הניקלים הוא תשעה יותר ממספר הפרוטות.

$$\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}$$

מלא את העמודה "מספר" בטבלה כדי לעזור לארגן את הכל.

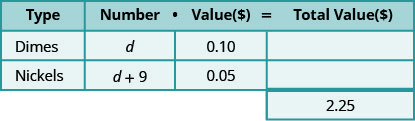
עכשיו יש לנו את כל המידע שאנחנו צריכים מהבעיה!

אנו מכפילים את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג מטבע. אמנם איננו יודעים את המספר בפועל, אך יש לנו ביטוי לייצג אותו.

וכך עכשיו להכפיל$\text{number}\cdot\text{value}=\text{total value}$. ראה כיצד הדבר נעשה בטבלה שלהלן.

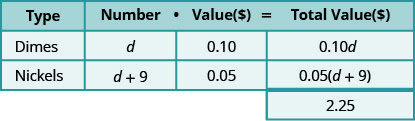
שימו לב שעשינו את כותרת הטבלה להציג את הדגם.

שלב 4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד. תרגם את המשפט האנגלי למשוואה אלגברית.

כתוב את המשוואה על ידי הוספת הערכים הכוללים של כל סוגי המטבעות.

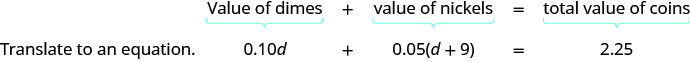
שלב 5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.

עכשיו לפתור את המשוואה הזו.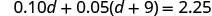
להפיץ.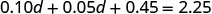
לשלב מונחים כמו.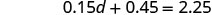
הפחת 0.45 מכל צד.
לחלק.
אז יש 12 אגורות.
מספר הניקלים הוא d+9d+9.
	21

שלב 6. בדוק את התשובה בבעיה וודא שהיא הגיונית.

האם זה בודק?

$$\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}$$

שלב 7. ענה על השאלה במשפט שלם.

לאדלברטו יש שתים עשרה אגורות ועשרים ואחד ניקל.

אם זה היה תרגיל שיעורי בית, העבודה שלנו עשויה להיראות כך.

נסה את זה $\PageIndex{1}$

למיכאלה יש 2.05 דולר בפרוטות וניקלים בארנק העודף שלה. יש לה שבעה אגורות יותר מניקלים. כמה מטבעות מכל סוג יש לה?

תשובה

9 ניקל, 16 אגורות

נסה את זה $\PageIndex{2}$

לליליאנה יש 2.10 דולר בניקלים ורבעים בתיק הגב שלה. יש לה 12 אגורות יותר מרבעים. כמה מטבעות מכל סוג יש לה?

תשובה

17 ניקל, 5 רבעים

לפתור בעיות של מילות מטבע.

1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
   • קבע את סוגי המטבעות המעורבים.
   • צור טבלה לארגון המידע.
   • תייג את העמודות "סוג", "מספר", "ערך", "ערך כולל".
   • רשום את סוגי המטבעות.
   • כתוב את הערך של כל סוג של מטבע.
   • כתוב את הערך הכולל של כל המטבעות.
   
2. זהה את מה שאנחנו מחפשים.
3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
   • השתמש בביטויים משתנים כדי לייצג את המספר של כל סוג מטבע ולכתוב אותם בטבלה.
   • הכפל את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג מטבע.
4. תרגם למשוואה.
   זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט למשוואה.
   כתוב את המשוואה על ידי הוספת הערכים הכוללים של כל סוגי המטבעות.
5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
7. ענה על השאלה במשפט שלם.

דוגמא $\PageIndex{2}$

למריה יש 2.43 דולר ברבעים ופרוטות בארנק. יש לה פי שניים יותר פרוטות מאשר רבעים. כמה מטבעות מכל סוג יש לה?

פתרון

שלב 1. קרא את הבעיה.

קבע את סוגי המטבעות המעורבים.

אנחנו יודעים שלמריה יש רבעים ופרוטות.

צור טבלה לארגון המידע.

• שלב 2. זהה את מה שאתה מחפש.
  • אנו מחפשים את מספר הרבעים והפרוטות.

  שלב 3. שם. ייצג את מספר הרבעונים והפרוטות באמצעות משתנים.

  • הכפל את 'המספר' ואת 'הערך' כדי לקבל את 'הערך הכולל' של כל סוג מטבע.

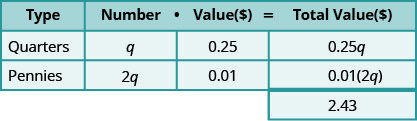
    שלב 4. תרגם. כתוב את המשוואה על ידי הוספת 'הערך הכולל' של כל סוגי המטבעות.

    $\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}$
    $\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}$
    $\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}$

נסה את זה $\PageIndex{3}$

לסומנטה יש 4.20 דולר בניקלים ומטבעות בבנק החזירון שלה. יש לה כפליים יותר מטבעות מאשר מטבעות. כמה מטבעות מכל סוג יש לה?

תשובה

42 ניקל, 21 אגורות

נסה את זה $\PageIndex{4}$

לאליסון יש פי שלושה מטבעות מאשר מטבעות בארנק. יש לה 9.35 דולר בסך הכל. כמה מטבעות מכל סוג יש לה?

תשובה

51 אגורות, 17 רבעים

בדוגמה הבאה נציג רק את הטבלה שהושלמה - זכור את הצעדים שאנו נוקטים כדי למלא את הטבלה.

דוגמא $\PageIndex{3}$

לדני יש פרוטות וניקלים בשווי 2.14 דולר בבנק החזרזיר שלו. מספר הניקלים הוא פי שניים יותר מעשר ממספר הפרוטות. כמה מטבעות וכמה פרוטות יש לדני?

פתרון

שלב 1. קרא את הבעיה.
קבע את סוגי המטבעות המעורבים.	פרוטות וניקלים
צור טבלה.
כתוב את הערך של כל סוג של מטבע.	פרוטות שוות 0.01 דולר. ניקל שווים 0.05 דולר.
שלב 2. זהה את מה שאנחנו מחפשים.	מספר הפרוטות והניקל
שלב 3. שם. ייצג את המספר של כל סוג מטבע באמצעות משתנים.
מספר הניקלים מוגדר במונחים של מספר הפרוטות, אז להתחיל עם פרוטות.	תן $p=$ מספר פרוטות.
מספר הניקלים הוא פי שניים יותר מעשר ממספר הפרוטות.	ותן $10p+2=$ מספר אגורות.
הכפל את המספר ואת הערך כדי לקבל את הערך הכולל של כל סוג של מטבע.
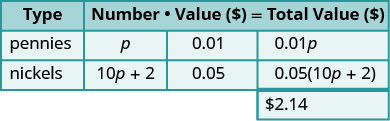שלב 4. תרגם. כתוב את המשוואה על ידי הוספת הערך הכולל של כל סוגי המטבעות.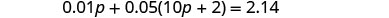
שלב 5. לפתור את המשוואה.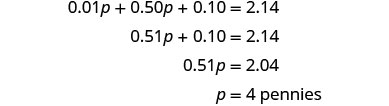
כמה אגורות?
שלב 6. בדוק את התשובה בבעיה וודא שזה הגיוני שלדני יש ארבע פרוטות ו 42 אגורות. האם הערך הכולל הוא 2.14$? $\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}$
שלב 7. תענה על השאלה.	לדני יש ארבע פרוטות ו-42 אגורות.

נסה את זה $\PageIndex{5}$

לג'סי יש מטבעות ומטבעות בשווי 6.55 דולר בכיס. מספר הניקלים הוא חמישה יותר מפי שניים ממספר הרבעונים. כמה מטבעות וכמה מטבעות יש לג'סי?

תשובה

41 ניקל, 18 רבעים

נסה את זה $\PageIndex{6}$

לאלן יש 7.00 דולר בסך הכל בפרוטות וניקלים בצנצנת המטבעות שלה. מספר הפרוטות שיש לאלן הוא שבע פחות משלוש פעמים ממספר הניקלים. כמה מכל מטבע יש לאלן?

תשובה

22 ניקל, 59 אגורות

לפתור בעיות כרטיסים וחותמות מילים

בעיות הכרוכות בכרטיסים או בולים דומות מאוד לבעיות מטבע. לכל סוג של כרטיס ובול יש ערך, בדיוק כמו כל סוג של מטבע. אז כדי לפתור בעיות אלה, נעקוב אחר אותם צעדים בהם השתמשנו כדי לפתור בעיות מטבע.

דוגמא $\PageIndex{4}$

בקונצרט בבית הספר, הערך הכולל של הכרטיסים שנמכרו היה 1,506 דולר. כרטיסים לסטודנטים נמכרו ב -6 דולר כל אחד וכרטיסים למבוגרים נמכרו ב -9 דולר כל אחד. מספר הכרטיסים למבוגרים שנמכרו היה פי חמישה פחות מפי שלושה ממספר כרטיסי הסטודנטים שנמכרו. כמה כרטיסי סטודנט וכמה כרטיסים למבוגרים נמכרו?

פתרון

שלב 1. קרא את הבעיה.

• קבע את סוגי הכרטיסים המעורבים. יש כרטיסים לסטודנטים וכרטיסים למבוגרים.
• צור טבלה לארגון המידע.

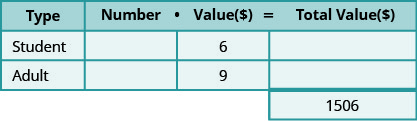
שלב 2. זהה את מה שאנחנו מחפשים.

• אנו מחפשים את מספר הכרטיסים לסטודנטים ולמבוגרים.

שלב 3. שם. ייצג את המספר של כל סוג כרטיס באמצעות משתנים.

אנו יודעים שמספר הכרטיסים למבוגרים שנמכרו היה פי חמישה פחות מפי שלושה ממספר כרטיסי הסטודנטים שנמכרו.

• הכפל את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג כרטיס.

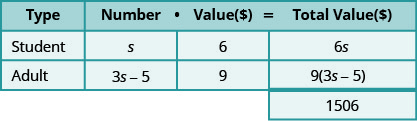
  שלב 4. תרגם. כתוב את המשוואה על ידי הוספת הערכים הכוללים של כל סוג כרטיס.

  $$6 s+9(3 s-5)=1506 \nonumber$$

  שלב 5. לפתור את המשוואה.

  $$\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber$$

  שלב 6. בדוק את התשובה.

  היו 47 כרטיסי סטודנטים ב -6 דולר כל אחד ו -136 כרטיסים למבוגרים ב -9 דולר כל אחד. האם הערך הכולל הוא 1,506$? אנו מוצאים את הערך הכולל של כל סוג כרטיס על ידי הכפלת מספר הכרטיסים כפול מערכו ואז להוסיף כדי לקבל את הערך הכולל של כל הכרטיסים שנמכרו.

  $$\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber$$

  שלב 7. תענה על השאלה. הם מכרו 47 כרטיסי סטודנט ו -136 כרטיסים למבוגרים.

נסה את זה $\PageIndex{7}$

ביום הראשון בטורניר פולו מים הערך הכולל של הכרטיסים שנמכרו היה 17,610 דולר. כרטיסים ליום אחד נמכרו ב -20 דולר ומעברי טורניר נמכרו ב -30 דולר. מספר כרטיסי הטורניר שנמכרו היה 37 יותר ממספר כרטיסי היום שנמכרו. כמה כרטיסי יום וכמה כרטיסי טורניר נמכרו?

תשובה

330 יום מעברים, 367 מעברי טורניר

נסה את זה $\PageIndex{8}$

באולם הקולנוע הערך הכולל של הכרטיסים שנמכרו היה 2,612.50 דולר. כרטיסים למבוגרים נמכרים ב -10 דולר כל אחד וכרטיסי בכיר/ילד נמכרים ב -7.50 דולר כל אחד. מספר הכרטיסים לקשיר/ילד שנמכרו היה 25 פחות מפי שניים ממספר הכרטיסים למבוגרים שנמכרו. כמה כרטיסי בכיר/ילד וכמה כרטיסים נמכרו?

תשובה

112 כרטיסים למבוגרים, 199 כרטיסים לבוקר/ילד

למדנו כיצד למצוא את המספר הכולל של הכרטיסים כאשר מספר כרטיס מסוג אחד מבוסס על מספר הסוג השני. לאחר מכן, נבחן דוגמה בה אנו יודעים את המספר הכולל של הכרטיסים ונצטרך להבין כיצד שני סוגי הכרטיסים קשורים זה לזה.

נניח שביאנקה מכרה בסך הכל 100 כרטיסים. כל כרטיס היה כרטיס מבוגר או כרטיס לילד. אם היא מכרה 20 כרטיסי ילדים, כמה כרטיסים למבוגרים היא מכרה?

• אמרת "80 "? איך הבנת את זה? חיסלת 20 מ-100?

אם היא מכרה 45 כרטיסי ילדים, כמה כרטיסים למבוגרים היא מכרה?

• אמרת "55 "? איך מצאת את זה? על ידי חיסור 45 מ 100?

מה אם היא מכרה 75 כרטיסי ילדים? כמה כרטיסים למבוגרים היא מכרה?

• מספר הכרטיסים למבוגרים חייב להיות 100—75. היא מכרה 25 כרטיסים למבוגרים.

עכשיו, נניח שביאנקה מכרה x כרטיסי ילד. אז כמה כרטיסים למבוגרים היא מכרה? כדי לגלות, היינו עוקבים אחר אותו היגיון בו השתמשנו לעיל. בכל מקרה, חיסרנו את מספר כרטיסי הילדים מ- 100 כדי לקבל את מספר הכרטיסים למבוגרים. עכשיו אנחנו עושים את אותו הדבר עם x.

סיכמנו זאת להלן.

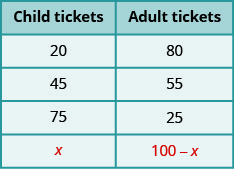
טבלה $\PageIndex{2}$

אנו יכולים ליישם טכניקות אלה על דוגמאות אחרות

דוגמא $\PageIndex{5}$

גאלן מכר 810 כרטיסים לקרנבל הכנסייה שלו בסכום כולל של 2,820 דולר. כרטיסי ילדים עולים 3 דולר כל אחד וכרטיסים למבוגרים עולים 5 דולר כל אחד. כמה כרטיסי ילדים וכמה כרטיסים למבוגרים הוא מכר?

פתרון

שלב 1. קרא את הבעיה.

• קבע את סוגי הכרטיסים המעורבים. יש כרטיסים לילדים וכרטיסים למבוגרים.
• צור טבלה לארגון המידע.

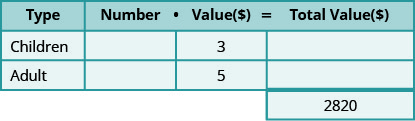
שלב 2. זהה את מה שאנחנו מחפשים.

• אנו מחפשים את מספר הכרטיסים לילדים ולמבוגרים.

שלב 3. שם. ייצג את המספר של כל סוג כרטיס באמצעות משתנים.

• המספר הכולל של הכרטיסים שנמכרו היה 810.
• המשמעות היא שמספר הכרטיסים לילדים בתוספת מספר הכרטיסים למבוגרים חייב להסתכם ב -810.
• בואו $c$ להיות מספר הכרטיסים לילדים.

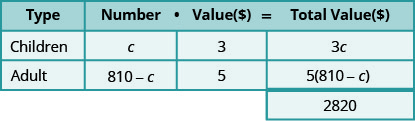
• ואז $810−c$ מספר הכרטיסים למבוגרים.
• הכפל את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג כרטיס.

שלב 4. תרגם.

כתוב את המשוואה על ידי הוספת הערכים הכוללים של כל סוג כרטיס.

שלב 5. לפתור את המשוואה.

$$\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}$$

כמה מבוגרים?

$$\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber$$

שלב 6. בדוק את התשובה. היו 615 כרטיסי ילדים ב -3 דולר כל אחד ו -195 כרטיסים למבוגרים ב -5 דולר כל אחד. האם הערך הכולל הוא 2,820 דולר?

$$\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber$$

שלב 7. תענה על השאלה. גאלן מכר 615 כרטיסי ילדים ו -195 כרטיסים למבוגרים.

נסה את זה $\PageIndex{9}$

במהלך המשמרת שלה בדוכן הכרטיסים למוזיאון מכרה לאה 115 כרטיסים בסך כולל של 1,163 דולר. כרטיסים למבוגרים עולים 12 דולר וכרטיסי סטודנטים עולים 5 דולר. כמה כרטיסים למבוגרים וכמה כרטיסי סטודנט מכרה לאה?

תשובה

84 כרטיסים למבוגרים, 31 כרטיסי סטודנט

נסה את זה $\PageIndex{10}$

על סיפון ספינת צפייה בלווייתנים היו 40 נוסעים משלמים. הסכום שנאסף מכרטיסים היה 1,196 דולר. נוסעים במחיר מלא שילמו 32 דולר כל אחד ונוסעים במחיר מוזל שילמו 26 דולר כל אחד. כמה נוסעים במחיר מלא וכמה נוסעים במחיר מוזל היו על הספינה?

תשובה

26 תעריף מלא, 14 תעריפים מוזלים

עכשיו, נעשה אחד שבו נמלא את השולחן בבת אחת.

דוגמא $\PageIndex{6}$

מוניקה שילמה 8.36 דולר עבור בולים. מספר הבולים של 41 סנט היה ארבעה יותר מפי שניים ממספר הבולים של שני סנט. כמה בולים של 41 סנט וכמה בולים של שני סנט מוניקה קנתה?

פתרון

סוגי הבולים הם בולים של 41 סנט וחותמות של שני סנט. שמותיהם גם נותנים את הערך!

"מספר הבולים של 41 סנט היה ארבעה יותר מפי שניים ממספר הבולים של שני סנט."

$$\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber$$

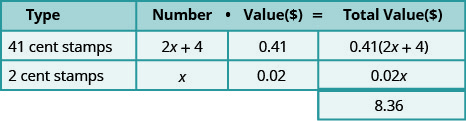
$$\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber$$

בדוק.

$$\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}$$
$$\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber$$

נסה את זה $\PageIndex{11}$

אריק שילם 13.36 דולר עבור בולים. מספר הבולים של 41 סנט היה שמונה יותר מפי שניים ממספר הבולים של שני סנט. כמה בולים של 41 סנט וכמה בולים של שני סנט אריק קנה?

תשובה

32 במחיר של 0.41 דולר, 12 במחיר של 0.02 דולר

נסה את זה $\PageIndex{12}$

קיילי שילם 12.66 דולר עבור בולים. מספר הבולים של 41 סנט היה פי ארבעה פחות משלושה ממספר הבולים של 20 סנט. כמה בולים של 41 סנט וכמה בולים של 20 סנט קנתה קיילי?

תשובה

26 במחיר של 0.41 דולר, 10 במחיר של 0.20 דולר

לפתור בעיות מילים של תערובת

עכשיו נפתור כמה יישומים כלליים יותר של מודל התערובת. מכולת וברמנים משתמשים במודל התערובת כדי לקבוע מחיר הוגן למוצר העשוי מערבוב של שני מרכיבים או יותר. מתכננים פיננסיים משתמשים במודל התערובת כאשר הם משקיעים כסף במגוון חשבונות ורוצים למצוא את הריבית הכוללת. מעצבי נוף משתמשים במודל התערובת כאשר יש להם מבחר צמחים ותקציב קבוע, ורכזי אירועים עושים את אותו הדבר בבחירת מתאבנים ומנות ראשונות למשתה.

בעיית מילת התערובת הראשונה שלנו תהיה הכנת תערובת שבילים מצימוקים ואגוזים.

דוגמא $\PageIndex{7}$

הנינג מערבב צימוקים ואגוזים כדי להכין 10 פאונד של תערובת שבילים. צימוקים עולים 2 דולר לקילו ואגוזים עולים 6 דולר לקילו. אם הנינג רוצה שהעלות שלו לתערובת השבילים תהיה 5.20 דולר לקילו, כמה קילוגרמים של צימוקים וכמה קילוגרמים של אגוזים עליו להשתמש?

פתרון

כמו בעבר, אנו ממלאים תרשים לארגון המידע שלנו.

10 הקילוגרמים של תערובת השבילים יגיעו מערבוב צימוקים ואגוזים.

$$\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber$$

אנו מזינים את המחיר לפאונד עבור כל פריט.

אנו מכפילים את המספר כפול הערך כדי לקבל את הערך הכולל.

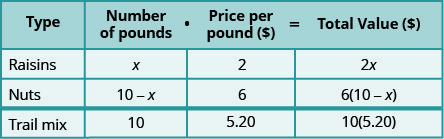
שים לב כי השורה האחרונה בטבלה נותן את המידע עבור הסכום הכולל של התערובת.

אנו יודעים שערך הצימוקים בתוספת ערך האגוזים יהיה הערך של תערובת השבילים.

כתוב את המשוואה מתוך הערכים הכוללים.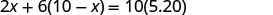
לפתור את המשוואה.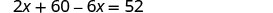
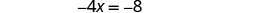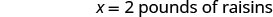מצא את מספר קילוגרמים של אגוזים.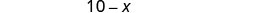
	8 קילו אגוזים
בדוק. $\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}$
	הנינג ערבב שני קילו צימוקים עם שמונה קילו אגוזים.

נסה את זה $\PageIndex{13}$

אורלנדו מערבבת אגוזים וריבועי דגנים כדי להכין תערובת מסיבות. אגוזים נמכרים ב -7 דולר לקילו וריבועי דגנים נמכרים ב -4 דולר לקילו. אורלנדו רוצה להכין 30 פאונד של תערובת מסיבות בעלות של 6.50 דולר לקילו, כמה קילוגרמים של אגוזים וכמה קילוגרמים של ריבועי דגנים עליו להשתמש?

תשובה

5 קילו ריבועי דגנים, 25 קילו אגוזים

נסה את זה $\PageIndex{14}$

בקה רוצה לערבב מיץ פירות וסודה כדי להכין אגרוף. היא יכולה לקנות מיץ פירות ב -3 דולר לליטר וסודה ב -4 דולר לליטר. אם היא רוצה להכין 28 ליטר אגרוף בעלות של 3.25 דולר לליטר, כמה ליטרים של מיץ פירות וכמה ליטרים של סודה עליה לקנות?

תשובה

21 ליטרים של אגרוף פירות, 7 ליטר סודה

אנו יכולים גם להשתמש במודל התערובת כדי לפתור בעיות השקעה באמצעות ריבית פשוטה. השתמשנו בנוסחת הריבית הפשוטה,$I=Prt$, שבו $t$ ייצג את מספר השנים. כאשר אנחנו רק צריכים למצוא את הריבית לשנה אחת$t=1$, אז אז$I=Pr$.

דוגמא $\PageIndex{8}$

לסטייסי יש 20 אלף דולר להשקיע בשני חשבונות בנק שונים. חשבון אחד משלם ריבית בשיעור של 3% לשנה והחשבון השני משלם ריבית בשיעור של 5% לשנה. כמה היא צריכה להשקיע בכל חשבון אם היא רוצה להרוויח 4.5% ריבית בשנה על הסכום הכולל?

פתרון

אנו נמלא תרשים לארגון המידע שלנו. אנו נשתמש בנוסחת הריבית הפשוטה כדי למצוא את הריבית שנצברה בחשבונות השונים.

הריבית על ההשקעה המעורבת תגיע מהוספת הריבית מהחשבון המרוויח 3% והריבית מהחשבון המרוויח 5% כדי לקבל את הריבית הכוללת על 20,000$.

$$\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}$$

הסכום שהושקע הוא הקרן עבור כל חשבון.

אנו מזינים את הריבית עבור כל חשבון.

אנו מכפילים את הסכום שהושקע כפול התעריף כדי לקבל את הריבית.

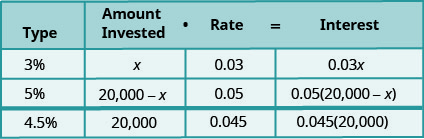
שימו לב כי הסכום הכולל שהושקע, 20,000, הוא סכום הסכום שהושקע ב -3% והסכום שהושקע ב -5%. והריבית הכוללת$0.045(20,000)$,, היא סכום הריבית שנצברה בחשבון 3% והריבית שנצברה בחשבון 5%.

בדומה ליישומי התערובת האחרים, העמודה האחרונה בטבלה נותנת לנו את המשוואה לפתור.

כתוב את המשוואה מהריבית שנצברה. לפתור את המשוואה.	$\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}$
מצא את הסכום שהושקע ב -5%.
בדוק. $\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}$
	סטייסי צריכה להשקיע 5,000 דולר בחשבון שמרוויח 3% ו -15,000 דולר בחשבון שמרוויח 5%.

נסה את זה $\PageIndex{15}$

לרמי יש 14,000 דולר להשקיע בשתי קרנות נאמנות. קרן אחת משלמת ריבית בשיעור של 4% לשנה והקרן השנייה משלמת ריבית בשיעור של 7% לשנה. כמה היא צריכה להשקיע בכל קרן אם היא רוצה להרוויח 6.1% ריבית על הסכום הכולל?

תשובה

4,200 דולר ב -4%, 9,800 דולר ב -7%

נסה את זה $\PageIndex{16}$

למרקו יש 8,000 דולר לחסוך ללימודי הקולג' של בתו. הוא רוצה לחלק אותו בין חשבון אחד שמשלם ריבית של 3.2% לשנה לחשבון אחר שמשלם ריבית של 8% בשנה. כמה עליו להשקיע בכל חשבון אם הוא רוצה שהריבית על סך ההשקעה תהיה 6.5%?

תשובה

2,500 דולר ב -3.2%, 5,500 דולר ב -8%

מושגי מפתח

• ערך כולל של מטבעות עבור אותו סוג מטבע, הערך הכולל של מספר מטבעות נמצא באמצעות המודל.
  number·value = ערך כולל כאשר המספר הוא מספר המטבעות והערך הוא הערך של כל מטבע; הערך הכולל הוא הערך הכולל של כל המטבעות
• אסטרטגיה לפתרון בעיות - בעיות מילות מטבע
  1. קרא את הבעיה. הפוך את כל המילים והרעיונות להבנה. קבע את סוגי המטבעות המעורבים.
     • צור טבלה לארגון המידע.
     • סמן את סוג העמודות, מספר, ערך, ערך כולל.
     • רשום את סוגי המטבעות.
     • כתוב את הערך של כל סוג של מטבע.
     • כתוב את הערך הכולל של כל המטבעות.
  2. זהה את מה שאנחנו מחפשים.
  3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
     השתמש בביטויים משתנים כדי לייצג את המספר של כל סוג מטבע ולכתוב אותם בטבלה.
     הכפל את המספר כפול הערך כדי לקבל את הערך הכולל של כל סוג מטבע.
  4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט למשוואה.
     כתוב את המשוואה על ידי הוספת הערכים הכוללים של כל סוגי המטבעות.
  5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
  6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
  7. ענה על השאלה במשפט שלם.

רשימת מילים

בעיות תערובת

בעיות תערובת משלבות שני פריטים או יותר עם ערכים שונים יחד.