1.6: דמיינו שברים
- Page ID
- 205650
בסוף פרק זה, תוכל:
- מצא שברים שווים
- פשט שברים
- הכפל שברים
- מחלקים שברים
- פשט ביטויים שנכתבו באמצעות סרגל שבר
- תרגם ביטויים לביטויים עם שברים
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, שברים.
מצא שברים שווים
שברים הם דרך לייצג חלקים של שלם. השבר \(\dfrac{1}{3}\) פירושו ששלם אחד חולק לשלושה חלקים שווים וכל חלק הוא אחד משלושת החלקים השווים. ראה איור\(\PageIndex{1}\). השבר \(\dfrac{2}{3}\) מייצג שניים משלושה חלקים שווים. בשבר\(\dfrac{2}{3}\), ה- 2 נקרא המונה וה -3 נקרא המכנה.
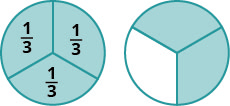
ביצוע פעילות המתמטיקה המניפולטיבית "שברי מודל" יעזור לכם לפתח הבנה טובה יותר של שברים, המונים והמכנים שלהם.
חלק כתוב\(\dfrac{a}{b}\), איפה \(b\neq 0\) ו
- \(a\)הוא המונה \(b\) והוא המכנה.
חלק מייצג חלקים של שלם. המכנה \(b\) הוא מספר החלקים השווים אליהם חולק השלם, והממונה \(a\) מציין כמה חלקים כלולים.
אם פשטידה שלמה נחתכה ל -6 חלקים ואנחנו אוכלים את כל 6 החלקים, אכלנו \(\dfrac{6}{6}\) חתיכות, או במילים אחרות, פשטידה אחת שלמה.
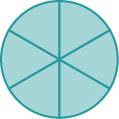
אז\(\dfrac{6}{6}=1\). זה מוביל אותנו לתכונה של אחד שאומר לנו שכל מספר, למעט אפס, המחולק מעצמו הוא\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
כל מספר, למעט אפס, מחולק בפני עצמו הוא אחד.
ביצוע פעילות המתמטיקה המניפולטיבית "שברים שווים לאחד" יעזור לך לפתח הבנה טובה יותר של שברים השווים לאחד.
אם פשטידה נחתכה ב -6 חלקים ואכלנו את כל 6, אכלנו \(\dfrac{6}{6}\) חתיכות, או במילים אחרות, פשטידה אחת שלמה. אם הפשטידה נחתכה ל -8 חתיכות ואכלנו את כל 8, אכלנו \(\dfrac{8}{8}\) חתיכות, או פשטידה אחת שלמה. אכלנו אותה כמות - עוגה אחת שלמה.
השברים \(\dfrac{6}{6}\) ויש \(\dfrac{8}{8}\) להם אותו ערך, 1, ולכן הם נקראים שברים שווים. שברים שווים הם שברים בעלי ערך זהה.
בואו נחשוב על פיצות הפעם. איור \(\PageIndex{3}\) מציג שתי תמונות: פיצה אחת בצד שמאל, לחתוך לשתי חתיכות שוות, ופיצה שנייה באותו גודל, לחתוך לשמונה חתיכות בצד ימין. זו דרך להראות שזה \(\dfrac{1}{2}\) שווה ערך ל\(\dfrac{4}{8}\). במילים אחרות, הם שברים שווים.
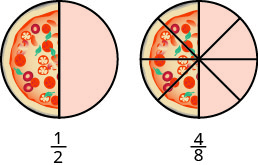
שברים שווים הם שברים בעלי ערך זהה.
איך אנחנו יכולים להשתמש במתמטיקה כדי לשנות \(\dfrac{1}{2}\)\(\dfrac{4}{8}\)? איך נוכל לקחת פיצה שנחתכת ל -2 חלקים ולחתוך אותה ל -8 חלקים? נוכל לחתוך כל אחד משני החלקים הגדולים ל -4 חלקים קטנים יותר! לאחר מכן כל הפיצה תיחתך ל -88 חתיכות במקום 2 בלבד. מבחינה מתמטית, מה שתיארנו יכול להיכתב כך. \(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\) ראה איור\(\PageIndex{4}\).
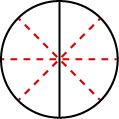
מודל זה מוביל לנכס הבא:
אם \(a,b,c\) יש מספרים איפה\(b\neq 0, c\neq 0\), אז
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
אם היינו חותכים את הפיצה אחרת, היינו יכולים לקבל
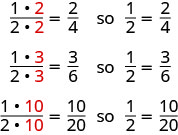
אז, אנחנו אומרים\(\dfrac{1}{2}\), \(\dfrac{2}{4}\)\(\dfrac{3}{6}\),, \(\dfrac{10}{20}\) והם שברים שווים.
ביצוע פעילות המתמטיקה המניפולטיבית "שברים שווים" יעזור לך לפתח הבנה טובה יותר של המשמעות כאשר שני שברים שווים.
מצא שלושה שברים שווים ל\(\dfrac{2}{5}\).
- תשובה
-
כדי למצוא שבר שווה ערך ל\(\dfrac{2}{5}\), אנו מכפילים את המונה והמכנה באותו מספר. אנו יכולים לבחור כל מספר, למעט אפס. בואו נכפיל אותם ב -2, 3 ואז 5.
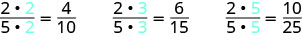
-
אז,\(\dfrac{4}{10}\),\(\dfrac{6}{15}\), \(\dfrac{10}{25}\) והם שווים ל\(\dfrac{2}{5}\).
מצא שלושה שברים שווים ל\(\dfrac{3}{5}\).
- תשובה
-
\(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\); התשובות עשויות להשתנות
מצא שלושה שברים שווים ל\(\dfrac{4}{5}\).
- תשובה
-
\(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\); התשובות עשויות להשתנות
פשט שברים
שבר נחשב לפשוט יותר אם אין גורמים משותפים, מלבד 1, במונה ובמכנה שלו.
לדוגמה,
- \(\dfrac{2}{3}\)הוא פשוט כי אין גורמים נפוצים של 2 ו 3.
- \(\dfrac{10}{15}\)אינו פשוט כי 5 הוא גורם משותף של 10 ו -15.
שבר נחשב לפשוט יותר אם אין גורמים משותפים במונה ובמכנה שלו.
הביטוי להפחית שבריר פירושו לפשט את השבר. אנו מפשטים, או מצמצמים, שבר על ידי הסרת הגורמים המשותפים של המונה והמכנה. חלק אינו מפושט עד להסרת כל הגורמים הנפוצים. אם לביטוי יש שברים, הוא לא מפושט לחלוטין עד לפישוט השברים.
בתרגיל \(\PageIndex{4}\) השתמשנו במאפיין השברים המקבילים כדי למצוא שברים שווים. כעת נשתמש במאפיין השברים המקביל הפוך כדי לפשט שברים. אנחנו יכולים לשכתב את הנכס כדי להציג את שתי הצורות יחד.
אם \(a,b,c\) יש מספרים איפה\(b\neq 0,c\neq 0\),
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
פשט: \(-\dfrac{32}{56}\)
- תשובה
-
\(-\dfrac{32}{56}\) כתוב מחדש את המונה והמכנה המציג את הגורמים המשותפים. \(-\dfrac{4\cdot 8}{7\cdot 8}\) פשט את השימוש במאפיין השברים המקבילים. \(-\dfrac{4}{7}\) שימו לב שהשבר \(-\dfrac{4}{7}\) מפושט מכיוון שאין גורמים נפוצים יותר.
פשט: \(-\dfrac{42}{54}\)
- תשובה
-
\(-\dfrac{7}{9}\)
פשט: \(-\dfrac{30}{54}\)
- תשובה
-
\(-\dfrac{5}{9}\)
לפעמים זה לא יכול להיות קל למצוא גורמים משותפים של המונה והמכנה. כאשר זה קורה, רעיון טוב הוא להביא בחשבון את המונה והמכנה למספר ראשוני s ואז לחלק את הגורמים המשותפים באמצעות מאפיין השברים המקבילים.
פשט: \(-\dfrac{210}{385}\)
- תשובה
-



פשט: \(-\dfrac{69}{120}\)
- תשובה
-
\(-\dfrac{23}{40}\)
פשט: \(-\dfrac{120}{192}\)
- תשובה
-
\(-\dfrac{5}{8}\)
כעת אנו מסכמים את הצעדים שעליכם לבצע כדי לפשט שברים.
- כתוב מחדש את המונה והמכנה כדי להראות את הגורמים המשותפים.
במידת הצורך, הכניסו תחילה את המונה והמכנה למספרים ראשוניים. - פשט את השימוש במאפיין השברים המקבילים על ידי חלוקת גורמים משותפים.
- הכפל את כל הגורמים שנותרו, במידת הצורך.
פשט: \(\dfrac{5x}{5y}\)
- תשובה
-
\(\dfrac{5x}{5y}\) כתוב מחדש את הצגת הגורמים הנפוצים, ואז חלק את הגורמים הנפוצים. 
לפשט. \(\dfrac{x}{y}\)
פשט: \(\dfrac{7x}{7y}\)
- תשובה
-
\(\dfrac{x}{y}\)
פשט: \(\dfrac{3a}{3b}\)
- תשובה
-
\(\dfrac{a}{b}\)
הכפל שברים
אנשים רבים מוצאים הכפלה וחלוקת שברים קלים יותר מאשר הוספה וחיסור של שברים. אז נתחיל בכפל שברים.
ביצוע הפעילות המתמטית המניפולטיבית "כפל שברי מודל" יעזור לך לפתח הבנה טובה יותר של הכפלת שברים.
נשתמש במודל כדי להראות לך כיצד להכפיל שני שברים ולעזור לך לזכור את ההליך. בואו נתחיל עם\(\dfrac{3}{4}\).

עכשיו אנחנו ניקח \(\dfrac{1}{2}\)\(\dfrac{3}{4}\).

שימו לב שעכשיו, השלם מחולק ל 8 חלקים שווים. אז\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
כדי להכפיל שברים, אנו מכפילים את המספרים ומכפילים את המכנים.
אם \(a,b,c\) \(d\) והם מספרים איפה \(b\neq 0\) ו\(d\neq 0\), אז
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
כדי להכפיל שברים, הכפל את המספרים והכפיל את המכנים.
כאשר מכפילים שברים, המאפיינים של מספרים חיוביים ושליליים עדיין חלים, כמובן. זה רעיון טוב כדי לקבוע את הסימן של המוצר כצעד הראשון. בתרגיל \(\PageIndex{13}\) נכפיל שלילי וחיובי, כך שהמוצר יהיה שלילי.
הכפל: \(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- תשובה
-
הצעד הראשון הוא למצוא את הסימן של המוצר. מכיוון שהסימנים הם שונים, המוצר שלילי.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
הכפל: \(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- תשובה
-
\(-\dfrac{4}{21}\)
הכפל: \(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- תשובה
-
\(-\dfrac{3}{16}\)
כאשר מכפילים שבר במספר שלם, זה עשוי להיות מועיל לכתוב את המספר השלם כשבר. כל מספר שלם, א, ניתן לכתוב כ\(\dfrac{a}{1}\). כך, למשל,\(3 = \dfrac{3}{1}\).
הכפל: \(-\dfrac{12}{5}(-20x)\)
- תשובה
-
קבע את סימן המוצר. הסימנים זהים, ולכן המוצר חיובי.
\(-\dfrac{12}{5}(-20x)\) כתוב \(20x\) כשבריר. \(\dfrac{12}{5}(\dfrac{20x}{1})\) להכפיל. כתוב מחדש \(20\) כדי להראות את הגורם המשותף \(5\) ולחלק אותו. 
לפשט. \(48x\)
הכפל: \(\dfrac{11}{3}(-9a)\)
- תשובה
-
\(-33a\)
הכפל: \(\dfrac{13}{7}(-14b)\)
- תשובה
-
\(-26b\)
מחלקים שברים
עכשיו כשאנחנו יודעים להכפיל שברים, אנחנו כמעט מוכנים לחלק. לפני שנוכל לעשות זאת, אנו זקוקים לאוצר מילים כלשהו.
ההדדיות של שבר נמצאת על ידי היפוך השבר, הצבת המונה במכנה והמכנה במונה. ההדדי של \(\dfrac{2}{3}\) הוא\(\dfrac{3}{2}\).
שים לב לזה\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). מספר וההדדיות שלו מתרבים ל\(1\).
כדי לקבל תוצר חיובי \(1\) בעת הכפלת שני מספרים, המספרים חייבים להיות בעלי אותו סימן. אז הדדיות חייבות להיות בעלות אותו סימן.
ההדדי של \(-\dfrac{10}{7}\) הוא\(-\dfrac{7}{10}\), מאז\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
ההדדי של \(\dfrac{a}{b}\) הוא\(\dfrac{b}{a}\).
מספר וההדדיות שלו מתרבים לאחד \(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
ביצוע הפעילות המתמטית המניפולטיבית "חטיבת שברי מודלים" יעזור לך לפתח הבנה טובה יותר של חלוקת שברים.
כדי לחלק שברים, אנו מכפילים את השבר הראשון בהדדיות של השני.
אם \(a,b,c\) \(d\) והם מספרים איפה \(b\neq 0, c\neq 0\) ו\(d\neq 0\), אז
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
כדי לחלק שברים, אנו מכפילים את השבר הראשון בהדדיות של השני.
אנחנו צריכים \(d\neq 0\) לומר \(b\neq 0, c\neq 0\) ולהיות בטוחים שאנחנו לא מתחלקים באפס!
לחלק: \(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- תשובה
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
לחלק:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- תשובה
-
\(-\dfrac{21}{5p}\)
לחלק:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- תשובה
-
\(-\dfrac{15}{8q}\)
מצא את המנה:
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- תשובה
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) כדי לחלק, הכפל את השבר הראשון בהדדיות של השני. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) לקבוע את הסימן של המוצר, ולאחר מכן להכפיל.. \(\dfrac{7\cdot 27}{18\cdot 14}\) שכתוב מחדש מראה גורמים נפוצים. 
הסר גורמים נפוצים. \(\dfrac{3}{2\cdot 2}\) לפשט. \(\dfrac{3}{4}\)
מצא את המנה:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- תשובה
-
\(\dfrac{4}{15}\)
מצא את המנה:
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- תשובה
-
\(\dfrac{2}{3}\)
ישנן מספר דרכים לזכור אילו צעדים לנקוט כדי להכפיל או לחלק שברים. דרך אחת היא לחזור על הקריאה לעצמך. אם תעשה זאת בכל פעם שאתה מבצע תרגיל, תשנן את הצעדים.
- "כדי להכפיל שברים, הכפל את המספרים והכפיל את המכנים."
- "כדי לחלק שברים, הכפל את השבר הראשון בהדדיות של השני."
דרך נוספת היא לזכור שתי דוגמאות:
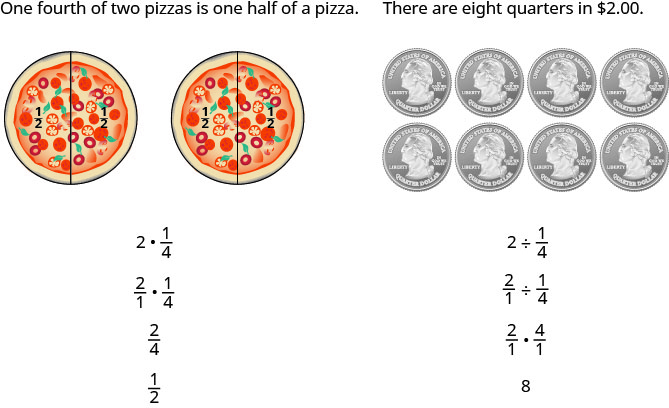
המספרים או המכנים של שברים מסוימים מכילים שברים עצמם. שבר בו המונה או המכנה הוא שבר נקרא שבר מורכב.
שבר מורכב הוא שבר בו המונה או המכנה מכילים שבר.
כמה דוגמאות לשברים מורכבים הם:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
כדי לפשט שבר מורכב, אנו זוכרים כי סרגל השבר פירושו חלוקה. לדוגמה, השבר המורכב \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) פירושו\(\dfrac{3}{4} \div \dfrac{5}{8}\).
פשט: \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- תשובה
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) לשכתב כחלוקה. \(\dfrac{3}{4} \div \dfrac{5}{8}\) הכפל את השבר הראשון בהדדיות של השני. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) להכפיל. \(\dfrac{3\cdot 8}{4\cdot 5}\) חפש גורמים נפוצים. 
חלקו גורמים נפוצים ופשטו. \(\dfrac{6}{5}\)
פשט: \(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- תשובה
-
\(\dfrac{4}{5}\)
פשט: \(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- תשובה
-
\(\dfrac{11}{14}\)
פשט: \(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- תשובה
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) לשכתב כחלוקה. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) הכפל את השבר הראשון בהדדיות של השני. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) להכפיל. \(\dfrac{x\cdot 6}{2\cdot xy}\) חפש גורמים נפוצים. 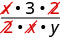
חלקו גורמים נפוצים ופשטו. \(\dfrac{3}{y}\)
פשט: \(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- תשובה
-
\(\dfrac{3}{4b}\)
פשט: \(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- תשובה
-
\(\dfrac{4}{q}\)
פשט ביטויים עם סרגל שבר
הקו המפריד בין המונה למכנה בשבר נקרא סרגל שבר. סרגל שבר משמש כסמל קיבוץ. סדר הפעולות אומר לנו לפשט את המונה ואז את המכנה. ואז אנחנו מתחלקים.
כדי לפשט את הביטוי\(\dfrac{5 - 3}{7 + 1}\), ראשית אנו מפשטים את המונה ואת המכנה בנפרד. ואז אנחנו מתחלקים.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- פשט את הביטוי במונה. פשט את הביטוי במכנה.
- פשט את השבר.
פשט: \(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- תשובה
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
פשט: \(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- תשובה
-
\(-\dfrac{3}{4}\)
פשט: \(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- תשובה
-
\(-\dfrac{5}{3}\)
לאן הסימן השלילי הולך בשבריר? בדרך כלל הסימן השלילי נמצא מול השבר, אך לעיתים תראו שבר עם מונה שלילי, או לפעמים עם מכנה שלילי. זכור כי שברים מייצגים חלוקה. כאשר למונה ולמכנה יש סימנים שונים, המנה שלילית.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
עבור כל מספרים \(a\) חיוביים\(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
פשט: \(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- תשובה
-
סרגל השבר פועל כמו סמל קיבוץ. אז לפשט לחלוטין את המונה ואת המכנה בנפרד.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
פשט: \(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- תשובה
-
\(4\)
פשט: \(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- תשובה
-
\(2\)
תרגם ביטויים לביטויים עם שברים
כעת, לאחר שביצענו עבודה עם שברים, אנו מוכנים לתרגם ביטויים שיגרמו לביטויים עם שברים.
המילים באנגלית quotient ויחס משמשות לעתים קרובות לתיאור שברים. זכור כי "מנה" פירושו חלוקה. המנה של aa ו- bb היא התוצאה שאנו מקבלים מחלוקת \(a\) על ידי\(b\), או. \(\dfrac{a}{b}\)
תרגם את הביטוי האנגלי לביטוי אלגברי: כמות ההבדל של \( m\) ו, ו. \(n\) \(p\)
- תשובה
-
אנחנו מחפשים את המנה של ההבדל של \(m\) ו\(n\), ו.. \(p\) זה אומר שאנחנו רוצים לחלק את ההבדל של \(m\) ו\(n\), ו\(p\).
\[\dfrac{m - n}{p}\]
תרגם את הביטוי האנגלי לביטוי אלגברי: כמות ההבדל של \(a\) ו, ו. \(b\) \(cd\)
- תשובה
-
\(\dfrac{a - b}{cd}\)
תרגם את הביטוי האנגלי לביטוי אלגברי: המנה של \(p\) סכום ו, ו. \(q\) \(r\)
- תשובה
-
\(\dfrac{p + q}{r}\)
מושגי מפתח
- מאפיין שברים שווה ערך: אם \(a, b, c\) הם מספרים היכן\(b\neq 0, c\neq 0\), ואז
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) ו \(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - חלוקת שברים: אם \(a, b, c\) \(d\) והם מספרים איפה \(b\neq 0, c\neq 0\) ואז\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). \(d \neq 0\) כדי לחלק שברים, הכפל את השבר הראשון בהדדיות של השני.
- כפל שברים: אם \(a,b,c\) ומספרים \(d\) היכן\(b\neq 0, d\neq 0\), אז\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). כדי להכפיל שברים, הכפל את המספרים והכפיל את המכנים.
- מיקום סימן שלילי בשבר: לכל מספרים חיוביים \(a\) ו\(b\), \(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- רכוש של אחד:\(\dfrac{a}{a} = 1\); כל מספר, למעט אפס, מחולק בפני עצמו הוא אחד.
- פשט שבר
- כתוב מחדש את המונה והמכנה כדי להראות את הגורמים המשותפים. במידת הצורך, הכניסו תחילה את המונה והמכנה למספרים ראשוניים.
- פשט את השימוש במאפיין השברים המקבילים על ידי חלוקת גורמים משותפים.
- הכפל את כל הגורמים שנותרו.
- פשט ביטוי באמצעות סרגל שבר
- פשט את הביטוי במונה. פשט את הביטוי במכנה.
- פשט את השבר.
רשימת מילים
- שבר מורכב
- שבר מורכב הוא שבר בו המונה או המכנה מכילים שבר.
- מכנה
- המכנה הוא הערך בחלק התחתון של השבר המציין את מספר החלקים השווים אליהם חולק השלם.
- שברים שווים
- שברים שווים הם שברים בעלי ערך זהה.
- שבריר
- כתוב שבר\(\frac{a}{b}\), כאשר\(b\neq 0\), a הוא המונה ו- b הוא המכנה. חלק מייצג חלקים של שלם. המכנה b הוא מספר החלקים השווים אליהם חולק השלם, והמונה aa מציין כמה חלקים כלולים.
- מונה
- המונה הוא הערך בחלקו העליון של השבר המציין כמה חלקים מהשלם כלולים.
- הדדי
- ההדדי של \(\frac{a}{b}\) הוא\(\frac{b}{a}\). מספר וההדדיות שלו מתרבים לאחד:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- שבר פשוט
- שבר נחשב לפשוט יותר אם אין גורמים משותפים במונה ובמכנה שלו.


