10.E: Analytic Jiometri (Mazoezi)

10.1: duaradufu

Katika sehemu hii, sisi kuchunguza sura ya chumba hiki na maombi yake halisi ya dunia, ikiwa ni pamoja na jinsi mbali mbali watu wawili katika Statuary Hall wanaweza kusimama na bado kusikia kila mmoja whisper.

Maneno

1) Eleza ellipse kwa suala la foci yake.

Jibu

Ellipse ni seti ya pointi zote katika ndege, jumla ya umbali wake kutoka pointi mbili fasta, inayoitwa foci, ni mara kwa mara.

2) Ambapo lazima foci ya ellipse uongo?

3) Ni kesi gani maalum ya ellipse tunayo wakati mhimili mkubwa na mdogo una urefu sawa?

Jibu

Kesi hii maalum itakuwa mduara.

4) Kwa kesi maalum iliyotajwa hapo juu, itakuwa nini kweli kuhusu foci ya ellipse hiyo?

5) Ni nini kinachoweza kusema juu ya ulinganifu wa grafu ya ellipse na kituo cha asili na foci kando ya$y$ -axis?

Jibu

Ni sawa kuhusu$x$ -axis,$y$ -axis, na asili.

Kialjebra

Kwa mazoezi 6-10, onyesha kama equations iliyotolewa inawakilisha ellipses. Ikiwa ndiyo, andika kwa fomu ya kawaida.

6)$2x^2 +y=4$

7)$4x^2 + 9y^2=36$

Jibu

ndiyo;$\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1$

8)$4x^2 - y^2=4$

9)$4x^2 + 9y^2=1$

Jibu

ndiyo;$\dfrac{x^2}{\left (\tfrac{1}{2} \right )^2}+\dfrac{y^2}{\left (\tfrac{1}{2} \right )^2}=1$

10)$4x^2-8x+9y^2-72y+112=0$

Kwa mazoezi 11-26, andika equation ya duaradufu katika fomu ya kawaida, na kutambua pointi za mwisho za shoka kuu na ndogo pamoja na foci.

11)$\dfrac{x^2}{4}+\dfrac{y^2}{49}=1$

Jibu

$\dfrac{x^2}{2^2}+\dfrac{y^2}{7^2}=1$; Endpoints ya mhimili kuu$(0,7)$ na$(0,-7)$. Mwisho wa mhimili mdogo$(2,0)$ na$(-2,0)$. Foci katika$(0, 3\sqrt{5})$,$(0, -3\sqrt{5})$.

12)$\dfrac{x^2}{100}+\dfrac{y^2}{64}=1$

13)$x^2 + 9y^2 = 1$

Jibu

$\dfrac{x^2}{(1)^2}+\dfrac{y^2}{\left (\tfrac{1}{3} \right )^2}=1$; Endpoints ya mhimili kuu$(1,0)$ na$(-1,0)$. Mwisho wa mhimili mdogo$\left (0, \dfrac{1}{3} \right )$,$\left (0, -\dfrac{1}{3} \right )$. Foci katika$\left (\dfrac{2\sqrt{2}}{3}, 0 \right )$,$\left (-\dfrac{2\sqrt{2}}{3}, 0 \right )$.

14)$4x^2 + 16y^2 = 1$

15)$\dfrac{(x-2)^2}{49}+\dfrac{(y-4)^2}{25}=1$

Jibu

$\dfrac{(x-2)^2}{7^2}+\dfrac{(y-4)^2}{5^2}=1$; Endpoints ya mhimili mkubwa$(9,4)$,$(-5,4)$. Mwisho wa mhimili mdogo$(2,9)$,$(2,-1)$. Foci katika$(2+2\sqrt{6}, 4)$,$(2-2\sqrt{6}, 4)$

16)$\dfrac{(x-2)^2}{81}+\dfrac{(y+1)^2}{16}=1$

17)$\dfrac{(x+5)^2}{4}+\dfrac{(y-7)^2}{9}=1$

Jibu

$\dfrac{(x+5)^2}{2^2}+\dfrac{(y-7)^2}{3^2}=1$; Endpoints ya mhimili mkubwa$(-5,10)$,$(-5,4)$. Mwisho wa mhimili mdogo$(-3,7)$,$(-7,7)$. Foci katika$(-5, 7+\sqrt{5})$,$(-5, 7-\sqrt{5})$

18)$\dfrac{(x-7)^2}{49}+\dfrac{(y-7)^2}{49}=1$

19)$4x^2-8x+9y^2-72y+112=0$

Jibu

$\dfrac{(x-1)^2}{3^2}+\dfrac{(y-4)^2}{2^2}=1$; Endpoints ya mhimili mkubwa$(4,4)$,$(-2,4)$. Mwisho wa mhimili mdogo$(1,6)$,$(1,2)$. Foci katika$(1+\sqrt{5}, 4)$,$(1-\sqrt{5}, 4)$

20)$9x^2-54x+9y^2-54y+81=0$

21)$4x^2-24x+36y^2-360y+864=0$

Jibu

$\dfrac{(x-3)^2}{(3\sqrt{2})^2}+\dfrac{(y-5)^2}{\sqrt{2}^2}=1$; Endpoints ya mhimili mkubwa$(3+3\sqrt{2}, 5)$,$(3-3\sqrt{2}, 5)$. Mwisho wa mhimili mdogo$(3, 5+\sqrt{2})$,$(3, 5-\sqrt{2})$. Foci katika$(7,5)$,$(-1,5)$

22)$4x^2+24x+16y^2-128y+228=0$

23)$4x^2+40x+25y^2-100y+100=0$

Jibu

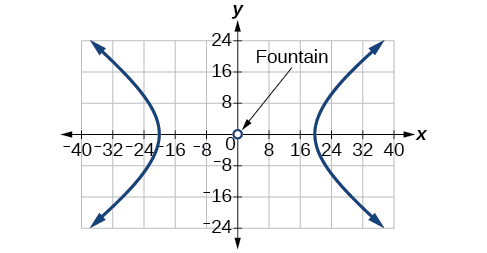
$\dfrac{(x+5)^2}{(5)^2}+\dfrac{(y-2)^2}{(2)^2}=1$; Endpoints ya mhimili mkubwa$(0,2)$,$(-10,2)$. Mwisho wa mhimili mdogo$(-5,4)$,$(-5,0)$. Foci katika$(-5+\sqrt{21}, 2)$,$(-5-\sqrt{21}, 2)$

24)$x^2+2x+100y^2-1000y+2401=0$

25)$4x^2+24x+25y^2+200y+336=0$

Jibu

$\dfrac{(x+3)^2}{(5)^2}+\dfrac{(y+4)^2}{(2)^2}=1$; Endpoints ya mhimili mkubwa$(2,-4)$,$(-8,-4)$. Mwisho wa mhimili mdogo$(-3,-2)$,$(-3,-6)$. Foci katika$(-3+\sqrt{21}, -4)$,$(-3-\sqrt{21}, -4)$

26)$9x^2+72x+16y^2+16y+4=0$

Kwa mazoezi 27-31, tafuta foci kwa ellipses iliyotolewa.

27)$\dfrac{(x+3)^2}{25}+\dfrac{(y+1)^2}{36}=1$

Jibu

Foci$(-3, -1+\sqrt{11})$,$(-3, -1-\sqrt{11})$

28)$\dfrac{(x+1)^2}{100}+\dfrac{(y-2)^2}{4}=1$

29)$x^2+y^2=1$

Jibu

Focus$(0,0)$

30)$x^2+4y^2+4x+8y=1$

31)$10x^2+y^2+200x=0$

Jibu

Foci$(-10,30)$,$(-10,-30)$

Graphic

Kwa mazoezi 32-45, graph ellipses iliyotolewa, akibainisha kituo, vertices, na foci.

32)$\dfrac{x^2}{25}+\dfrac{y^2}{36}=1$

33)$\dfrac{x^2}{16}+\dfrac{y^2}{9}=1$

Jibu

Kituo cha$(0,0)$, vipeo$(4,0)$$(-4,0)$,$(0,3)$,$(0,-3)$. Foci$(\sqrt{7},0)$,$(-\sqrt{7},0)$

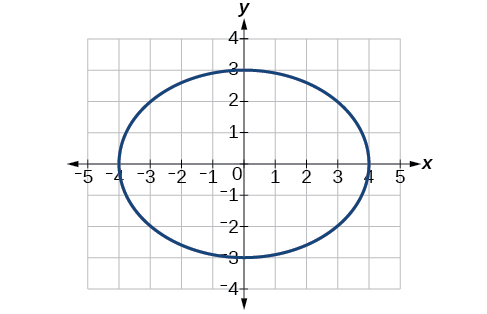
34)$4x^2+9y^2=1$

35)$81x^2+49y^2=1$

Jibu

Kituo cha$(0,0)$, vipeo$\left ( \dfrac{1}{9}, 0 \right )$$\left ( -\dfrac{1}{9}, 0 \right )$,$\left ( 0, \dfrac{1}{7} \right )$,$\left ( 0, \dfrac{1}{7} \right )$. Foci$\left ( 0, \dfrac{4\sqrt{2}}{63} \right )$,$\left ( 0, -\dfrac{4\sqrt{2}}{63} \right )$

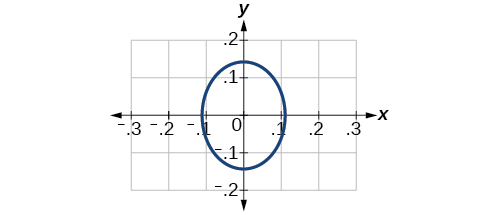
36)$\dfrac{(x-2)^2}{64}+\dfrac{(y-4)^2}{16}=1$

37)$\dfrac{(x+3)^2}{9}+\dfrac{(y-3)^2}{9}=1$

Jibu

Kituo cha$(-3,3)$, vipeo$(0,3)$$(-6,3)$,$(-3,0)$,$(-3,6)$. Focus$(-3,3)$

Kumbuka kwamba duaradufu hii ni mduara. Mzunguko una lengo moja tu, linalofanana na kituo.

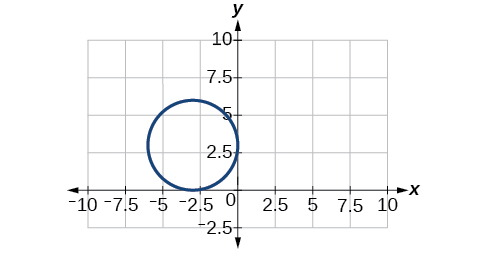
38)$\dfrac{x^2}{2}+\dfrac{(y+1)^2}{5}=1$

39)$4x^2-8x+16y^2-32y-44=0$

Jibu

Kituo cha$(1,1)$, vipeo$(5,1)$$(-3,1)$,$(1,3)$,$(1,-1)$. Foci$(1,1+4\sqrt{3})$,$(1,1-4\sqrt{3})$

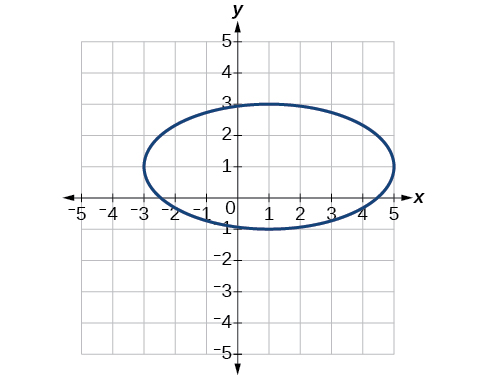
40)$x^2-8x+25y^2-100y+91=0$

41)$x^2+8x+4y^2-40y+112=0$

Jibu

Kituo cha$(-4,5)$, vipeo$(-2,5)$$(-6,4)$,$(-4,6)$,$(-4,4)$. Foci$(-4+\sqrt{3}, 5)$,$(-4-4\sqrt{3}, 5)$

42)$64x^2+128x+9y^2-72y-368=0$

43)$16x^2+64x+4y^2-8y+4=0$

Jibu

Kituo cha$(-2,1)$, vipeo$(0,1)$$(-4,1)$,$(-2,5)$,$(-2,-3)$. Foci$(-2,1+2\sqrt{3})$,$(-2,1-2\sqrt{3})$

44)$100x^2+1000x+y^2-10y+2425=0$

45)$4x^2+16x+4y^2+16y+16=0$

Jibu

Kituo cha$(-2,2)$, vipeo$(0,-2)$$(-4,-2)$,$(-2,0)$,$(-2,-4)$. Focus$(-2,-2)$

Kwa mazoezi 46-51, tumia taarifa iliyotolewa kuhusu grafu ya kila duaradufu ili kuamua usawa wake.

46) Kituo cha asili, ulinganifu kwa heshima na$x$ - na$y$ -axes, kuzingatia$(4,0)$ na kumweka kwenye grafu$(0,3)$.

47) Kituo cha asili, ulinganifu kwa heshima na$x$ - na$y$ -axes, kuzingatia$(0,-2)$ na kumweka kwenye grafu$(5,0)$.

Jibu

$\dfrac{x^2}{25}+\dfrac{y^2}{29}=1$

48) Kituo cha asili, ulinganifu kwa heshima na$x$ - na$y$ -axes, kuzingatia$(3,0)$, na mhimili mkubwa ni mara mbili kwa muda mrefu kama mhimili mdogo.

49) Kituo$(4,2)$; vertex$(9,2)$; lengo moja:$(4+2\sqrt{6}, 2)$

Jibu

$\dfrac{(x-4)^2}{25}+\dfrac{(y-2)^2}{1}=1$

50) Kituo$(3,5)$; vertex$(3,11)$; lengo moja:$(3, 5+4\sqrt{2})$

51) Kituo$(-3,4)$; vertex$(1,4)$; lengo moja:$(-3+2\sqrt{3}, 4)$

Jibu

$\dfrac{(x+3)^2}{16}+\dfrac{(y-4)^2}{4}=1$

Kwa mazoezi 52-56, kutokana na grafu ya ellipse, tambua usawa wake.

52)

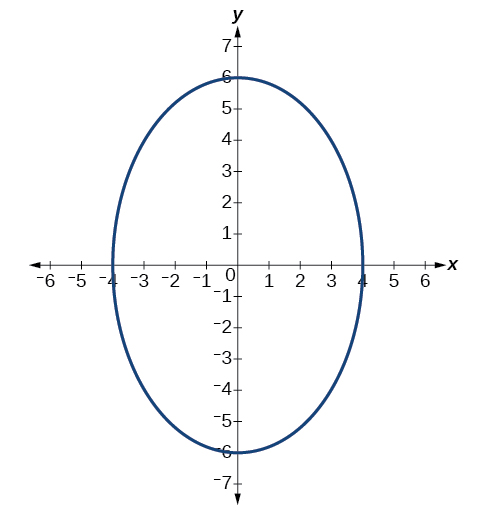
53)

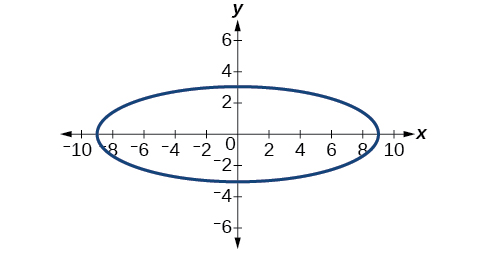
Jibu

$\dfrac{x^2}{81}+\dfrac{y^2}{9}=1$

54)

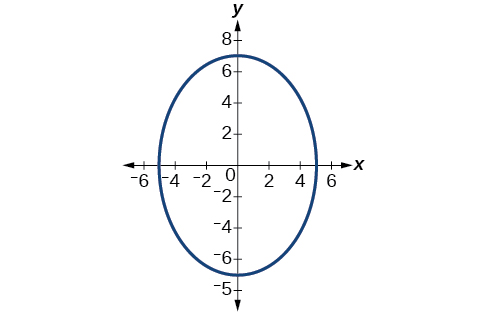
55)

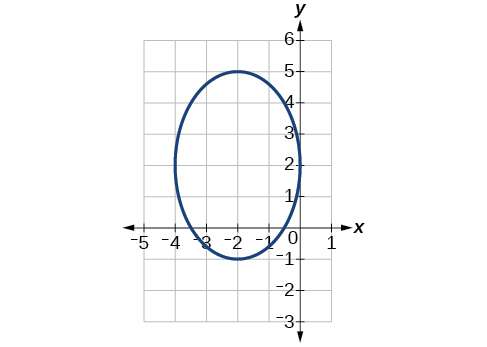
Jibu

$\dfrac{(x+2)^2}{4}+\dfrac{(y-2)^2}{9}=1$

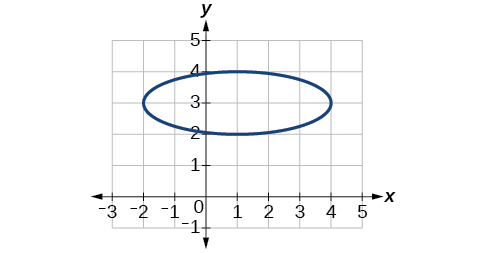
56)

Upanuzi

Kwa mazoezi 57-61, tafuta eneo la ellipse. Eneo la ellipse linatolewa na formula$\text {Area}=a\cdot b\cdot \pi$

57)$\dfrac{(x-3)^2}{9}+\dfrac{(y-3)^2}{16}=1$

Jibu

$\text {Area} = 12\pi$vitengo vya mraba

58)$\dfrac{(x+6)^2}{16}+\dfrac{(y-6)^2}{36}=1$

59)$\dfrac{(x+1)^2}{4}+\dfrac{(y-2)^2}{5}=1$

Jibu

$\text {Area} = 2\sqrt{5} \pi$vitengo vya mraba

60)$4x^2-8x+9y^2-72y+112=0$

61)$9x^2-54x+9y^2-54y+81=0$

Jibu

$\text {Area} = 9\pi$vitengo vya mraba

Real-World Matumizi

62) Kupata equation ya duaradufu kwamba tu fit ndani ya sanduku yaani$8$ vitengo pana na$4$ vitengo juu.

63) Pata equation ya duaradufu ambayo inafaa tu ndani ya sanduku ambayo ni mara nne pana kama ilivyo juu. Express katika suala la$h$, urefu.

Jibu

$\dfrac{x^2}{4h^2}+\dfrac{y^2}{\tfrac{1}{4}h^2}=1$

64) Arch ina sura ya nusu-ellipse (nusu ya juu ya ellipse). Arch ina urefu wa$8$ miguu na muda wa$20$ miguu. Pata equation kwa duaradufu, na uitumie ili kupata urefu kwa$0.01$ mguu wa karibu wa arch umbali wa$4$ miguu kutoka katikati.

65) Arch ina sura ya nusu-ellipse. Arch ina urefu wa$12$ miguu na muda wa$40$ miguu. Kupata equation kwa duaradufu, na kutumia kwamba kupata umbali kutoka katikati ya hatua ambayo urefu ni$6$ miguu. Pande zote hadi karibu na mia moja.

Jibu

$\dfrac{x^2}{400}+\dfrac{y^2}{144}=1$. Umbali =$17.32$ miguu

66) Daraja ni kujengwa kwa sura ya arch nusu-elliptical na ni kuwa na muda wa$120$ miguu. Urefu wa arch umbali wa$40$ miguu kutoka katikati ni kuwa$8$ miguu. Pata urefu wa arch katikati yake.

67) Mtu katika nyumba ya sanaa ya whispering amesimama kwenye mtazamo mmoja wa duaradufu anaweza kuongea na kusikilizwa na mtu amesimama kwenye mwelekeo mwingine kwa sababu mawimbi yote ya sauti ambayo yanafikia dari yanajitokeza kwa mtu mwingine. Ikiwa nyumba ya sanaa ya whispering ina urefu wa$120$$30$ miguu, na foci iko miguu kutoka katikati, pata urefu wa dari katikati.

Jibu

Takriban$51.96$ miguu

68) Mtu amesimama$8$ miguu kutoka ukuta wa karibu katika nyumba ya sanaa ya whispering. Kama mtu huyo ni katika lengo moja, na lengo nyingine ni$80$ miguu mbali, ni nini urefu na urefu katika kituo cha nyumba ya sanaa?

10.2: Hyperbola

Katika jiometri ya uchambuzi, hyperbola ni sehemu ya conic inayoundwa na kuingiliana koni ya mviringo ya mviringo na ndege kwa pembe kama vile nusu zote za koni zimeunganishwa. Mfululizo huu hutoa curves mbili tofauti zisizo na mipaka ambazo ni picha za kioo za kila mmoja.

Maneno

1) Kufafanua hyperbola kwa suala la foci yake.

Jibu

Hyperbola ni seti ya pointi katika ndege tofauti ya umbali wake kutoka pointi mbili fasta (foci) ni mara kwa mara chanya.

2) Tunaweza kuhitimisha nini kuhusu hyperbola ikiwa asymptotes yake inakabiliana na asili?

3) Ni lazima iwe kweli kwa foci ya hyperbola?

Jibu

The foci lazima uongo juu ya mhimili transverse na kuwa katika mambo ya ndani ya hyperbola.

4) Ikiwa mhimili wa hyperbola ni wima, tunajua nini kuhusu grafu?

5) Je, katikati ya hyperbola lazima iwe wapi na foci yake?

Jibu

Kituo hicho lazima kiwe katikati ya sehemu ya mstari kujiunga na foci.

Kialjebra

Kwa mazoezi 6-10, onyesha kama equations zifuatazo zinawakilisha hyperbolas. Ikiwa ndivyo, andika kwa fomu ya kawaida.

6)$3y^2 + 2x = 6$

7)$\dfrac{x^2}{36}-\dfrac{y^2}{9}=1$

Jibu

ndiyo$\dfrac{x^2}{6^2}-\dfrac{y^2}{3^2}=1$

8)$5y^2 + 4x^2 = 6x$

9)$25x^2 - 16y^2 = 400$

Jibu

ndiyo$\dfrac{x^2}{4^2}-\dfrac{y^2}{5^2}=1$

10)$-9x^2+18x+y^2+4y-14=0$

Kwa mazoezi 11-25, andika equation kwa hyperbola kwa fomu ya kawaida ikiwa haijawahi, na kutambua vipeo na foci, na uandike equations ya asymptotes.

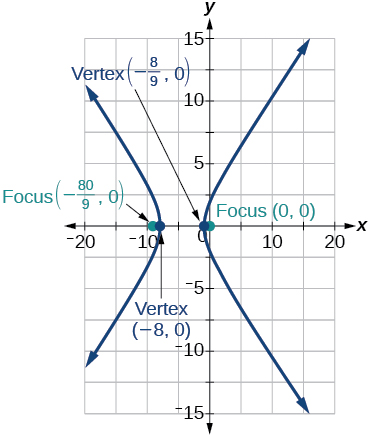
11)$\dfrac{x^2}{25}-\dfrac{y^2}{36}=1$

Jibu

$\dfrac{x^2}{5^2}-\dfrac{y^2}{6^2}=1$; vertices:$(5,0)$,$(-5,0)$; foci:$(\sqrt{61},0)$,$(-\sqrt{61},0)$; asymptotes:$y=\dfrac{6}{5}x$,$y=-\dfrac{6}{5}x$

12)$\dfrac{x^2}{100}-\dfrac{y^2}{9}=1$

13)$\dfrac{y^2}{4}-\dfrac{x^2}{81}=1$

Jibu

$\dfrac{y^2}{2^2}-\dfrac{x^2}{9^2}=1$; vertices:$(0,2)$,$(0,-2)$; foci:$(0,\sqrt{85})$,$(0,-\sqrt{85})$; asymptotes:$y=\dfrac{2}{9}x$,$y=-\dfrac{2}{9}x$

14)$9y^2 - 4x^2 = 1$

15)$\dfrac{(x-1)^2}{9}-\dfrac{(y-2)^2}{16}=1$

Jibu

$\dfrac{(x-1)^2}{3^2}-\dfrac{(y-2)^2}{4^2}=1$; vertices:$(4,2)$,$(-2,2)$; foci:$(6,2)$,$(-4,2)$; asymptotes:$y=\dfrac{4}{3}(x-1)+2$,$y=-\dfrac{4}{3}(x-1)+2$

16)$\dfrac{(y-6)^2}{36}-\dfrac{(x+1)^2}{16}=1$

17)$\dfrac{(x-2)^2}{49}-\dfrac{(y+7)^2}{49}=1$

Jibu

$\dfrac{(x-2)^2}{7^2}-\dfrac{(y+7)^2}{7^2}=1$; vertices:$(9,-7)$,$(-5,-7)$; foci:$(2+7\sqrt{2},-7)$,$(2-7\sqrt{2},-7)$; asymptotes:$y=x-9$,$y=-x-5$

18)$4x^2-8x-9y^2-72y+112=0$

19)$-9x^2-54x+9y^2-54y+81=0$

Jibu

$\dfrac{(x+3)^2}{3^2}-\dfrac{(y-3)^2}{3^2}=1$; vertices:$(0,3)$,$(-6,3)$; foci:$(-3+3\sqrt{2},1)$,$(-3-3\sqrt{2},1)$; asymptotes:$y=x+6$,$y=-x$

20)$4x^2-24x-36y^2-360y+864=0$

21)$-4x^2+24x+16y^2-128y+156=0$

Jibu

$\dfrac{(y-4)^2}{2^2}-\dfrac{(x-3)^2}{4^2}=1$; vertices:$(3,6)$,$(3,2)$; foci:$(3,4+2\sqrt{5})$,$(3,4-2\sqrt{5})$; asymptotes:$y=\dfrac{1}{2}(x-3)+4$,$y=-\dfrac{1}{2}(x-3)+4$

22)$-4x^2+40x+25y^2-100y+100=0$

23)$x^2+2x-100y^2-1000y+2401=0$

Jibu

$\dfrac{(y+5)^2}{7^2}-\dfrac{(x+1)^2}{70^2}=1$; vertices:$(-1,2)$,$(-1,-12)$; foci:$(-1,-5+7\sqrt{101})$,$(-1,-5-7\sqrt{101})$; asymptotes:$y=\dfrac{1}{10}(x+1)-5$,$y=-\dfrac{1}{10}(x+1)-5$

24)$-9x^2+72x+16y^2+16y+4=0$

25)$4x^2+24x-25y^2+200y-464=0$

Jibu

$\dfrac{(x+3)^2}{5^2}-\dfrac{(y-4)^2}{2^2}=1$; vertices:$(2,4)$,$(-8,4)$; foci:$(-3+\sqrt{29},4)$,$(-3-\sqrt{29},4)$; asymptotes:$y=\dfrac{2}{5}(x+3)+4$,$y=-\dfrac{2}{5}(x+3)+4$

Kwa mazoezi 26-30, pata usawa wa asymptotes kwa kila hyperbola.

26)$\dfrac{y^2}{3^2}-\dfrac{x^2}{3^2}=1$

27)$\dfrac{(x-3)^2}{5^2}-\dfrac{(y+4)^2}{2^2}=1$

Jibu

$y=\dfrac{2}{5}(x-3)-4$,$y=-\dfrac{2}{5}(x-3)-4$

28)$\dfrac{(y-3)^2}{3^2}-\dfrac{(x+5)^2}{6^2}=1$

29)$9x^2-18x-16y^2+32y-151=0$

Jibu

$y=\dfrac{3}{4}(x-1)+1$,$y=-\dfrac{3}{4}(x-1)+1$

30)$16y^2+96y-4x^2+16x+112=0$

Graphic

Kwa mazoezi ya 31-44, mchoro grafu ya hyperbola, alama za kuandika na foci.

31)$\dfrac{x^2}{49}-\dfrac{y^2}{16}=1$

Jibu

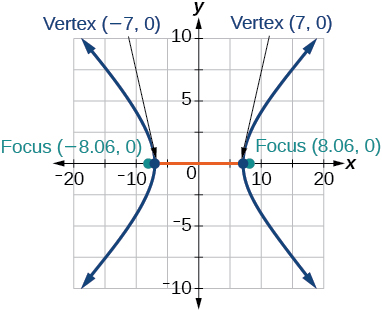
32)$\dfrac{x^2}{64}-\dfrac{y^2}{4}=1$

33)$\dfrac{y^2}{9}-\dfrac{x^2}{25}=1$

Jibu

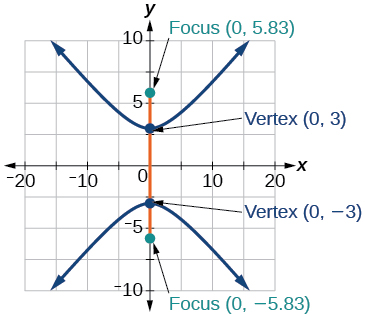
34)$81x^2-9y^2=1$

35)$\dfrac{(y+5)^2}{9}-\dfrac{(x-4)^2}{25}=1$

Jibu

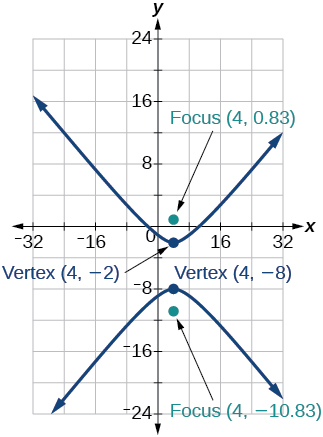
36)$\dfrac{(x-2)^2}{8}-\dfrac{(y+3)^2}{27}=1$

37)$\dfrac{(y-3)^2}{9}-\dfrac{(x-3)^2}{9}=1$

Jibu

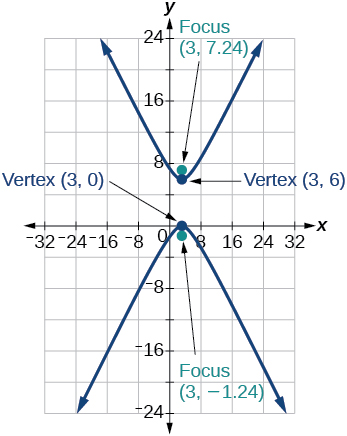
38)$-4x^2-8x+16y^2-32y-52=0$

39)$x^2-8x-25y^2-100y-109=0$

Jibu

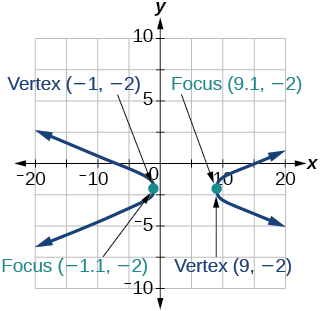
40)$-x^2+8x+4y^2-40y+88=0$

41)$64x^2+128x-9y^2-72y-656=0$

Jibu

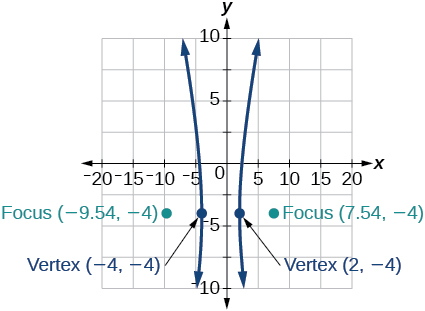
42)$16x^2+64x-4y^2-8y-4=0$

43)$-100x^2+1000x+y^2-10y-2575=0$

Jibu

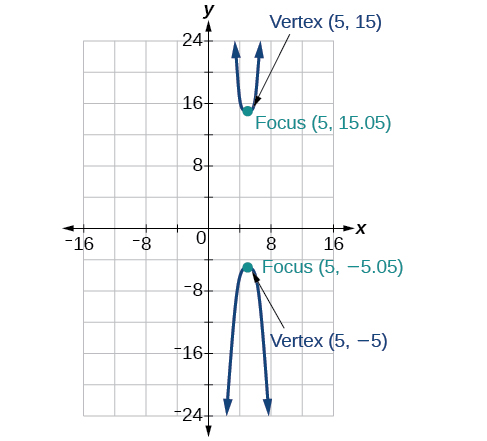
44)$4x^2+16x-4y^2+16y+16=0$

Kwa mazoezi 45-50, kutokana na taarifa kuhusu grafu ya hyperbola, pata equation yake.

45) Vertices katika$(3,0)$$(-3,0)$ na na lengo moja katika$(5,0)$.

Jibu

$\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$

46) Vertices katika$(0,6)$$(0,-6)$ na na lengo moja katika$(0,-8)$.

47) Vertices katika$(1,1)$$(11,1)$ na na lengo moja katika$(12,1)$.

Jibu

$\dfrac{(x-6)^2}{25}-\dfrac{(y-1)^2}{11}=1$

48) Kituo cha:$(0,0)$; vertex:$(0,-13)$;lengo moja:$(0,\sqrt{313})$.

49) Kituo cha:$(4,2)$; vertex:$(9,2)$;lengo moja:$(4+\sqrt{26},2)$.

Jibu

$\dfrac{(x-4)^2}{25}-\dfrac{(y-2)^2}{1}=1$

50) Center:$(3,5)$; kipeo:$(3,11)$; lengo moja:$(3,5+2\sqrt{10})$.

Kwa mazoezi 51-,55 kutokana na grafu ya hyperbola, pata equation yake.

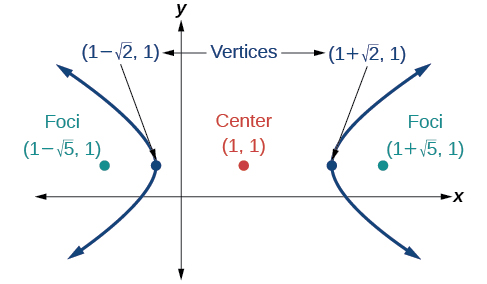
51)

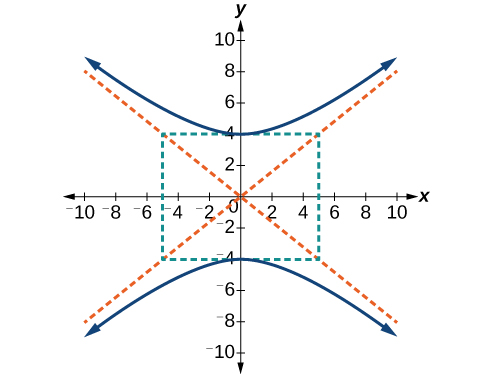
Jibu

$\dfrac{y^2}{16}-\dfrac{x^2}{25}=1$

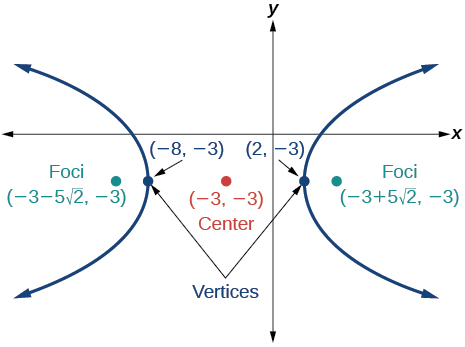
52)

53)

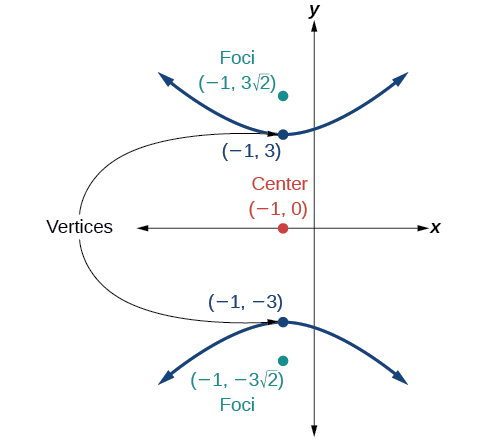
Jibu

$\dfrac{y^2}{9}-\dfrac{(x+1)^2}{9}=1$

54)

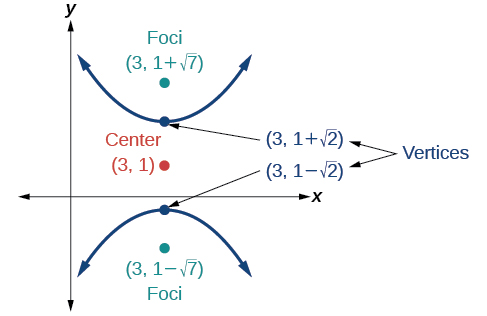
55)

Jibu

$\dfrac{(x+3)^2}{25}-\dfrac{(y+3)^2}{25}=1$

Upanuzi

Kwa mazoezi 56-60, kueleza equation kwa hyperbola kama kazi mbili, na$y$ kama kazi ya$x$. Eleza kama iwezekanavyo. Tumia calculator ya graphing ili mchoro grafu ya kazi mbili kwenye shaba sawa.

56)$\dfrac{x^2}{4}-\dfrac{y^2}{9}=1$

57)$\dfrac{y^2}{9}-\dfrac{x^2}{1}=1$

Jibu

$y(x)=3\sqrt{x^2 +1}$,$y(x)=-3\sqrt{x^2 +1}$

58)$\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{25}=1$

59)$-4x^2-16x+y^2-2y-19=0$

Jibu

$y(x)=1+2\sqrt{x^2 +4x+5}$,$y(x)=1-2\sqrt{x^2 +4x+5}$

60)$4x^2-24x-y^2-4y+16=0$

Real-World Matumizi

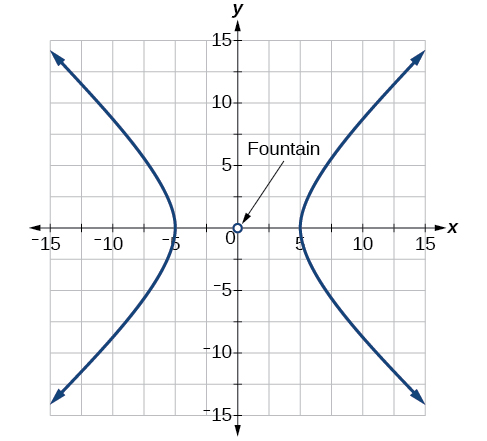
Kwa mazoezi 61-65, ua unapaswa kujengwa kwa sura ya hyperbola karibu na chemchemi katikati ya yadi. Pata equation ya hyperbola na mchoro grafu.

61) Ua utafuata asymptotes$y=x$ na$y=-x$, na umbali wake wa karibu na chemchemi ya katikati ni$5$ yadi.

Jibu

$\dfrac{x^2}{25}-\dfrac{y^2}{25}=1$

62) Ua utafuata asymptotes$y=2x$ na$y=-2x$, na umbali wake wa karibu na chemchemi ya katikati ni$6$ yadi.

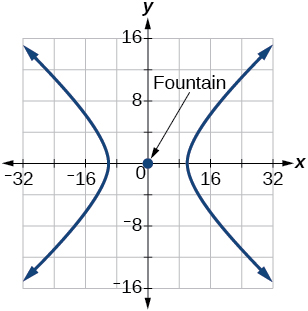
63) ua utafuata asymptotes$y=\dfrac{1}{2}x$ na$y=-\dfrac{1}{2}x$, na umbali wake wa karibu na chemchemi ya kituo ni$10$ yadi.

Jibu

$\dfrac{x^2}{100}-\dfrac{y^2}{25}=1$

64) Ua utafuata asymptotes$y=\dfrac{2}{3}x$ na$y=-\dfrac{2}{3}x$, na umbali wake wa karibu na chemchemi ya katikati ni$12$ yadi.

65) Ua utafuata asymptotes$y=\dfrac{3}{4}x$ na$y=-\dfrac{3}{4}x$, na umbali wake wa karibu na chemchemi ya katikati ni$20$ yadi.

Jibu

$\dfrac{x^2}{400}-\dfrac{y^2}{225}=1$

Kwa mazoezi 66-70, kudhani kitu kinaingia mfumo wetu wa jua na tunataka kuchora njia yake kwenye mfumo wa kuratibu na jua kwenye asili na$x$ -axis kama mhimili wa ulinganifu kwa njia ya kitu. Kutoa equation ya njia ya ndege ya kila kitu kwa kutumia taarifa iliyotolewa.

66) Kitu kinaingia kwenye njia inayofikiriwa$y=x-2$ na mstari na hupita ndani ya$1$ au (kitengo cha astronomical) cha jua kwa njia yake ya karibu, ili jua liwe lengo moja la hyperbola. Halafu huondoka mfumo wa jua kwenye njia inayokadiriwa na mstari$y=−x+2$.

67) Kitu kinaingia kwenye njia inayofikiriwa$y=2x-2$ na mstari na hupita ndani ya$0.5$ au ya jua kwa njia yake ya karibu, hivyo jua ni lengo moja la hyperbola. Halafu huondoka mfumo wa jua kwenye njia inayokadiriwa na mstari$y=-2x+2$.

Jibu

$\dfrac{(x-1)^2}{0.25}-\dfrac{y^2}{0.75}=1$

68) Kitu kinaingia kwenye njia inayofikiriwa$y=0.5x+2$ na mstari na hupita ndani ya$1$ au ya jua kwa njia yake ya karibu, hivyo jua ni lengo moja la hyperbola. Halafu huondoka mfumo wa jua kwenye njia inayokadiriwa na mstari$y=−0.5x−2$.

69) Kitu kinaingia kwenye njia inayofikiriwa$y=\dfrac{1}{3}x-1$ na mstari na hupita ndani ya$1$ au ya jua kwa njia yake ya karibu, hivyo jua ni lengo moja la hyperbola. Halafu huondoka mfumo wa jua kwenye njia inayokadiriwa na mstari$y=-\dfrac{1}{3}x+1$.

Jibu

$(x-3)^2 - 9y^2 = 4$

70) Kitu kinaingia kwenye njia inayofikiriwa$y=3x-9$ na mstari na hupita ndani ya$1$ au ya jua kwa njia yake ya karibu, hivyo jua ni lengo moja la hyperbola. Halafu huondoka mfumo wa jua kwenye njia inayokadiriwa na mstari$y=−3x+9$.

10.3: Parabola

Kama duaradufu na hyperbola, parabola pia inaweza kuelezwa na seti ya pointi katika ndege ya kuratibu. Parabola ni seti ya pointi zote katika ndege ambayo ni umbali sawa kutoka kwenye mstari uliowekwa, unaoitwa directrix, na hatua ya kudumu (lengo) sio kwenye directrix.

Maneno

1) Kufafanua parabola katika suala la lengo lake na directrix.

Jibu

Parabola ni seti ya pointi katika ndege ambayo hulala equidistant kutoka hatua fasta, lengo, na mstari fasta, directrix.

2) Ikiwa equation ya parabola imeandikwa kwa fomu ya kawaida na$p$ ni chanya na directrix ni mstari wa wima, basi tunaweza kuhitimisha nini kuhusu grafu yake?

3) Ikiwa equation ya parabola imeandikwa kwa fomu ya kawaida na$p$ ni hasi na directrix ni mstari usio na usawa, basi tunaweza kuhitimisha kuhusu grafu yake?

Jibu

Grafu itafungua.

4) Ni nini athari juu ya grafu ya parabola kama equation yake katika hali ya kiwango ina kuongeza maadili ya$p$?

5) Kama grafu ya parabola inakuwa pana, nini kitatokea kwa umbali kati ya lengo na directrix?

Jibu

Umbali kati ya lengo na directrix itaongezeka.

Kialjebra

Kwa mazoezi 6-10, onyesha kama equation iliyotolewa ni parabola. Ikiwa ndivyo, andika upya equation katika fomu ya kawaida.

6)$y^2=4-x^2$

7)$y=4x^2$

Jibu

ndiyo$y=4(1)x^2$

8)$3x^2-6y^2=12$

9)$(y-3)^2=8(x-2)$

Jibu

ndiyo$(y-3)^2=4(2)(x-2)$

10)$y^2+12x-6y-51=0$

Kwa mazoezi 11-30, andika upya equation iliyotolewa kwa fomu ya kawaida, na kisha uamua kipeo$(V)$, lengo$(F)$, na directrix$(d)$ ya parabola.

11)$x=8y^2$

Jibu

$y^2=\dfrac{1}{8}x$,$V:(0,0)$,$F:\left (\dfrac{1}{32},0 \right )$,$d:x=-\dfrac{1}{32}$

12)$y=\dfrac{1}{4}x^2$

13)$y=-4x^2$

Jibu

$x^2=-\dfrac{1}{4}y$,$V:(0,0)$,$F:\left (0,-\dfrac{1}{16} \right )$,$d:y=-\dfrac{1}{16}$

14)$x=\dfrac{1}{8}y^2$

15)$x=36y^2$

Jibu

$y^2=\dfrac{1}{36}x$,$V:(0,0)$,$F:\left (\dfrac{1}{144},0 \right )$,$d:x=-\dfrac{1}{144}$

16)$x=\dfrac{1}{36}y^2$

17)$(x-1)^2=4(y-1)$

Jibu

$(x-1)^2=4(y-1)$,$V:(1,1)$,$F:(1,2)$,$d:y=0$

18)$(y-2)^2=\dfrac{4}{5}(x+4)$

19)$(y-4)^2=2(x+3)$

Jibu

$(y-4)^2=2(x+3)$,$V:(-3,4)$,$F:\left (-\dfrac{5}{2},4 \right )$,$d:x=-\dfrac{7}{2}$

20)$(x+1)^2=2(y+4)$

21)$(x+4)^2=24(y+1)$

Jibu

$(x+4)^2=24(y+1)$,$V:(-4,-1)$,$F:(-4,5)$,$d:y=-7$

22)$(y+4)^2=16(x+4)$

23)$y^2+12x-6y+21=0$

Jibu

$(y-3)^2=-12(x+1)$,$V:(-1,3)$,$F:(-4,3)$,$d:x=2$

24)$x^2-4x-24y+28=0$

25)$5x^2-50x-4y+113=0$

Jibu

$(x-5)^2=\dfrac{4}{5}(y+3)$,$V:(5,-3)$,$F:\left (5,-\dfrac{14}{5} \right )$,$d:y=-\dfrac{16}{5}$

26)$y^2-24x+4y-68=0$

27)$x^2-4x+2y-6=0$

Jibu

$(x-2)^2=-2(y-5)$,$V:(2,5)$,$F:\left (2,\dfrac{9}{2} \right )$,$d:y=\dfrac{11}{2}$

28)$y^2-6y+12x-3=0$

29)$3y^2-4x-6y+23=0$

Jibu

$(y-1)^2=\dfrac{4}{3}(x-5)$,$V:(5,1)$,$F:\left (\dfrac{16}{3},1 \right )$,$d:x=\dfrac{14}{3}$

30)$x^2+4x+8y-4=0$

Graphic

Kwa mazoezi 31-44, graph parabola, kuashiria lengo na directrix.

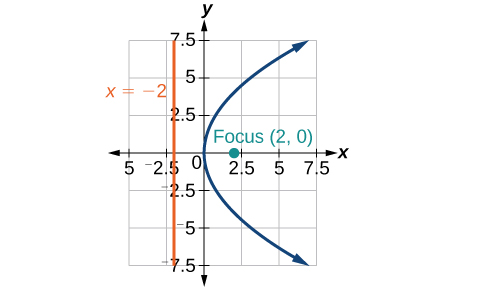
31)$x=\dfrac{1}{8}y^2$

Jibu

32)$y=36x^2$

33)$y=\dfrac{1}{36}x^2$

Jibu

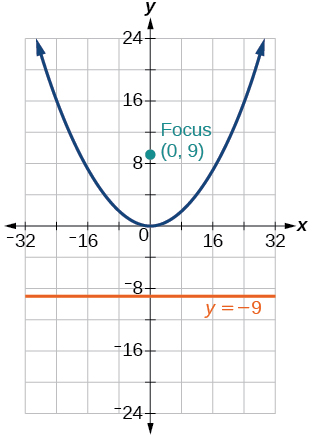
34)$y=-9x^2$

35)$(y-2)^2=-\dfrac{4}{3}(x+2)$

Jibu

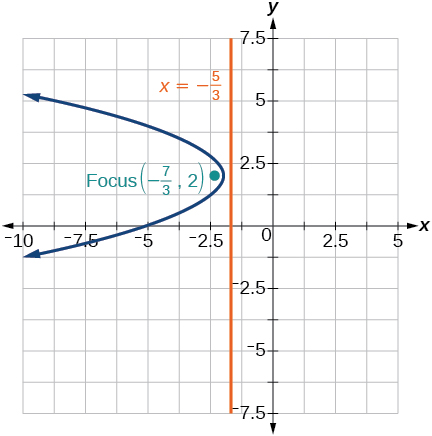
36)$-5(x+5)^2=4(y+5)$

37)$-6(y+5)^2=4(x-4)$

Jibu

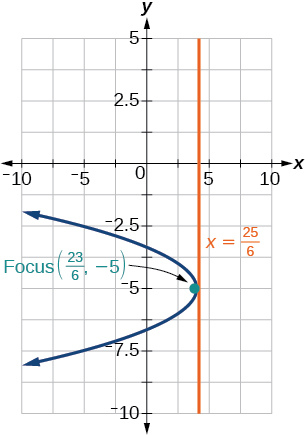
38)$y^2-6y-8x+1=0$

39)$x^2+8x+4y+20=0$

Jibu

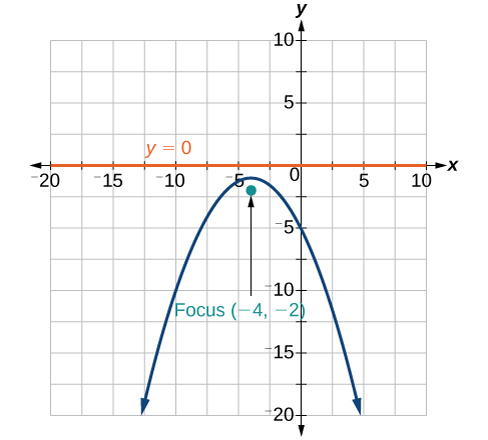
40)$3x^2+30x-4y+95=0$

41)$y^2-8x+10y+9=0$

Jibu

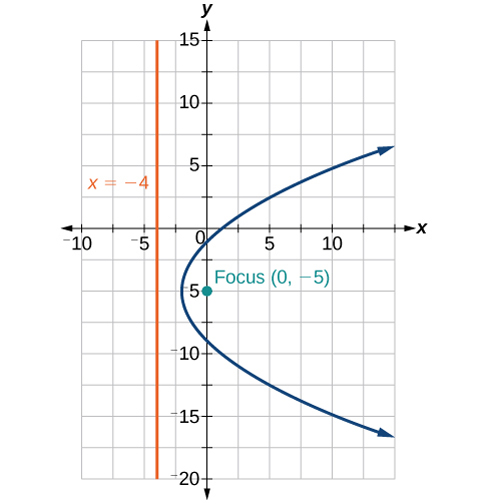
42)$x^2+4x+2y+2=0$

43)$y^2+2y-12x+61=0$

Jibu

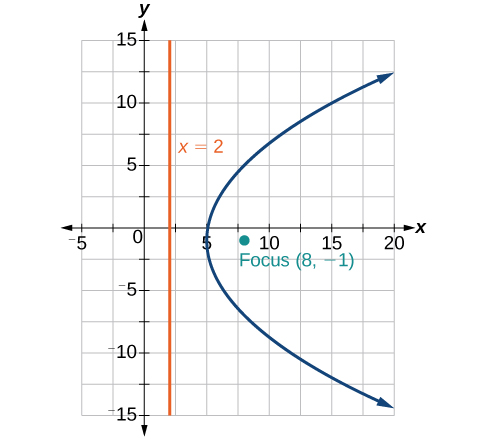
44)$-2x^2+8x-4y-24=0$

Kwa mazoezi 45-50, pata equation ya parabola iliyotolewa habari kuhusu grafu yake.

45) Vertex ni$(0,0)$; directrix ni$y=4$, lengo ni$(0,-4)$.

Jibu

$x^2=-16y$

46) Vertex ni$(0,0)$; directrix ni$x=4$, lengo ni$(-4,0)$.

47) Vertex ni$(2,2)$; directrix ni$x=2-\sqrt{2}$, lengo ni$(2+\sqrt{2},2)$.

Jibu

$(y-2)^2 = 4\sqrt{2}(x-2)$

48) Vertex ni$(-2,3)$; directrix ni$x=-\dfrac{7}{2}$, lengo ni$\left(-\dfrac{1}{2},3 \right)$.

49) Vertex ni$(\sqrt{2},-\sqrt{3})$; directrix ni$x=2\sqrt{2}$, lengo ni$(0,-\sqrt{3})$.

Jibu

$(y+\sqrt{3})^2 = -4\sqrt{2}(x-\sqrt{2})$

50) Vertex ni$(-,21)$; directrix ni$y=\dfrac{11}{3}$, lengo ni$\left(1,\dfrac{1}{3} \right)$.

Kwa mazoezi 51-55, tambua equation kwa parabola kutoka kwenye grafu yake.

51)

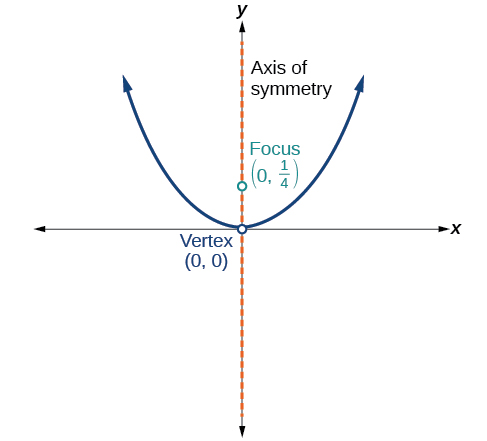
Jibu

$x^2=y$

52)

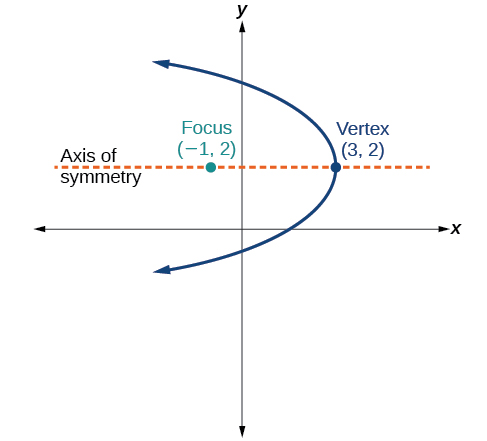
53)

Jibu

$(y-2)^2 = \dfrac{1}{4}(x+2)$

54)

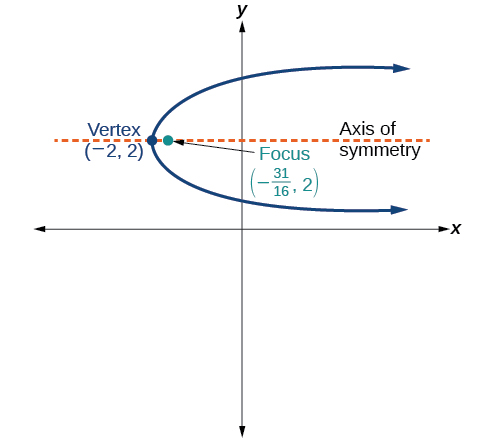
55)

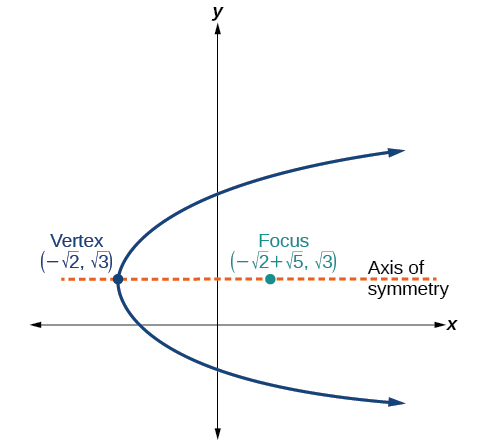
Jibu

$(y-\sqrt{2})^2 = 4\sqrt{5}(x+\sqrt{2})$

Upanuzi

Kwa mazoezi 56-60, vertex na mwisho wa rectum latus ya parabola hutolewa. Kupata equation.

56)$V(0,0)$, Mwisho$(2,1),(−2,1)$

57)$V(0,0)$, Mwisho$(-2,4),(−2,-4)$

Jibu

$y^2=-8x$

58)$V(1,2)$, Endpoints $(-5,5),(7,5)$

59)$V(-3,-1)$, Endpoints $(0,5),(0,-7)$

Jibu

$(y+1)^2 = 12(x+3)$

60)$V(4,-3)$, Endpoints $\left ( 5,-\dfrac{7}{2} \right ), \left ( 3,-\dfrac{7}{2} \right )$

Real-World Matumizi

61) Kioo katika kichwa cha gari kina sehemu ya msalaba wa parabolic na bomba la mwanga kwenye lengo. Kwa schematic, equation ya parabola inapewa kama$x^2=4y$. Je, ni kuratibu gani unapaswa kuweka bulb ya mwanga?

Jibu

$(0,1)$

62) Ikiwa tunataka kujenga kioo kutoka kwa zoezi la awali kama vile lengo liko katika$(0,0.25)$ nini lazima equation ya parabola iwe?

63) Sahani ya satelaiti imeumbwa kama paraboloid ya mapinduzi. Hii ina maana kwamba inaweza kuundwa kwa kupokezana parabola karibu na mhimili wake wa ulinganifu. Mpokeaji anapaswa kuwa iko kwenye lengo. Ikiwa sahani ni$12$ miguu kote wakati wa ufunguzi wake na$4$ miguu kina katikati yake, mpokeaji anapaswa kuwekwa wapi?

Jibu

Katika hatua ya$2.25$ miguu juu ya vertex.

64) Fikiria sahani ya satellite kutoka kwa zoezi la awali. Ikiwa sahani ni$8$ miguu kote wakati wa ufunguzi na$2$ miguu kirefu, tunapaswa mahali wapi mpokeaji?

65) Mwangaza wa utafutaji umeumbwa kama paraboloidi ya mapinduzi. Chanzo cha mwanga iko$1$ mguu kutoka msingi pamoja na mhimili wa ulinganifu. Ikiwa ufunguzi wa utafutaji ni$3$ miguu kote, pata kina.

Jibu

$0.5625$miguu

66) Ikiwa utafutaji kutoka kwa zoezi la awali lina chanzo cha mwanga kilichopo$6$ inchi kutoka msingi pamoja na mhimili wa ulinganifu na ufunguzi ni$4$ miguu, pata kina.

67) Arch iko katika sura ya parabola. Ina muda wa$100$ miguu na urefu wa$20$ miguu. Pata equation ya parabola, na ueleze urefu wa$40$ miguu ya upinde kutoka katikati.

Jibu

$x^2=-125(y-20)$, urefu ni$7.2$ miguu

68) Ikiwa arch kutoka kwa zoezi la awali ina muda wa$160$ miguu na urefu wa$40$ miguu, pata usawa wa parabola, na ueleze umbali kutoka katikati ambayo urefu ni$20$ miguu.

69) Kitu kinatarajiwa ili kufuata njia ya parabolic iliyotolewa na$y=-x^2+96x$ wapi$x$ umbali wa usawa uliosafiri kwa miguu na$y$ ni urefu. Kuamua urefu wa juu kitu kinafikia.

Jibu

$2304$miguu

70) Kwa kitu kutoka kwa zoezi la awali, kudhani njia iliyofuatiwa inatolewa na$y=-0.5x^2+80x$. Kuamua jinsi mbali pamoja na usawa kitu alisafiri kufikia urefu wa juu.

10.4: Mzunguko wa Axes

Katika sehemu zilizopita za sura hii, tuna ililenga equations fomu ya kawaida kwa sehemu nondegenerate conic. Katika sehemu hii, sisi kuhama lengo letu kwa jumla fomu equation, ambayo inaweza kutumika kwa ajili ya conic yoyote. Fomu ya jumla imewekwa sawa na sifuri, na maneno na coefficients hutolewa kwa utaratibu fulani, kama inavyoonyeshwa hapa chini.

Maneno

1) Je!$xy$ Neno hilo lina athari gani kwenye grafu ya sehemu ya conic?

Jibu

$xy$Neno husababisha mzunguko wa grafu kutokea.

2) Ikiwa equation ya sehemu ya conic imeandikwa kwa fomu$Ax^2+By^2+Cx+Dy+E=0$ na tunaweza kuhitimisha$AB=0$ nini?

3) Ikiwa equation ya sehemu ya conic imeandikwa kwa fomu$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$, na$B^2-4AC>0$, tunaweza kuhitimisha nini?

Jibu

Sehemu ya conic ni hyperbola.

4) Kutokana na equation$ax^2+4x+3y^2-12=0$, tunaweza kuhitimisha nini kama$a>0$?

5) Kwa equation thamani\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) ya$\theta$ kwamba satisfies$\cot (2\theta )=\dfrac{A-C}{B}$ inatupa habari gani?

Jibu

Inatoa angle ya mzunguko wa axes ili kuondoa$xy$ muda.

Kialjebra

Kwa mazoezi 6-17, tambua sehemu gani ya conic inawakilishwa kulingana na equation iliyotolewa.

6)$9x^2+4y^2+72x+36y-500=0$

7)$x^2-10x+4y-10=0$

Jibu

$AB=0$, parabola

8)$2x^2-2y^2+4x-6y-2=0$

9)$4x^2-y^2+8x-1=0$

Jibu

$AB=-4<0$, hyperbola

10)$4y^2-5x+9y+1=0$

11)$2x^2+3y^2-8x-12y+2=0$

Jibu

$AB=6>0$, duaradufu

12)$4x^2+9xy+4y^2-36y-125=0$

13)$3x^2+6xy+3y^2-36y-125=0$

Jibu

$B^2 - 4AC=0$, parabola

14)$-3x^2+3\sqrt{3}xy-4y^2+9=0$

15)$2x^2+4\sqrt{3}xy+6y^2-6x-3=0$

Jibu

$B^2 - 4AC=0$, parabola

16)$-x^2+4\sqrt{2}xy+2y^2-2y+1=0$

17)$8x^2+4\sqrt{2}xy+4y^2-10x+1=0$

Jibu

$B^2 - 4AC=-96<0$, duaradufu

Kwa mazoezi 18-22, pata uwakilishi mpya wa equation iliyotolewa baada ya kupokezana kupitia angle iliyotolewa.

18)$3x^2+xy+3y^2-5=0, \theta =45^{\circ}$

19)$4x^2-xy+4y^2-2=0, \theta =45^{\circ}$

Jibu

$7x'^2+9y'^2-4=0$

20)$2x^2+8xy-1=0, \theta =30^{\circ}$

21)$-2x^2+8xy+1=0, \theta =45^{\circ}$

Jibu

$3x'^2+2x'y'-5y'^2+1=0$

22)$4x^2+\sqrt{2}xy+4y^2+y+2=0, \theta =45^{\circ}$

Kwa mazoezi 23-30, onyesha angle$\theta$ ambayo itaondoa$xy$ muda na kuandika equation sambamba bila$xy$ muda.

23)$x^2+3\sqrt{3}xy+4y^2+y-2=0$

Jibu

$\theta =60^{\circ},11x'^2-y'2+\sqrt{3}x'+y'-4=0$

24)$4x^2+2\sqrt{3}xy+6y^2+y-2=0$

25)$9x^2-3\sqrt{3}xy+6y^2+4y-3=0$

Jibu

$\theta =150^{\circ},21x'^2+9y'^2+4x'-4\sqrt{3}y'-6=0$

26)$-3x^2-\sqrt{3}xy-2y^2-x=0$

27)$16x^2+24xy+9y^2+6x-6y+2=0$

Jibu

$\theta \approx 36.9^{\circ},125x'^2+6x'-42y'+10=0$

28)$x^2+4xy+4y^2+3x-2=0$

29)$x^2+4xy+y^2-2x+1=0$

Jibu

$\theta =45^{\circ},3x'^2-y'^2-\sqrt{2}x'+\sqrt{2}y'+1=0$

30)$4x^2-2\sqrt{3}xy+6y^2-1=0$

Graphic

Kwa mazoezi 31-38, mzunguko kupitia angle iliyotolewa kulingana na equation iliyotolewa. Kutoa equation mpya na graph equation awali na kuzungushwa.

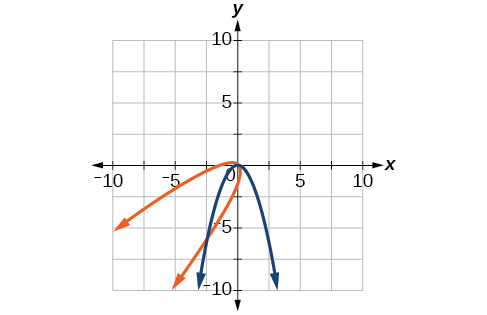
31)$y=-x^2,\theta =-45^{\circ}$

Jibu

$\dfrac{\sqrt{2}}{2}(x'+y')=\dfrac{1}{2}(x'-y')^2$

32)$x=y^2,\theta =45^{\circ}$

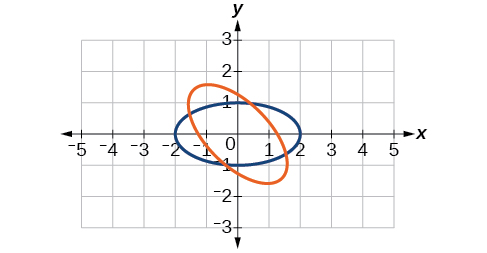
33)$\dfrac{x^2}{4}+\dfrac{y^2}{1}=1,\theta =45^{\circ}$

Jibu

$\dfrac{(x'-y')^2}{8}+\dfrac{(x'+y')^2}{2}=1$

34)$\dfrac{y^2}{16}+\dfrac{x^2}{9}=1,\theta =45^{\circ}$

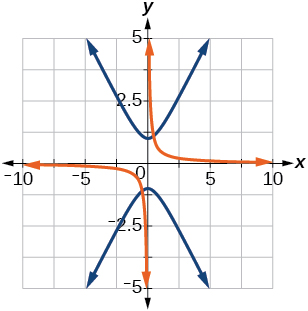
35)$y^2 - x^2 = 1, \theta =45^{\circ}$

Jibu

$\dfrac{(x'+y')^2}{2}-\dfrac{(x'-y')^2}{2}=1$

36)$y=\dfrac{x^2}{2}, \theta =30^{\circ}$

37)$x=(y-1)^2, \theta =30^{\circ}$

Jibu

$\dfrac{\sqrt{3}}{2}x'-\dfrac{1}{2}y'=\left ( \dfrac{1}{2}x' + \dfrac{\sqrt{3}}{2}x' - 1 \right )^2$

38)$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1,\theta =30^{\circ}$

Kwa mazoezi 39-49, graph equation jamaa na$x'y'$ mfumo ambao equation haina$x'y'$ muda.

39)$xy=9$

Jibu

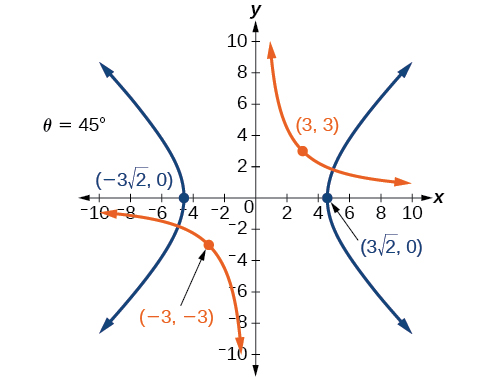
40)$x^2+10xy+y^2-6=0$

41)$x^2-10xy+y^2-24=0$

Jibu

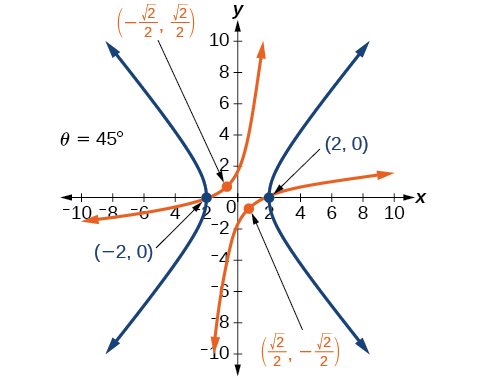
42)$4x^2-3\sqrt{3}xy+y^2-22=0$

43)$6x^2+2\sqrt{3}xy+4y^2-21=0$

Jibu

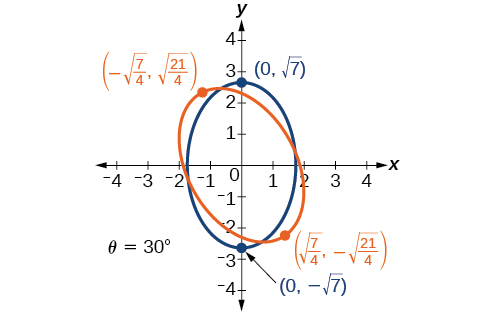
44)$11x^2+10\sqrt{3}xy+y^2-64=0$

45)$21x^2+2\sqrt{3}xy+19y^2-18=0$

Jibu

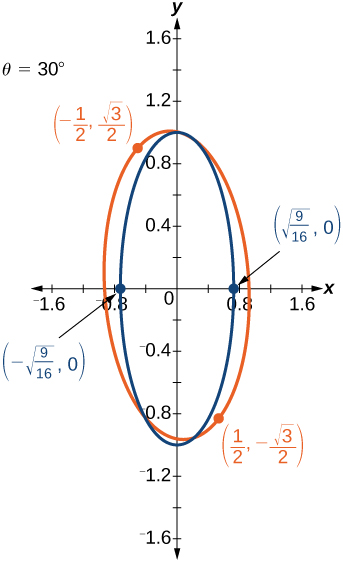
46)$16x^2+24xy+9y^2-130x+90y=0$

47)$16x^2+24xy+9y^2-60x+80y=0$

Jibu

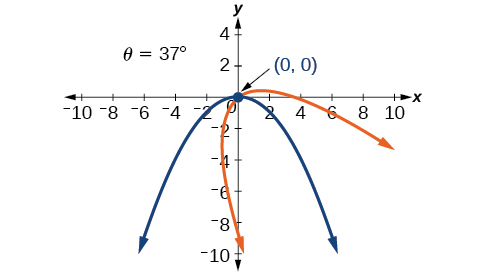
48)$13x^2-6\sqrt{3}xy+7y^2-16=0$

49)$4x^2-4xy+y^2-8\sqrt{5}x-16\sqrt{5}y=0$

Jibu

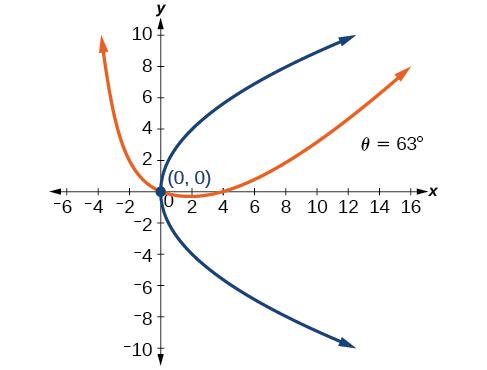
Kwa mazoezi 50-55, tambua angle ya mzunguko ili kuondoa$xy$ muda. Kisha grafu seti mpya ya axes.

50)$6x^2-5\sqrt{3}xy+y^2+10x-12y=0$

51)$6x^2-5xy+6y^2+20x-y=0$

Jibu

$\theta =45^{\circ}$

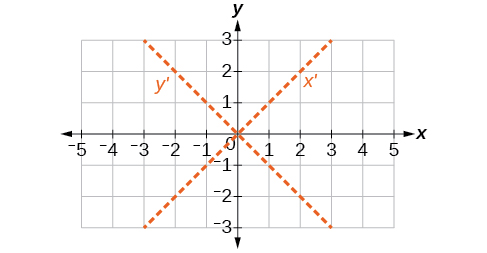
52)$6x^2-8\sqrt{3}xy+14y^2+10x-3y=0$

53)$4x^2+6\sqrt{3}xy+10y^2+20x-40y=0$

Jibu

$\theta =60^{\circ}$

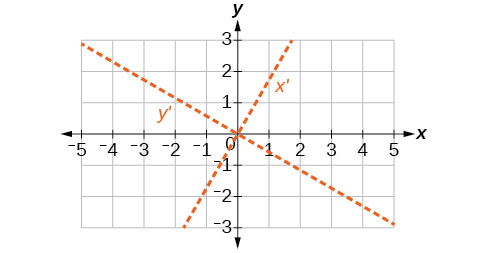
54)$8x^2+3xy+4y^2+2x-4=0$

55)$16x^2+24xy+9y^2+20x-44y=0$

Jibu

$\theta \approx 36.9^{\circ}$

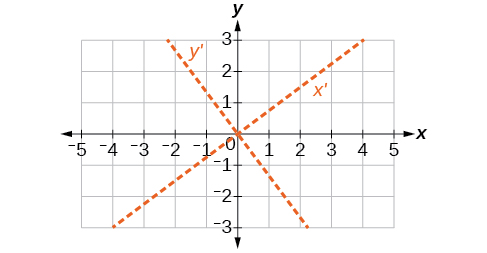
Kwa mazoezi 56-60, tambua thamani ya$k$ kulingana na equation iliyotolewa.

56) Kutokana$4x^2+kxy+16y^2+8x+24y-48=0$,$k$ tafuta kwa grafu kuwa parabola.

57) Kutokana$2x^2+kxy+12y^2+10x-16y+28=0$,$k$ tafuta grafu kuwa duaradufu.

Jibu

$-4\sqrt{6}<k<4\sqrt{6}$

58) Kutokana$3x^2+kxy+4y^2-6x+20y+128=0$,$k$ tafuta grafu kuwa hyperbola.

59) Kutokana na$kx^2+8xy+8y^2-12x+16y+18=0$ kupata$k$ kwa grafu kuwa parabola.

Jibu

$k=2$

60) Kutokana na$6x^2+12xy+ky^2+16x+10y+4=0$ kupata$k$ kwa grafu kuwa duaradufu.

10.5: Sehemu za Conic katika Kuratibu za Polar

Katika sehemu hii, tutajifunza jinsi ya kufafanua conic yoyote katika mfumo wa kuratibu wa polar kwa suala la uhakika uliowekwa, lengo la pole, na mstari, directrix, ambayo ni perpendicular kwa mhimili polar.

Maneno

1) Eleza jinsi uaminifu unavyoamua sehemu gani ya conic inayotolewa.

Jibu

Ikiwa uaminifu ni chini ya$1$, ni ellipse. Ikiwa eccentricity ni sawa na$1$, ni parabola. Ikiwa uaminifu ni mkubwa kuliko$1$, ni hyperbola.

2) Ikiwa sehemu ya conic imeandikwa kama equation ya polar, ni lazima iwe kweli kwa denominator?

3) Ikiwa sehemu ya conic imeandikwa kama equation ya polar, na denominator inahusisha$\sin \theta$ nini hitimisho linaweza kupatikana kuhusu directrix?

Jibu

Directrix itakuwa sawa na mhimili wa polar.

4) Ikiwa directrix ya sehemu ya conic ni perpendicular kwa mhimili polar, tunajua nini kuhusu equation ya grafu?

5) Tunajua nini kuhusu lengo/foci ya sehemu ya conic ikiwa imeandikwa kama equation polar?

Jibu

Moja ya foci itakuwa iko katika asili.

Kialjebra

Kwa mazoezi 6-17, kutambua conic kwa lengo la asili, na kisha kutoa directrix na eccentricity.

6)$r=\dfrac{6}{1-2\cos \theta }$

7)$r=\dfrac{3}{4-4\sin \theta }$

Jibu

Parabola na$e=1$ na directrix$\dfrac{3}{4}$ vitengo chini pole.

8)$r=\dfrac{8}{4-3\cos \theta }$

9)$r=\dfrac{5}{1+2\sin \theta }$

Jibu

Hyperbola$e=2$ na$\dfrac{5}{2}$ vitengo vya directrix juu ya pole.

10)$r=\dfrac{15}{4+3\cos \theta }$

11)$r=\dfrac{3}{10+10\cos \theta }$

Jibu

Parabola na$e=1$ na directrix$\dfrac{3}{10}$ vitengo na haki ya pole.

12)$r=\dfrac{2}{1-\cos \theta }$

13)$r=\dfrac{4}{7+2\cos \theta }$

Jibu

Ellipse$e=\dfrac{2}{7}$ na$2$ vitengo vya directrix kwa haki ya pole.

14)$r(1-\cos \theta )=3$

15)$r(3+5\sin \theta )=11$

Jibu

Hyperbola$e=\dfrac{5}{3}$ na$\dfrac{11}{5}$ vitengo vya directrix juu ya pole.

16)$r(4-5\sin \theta )=1$

17)$r(7+8\sin \theta )=7$

Jibu

Hyperbola$e=\dfrac{8}{7}$ na$\dfrac{7}{8}$ vitengo vya directrix na haki ya pole.

Kwa mazoezi 18-30, kubadilisha equation ya polar ya sehemu ya conic kwa equation mstatili.

18)$r=\dfrac{4}{1+3\sin \theta }$

19)$r=\dfrac{2}{5-3\sin \theta }$

Jibu

$25x^2+16y^2-12y-4=0$

20)$r=\dfrac{8}{3-2\cos \theta }$

21)$r=\dfrac{3}{2+5\cos \theta }$

Jibu

$21x^2-4y^2-30x+9=0$

22)$r=\dfrac{4}{2+2\sin \theta }$

23)$r=\dfrac{3}{8-8\cos \theta }$

Jibu

$64y^2=48x+9$

24)$r=\dfrac{2}{6+7\cos \theta }$

25)$r=\dfrac{5}{5-11\sin \theta }$

Jibu

$96y^2-25x^2+110y+25=0$

26)$r(5+2\cos \theta )=6$

27)$r(2-\cos \theta )=1$

Jibu

$3x^2+4y^2-2x-1=0$

28)$r(2.5-2.5\sin \theta )=5$

29)$r=\dfrac{6\sec \theta }{-2+3\sec \theta }$

Jibu

$5x^2+9y^2-24x-36=0$

30)$r=\dfrac{6\csc \theta }{3+2\csc \theta }$

Kwa mazoezi 31-42, graph sehemu ya conic iliyotolewa. Ikiwa ni parabola, lebo kipeo, lengo, na directrix. Ikiwa ni ellipse, lebo alama na foci. Ikiwa ni hyperbola, lebo alama na foci.

31)$r=\dfrac{5}{2+\cos \theta }$

Jibu

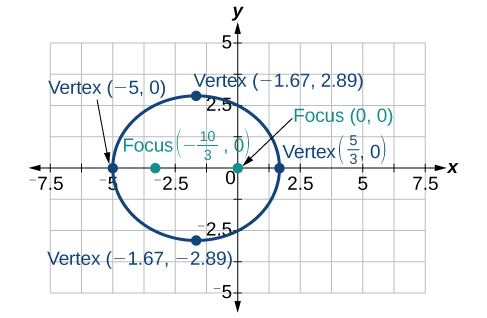
32)$r=\dfrac{2}{3+3\sin \theta }$

33)$r=\dfrac{10}{5-4\sin \theta }$

Jibu

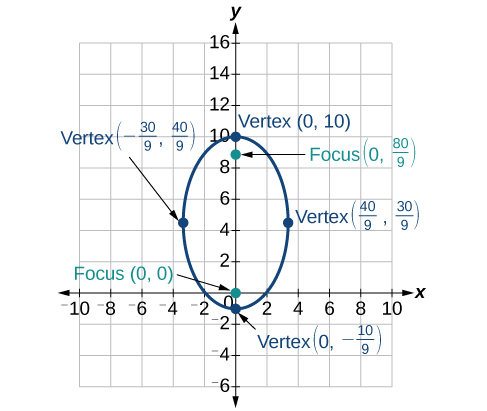
34)$r=\dfrac{3}{1+2\cos \theta }$

35)$r=\dfrac{8}{4-5\cos \theta }$

Jibu

36)$r=\dfrac{3}{4-4\cos \theta }$

37)$r=\dfrac{2}{1-\sin \theta }$

Jibu

38)$r=\dfrac{6}{3+2\sin \theta }$

39)$r(1+\cos \theta )=5$

Jibu

40)$r(3-4\sin \theta )=9$

41)$r(3-2\sin \theta )=6$

Jibu

42)$r(4-6\cos \theta )=5$

Kwa mazoezi 43-, pata equation ya polar ya conic kwa kuzingatia asili na eccentricity iliyotolewa na directrix.

43) Directrix:$x=4$;$e=\dfrac{1}{5}$

Jibu

$r=\dfrac{4}{5+\cos \theta }$

4) Directrix:$x=-4$;$e=5$

45) Directrix:$y=2$;$e=2$

Jibu

$r=\dfrac{4}{1+2\sin \theta }$

46) Directrix:$y=-2$;$e=\dfrac{1}{2}$

47) Directrix:$x=1$;$e=1$

Jibu

$r=\dfrac{1}{1+\cos \theta }$

48) Directrix:$x=-1$;$e=1$

49) Directrix:$x=-\dfrac{1}{4}$;$e=\dfrac{7}{2}$

Jibu

$r=\dfrac{7}{8-28\cos \theta }$

50) Directrix:$y=-\dfrac{2}{5}$;$e=\dfrac{7}{2}$

15) Directrix:$y=4$;$e=\dfrac{3}{2}$

Jibu

$r=\dfrac{12}{2+3\sin \theta }$

52) Directrix:$x=-2$;$e=\dfrac{8}{3}$

53) Directrix:$x=-5$;$e=\dfrac{3}{4}$

Jibu

$r=\dfrac{15}{4-3\cos \theta }$

54) Directrix:$y=2$;$e=2.5$

5) Directrix:$x=-3$;$e=\dfrac{1}{3}$

Jibu

$r=\dfrac{3}{3-3\cos \theta }$

Upanuzi

Kumbuka kutoka kwa Mzunguko wa Axes kwamba usawa wa conics na$xy$ neno umezunguka grafu. Kwa mazoezi yafuatayo, kueleza kila equation katika fomu Polar na$r$ kama kazi ya$\theta$.

56)$xy=2$

57)$x^2+xy+y^2=4$

Jibu

$r=\pm \dfrac{2}{\sqrt{1+\sin \theta \cos \theta }}$

58)$2x^2+4xy+2y^2=9$

59)$16x^2+24xy+9y^2=4$

Jibu

$r=\pm \dfrac{2}{4\cos \theta +3\sin \theta }$

60)$2xy+y=1$

Wachangiaji na Majina

• Template:OpenStaxPreCalc