10.R: Uchambuzi Jiometri (Tathmini)

Last updated
Save as PDF

Page ID: 181545

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

10.1: duaradufu

Katika sehemu hii, sisi kuchunguza sura ya chumba hiki na maombi yake halisi ya dunia, ikiwa ni pamoja na jinsi mbali mbali watu wawili katika Statuary Hall wanaweza kusimama na bado kusikia kila mmoja whisper.

Kwa mazoezi 1-4, andika equation ya ellipse katika fomu ya kawaida. Kisha kutambua kituo, vertices, na foci.

1)$\dfrac{x^2}{25}+\dfrac{y^2}{64}=1$

Jibu: $\dfrac{x^2}{5^2}+\dfrac{y^2}{8^2}=1$; kituo cha:$(0,0)$; Vipeo:$(5,0)$,$(-5,0)$,$(0,8)$,$(0,-8)$; foci:$(0,\sqrt{39})$,$(0,-\sqrt{39})$

2)$\dfrac{(x-2)^2}{100}+\dfrac{(y+3)^2}{36}=1$

3)$9x^2+y^2+54x-4y+76=0$

Jibu: $\dfrac{(x+3)^2}{1^2}+\dfrac{(y-2)^2}{3^2}=1$; kituo cha:$(-3,2)$; Vipeo:$(-2,2)$,$(-4,2)$,$(-3,5)$,$(-3,-1)$; foci:$(-3,2+2\sqrt{2})$,$(-3,2-2\sqrt{2})$

4)$9x^2+36y^2-36x+72y+36=0$

Kwa mazoezi 5-8, grafu ya ellipse, akibainisha kituo, vertices, na foci.

5)$\dfrac{x^2}{36}+\dfrac{y^2}{9}=1$

Jibu

kituo:$(0,0)$; Vipeo:$(6,0$,,$(-6,0)$$(0,3)$,$(0,-3)$; foci:$(3\sqrt{3},0)$,$(-3\sqrt{3},0)$

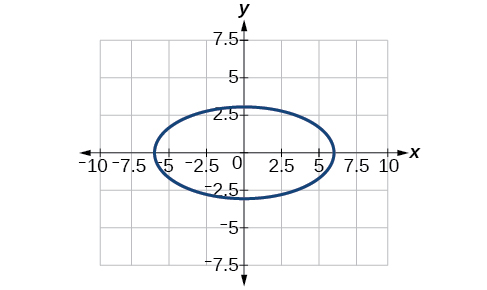
$R10.1.5.png$

6)$\dfrac{(x-4)^2}{25}+\dfrac{(y+3)^2}{49}=1$

7)$4x^2+y^2+16x+4y-44=0$

Jibu

kituo:$(-2,-2)$; Vipeo:$(2,-2)$,,$(-6,-2)$$(-2,6)$,$(-2,-10)$; foci:$(-2,-2+4\sqrt{3})$,$(-2,-2-4\sqrt{3})$

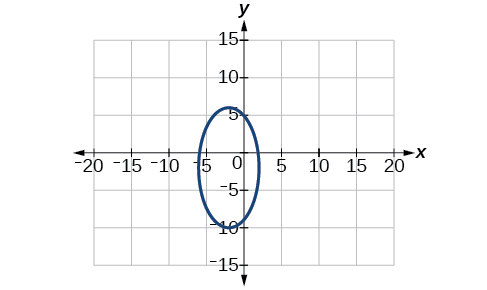
$R10.1.7.png$

8)$2x^2+3y^2-20x+12y+38=0$

Kwa mazoezi 9-11, tumia taarifa iliyotolewa ili kupata equation kwa ellipse.

9) Kituo cha$(0,0)$, kuzingatia$(3,0)$, vertex saa$(-5,0)$

Jibu: $\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$

10) Kituo cha saa$(2,-2)$, vertex saa$(7,-2)$, kuzingatia$(4,-2)$

11) Nyumba ya sanaa ya whispering inapaswa kujengwa kama vile foci iko$35$ miguu kutoka katikati. Ikiwa urefu wa nyumba ya sanaa ni kuwa$100$ miguu, urefu wa dari unapaswa kuwa nini?

Jibu: Takriban$35.71$ miguu

10.2: Hyperbola

Katika jiometri ya uchambuzi, hyperbola ni sehemu ya conic inayoundwa na kuingiliana koni ya mviringo ya mviringo na ndege kwa pembe kama vile nusu zote za koni zimeunganishwa. Mfululizo huu hutoa curves mbili tofauti zisizo na mipaka ambazo ni picha za kioo za kila mmoja.

Kwa mazoezi 1-4, andika equation ya hyperbola katika fomu ya kawaida. Kisha kutoa kituo, vertices, na foci.

1)$\dfrac{x^2}{81}-\dfrac{y^2}{9}=1$

2)$\dfrac{(y+1)^2}{16}-\dfrac{(x-4)^2}{36}=1$

Jibu: $\dfrac{(y+1)^2}{4^2}-\dfrac{(x-4)^2}{6^2}=1$; kituo cha:$(4,-1)$; Vipeo:$(4,3)$,$(4,-5)$; foci:$(4,-1+2\sqrt{13})$,$(4,-1-2\sqrt{13})$

3)$9y^2-4x^2+54y-16x+29=0$

4)$3x^2-y^2-12x-6y-9=0$

Jibu: $\dfrac{(x-2)^2}{2^2}-\dfrac{(y+3)^2}{(2\sqrt{3})^2}=1$; kituo cha:$(2,-3)$; Vipeo:$(4,-3)$,$(0,-3)$; foci:$(6,-3)$,$(-2,-3)$

Kwa mazoezi 5-8, graph hyperbola, alama za kuandika na foci.

5)$\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$

6)$\dfrac{(y-1)^2}{49}-\dfrac{(x+1)^2}{4}=1$

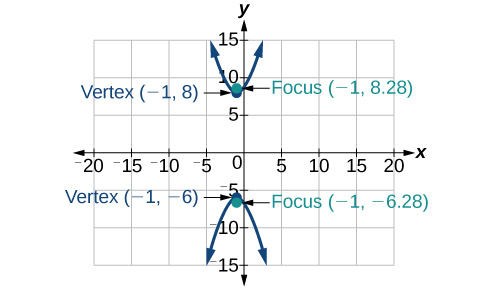
Jibu: $R10.2.6.png$

7)$x^2-4y^2+6x+32y-91=0$

8)$2y^2-x^2-12y-6=0$

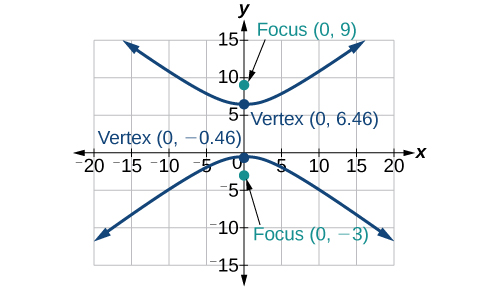
Jibu: $R10.2.8.png$

Kwa mazoezi 9-10, pata equation ya hyperbola.

9) Kituo cha saa$(0,0)$, vertex saa$(0,4)$, kuzingatia$(0,-6)$

10) Foci katika$(3,7)$ na$(7,7)$, vertex saa$(6,7$

Jibu: $\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1$

10.3: Parabola

Kama duaradufu na hyperbola, parabola pia inaweza kuelezwa na seti ya pointi katika ndege ya kuratibu. Parabola ni seti ya pointi zote katika ndege ambayo ni umbali sawa kutoka kwenye mstari uliowekwa, unaoitwa directrix, na hatua ya kudumu (lengo) sio kwenye directrix.

Kwa mazoezi 1-4, andika equation ya parabola katika fomu ya kawaida. Kisha kutoa vertex, lengo, na directrix.

1)$y^2=12x$

2)$(x+2)^2=\dfrac{1}{2}(y-1)$

Jibu: $(x+2)^2=\dfrac{1}{2}(y-1)$; vertex:$(-2,1)$; lengo:$ \left( -2, \dfrac{9}{8} \right ) $; directrix:$y=\dfrac{7}{8}$

3)$y^2-6y-6x-3=0$

4)$x^2+10x-y+23=0$

Jibu: $(x+5)^2=(y+2)$; vertex:$(-5,-2)$; lengo:$ \left( -5, -\dfrac{7}{4} \right ) $; directrix:$y=-\dfrac{9}{4}$

Kwa mazoezi 5-8, graph parabola, lebo vertex, lengo, na directrix.

5)$x^2+4y=0$

6)$(y-1)^2=\dfrac{1}{2}(x+3)$

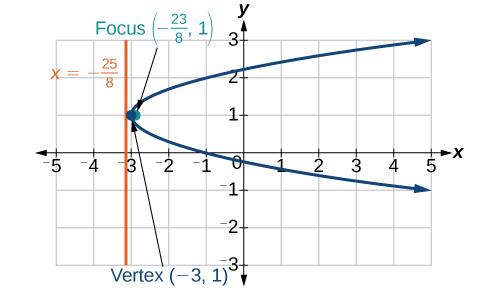
Jibu: $R10.3.6.png$

7)$x^2-8x-10y+46=0$

8)$2y^2+12y+6x+15=0$

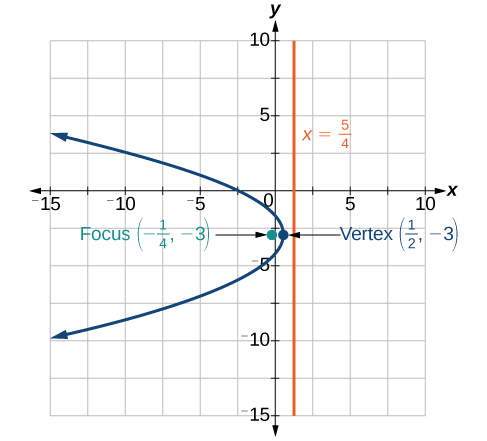
Jibu: $R10.3.8.png$

Kwa mazoezi 9-11, andika equation ya parabola kwa kutumia taarifa iliyotolewa.

9) Kuzingatia$(-4,0)$; directrix ni$x=4$

10) Kuzingatia$ \left( 2, \dfrac{9}{8} \right ) $; directrix ni$y=\dfrac{7}{8}$

Jibu: $(x-2)^2= \left (\dfrac{1}{2} \right ) (y-1)$

11) TV ya cable inayopokea sahani ni sura ya paraboloid ya mapinduzi. Pata eneo la mpokeaji, ambalo linawekwa kwenye lengo, ikiwa sahani ni$5$ miguu kote wakati wa ufunguzi wake na$1.5$ miguu ya kina.

10.4: Mzunguko wa Axes

Katika sehemu zilizopita za sura hii, tuna ililenga equations fomu ya kawaida kwa sehemu nondegenerate conic. Katika sehemu hii, sisi kuhama lengo letu kwa jumla fomu equation, ambayo inaweza kutumika kwa ajili ya conic yoyote. Fomu ya jumla imewekwa sawa na sifuri, na maneno na coefficients hutolewa kwa utaratibu fulani, kama inavyoonyeshwa hapa chini.

Kwa mazoezi 1-3, tambua ni sehemu gani ya conic iliyowakilishwa.

1)$16x^2+24xy+9y^2+24x-60y-60=0$

Jibu: $B^2 - 4AC =0$, parabola

2)$4x^2+14xy+5y^2+18x-6y+30=0$

3)$4x^2+xy+2y^2+8x-26y+9=0$

Jibu: $B^2 - 4AC = -31 < 0$, duaradufu

Kwa mazoezi 4-5, tambua angle$\theta $ ambayo itaondoa$xy$ muda, na uandike usawa unaofanana bila$xy$ muda.

4)$x^2+4xy-2y^2-6=0$

5)$x^2-xy+y^2-6=0$

Jibu: $\theta =45^{\circ},x'^2+3y'^2-12=0$

Kwa mazoezi 6-8, graph equation jamaa na$x'y'$ mfumo ambao equation haina$x'y'$ muda.

6)$9x^2-24xy+16y^2-80x-60y+100=0$

7)$x^2-xy+y^2-2=0$

Jibu

$\theta =45^{\circ}$

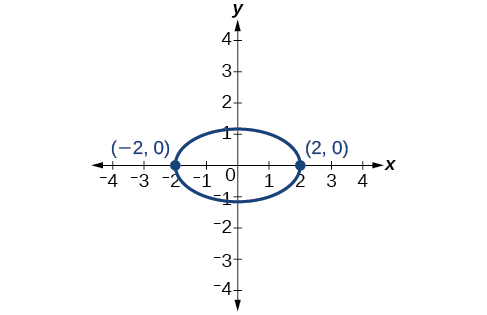
$R10.4.7.png$

8)$6x^2+24xy-y^2-12x+26y+11=0$

10.5: Sehemu za Conic katika Kuratibu za Polar

Katika sehemu hii, tutajifunza jinsi ya kufafanua conic yoyote katika mfumo wa kuratibu wa polar kwa suala la uhakika uliowekwa, lengo la pole, na mstari, directrix, ambayo ni perpendicular kwa mhimili polar.

Kwa mazoezi 1-4, kutokana na equation ya polar ya conic na kuzingatia asili, kutambua eccentricity na directrix.

1)$r=\dfrac{10}{1-5\cos \theta }$

Jibu: Hyperbola$e=5$ na$2$ vitengo vya directrix upande wa kushoto wa pole.

2)$r=\dfrac{6}{3+2\cos \theta }$

3)$r=\dfrac{1}{4+3\sin \theta }$

Jibu: Ellipse$e=\dfrac{3}{4}$ na$\dfrac{1}{3}$ kitengo cha directrix juu ya pole.

4)$r=\dfrac{3}{5-5\sin \theta }$

Kwa mazoezi 5-8, graph conic iliyotolewa katika fomu polar. Ikiwa ni parabola, lebo kipeo, lengo, na directrix. Ikiwa ni ellipse au hyperbola, lebo alama na foci.

5)$r=\dfrac{3}{1-\sin \theta }$

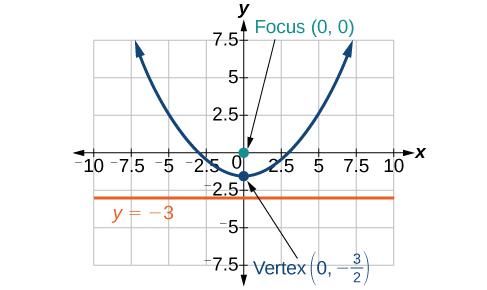
Jibu: $R10.5.5.png$

6)$r=\dfrac{8}{4+3\sin \theta }$

7)$r=\dfrac{10}{4+5\cos \theta }$

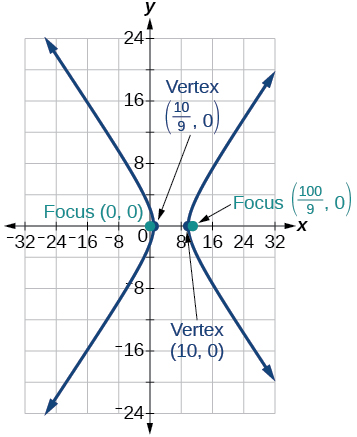
Jibu: $R10.5.7.png$

8)$r=\dfrac{9}{3-6\cos \theta }$

Kwa mazoezi 9-10, kutokana na taarifa kuhusu grafu ya conic na kuzingatia asili, kupata equation katika fomu polar.

9) Directrix ni$x=3$ na uaminifu$e=1$

Jibu: $r=\dfrac{3}{1+\cos \theta }$

10) Directrix ni$y=-2$ na uaminifu$e=4$

Mazoezi mtihani

Kwa mazoezi 1-2, andika equation katika fomu ya kawaida na ueleze kituo, vertices, na foci.

1)$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$

Jibu: $\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1$; katikati:$(0,0)$; vertices:$(3,0)$,$(-3,0)$,$(0,2)$,$(0,-2)$; foci:$(\sqrt{5},0)$,$(-\sqrt{5},0)$

2)$9y^2+16x^2-36y+32x-92=0$

Kwa mazoezi 3-6, mchoro grafu, kutambua kituo, vertices, na foci.

3)$\dfrac{(x-3)^2}{64}+\dfrac{(y-2)^2}{36}=1$

Jibu

kituo:$(3,2)$; vertices:$(11,2)$,$(-5,2)$,$(3,8)$,$(3,-4)$; foci:$(3+2\sqrt{7},2)$,$(3-2\sqrt{7},2)$

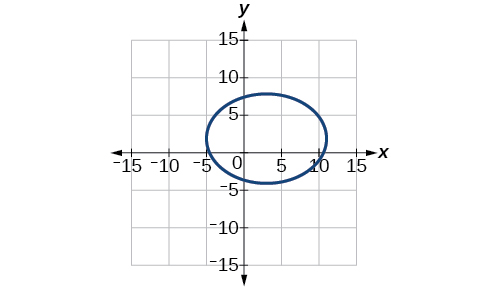
$RP3.png$

4)$2x^2+y^2+8x-6y-7=0$

5) Andika kiwango fomu equation ya duaradufu na kituo cha saa$(1,2)$, vertex katika$(7,2)$, na kuzingatia$(4,2)$.

Jibu: $\dfrac{(x-1)^2}{36}+\dfrac{(y-2)^2}{27}=1$

6) Nyumba ya sanaa ya whispering inapaswa kujengwa kwa urefu wa$150$ miguu. Ikiwa foci zinapaswa kuwa$20$ miguu mbali na ukuta, ni juu gani dari inapaswa kuwa?

Kwa mazoezi 7-8, andika equation ya hyperbola kwa fomu ya kawaida, na kutoa kituo, vertices, foci, na asymptotes.

7)$\dfrac{x^2}{49}-\dfrac{y^2}{81}=1$

Jibu: $\dfrac{x^2}{7^2}-\dfrac{y^2}{9^2}=1$; katikati:$(0,0)$; vertices:$(7,0)$,$(-7,0)$; foci:$(\sqrt{130},0)$,$(-\sqrt{130},0)$; asymptotes:$y=\pm \dfrac{9}{7}x$

8)$16y^2-9x^2+128y+112=0$

Kwa mazoezi 9-11, graph hyperbola, akibainisha kituo chake, vertices, na foci. Weka usawa wa asymptotes.

9)$\dfrac{(x-3)^2}{25}-\dfrac{(y+3)^2}{1}=1$

Jibu

kituo:$(3,-3)$; vertices:$(8,-3)$,$(-2,-3)$; foci:$(3+\sqrt{26},-3)$,$(3-\sqrt{26},-3)$; asymptotes:$y=\pm \dfrac{1}{5}(x-3)-3$

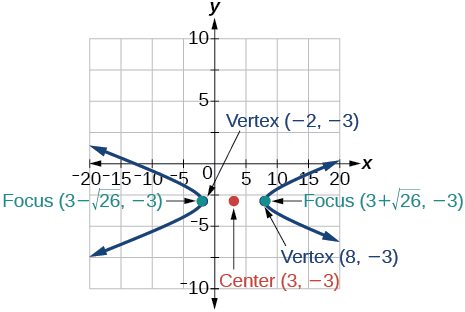
$RP9.png$

10)$y^2-x^2+4y-4x-18=0$

11) Andika usawa wa fomu ya kawaida ya hyperbola na foci katika$(1,0)$$(1,6)$, na, na vertex saa$(1,2)$.

Jibu: $\dfrac{(y-3)^2}{1}-\dfrac{(x-1)^2}{8}=1$

Kwa mazoezi 12-13, andika equation ya parabola katika fomu ya kawaida, na kutoa vertex, lengo, na equation ya directrix.

12)$y^2+10x=0$

13)$3x^2-12x-y+11=0$

Jibu: $(x-2)^2=\dfrac{1}{3}(y+1)$; vertex:$(2,-1)$; lengo:$(2,-\dfrac{11}{12})$; directrix:$y=-\dfrac{13}{12}$

Kwa mazoezi 14-17, graph parabola, kuandika vertex, lengo, na directrix.

14)$(x-1)^2=-4(y+3)$

15)$y^2+8x-8y+40=0$

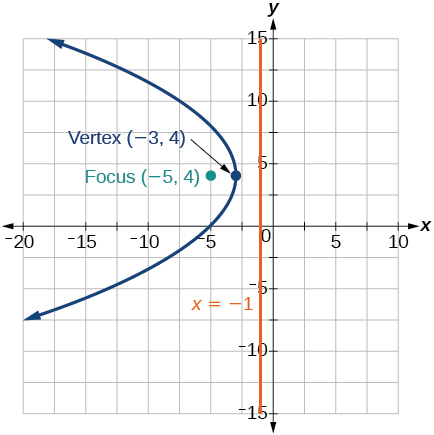
Jibu: $RP15.png$

16) Andika equation ya parabola kwa lengo$(2,3)$ na directrix$y=-1$.

17) Mwangaza wa utafutaji umeumbwa kama paraboloidi ya mapinduzi. Ikiwa chanzo cha mwanga iko$1.5$ miguu kutoka msingi pamoja na mhimili wa ulinganifu, na kina cha utafutaji ni$3$ miguu, upana wa ufunguzi unapaswa kuwa nini?

Jibu: Takriban$8.49$ miguu

Kwa mazoezi 18-19, tambua sehemu gani ya conic inawakilishwa na equation iliyotolewa, na kisha uamua angle$\theta$ ambayo itaondoa$xy$ muda.

18)$3x^2-2xy+3y^2=4$

19)$x^2+4xy+4y^2+6x-8y=0$

Jibu: parabola;$\theta \approx 63.4^{\circ}$

Kwa mazoezi 20-21, andika tena katika$x'y'$ mfumo bila$x'y'$ muda, na graph grafu iliyozungushwa.

20)$11x^2+10\sqrt{3}xy+y^2=4$

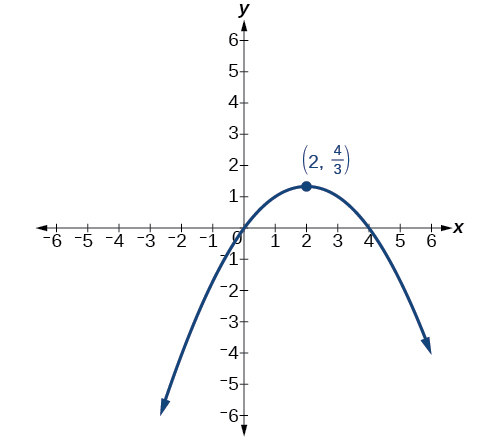
21)$16x^2+24xy+9y^2-125x=0$

Jibu

$x'^2-4x'+3y'=0$

$RP21.png$

Kwa mazoezi 22-23, kutambua conic kwa kuzingatia asili, na kisha kutoa directrix na eccentricity.

22)$r=\dfrac{3}{2-\sin \theta }$

23)$r=\dfrac{5}{4+6\cos \theta }$

Jibu: Hyperbola$e=\dfrac{3}{2}$ na$\dfrac{5}{6}$ vitengo vya directrix na haki ya pole.

Kwa mazoezi 24-26, graph sehemu ya conic iliyotolewa. Kama ni parabola, studio vertex, lengo, na directrix. Ikiwa ni ellipse au hyperbola, alama za studio na foci.

24)$r=\dfrac{12}{4-8\sin \theta }$

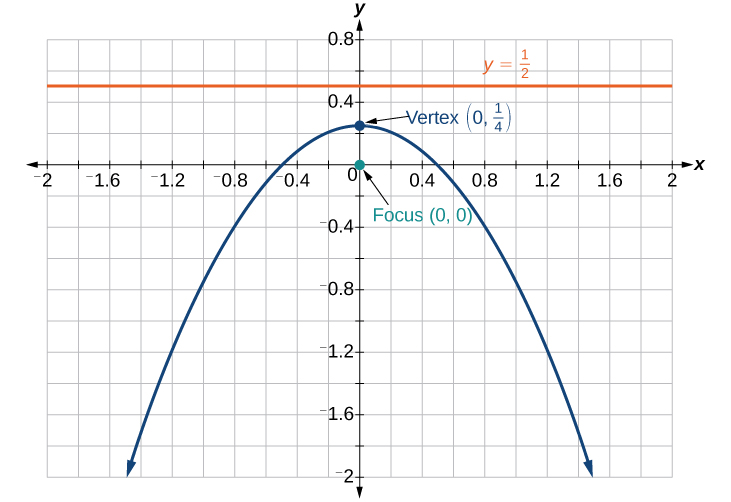
25)$r=\dfrac{2}{4+4\sin \theta }$

Jibu: $RP25.png$

26) Kupata equation polar ya conic na lengo katika asili, eccentricity ya$e=2$, na directrix:$x=3$.

Wachangiaji na Majina

Template:OpenStaxPreCalc