10.5: Sehemu za Conic katika Kuratibu za Polar
- Page ID
- 181518
- Tambua conic katika fomu ya polar.
- Graph equations polar ya conics.
- Kufafanua conics katika suala la lengo na directrix.
Wengi wetu tunajua mwendo wa orbital, kama mwendo wa sayari inayozunguka jua au elektroni inayozunguka kiini atomia. Ndani ya mfumo wa sayari, njia za sayari, asteroids, na comets karibu na mwili mkubwa wa mbinguni mara nyingi ni elliptical. Comets, hata hivyo, inaweza kuchukua obiti parabolic au hyperbolic badala. Na, kwa kweli, sifa za njia za sayari zinaweza kutofautiana kwa muda. Kila obiti imefungwa kwa eneo la mwili wa mbinguni unaozunguka na umbali na mwelekeo wa sayari au kitu kingine kutoka kwa mwili huo. Matokeo yake, tunatumia kutumia viwianishi vya polar ili kuwakilisha njia hizi.
Katika obiti ya elliptical, periapsis ni hatua ambayo vitu viwili viko karibu, na apoapsis ni hatua ambayo wao ni mbali zaidi. Kwa ujumla, kasi ya mwili unaozunguka huelekea kuongezeka huku inakaribia periapsis na kupungua kadiri inakaribia apoapsis. Vitu vingine hufikia kasi ya kutoroka, ambayo husababisha obiti isiyo na kipimo. Miili hii inaonyesha ama parabolic au obiti ya hyperbolic kuhusu mwili; mwili unaozunguka huvunja bila kuvuta mvuto wa mwili wa mbinguni na kuwaka ndani ya angani. Kila moja ya njia hizi zinaweza kutajwa na sehemu ya conic katika mfumo wa kuratibu polar.
Kutambua Conic katika Fomu ya Polar
Conic yoyote inaweza kuamua na sifa tatu: lengo moja, mstari uliowekwa unaoitwa directrix, na uwiano wa umbali wa kila mmoja hadi hatua kwenye grafu. Fikiria parabola\(x=2+y^2\) inavyoonekana katika Kielelezo\(\PageIndex{2}\).
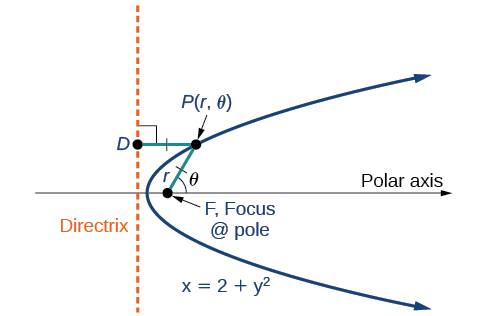
Tulijifunza hapo awali jinsi parabola inavyoelezwa na lengo (hatua ya kudumu) na directrix (mstari uliowekwa). Katika sehemu hii, tutajifunza jinsi ya kufafanua conic yoyote katika mfumo wa kuratibu wa polar kwa suala la uhakika uliowekwa,\(P(r,\theta)\) lengo la pole, na mstari, directrix, ambayo ni perpendicular kwa mhimili polar.
Kama\(F\) ni hatua fasta, lengo, na\(D\) ni fasta line, directrix, basi tunaweza basi\(e\) kuwa fasta chanya idadi, aitwaye eccentricity, ambayo tunaweza kufafanua kama uwiano wa umbali kutoka hatua kwenye grafu kwa lengo na uhakika juu ya grafu kwa directrix. Kisha seti ya pointi zote\(P\) kama hiyo\(e=\dfrac{PF}{PD}\) ni conic. Kwa maneno mengine, tunaweza kufafanua conic kama seti ya pointi zote\(P\) na mali ambayo uwiano wa umbali kutoka\(P\)\(F\) hadi umbali kutoka\(P\) kwa\(D\) ni sawa na mara kwa mara\(e\).
Kwa conic na eccentricity\(e\),
- ikiwa\(0≤e<1\), conic ni duaradufu
- ikiwa\(e=1\), conic ni parabola
- ikiwa\(e>1\), conic ni hyperbola
Kwa ufafanuzi huu, tunaweza sasa kufafanua conic kwa suala la directrix\(x=\pm p\), eccentricity\(e\), na angle\(\theta\). Hivyo, kila conic inaweza kuandikwa kama equation polar, equation iliyoandikwa katika suala la\(r\) na\(\theta\).
Kwa conic yenye lengo la asili, ikiwa directrix ni\(x=\pm p\), wapi\(p\) idadi halisi ya chanya, na eccentricity ni idadi halisi nzuri\(e\), conic ina equation polar
\[r=\dfrac{ep}{1\pm e \cos \theta}\]
Kwa conic yenye lengo la asili, ikiwa directrix ni\(y=\pm p\), wapi\(p\) idadi halisi ya chanya, na eccentricity ni idadi halisi nzuri\(e\), conic ina equation polar
\[r=\dfrac{ep}{1\pm e \sin \theta}\]
- Kuzidisha nambari na denominator kwa usawa wa mara kwa mara katika denominator ili kuandika upya equation katika fomu ya kawaida.
- Kutambua eccentricity\(e\) kama mgawo wa kazi trigonometric katika denominator.
- \(e\)Linganisha na\(1\) kuamua sura ya conic.
- Kuamua directrix\(x=p\) kama cosine iko katika denominator na\(y=p\) kama sine iko katika denominator. Weka\(ep\) sawa na nambari katika fomu ya kawaida ili kutatua\(x\) au\(y\).
Kwa kila moja ya equations zifuatazo, tambua conic kwa kuzingatia asili, directrix, na eccentricity.
- \(r=\dfrac{6}{3+2 \sin \theta}\)
- \(r=\dfrac{12}{4+5 \cos \theta}\)
- \(r=\dfrac{7}{2−2 \sin \theta}\)
Suluhisho
Kwa kila moja ya conics tatu, tutaandika upya equation katika fomu ya kawaida. Standard aina ina\(1\) kama mara kwa mara katika denominator. Kwa hiyo, katika sehemu zote tatu, hatua ya kwanza itakuwa kuzidisha nambari na denominator kwa usawa wa mara kwa mara ya equation ya awali\(\dfrac{1}{c}\), ambapo\(c\) ni mara kwa mara.
- Panua nambari na denominator na\(\dfrac{1}{3}\).
\(r=\dfrac{6}{3+2\sin \theta}⋅\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{1}{3}\right)}=\dfrac{6\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+2\left(\dfrac{1}{3}\right)\sin \theta}=\dfrac{2}{1+\dfrac{2}{3} \sin \theta}\)
Kwa sababu\(\sin \theta\) ni katika denominator, directrix ni\(y=p\). Kulinganisha na fomu ya kawaida, kumbuka\(e=\dfrac{2}{3}\) kwamba.Kwa hiyo, kutoka kwa namba,
\[\begin{align*} 2&=ep\\ 2&=\dfrac{2}{3}p\\ \left(\dfrac{3}{2}\right)2&=\left(\dfrac{3}{2}\right)\dfrac{2}{3}p\\ 3&=p \end{align*}\]
Tangu\(e<1\), conic ni ellipse. Eccentricity ni\(e=\dfrac{2}{3}\) na directrix ni\(y=3\).
- Panua nambari na denominator na\(\dfrac{1}{4}\).
\[\begin{align*} r&=\dfrac{12}{4+5 \cos \theta}\cdot \dfrac{\left(\dfrac{1}{4}\right)}{\left(\dfrac{1}{4}\right)}\\ r&=\dfrac{12\left(\dfrac{1}{4}\right)}{4\left(\dfrac{1}{4}\right)+5\left(\dfrac{1}{4}\right)\cos \theta}\\ r&=\dfrac{3}{1+\dfrac{5}{4} \cos \theta} \end{align*}\]
Kwa sababu\(\cos \theta\) ni katika denominator, directrix ni\(x=p\). Kulinganisha na fomu ya kawaida,\(e=\dfrac{5}{4}\). Kwa hiyo, kutoka kwa nambari,
\[\begin{align*} 3&=ep\\ 3&=\dfrac{5}{4}p\\ \left(\dfrac{4}{5}\right)3&=\left(\dfrac{4}{5}\right)\dfrac{5}{4}p\\ \dfrac{12}{5}&=p \end{align*}\]
Tangu\(e>1\), conic ni hyperbola. Eccentricity ni\(e=\dfrac{5}{4}\) na directrix ni\(x=\dfrac{12}{5}=2.4\).
- Panua nambari na denominator na\(\dfrac{1}{2}\).
\[\begin{align*} r&=\dfrac{7}{2-2 \sin \theta}\cdot \dfrac{\left(\dfrac{1}{2}\right)}{\left(\dfrac{1}{2}\right)}\\ r&=\dfrac{7\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)-2\left(\dfrac{1}{2}\right) \sin \theta}\\ r&=\dfrac{\dfrac{7}{2}}{1-\sin \theta} \end{align*}\]
Kwa sababu sine iko katika denominator, directrix ni\(y=−p\). Kulinganisha na fomu ya kawaida,\(e=1\). Kwa hiyo, kutoka kwa nambari,
\[\begin{align*} \dfrac{7}{2}&=ep\\ \dfrac{7}{2}&=(1)p\\ \dfrac{7}{2}&=p \end{align*}\]
Kwa sababu\(e=1\), conic ni parabola. Eccentricity ni\(e=1\) na directrix ni\(y=−\dfrac{7}{2}=−3.5\).
Tambua conic kwa kuzingatia asili, directrix, na eccentricity kwa\(r=\dfrac{2}{3−\cos \theta}\).
- Jibu
-
duaradufu\(e=\dfrac{1}{3}\);\(x=−2\)
Kuchora Ulinganisho wa Polar wa Conics
Wakati wa kuchora katika kuratibu za Cartesian, kila sehemu ya conic ina equation ya kipekee. Hii sio wakati unapopiga picha katika kuratibu za polar. Tunapaswa kutumia uaminifu wa sehemu ya conic ili kuamua aina gani ya safu ya grafu, na kisha ueleze sifa zake maalum. Hatua ya kwanza ni kuandika upya conic katika fomu ya kawaida kama tulivyofanya katika mfano uliopita. Kwa maneno mengine, tunahitaji kuandika upya equation ili denominator itaanza na\(1\). Hii inatuwezesha kuamua\(e\) na, kwa hiyo, sura ya curve. Hatua inayofuata ni kubadilisha maadili\(\theta\) na kutatua kwa\(r\) kupanga njama chache muhimu. Kuweka\(\theta\) sawa na\(0\)\(\dfrac{\pi}{2}\),\(\pi\),, na\(\dfrac{3\pi}{2}\) hutoa vipeo ili tuweze kuunda mchoro mbaya wa grafu.
Grafu\(r=\dfrac{5}{3+3 \cos \theta}\).
Suluhisho
Kwanza, tunaandika tena conic kwa fomu ya kawaida kwa kuzidisha nambari na denominator kwa usawa wa\(3\), ambayo ni\(\dfrac{1}{3}\).
\[\begin{align*} r &= \dfrac{5}{3+3 \cos \theta}=\dfrac{5\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+3\left(\dfrac{1}{3}\right)\cos \theta} \\ r &= \dfrac{\dfrac{5}{3}}{1+\cos \theta} \end{align*}\]
Kwa sababu\(e=1\), tutaweka graph parabola kwa lengo la asili. kazi ina\(\cos \theta\), na kuna ishara ya kuongeza katika denominator, hivyo directrix ni\(x=p\).
\[\begin{align*} \dfrac{5}{3}&=ep\\ \dfrac{5}{3}&=(1)p\\ \dfrac{5}{3}&=p \end{align*}\]
Directrix ni\(x=\dfrac{5}{3}\).
Kupanga pointi chache muhimu kama katika Jedwali\(\PageIndex{1}\) itatuwezesha kuona vipeo. Angalia Kielelezo\(\PageIndex{3}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{5}{3+3 \cos \theta}\) | \(\dfrac{5}{6}≈0.83\) | \(\dfrac{5}{3}≈1.67\) | haijafafanuliwa | \(\dfrac{5}{3}≈1.67\) |
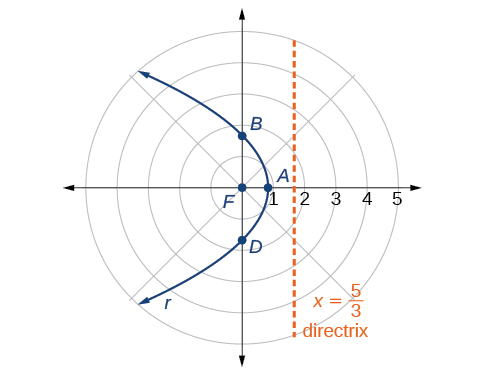
Tunaweza kuangalia matokeo yetu kwa matumizi ya graphing. Angalia Kielelezo\(\PageIndex{4}\).
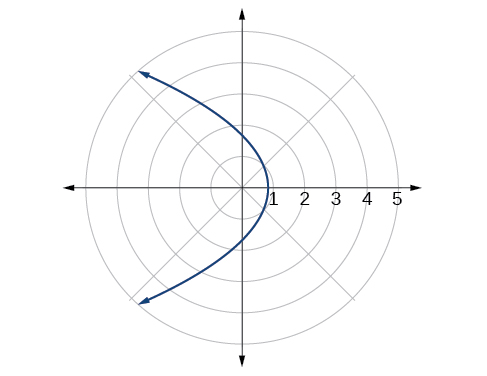
Grafu\(r=\dfrac{8}{2−3 \sin \theta}\).
Suluhisho
Kwanza, tunaandika tena conic kwa fomu ya kawaida kwa kuzidisha nambari na denominator kwa usawa wa\(2\), ambayo ni\(\dfrac{1}{2}\).
\[\begin{align*} r &=\dfrac{8}{2−3\sin \theta}=\dfrac{8\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)−3\left(\dfrac{1}{2}\right)\sin \theta} \\ r &= \dfrac{4}{1−\dfrac{3}{2} \sin \theta} \end{align*}\]
Kwa sababu\(e=\dfrac{3}{2}\)\(e>1\), kwa hiyo tutaweka graph hyperbola kwa lengo la asili. Kazi ina\(\sin \theta\) muda na kuna ishara ya kuondoa katika denominator, hivyo directrix ni\(y=−p\).
\[\begin{align*} 4&=ep\\ 4&=\left(\dfrac{3}{2}\right)p\\ 4\left(\dfrac{2}{3}\right)&=p\\ \dfrac{8}{3}&=p \end{align*}\]
Directrix ni\(y=−\dfrac{8}{3}\).
Kupanga pointi chache muhimu kama katika Jedwali\(\PageIndex{2}\) itatuwezesha kuona vipeo. Angalia Kielelezo\(\PageIndex{5}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{8}{2−3\sin \theta}\) | \(4\) | \(−8\) | \(4\) | \(\dfrac{8}{5}=1.6\) |
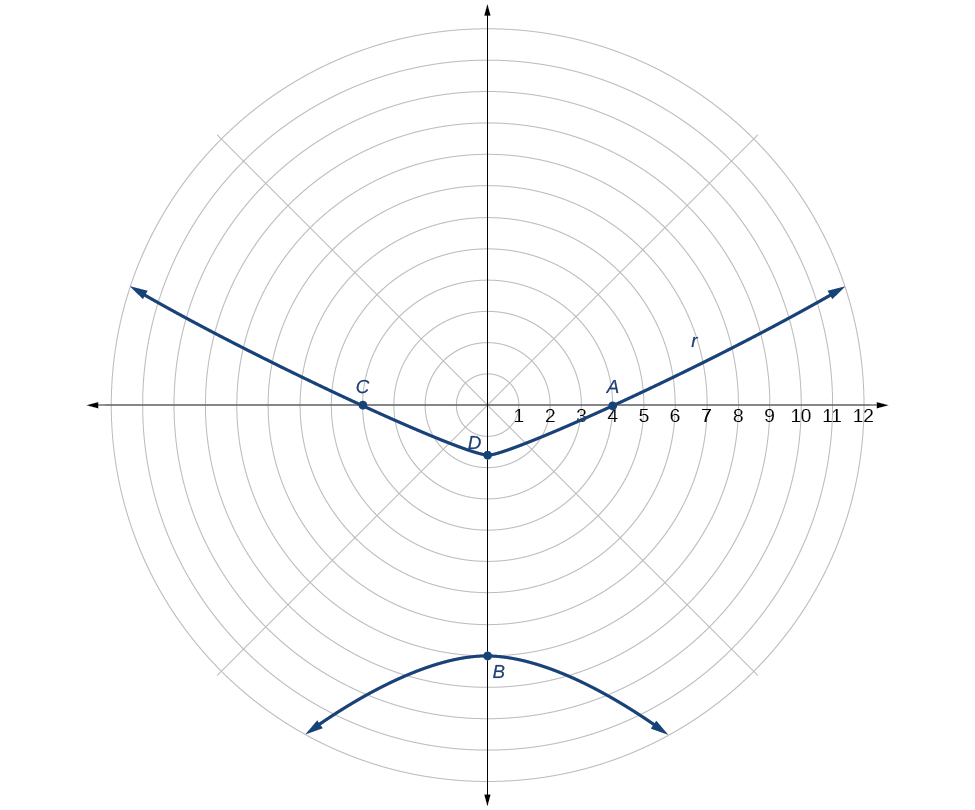
Grafu\(r=\dfrac{10}{5−4 \cos \theta}\).
Suluhisho
Kwanza, tunaandika tena conic kwa fomu ya kawaida kwa kuzidisha nambari na denominator kwa usawa wa 5, yaani\(\dfrac{1}{5}\).
\[\begin{align*} r &= \dfrac{10}{5−4\cos \theta}=\dfrac{10\left(\dfrac{1}{5}\right)}{5\left(\dfrac{1}{5}\right)−4\left(\dfrac{1}{5}\right)\cos \theta} \\ r &= \dfrac{2}{1−\dfrac{4}{5} \cos \theta} \end{align*}\]
Kwa sababu\(e=\dfrac{4}{5}\)\(e<1\), kwa hiyo tutaweka grafu ya ellipse kwa lengo la asili. Kazi ina\(\cos \theta\), na kuna ishara ya kuondoa katika denominator, hivyo directrix ni\(x=−p\).
\[\begin{align*} 2&=ep\\ 2&=\left(\dfrac{4}{5}\right)p\\ 2\left(\dfrac{5}{4}\right)&=p\\ \dfrac{5}{2}&=p \end{align*}\]
Directrix ni\(x=−\dfrac{5}{2}\).
Kupanga pointi chache muhimu kama katika Jedwali\(\PageIndex{3}\) itatuwezesha kuona vipeo. Angalia Kielelezo\(\PageIndex{6}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{10}{5−4 \cos \theta}\) | \(10\) | \(2\) | \(\dfrac{10}{9}≈1.1\) | \(2\) |
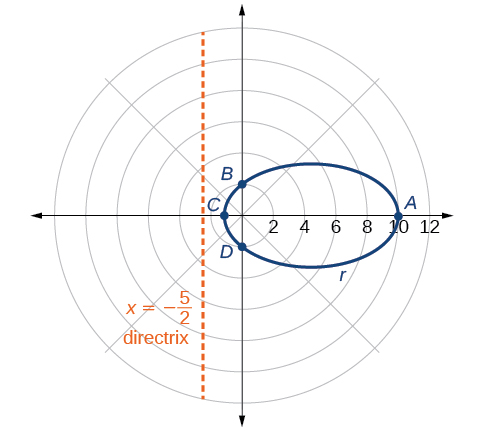
Uchambuzi
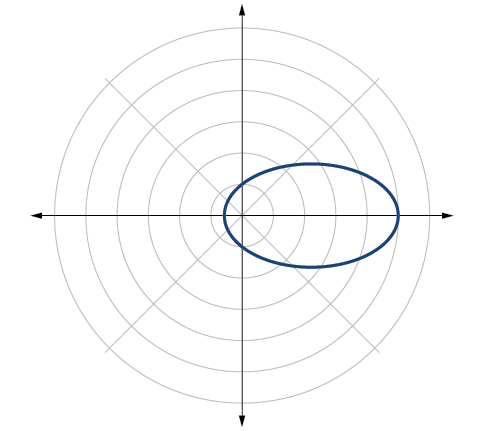
Tunaweza kuangalia matokeo yetu kwa kutumia matumizi ya graphing. Angalia Kielelezo\(\PageIndex{7}\).
Grafu\(r=\dfrac{2}{4−\cos \theta}\).
- Jibu
-
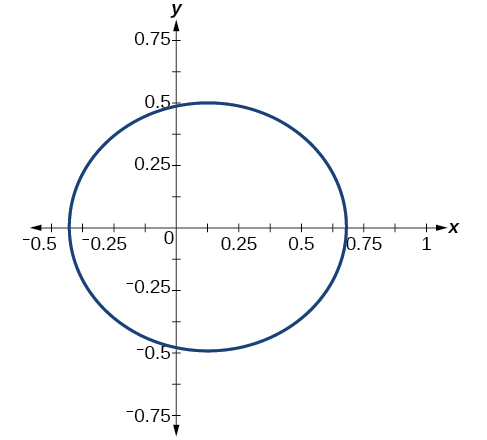
Kielelezo\(\PageIndex{7}\)
Kufafanua Conics katika Masharti ya Mtazamo na Directrix
Hadi sasa tumekuwa kutumia milinganyo Polar ya conics kuelezea na graph Curve. Sasa tutafanya kazi kinyume; tutatumia habari kuhusu asili, eccentricity, na directrix kuamua equation polar.
- Kuamua kama directrix ni usawa au wima. Ikiwa directrix inapewa kwa suala la\(y\), tunatumia fomu ya polar ya jumla kwa suala la sine. Ikiwa directrix inapewa kwa suala la\(x\), tunatumia fomu ya polar ya jumla kwa suala la cosine.
- Tambua ishara katika denominator. Ikiwa\(p<0\), tumia uondoaji. Ikiwa\(p>0\), tumia kuongeza.
- Andika mgawo wa kazi ya trigonometric kama eccentricity iliyotolewa.
- Andika thamani kamili ya\(p\) katika nambari, na uwezesha usawa.
Kupata aina polar ya conic kupewa lengo katika asili,\(e=3\) na directrix\(y=−2\).
Suluhisho
directrix ni\(y=−p\), hivyo tunajua kazi trigonometric katika denominator ni sine.
Kwa sababu\(y=−2\)\(–2<0\), kwa hiyo tunajua kuna ishara ya kuondoa katika denominator. Tunatumia fomu ya kiwango cha
\(r=\dfrac{ep}{1−e \sin \theta}\)
\(e=3\)na\(|−2|=2=p\).
Kwa hiyo,
\[\begin{align*} r&=\dfrac{(3)(2)}{1-3 \sin \theta}\\ r&=\dfrac{6}{1-3 \sin \theta} \end{align*}\]
Kupata aina polar ya conic kupewa lengo katika asili,\(e=\dfrac{3}{5}\), na directrix\(x=4\).
Suluhisho
Kwa sababu directrix ni\(x=p\), tunajua kazi katika denominator ni cosine. Kwa sababu\(x=4\)\(4>0\),, hivyo tunajua kuna ishara ya kuongeza katika denominator. Tunatumia fomu ya kiwango cha
\(r=\dfrac{ep}{1+e \cos \theta}\)
\(e=\dfrac{3}{5}\)na\(|4|=4=p\).
Kwa hiyo,
\[\begin{align*} r &= \dfrac{\left(\dfrac{3}{5}\right)(4)}{1+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{\dfrac{12}{5}}{1+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{1\left(\dfrac{5}{5}\right)+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{\dfrac{5}{5}+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{12}{5}⋅\dfrac{5}{5+3\cos\theta} \\ r &=\dfrac{12}{5+3\cos\theta} \end{align*}\]
Kupata aina polar ya conic kupewa lengo katika asili,\(e=1\), na directrix\(x=−1\).
- Jibu
-
\(r=\dfrac{1}{1−\cos\theta}\)
Badilisha conic\(r=\dfrac{1}{5−5\sin \theta}\) kwa fomu ya mstatili.
Suluhisho
Sisi upya formula kutumia utambulisho\(r=\sqrt{x^2+y^2}\),\(x=r \cos \theta\), na\(y=r \sin \theta\).
\[\begin{align*} r&=\dfrac{1}{5-5 \sin \theta} \\ r\cdot (5-5 \sin \theta)&=\dfrac{1}{5-5 \sin \theta}\cdot (5-5 \sin \theta)\qquad \text{Eliminate the fraction.} \\ 5r-5r \sin \theta&=1 \qquad \text{Distribute.} \\ 5r&=1+5r \sin \theta \qquad \text{Isolate }5r. \\ 25r^2&={(1+5r \sin \theta)}^2 \qquad \text{Square both sides. } \\ 25(x^2+y^2)&={(1+5y)}^2 \qquad \text{Substitute } r=\sqrt{x^2+y^2} \text{ and }y=r \sin \theta. \\ 25x^2+25y^2&=1+10y+25y^2 \qquad \text{Distribute and use FOIL. } \\ 25x^2-10y&=1 \qquad \text{Rearrange terms and set equal to 1.} \end{align*}\]
Badilisha conic\(r=\dfrac{2}{1+2 \cos \theta}\) kwa fomu ya mstatili.
- Jibu
-
\(4−8x+3x^2−y^2=0\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na conics katika kuratibu za polar.
- Ulinganisho wa Polar wa Sehemu za Conic
- Kuchora Ulinganisho wa Polar wa Conics - 1
- Kuchora Ulinganisho wa Polar wa Conics - 2
Ziara tovuti hii kwa maswali ya ziada mazoezi kutoka Learningpod.
Dhana muhimu
- Conic yoyote inaweza kuamua na lengo moja, eccentricity sambamba, na directrix. Tunaweza pia kufafanua conic kwa suala la hatua ya kudumu,\(P(r,\theta)\) lengo la pole, na mstari, directrix, ambayo ni perpendicular kwa mhimili polar.
- Conic ni seti ya pointi zote\(e=\dfrac{PF}{PD}\), ambapo eccentricity\(e\) ni idadi halisi ya chanya. Kila conic inaweza kuandikwa kwa suala la usawa wake wa polar. Angalia Mfano\(\PageIndex{1}\).
- Equations polar ya conics inaweza kuwa graphed. Angalia Mfano\(\PageIndex{2}\), Mfano\(\PageIndex{3}\), na Mfano\(\PageIndex{4}\).
- Conics inaweza kuelezwa katika suala la lengo, directrix, na eccentricity. Angalia Mfano\(\PageIndex{5}\) na Mfano\(\PageIndex{6}\).
- Tunaweza kutumia utambulisho\(r=\sqrt{x^2+y^2}\),\(x=r \cos \theta\), na\(y=r \sin \theta\) kubadili equation kwa conic kutoka polar kwa mstatili fomu. Angalia Mfano\(\PageIndex{7}\).


