10.4: Mzunguko wa Axes

Last updated
Save as PDF

Page ID: 181531

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kutambua sehemu nondegenerate conic kutokana na equations yao ya jumla fomu.
Tumia mzunguko wa axes formula.
Andika equations ya conics kuzungushwa katika fomu ya kawaida.
Tambua conics bila axes zinazozunguka.

Kama tulivyoona, sehemu conic ni sumu wakati ndege intersects mbili kulia mviringo mbegu iliyokaa ncha kwa ncha na kupanua kubwa mbali katika pande kinyume, ambayo sisi pia wito koni. Njia ambayo sisi hupiga koni itaamua aina ya sehemu ya conic iliyoundwa katika makutano. Mduara hutengenezwa kwa kupiga koni na ndege perpendicular kwa mhimili wa ulinganifu wa koni. Ellipse hutengenezwa kwa kupiga koni moja na ndege iliyopandwa sio perpendicular kwa mhimili wa ulinganifu. Parabola hutengenezwa kwa kupiga ndege kwa njia ya juu au chini ya koni mbili, wakati hyperbola hutengenezwa wakati ndege inapiga vipande juu na chini ya koni (Kielelezo$\PageIndex{1}$).

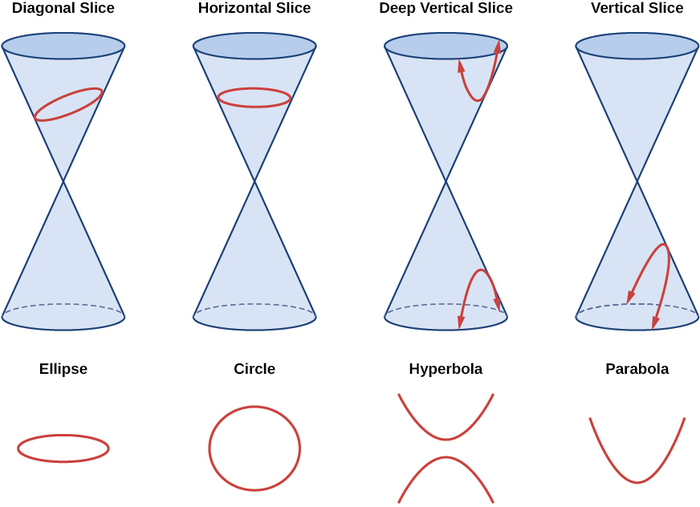
$imageedit_2_4675119068.jpg$

Kielelezo$\PageIndex{1}$: sehemu nondegenerate conic

Ellipses, miduara, hyperbolas, na parabolas wakati mwingine huitwa sehemu za conic zisizo na degenerate, kinyume na sehemu za conic zilizoharibika, ambazo zinaonyeshwa kwenye Mchoro$\PageIndex{2}$. matokeo degenerate conic wakati ndege intersects koni mara mbili na hupita kupitia kilele. Kulingana na angle ya ndege, aina tatu za sehemu za conic zilizoharibika zinawezekana: hatua, mstari, au mistari miwili ya kuingiliana.

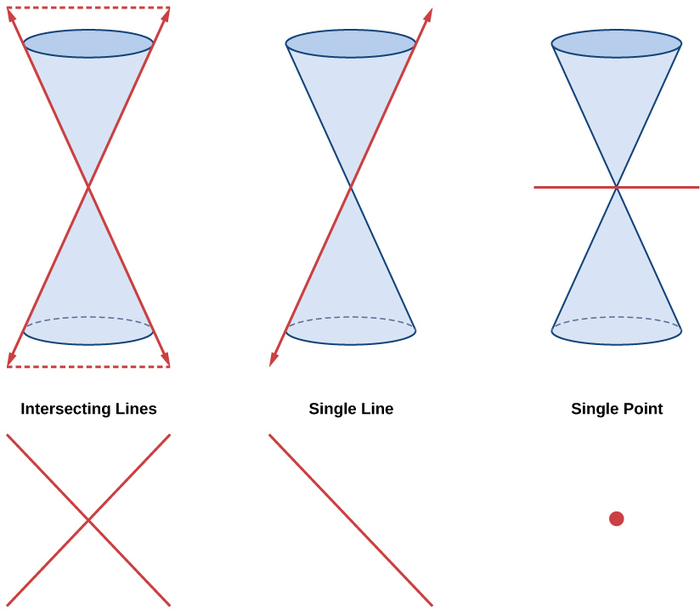
$imageedit_6_5854995623.jpg$

Kielelezo$\PageIndex{2}$: Sehemu za conic zilizoharibika

Kutambua Conics Nondegenerate katika Fomu ya jumla

Katika sehemu zilizopita za sura hii, tuna ililenga equations fomu ya kawaida kwa sehemu nondegenerate conic. Katika sehemu hii, sisi kuhama lengo letu kwa jumla fomu equation, ambayo inaweza kutumika kwa ajili ya conic yoyote. Fomu ya jumla imewekwa sawa na sifuri, na maneno na coefficients hutolewa kwa utaratibu fulani, kama inavyoonyeshwa hapa chini.

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

ambapo$A$,$B$, na$C$ si wote sifuri. Tunaweza kutumia maadili ya coefficients kutambua aina gani conic inawakilishwa na equation iliyotolewa.

Unaweza kugundua kwamba jumla fomu equation ina$xy$ neno kwamba sisi si kuona katika yoyote ya equations kiwango fomu. Kama tutakavyojadili baadaye,$xy$ neno huzunguka conic wakati wowote$B$ si sawa na sifuri.

**Jedwali$\PageIndex{1}$**
Sehemu za Conic	Mfano
duaradufu	$4x^2+9y^2=1$
mduara	$4x^2+4y^2=1$
hyperbola	$4x^2−9y^2=1$
parabola	$4x^2=9y$au$4y^2=9x$
mstari mmoja	$4x+9y=1$
mistari ya kuingiliana	$(x−4)(y+4)=0$
mistari sambamba	$(x−4)(x−9)=0$
uhakika	$4x^2+4y^2=0$
hakuna grafu	$4x^2+4y^2=−1$

AINA YA JUMLA YA SEHEMU ZA CONIC

Sehemu ya conic ina fomu ya jumla

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \label{gen}\]

ambapo$A$,$B$, na$C$ si wote sifuri. Jedwali$\PageIndex{2}$ muhtasari sehemu tofauti conic ambapo$B=0$,$A$ na$C$ ni nonzero namba halisi. Hii inaonyesha kwamba conic haijawahi kuzungushwa.

**Jedwali$\PageIndex{2}$**
duaradufu	$Ax^2+Cy^2+Dx+Ey+F=0$,$A≠C$ na$AC>0$
mduara	$Ax^2+Cy^2+Dx+Ey+F=0$,$A=C$
hyperbola	$Ax^2−Cy^2+Dx+Ey+F=0$au$−Ax^2+Cy^2+Dx+Ey+F=0$, wapi$A$ na$C$ ni chanya
parabola	$Ax^2+Dx+Ey+F=0$au$Cy^2+Dx+Ey+F=0$

Jinsi ya: Kutokana na equation ya conic, kutambua aina ya conic

Andika upya equation kwa fomu ya jumla (Equation\ ref {gen}),$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$
Tambua maadili ya$A$ na$C$ kutoka kwa fomu ya jumla.
- Ikiwa$A$ na$C$ sio sifuri, uwe na ishara sawa, na si sawa kwa kila mmoja, basi grafu inaweza kuwa duaradufu.
- Ikiwa$A$ na$C$ ni sawa na isiyo na sifuri na kuwa na ishara sawa, basi grafu inaweza kuwa mduara.
- Ikiwa$A$ na$C$ sio zero na zina ishara tofauti, basi grafu inaweza kuwa hyperbola.
- Ikiwa ama$A$ au$C$ ni sifuri, basi grafu inaweza kuwa parabola.

Ikiwa$B=0$, sehemu ya conic itakuwa na axes wima na/au usawa. Ikiwa$B$ haifai 0, kama inavyoonyeshwa hapo chini, sehemu ya conic imezungushwa. Angalia maneno “inaweza kuwa” katika ufafanuzi. Hiyo ni kwa sababu equation inaweza kuwakilisha sehemu conic kabisa, kulingana na maadili ya$A$$B$,$C$,$D$,$E$, na$F$. Kwa mfano, kesi iliyoharibika ya mduara au ellipse ni hatua:

\[Ax^2+By^2=0,\]

wakati$A$ na$B$ kuwa na ishara hiyo.

Kesi iliyoharibika ya hyperbola ni mistari miwili ya moja kwa moja:$Ax^2+By^2=0$, wakati$A$ na$B$ kuwa na ishara tofauti.

Kwa upande mwingine, equation$Ax^2+By^2+1=0$, wakati$A$ na$B$ ni chanya haina kuwakilisha grafu wakati wote, kwa kuwa hakuna halisi awali jozi ambayo kukidhi yake.

Mfano$\PageIndex{1}$: Identifying a Conic from Its General Form

Tambua grafu ya kila sehemu zifuatazo za nondegenerate za conic.

$4x^2−9y^2+36x+36y−125=0$
$9y^2+16x+36y−10=0$
$3x^2+3y^2−2x−6y−4=0$
$−25x^2−4y^2+100x+16y+20=0$

Suluhisho

Kuandika upya fomu ya jumla (Equation\ ref {gen}), tuna\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 125 ) &= 0 \end{align*}\]$A=4$ na$C=−9$, hivyo tunaona hilo$A$ na$C$ kuwa na ishara tofauti. Grafu ya equation hii ni hyperbola.
Kuandika upya fomu ya jumla (Equation\ ref {gen}), tuna\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 10 ) &= 0 \end{align*}\]$A=0$ na$C=9$. Tunaweza kuamua kwamba equation ni parabola, tangu$A$ ni sifuri.
Kuandika upya fomu ya jumla (Equation\ ref {gen}), tuna\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) &= 0 \end{align*}\]$A=3$ na$C=3$. Kwa sababu$A=C$, grafu ya equation hii ni mduara.
Kuandika upya fomu ya jumla (Equation\ ref {gen}), tuna\[\begin{align*} \color{red}{A} \color{black}x ^ { 2 } + \color{blue}{B} \color{black}x y + \color{red}{C} \color{black} y ^ { 2 } + \color{blue}{D} \color{black} x + \color{blue}{E} \color{black} y + \color{blue}{F} \color{black} &= 0 \\[4pt] ( - 25 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 100 x + 16 y + 20 &= 0 \end{align*}\]$A=−25$ na$C=−4$. Kwa sababu$AC>0$ na$A≠C$, grafu ya equation hii ni duaradufu.

Zoezi$\PageIndex{1}$

Tambua grafu ya kila sehemu zifuatazo za nondegenerate za conic.

$16y^2−x^2+x−4y−9=0$
$16x^2+4y^2+16x+49y−81=0$

Jibu: hyperbola
Jibu b: duaradufu

Kutafuta Uwakilishi Mpya wa Ulinganisho uliotolewa baada ya Kupokezana kupitia Angle iliyotolewa

Hadi sasa, tumeangalia usawa wa sehemu za conic bila$xy$ muda, ambayo inaunganisha grafu na x - na y -axes. Tunapoongeza$xy$ neno, tunazunguka conic kuhusu asili. Ikiwa x - na y -axes huzungushwa kupitia pembe, sema$\theta$, basi kila hatua kwenye ndege inaweza kufikiriwa kuwa na uwakilishi wawili:$(x,y)$ kwenye ndege ya Cartesian na x -axis ya awali na y -axis, na$(x^\prime ,y^\prime )$ kwenye ndege mpya inavyoelezwa na axes mpya, zinazozungushwa, inayoitwa x' -axis na y-axis (Kielelezo$\PageIndex{3}$).

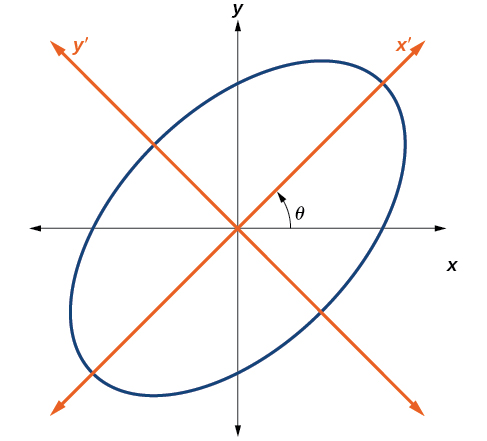
$CNX_Precalc_Figure_10_04_003.jpg$

Kielelezo$\PageIndex{3}$: Grafu ya ellipse iliyozungushwa$x^2+y^2–xy–15=0$

Tutapata uhusiano kati$x$ na$y$ kwenye ndege ya Cartesian$x^\prime $ na$y^\prime $ kwenye ndege mpya iliyozungushwa (Kielelezo$\PageIndex{4}$).

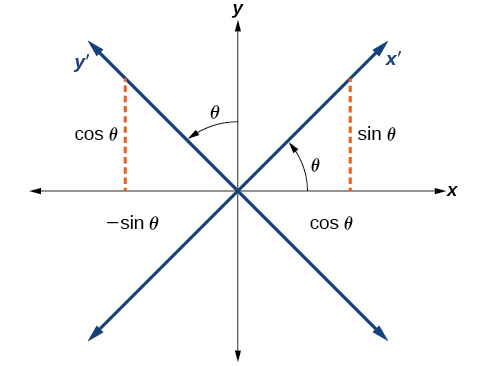
$CNX_Precalc_Figure_10_04_004.jpg$

Kielelezo$\PageIndex{4}$: Ndege ya Cartesian na$x$ - na$y$ -axes na$x^\prime$ kusababisha - na$y^\prime$ -axes zinazoundwa na mzunguko kwa angle$\theta$.

Ya awali ya kuratibu x - na y -axes ina vectors kitengo$\hat{i}$ na$\hat{j}$. Axes ya kuratibu iliyozunguka ina vectors$\hat{i}^\prime$ kitengo$\hat{j}^\prime$ na.Angle$\theta$ inajulikana kama angle ya mzunguko (Kielelezo$\PageIndex{5}$). Tunaweza kuandika vectors mpya ya kitengo kulingana na wale wa awali.

\[\hat{i}′=\cos \theta \hat{i}+\sin \theta \hat{j}\]

\[\hat{j}′=−\sin \theta \hat{i}+\cos \theta \hat{j}\]

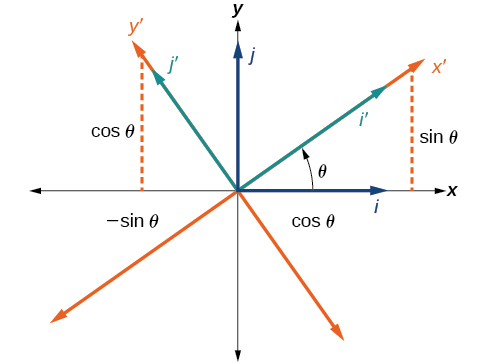
$CNX_Precalc_Figure_10_04_005.jpg$

Kielelezo$\PageIndex{5}$: Uhusiano kati ya ndege za zamani na mpya za kuratibu.

Fikiria vector$\vec{u}$ katika ndege mpya ya kuratibu. Inaweza kuwakilishwa kwa suala la axes zake za kuratibu.

\[\begin{align*} \vec{u}&=x^\prime i′+y^\prime j′ \\[4pt] &=x^\prime (i \cos \theta+j \sin \theta)+y^\prime (−i \sin \theta+j \cos \theta) & \text{Substitute.} \\[4pt] &=ix' \cos \theta+jx' \sin \theta−iy' \sin \theta+jy' \cos \theta & \text{Distribute.} \\[4pt] &=ix' \cos \theta−iy' \sin \theta+jx' \sin \theta+jy' \cos \theta & \text{Apply commutative property.} \\[4pt] &=(x' \cos \theta−y' \sin \theta)i+(x' \sin \theta+y' \cos \theta)j & \text{Factor by grouping.} \end{align*}\]

Kwa sababu$\vec{u}=x^\prime i′+y^\prime j′$, tuna uwakilishi wa$x$ na$y$ katika suala la mfumo mpya wa kuratibu.

$x=x^\prime \cos \theta−y^\prime \sin \theta$

$y=x^\prime \sin \theta+y^\prime \cos \theta$

USAWA WA MZUNGUKO

Ikiwa hatua$(x,y)$ kwenye ndege ya Cartesian inawakilishwa kwenye ndege mpya ya kuratibu ambapo shoka za mzunguko zinaundwa kwa kupokezana angle$\theta$ kutoka kwa mhimili mzuri wa x, basi kuratibu za uhakika kuhusiana na shoka mpya ni$(x^\prime ,y^\prime )$. Tunaweza kutumia equations zifuatazo za mzunguko kufafanua uhusiano kati$(x,y)$ na$(x^\prime , y^\prime )$:

\[x=x^\prime \cos \theta−y^\prime \sin \theta\]

\[y=x^\prime \sin \theta+y^\prime \cos \theta\]

Jinsi ya: Kutokana na equation ya conic, kupata uwakilishi mpya baada ya kupokezana kupitia angle

Kupata$x$ na$y$ wapi$x=x^\prime \cos \theta−y^\prime \sin \theta$ na$y=x^\prime \sin \theta+y^\prime \cos \theta$.
Badilisha maneno kwa$x$ na$y$ ndani ya equation iliyotolewa, kisha kurahisisha.
Andika equations$x^\prime $ na$y^\prime $ kwa fomu ya kawaida.

Mfano$\PageIndex{2}$: Finding a New Representation of an Equation after Rotating through a Given Angle

Kupata uwakilishi mpya wa equation$2x^2−xy+2y^2−30=0$ baada kupokezana kwa njia ya angle ya$\theta=45°$.

Suluhisho

Kupata$x$ na$y$, wapi$x=x^\prime \cos \theta−y^\prime \sin \theta$ na$y=x^\prime \sin \theta+y^\prime \cos \theta$.

Kwa sababu$\theta=45°$,

\[\begin{align*} x &= x^\prime \cos(45°)−y^\prime \sin(45°) \\[4pt] x &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right)−y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] x &=\dfrac{x^\prime −y^\prime }{\sqrt{2}} \end{align*}\]

\[\begin{align*} y &= x^\prime \sin(45°)+y^\prime \cos(45°) \\[4pt] y &= x^\prime \left(\dfrac{1}{\sqrt{2}}\right) + y^\prime \left(\dfrac{1}{\sqrt{2}}\right) \\[4pt] y &= \dfrac{x^\prime +y^\prime }{\sqrt{2}} \end{align*}\]

Mbadala$x=x^\prime \cos\theta−y^\prime \sin\theta$ na$y=x^\prime \sin \theta+y^\prime \cos \theta$ ndani ya$2x^2−xy+2y^2−30=0$.

$2{\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)}^2−\left(\dfrac{x^\prime −y^\prime }{\sqrt{2}}\right)\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)+2{\left(\dfrac{x^\prime +y^\prime }{\sqrt{2}}\right)}^2−30=0$

Kurahisisha.

$\begin{array}{rl} 2\dfrac{(x^\prime−y^\prime )(x^\prime −y^\prime )}{2}−\dfrac{(x^\prime −y^\prime )(x^\prime +y^\prime )}{2}+2\dfrac{(x^\prime +y^\prime )(x^\prime +y^\prime )}{2}−30=0 & \text{FOIL method} \\[4pt] {x^\prime }^2−2x^\prime y^\prime +{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}+{x^\prime }^2+2x^\prime y^\prime +{y^\prime }^2−30=0 & \text{Combine like terms.} \\[4pt] 2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2}=30 & \text{Combine like terms.} \\[4pt] 2(2{x^\prime }^2+2{y^\prime }^2−\dfrac{({x^\prime }^2−{y^\prime }^2)}{2})=2(30) & \text{Multiply both sides by 2.} \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−({x^\prime }^2−{y^\prime }^2)=60 & \text{Simplify. } \\[4pt] 4{x^\prime }^2+4{y^\prime }^2−{x^\prime }^2+{y^\prime }2=60 & \text{Distribute.} \\[4pt] \dfrac{3{x^\prime }^2}{60}+\dfrac{5{y^\prime }^2}{60}=\dfrac{60}{60} & \text{Set equal to 1.} \end{array} $

Andika equations$x^\prime $ na$y^\prime $ katika fomu ya kawaida.

\[\dfrac{{x^\prime }^2}{20}+\dfrac{{y^\prime}^2}{12}=1 \nonumber\]

Equation hii ni duaradufu. Kielelezo$\PageIndex{6}$ kinaonyesha grafu.

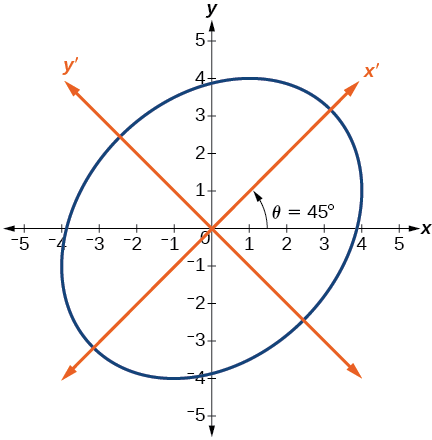
$imageedit_10_2436746571.png$

Kielelezo$\PageIndex{6}$

Kuandika Ulinganisho wa Conics iliyozunguka katika Fomu ya Standard

Sasa kwa kuwa tunaweza kupata fomu ya kawaida ya conic wakati tunapewa angle ya mzunguko, tutajifunza jinsi ya kubadilisha equation ya conic iliyotolewa katika fomu$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ katika fomu ya kawaida kwa kupokezana shoka. Ili kufanya hivyo, tutaandika upya fomu ya jumla kama equation katika mfumo$x^\prime $ na$y^\prime $ kuratibu bila$x^\prime y^\prime $ muda, kwa kupokezana shoka kwa kipimo cha$\theta$ kwamba satisfies

\[\cot(2\theta)=\dfrac{A−C}{B}\]

Tumejifunza tayari kwamba conic yoyote inaweza kuwakilishwa na equation shahada ya pili

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

ambapo$A$,$B$, na$C$ si wote sifuri. Hata hivyo, kama$B≠0$, basi tuna$xy$ muda kwamba kuzuia sisi kuandika upya equation katika hali ya kiwango. Ili kuondokana na hilo, tunaweza kugeuza axes kwa angle ya papo hapo$\theta$ ambapo$\cot(2\theta)=\dfrac{A−C}{B}$.

Kama$\cot(2\theta)>0$, basi$2\theta$ ni katika roboduara ya kwanza, na$\theta$ ni kati ya$(0°,45°)$.
Kama$\cot(2\theta)<0$, basi$2\theta$ ni katika roboduara ya pili, na$\theta$ ni kati ya$(45°,90°)$.
Ikiwa$A=C$, basi$\theta=45°$.

Jinsi ya: Kutokana na equation kwa conic katika$x^\prime y^\prime $ system, rewrite the equation without the $x^\prime y^\prime $ term in terms of $x^\prime $ and $y^\prime $,where the $x^\prime $ and $y^\prime $ axes are rotations of the standard axes by $\theta$ degrees

Kupata$\cot(2\theta)$.
Kupata$\sin \theta$ na$\cos \theta$.
Mbadala$\sin \theta$ na$\cos \theta$ ndani$x=x^\prime \cos \theta−y^\prime \sin \theta$ na$y=x^\prime \sin \theta+y^\prime \cos \theta$.
Badilisha usemi kwa$x$ na$y$ ndani ya equation iliyotolewa, na kisha kurahisisha.
Andika equations$x^\prime $ na$y^\prime $ katika fomu ya kawaida kwa heshima na axes kuzungushwa.

Mfano$\PageIndex{3}$: Rewriting an Equation with respect to the $x^\prime$ and $y^\prime$ axes without the $x^\prime y^\prime$ Term

Andika upya equation$8x^2−12xy+17y^2=20$ katika$x^\prime y^\prime $ mfumo bila$x^\prime y^\prime $ muda.

Suluhisho

Kwanza, tunapata$\cot(2\theta)$.

$8x^2−12xy+17y^2=20\rightarrow A=8$,$B=−12$ na$C=17$

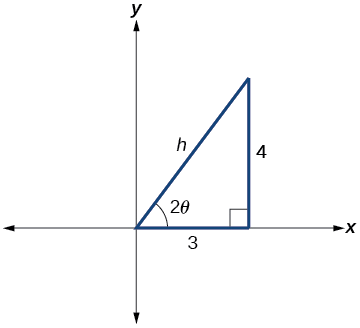
$imageedit_14_9742345318.png$

Kielelezo$\PageIndex{7}$

Kutoka Kielelezo$\PageIndex{7}$:

\[ \begin{align*} \cot(2\theta) &=\dfrac{A−C}{B}=\dfrac{8−17}{−12} \\[4pt] & =\dfrac{−9}{−12}=\dfrac{3}{4} \end{align*}\]

$\cot(2\theta)=\dfrac{3}{4}=\dfrac{\text{adjacent}}{\text{opposite}}$

Hivyo hypotenuse ni

\[ \begin{align*} 3^2+4^2 &=h^2 \\[4pt] 9+16 &=h^2 \\[4pt] 25&=h^2 \\[4pt] h&=5 \end{align*}\]

Kisha, tunapata$\sin \theta$ na$\cos \theta$.

\[ \begin{align*} \sin \theta &=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}−\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5−3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{2}{10}}=\sqrt{\dfrac{1}{5}} \\ \sin \theta &= \dfrac{1}{\sqrt{5}} \\ \cos \theta &= \sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{\dfrac{5}{5}+\dfrac{3}{5}}{2}}=\sqrt{\dfrac{5+3}{5}⋅\dfrac{1}{2}}=\sqrt{\dfrac{8}{10}}=\sqrt{\dfrac{4}{5}} \\ \cos \theta &= \dfrac{2}{\sqrt{5}} \end{align*}\]

Badilisha maadili ya$\sin \theta$ na$\cos \theta$ ndani$x=x^\prime \cos \theta−y^\prime \sin \theta$ na$y=x^\prime \sin \theta+y^\prime \cos \theta$.

\[ \begin{align*} x &=x'\cos \theta−y^\prime \sin \theta \\[4pt] &=x^\prime \left(\dfrac{2}{\sqrt{5}}\right)−y^\prime \left(\dfrac{1}{\sqrt{5}}\right) \\[4pt] &=\dfrac{2x^\prime −y^\prime }{\sqrt{5}} \end{align*}\]

\[ \begin{align*} y&=x^\prime \sin \theta+y^\prime \cos \theta \\[4pt] &=x^\prime \left(\dfrac{1}{\sqrt{5}}\right)+y^\prime \left(\dfrac{2}{\sqrt{5}}\right) \\[4pt] &=\dfrac{x^\prime +2y^\prime }{\sqrt{5}} \end{align*}\]

Badilisha maneno kwa$x$ na$y$ ndani ya equation iliyotolewa, na kisha kurahisisha.

\[ \begin{align*} 8{\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)}^2−12\left(\dfrac{2x^\prime −y^\prime }{\sqrt{5}}\right)\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)+17{\left(\dfrac{x^\prime +2y^\prime }{\sqrt{5}}\right)}^2&=20 \\[4pt] 8\left(\dfrac{(2x^\prime −y^\prime )(2x^\prime −y^\prime )}{5}\right)−12\left(\dfrac{(2x^\prime −y^\prime )(x^\prime +2y^\prime )}{5}\right)+17\left(\dfrac{(x^\prime +2y^\prime )(x^\prime +2y^\prime )}{5}\right)&=20 \\[4pt] 8(4{x^\prime }^2−4x^\prime y^\prime +{y^\prime }^2)−12(2{x^\prime }^2+3x^\prime y^\prime −2{y^\prime }^2)+17({x^\prime }^2+4x^\prime y^\prime +4{y^\prime }^2)&=100 \\[4pt] 32{x^\prime }^2−32x^\prime y^\prime +8{y^\prime }^2−24{x^\prime }^2−36x^\prime y^\prime +24{y^\prime }^2+17{x^\prime }^2+68x^\prime y^\prime +68{y^\prime }^2&=100 \\[4pt] 25{x^\prime }^2+100{y^\prime }^2&=100 \\[4pt] \dfrac{25}{100}{x^\prime }^2+\dfrac{100}{100}{y^\prime }^2&=\dfrac{100}{100} \end{align*}\]

Andika equations$x^\prime $ na$y^\prime $ katika fomu ya kawaida kwa heshima na mfumo mpya wa kuratibu.

\[\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1 \nonumber\]

Kielelezo$\PageIndex{8}$ kinaonyesha grafu ya ellipse.

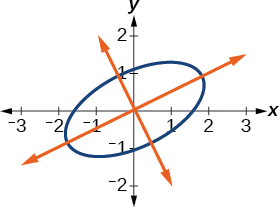
$imageedit_18_8476133234.png$

Kielelezo$\PageIndex{8}$

Zoezi$\PageIndex{2}$

Andika upya$13x^2−6\sqrt{3}xy+7y^2=16$ katika$x^\prime y^\prime $ mfumo bila$x^\prime y^\prime $ muda.

Jibu: $\dfrac{{x^\prime }^2}{4}+\dfrac{{y^\prime }^2}{1}=1$

Mfano$\PageIndex{4}$ :Graphing an Equation That Has No $x^\prime y^\prime $ Terms

Grafu equation yafuatayo kuhusiana na$x^\prime y^\prime $ mfumo:

$x^2+12xy−4y^2=30$

Suluhisho

Kwanza, tunapata$\cot(2\theta)$.

$x^2+12xy−4y^2=20\rightarrow A=1$$B=12$, na$C=−4$

\[\begin{align*} \cot(2\theta) &= \dfrac{A−C}{B} \\ \cot(2\theta) &= \dfrac{1−(−4)}{12} \\ \cot(2\theta) &= \dfrac{5}{12} \end{align*}\]

Kwa sababu$\cot(2\theta)=\dfrac{5}{12}$, tunaweza kuteka pembetatu ya kumbukumbu kama katika Kielelezo$\PageIndex{9}$.

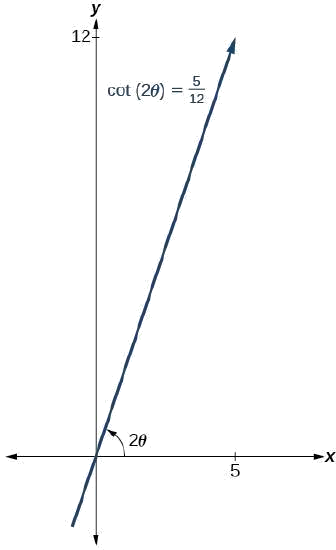
$imageedit_22_9251267068.png$

Kielelezo$\PageIndex{9}$

$\cot(2\theta)=\dfrac{5}{12}=\dfrac{adjacent}{opposite}$

Hivyo, hypotenuse ni

\[ \begin{align*} 5^2+{12}^2&=h^2 \\[4pt] 25+144 &=h^2 \\[4pt] 169 &=h^2 \\[4pt] h&=13 \end{align*}\]

Kisha, tunapata$\sin \theta$ na$\cos \theta$. Tutatumia utambulisho wa nusu ya angle.

$\sin \theta=\sqrt{\dfrac{1−\cos(2\theta)}{2}}=\sqrt{\dfrac{1−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}−\dfrac{5}{13}}{2}}=\sqrt{\dfrac{8}{13}⋅\dfrac{1}{2}}=\dfrac{2}{\sqrt{13}}$

$\cos \theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}=\sqrt{\dfrac{1+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{\dfrac{13}{13}+\dfrac{5}{13}}{2}}=\sqrt{\dfrac{18}{13}⋅\dfrac{1}{2}}=\dfrac{3}{\sqrt{13}}$

Sasa tunapata$x$ na$y$.

$x=x^\prime \cos \theta−y^\prime \sin \theta$

$x=x^\prime \left(\dfrac{3}{\sqrt{13}}\right)−y^\prime \left(\dfrac{2}{\sqrt{13}}\right)$

$x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}$

$y=x^\prime \sin \theta+y^\prime \cos \theta$

$y=x^\prime \left(\dfrac{2}{\sqrt{13}}\right)+y^\prime \left(\dfrac{3}{\sqrt{13}}\right)$

$y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}$

Sasa sisi badala$x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}$ na$y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}$ katika$x^2+12xy−4y^2=30$.

\(\begin{array}{rl} {\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)}^2+12\left(\dfrac{3x^\prime −2y^\prime }{\sqrt{13}}\right)\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)−4{\left(\dfrac{2x^\prime +3y^\prime }{\sqrt{13}}\right)}^2=30 \\ \left(\dfrac{1}{13}\right)[ {(3x^\prime −2y^\prime )}^2+12(3x^\prime −2y^\prime )(2x^\prime +3y^\prime )−4{(2x^\prime +3y^\prime )}^2 ]=30 & \text{Factor.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+12(6{x^\prime }^2+5x^\prime y^\prime −6{y^\prime }^2)−4(4{x^\prime }^2+12x^\prime y^\prime +9{y^\prime }^2) ]=30 & \text{Multiply.} \\ \left(\dfrac{1}{13}\right)[ 9{x^\prime }^2−12x^\prime y^\prime +4{y^\prime }^2+72{x^\prime }^2+60x^\prime y^\prime −72{y^\prime }^2−16{x^\prime }^2−48x^\prime y^\prime −36{y^\prime }^2 ]=30 & \text{Distribute.} \\ \left(\dfrac{1}{13}\right)[ 65{x^\prime }^2−104{y^\prime }^2 ]=30 & \text{Combine like terms.} \\ 65{x^\prime }^2−104{y^\prime }^2=390 & \text{Multiply.} \\ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 & \text{Divide by 390.} \end{array}\)

Kielelezo$\PageIndex{10}$ kinaonyesha grafu ya hyperbola$\dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1$

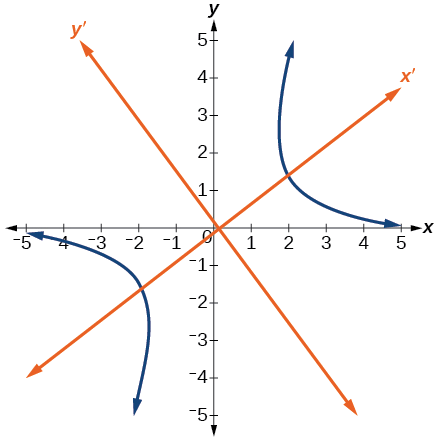
$imageedit_26_7758236974.png$

Kielelezo$\PageIndex{10}$

Kutambua Conics bila Axes zinazozunguka

Sasa tumekuja mduara kamili. Je, sisi kutambua aina ya conic ilivyoelezwa na equation? Ni nini kinachotokea wakati axes zimezungushwa? Kumbuka, fomu ya jumla ya conic ni

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

Ikiwa tunatumia fomu za mzunguko kwa equation hii, tunapata fomu.

$A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0$

Inaweza kuonyeshwa kuwa

$B^2−4AC={B′}^2−4A′C′$

Maneno hayatofautiana baada ya mzunguko, kwa hiyo tunaita maneno yasiyofaa. Wabaguzi$B^2−4AC$, hauna maana na bado haubadilika baada ya mzunguko. Kwa sababu ubaguzi bado haubadilika, kuchunguza ubaguzi hutuwezesha kutambua sehemu ya conic.

JINSI YA: KUTUMIA WABAGUZI KUTAMBUA CONIC

Kama equation

\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]

inabadilishwa na axes zinazozunguka kwenye equation

\[A′{x^\prime }^2+B′x^\prime y^\prime +C′{y^\prime }^2+D′x^\prime +E′y^\prime +F′=0\]

basi\[B^2−4AC={B′}^2−4A′C′\]

Equation$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ ni duaradufu, parabola, au hyperbola, au kesi degenerate ya mojawapo ya haya. Kama kubagua,$B^2−4AC$, ni

$<0$, sehemu ya conic ni ellipse
$=0$, sehemu ya conic ni parabola
$>0$, sehemu ya conic ni hyperbola

Mfano$\PageIndex{5}$: Identifying the Conic without Rotating Axes

Tambua conic kwa kila moja ya yafuatayo bila axes zinazozunguka.

$5x^2+2\sqrt{3}xy+2y^2−5=0$
$5x^2+2\sqrt{3}xy+12y^2−5=0$

Suluhisho

hebu tuanze kwa kuamua$A$,$B$, na$C$.

$\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{2}_{C}y^2−5=0$

Sasa, tunaona ubaguzi.

\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(2) \\ &=4(3)−40 \\ &=12−40 \\ &=−28<0 \end{align*}\]

Kwa hiyo,$5x^2+2\sqrt{3}xy+2y^2−5=0$ inawakilisha duaradufu.

b Tena, hebu tuanze kwa kuamua$A$,$B$, na$C$.

$\underbrace{5}_{A}x^2+\underbrace{2\sqrt{3}}_{B}xy+\underbrace{12}_{C}y^2−5=0 \nonumber$

Sasa, tunaona ubaguzi.

\[\begin{align*} B^2−4AC &= {(2\sqrt{3})}^2−4(5)(12) \\ &= 4(3)−240 \\ &= 12−240 \\ &=−228<0 \end{align*}\]

Kwa hiyo,$5x^2+2\sqrt{3}xy+12y^2−5=0$ inawakilisha duaradufu.

Zoezi$\PageIndex{3}$

Tambua conic kwa kila moja ya yafuatayo bila axes zinazozunguka.

$x^2−9xy+3y^2−12=0$
$10x^2−9xy+4y^2−4=0$

Jibu: hyperbola
Jibu b: duaradufu

Mlinganyo muhimu

Fomu ya jumla ya usawa wa sehemu ya conic

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

Mzunguko wa sehemu ya conic

$x=x^\prime \cos \theta−y^\prime \sin \theta$

$y=x^\prime \sin \theta+y^\prime \cos \theta$

Angle ya mzunguko

$\theta$, wapi$\cot(2\theta)=\dfrac{A−C}{B}$

Dhana muhimu

Maumbo manne ya msingi yanaweza kutokea kutokana na makutano ya ndege na jozi ya mbegu za mviringo za kulia zilizounganishwa mkia kwa mkia. Wao ni pamoja na duaradufu, mduara, hyperbola, na parabola.
Sehemu isiyo ya kawaida ya conic ina fomu ya jumla$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ ambapo$A$,$B$ na$C$ sio wote sifuri. Maadili ya$A$,$B$, na$C$ kuamua aina ya conic. Angalia Mfano$\PageIndex{1}$.
Ulinganisho wa sehemu za conic na$xy$ neno zimezungushwa kuhusu asili. Angalia Mfano$\PageIndex{2}$.
Fomu ya jumla inaweza kubadilishwa kuwa equation katika mfumo$x^\prime $ na$y^\prime $ kuratibu bila$x^\prime y^\prime $ muda. Angalia Mfano$\PageIndex{3}$ na Mfano$\PageIndex{4}$.
Maneno yanaelezewa kama yasiyofaa ikiwa bado haibadilika baada ya kupokezana. Kwa sababu kubagua ni invariant, kuchunguza inatuwezesha kutambua sehemu conic. Angalia Mfano$\PageIndex{5}$.

AINA YA JUMLA YA SEHEMU ZA CONIC

Jinsi ya: Kutokana na equation ya conic, kutambua aina ya conic

Mfano\(\PageIndex{1}\): Identifying a Conic from Its General Form

Zoezi\(\PageIndex{1}\)

USAWA WA MZUNGUKO

Jinsi ya: Kutokana na equation ya conic, kupata uwakilishi mpya baada ya kupokezana kupitia angle

Mfano\(\PageIndex{2}\): Finding a New Representation of an Equation after Rotating through a Given Angle

Jinsi ya: Kutokana na equation kwa conic katika\(x^\prime y^\prime \) system, rewrite the equation without the \(x^\prime y^\prime \) term in terms of \(x^\prime \) and \(y^\prime \),where the \(x^\prime \) and \(y^\prime \) axes are rotations of the standard axes by \(\theta\) degrees

Mfano\(\PageIndex{3}\): Rewriting an Equation with respect to the \(x^\prime\) and \(y^\prime\) axes without the \(x^\prime y^\prime\) Term

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{4}\) :Graphing an Equation That Has No \(x^\prime y^\prime \) Terms

JINSI YA: KUTUMIA WABAGUZI KUTAMBUA CONIC

Mfano\(\PageIndex{5}\): Identifying the Conic without Rotating Axes

Zoezi\(\PageIndex{3}\)

Sehemu za Conic	Mfano
duaradufu	\(4x^2+9y^2=1\)
mduara	\(4x^2+4y^2=1\)
hyperbola	\(4x^2−9y^2=1\)
parabola	\(4x^2=9y\)au\(4y^2=9x\)
mstari mmoja	\(4x+9y=1\)
mistari ya kuingiliana	\((x−4)(y+4)=0\)
mistari sambamba	\((x−4)(x−9)=0\)
uhakika	\(4x^2+4y^2=0\)
hakuna grafu	\(4x^2+4y^2=−1\)

**Jedwali\(\PageIndex{2}\)**
duaradufu	\(Ax^2+Cy^2+Dx+Ey+F=0\),\(A≠C\) na\(AC>0\)
mduara	\(Ax^2+Cy^2+Dx+Ey+F=0\),\(A=C\)
hyperbola	\(Ax^2−Cy^2+Dx+Ey+F=0\)au\(−Ax^2+Cy^2+Dx+Ey+F=0\), wapi\(A\) na\(C\) ni chanya
parabola	\(Ax^2+Dx+Ey+F=0\)au\(Cy^2+Dx+Ey+F=0\)