10.3: Parabola

Malengo ya kujifunza

• Grafu parabolas na vertices katika asili.
• Andika equations ya parabolas katika fomu ya kawaida.
• Graph parabolas na vertices si katika asili.
• Tatua matatizo yaliyotumika yanayohusisha parabolas.

Je! Unajua kwamba tochi ya Olimpiki inawaka miezi kadhaa kabla ya kuanza kwa michezo? Njia ya sherehe ya taa ya moto ni sawa na katika nyakati za kale. Sherehe hufanyika katika Hekalu la Hera huko Olympia, Ugiriki, na ni mizizi katika hadithi za Kigiriki, kulipa kodi kwa Prometheus, ambaye aliiba moto kutoka Zeus kutoa kwa wanadamu wote. Mmoja wa makuhani kumi na mmoja wa kaimu huweka tochi kwenye mtazamo wa kioo cha parabolic (Kielelezo$\PageIndex{1}$), ambacho kinalenga mionzi ya jua kutoka jua ili kuwaka moto.

Kielelezo$\PageIndex{1}$: Mwenge wa Olimpiki huhitimisha safari yake duniani kote wakati unatumiwa kuangaza chupa ya Olimpiki wakati wa sherehe ya ufunguzi. (mikopo: Ken Hackman, US Air Force)

Vioo vya parabolic (au kutafakari) vinaweza kukamata nishati na kuzingatia kwa hatua moja. Faida za mali hii zinathibitishwa na orodha kubwa ya vitu vya parabolic tunayotumia kila siku: sahani za satelaiti, madaraja ya kusimamishwa, darubini, vipaza sauti, spotlights, na vichwa vya gari, kwa jina la wachache. Reflectors parabolic pia hutumiwa katika vifaa mbadala vya nishati, kama vile cookers ya jua na hita za maji, kwa sababu ni gharama nafuu kutengeneza na wanahitaji matengenezo kidogo. Katika sehemu hii tutachunguza parabola na matumizi yake, ikiwa ni pamoja na gharama nafuu, miundo ya nishati ya jua yenye ufanisi.

Graphing Parabolas na Vertices katika Mwanzo

Hapo awali, tuliona kwamba duaradufu hutengenezwa wakati ndege inapungua kupitia koni ya mviringo sahihi. Ikiwa ndege ni sawa na makali ya koni, curve isiyofunguliwa huundwa. Curve hii ni parabola (Kielelezo$\PageIndex{2}$).

Kielelezo$\PageIndex{2}$: Parabola

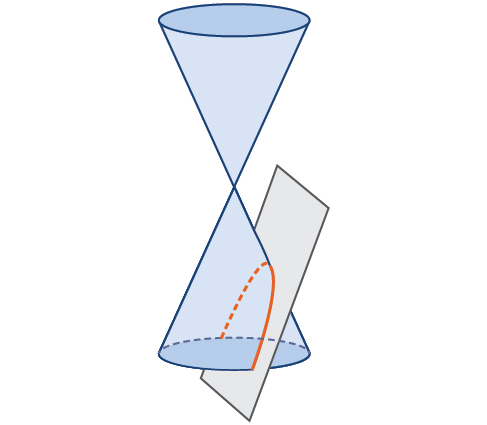
Kama duaradufu na hyperbola, parabola pia inaweza kuelezwa na seti ya pointi katika ndege ya kuratibu. Parabola ni seti ya pointi zote$(x,y)$ katika ndege ambayo ni umbali sawa kutoka kwenye mstari uliowekwa, unaoitwa directrix, na hatua ya kudumu (lengo) sio kwenye directrix.

Hapo awali, tulijifunza kuhusu vertex ya parabola na mhimili wa ulinganifu. Sasa sisi kupanua majadiliano ni pamoja na sifa nyingine muhimu ya parabola (Kielelezo$\PageIndex{3}$). Angalia kwamba mhimili wa ulinganifu hupita kupitia lengo na vertex na ni perpendicular kwa directrix. Vertex ni midpoint kati ya directrix na lengo. Sehemu ya mstari ambayo hupita kupitia lengo na inafanana na directrix inaitwa latus rectum. Mwisho wa rectum latus uongo juu ya curve. Kwa ufafanuzi, d mbali na lengo kwa hatua yoyote$P$ juu ya parabola ni sawa na umbali kutoka$P$ kwa directrix.

Kielelezo$\PageIndex{3}$: Vipengele muhimu vya parabola

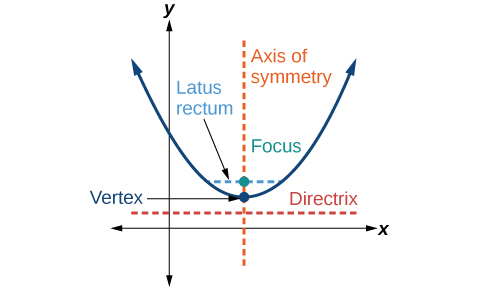
Kufanya kazi na parabolas katika ndege ya kuratibu, tunazingatia kesi mbili: wale walio na vertex katika asili na wale walio na vertex kwa hatua nyingine isipokuwa asili. Tunaanza na wa zamani.

Kielelezo$\PageIndex{4}$

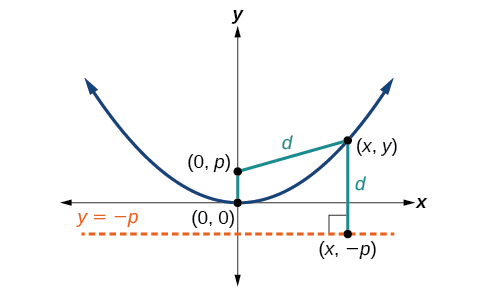
Hebu$(x,y)$ kuwa hatua juu ya parabola na kipeo$(0,0)$, lengo$(0,p)$, na directrix$y=−p$ kama inavyoonekana katika Kielelezo$\PageIndex{4}$. D mbali kutoka hatua$(x,y)$ kwa uhakika$(x,−p)$ juu ya directrix ni tofauti ya y -maadili:$d=y+p$. Umbali kutoka kwa lengo$(0,p)$ hadi hatua pia$(x,y)$ ni sawa$d$ na unaweza kuelezwa kwa kutumia formula ya umbali.

$$\begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*}$$

Kuweka maneno mawili kwa$d$ sawa na kila mmoja na kutatua$y$ kwa hupata equation ya parabola. Tunafanya hivyo kwa sababu umbali kutoka$(x,y)$ kwa$(0,p)$ sawa na umbali kutoka$(x,y)$ kwa$(x,−p)$.

$$\sqrt{x^2+{(y−p)}^2}=y+p$$

Sisi kisha mraba pande zote mbili za equation, kupanua masharti squared, na kurahisisha kwa kuchanganya maneno kama.

$$\begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*}$$

Ulinganyo wa parabola na kipeo$(0,0)$ ni$y^2=4px$ wakati x -axis ni mhimili wa ulinganifu na$x^2=4py$ wakati y -axis ni mhimili wa ulinganifu. Fomu hizi za kawaida hutolewa hapa chini, pamoja na grafu zao za jumla na vipengele muhimu.

AINA ZA KAWAIDA ZA PARABOLAS NA VERTEX$(0,0)$

Jedwali$\PageIndex{1}$ na Kielelezo$\PageIndex{5}$ muhtasari vipengele vya kawaida vya parabolas na vertex katika asili.

Jedwali$\PageIndex{1}$

Axis ya Ulinganifu	Mlinganyo	Focus	Directrix	Mwisho wa Latus Rectum
x -axis	$y^2=4px$	$(p, 0)$	$x=−p$	$(p, \pm 2p)$
y -axis	$x^2=4py$	$(0, p)$	$y=−p$	$(\pm 2p, p)$

Kielelezo$\PageIndex{5}$: (a) Wakati$p>0$ na mhimili wa ulinganifu ni x-axis, parabola inafungua haki. (b) Wakati$p<0$ na mhimili wa ulinganifu ni x-axis, parabola inafungua kushoto. (c) Wakati$p<0$ na mhimili wa ulinganifu ni y-axis, parabola inafungua. (d) Wakati$p<0$ na mhimili wa ulinganifu ni y-axis, parabola inafungua.

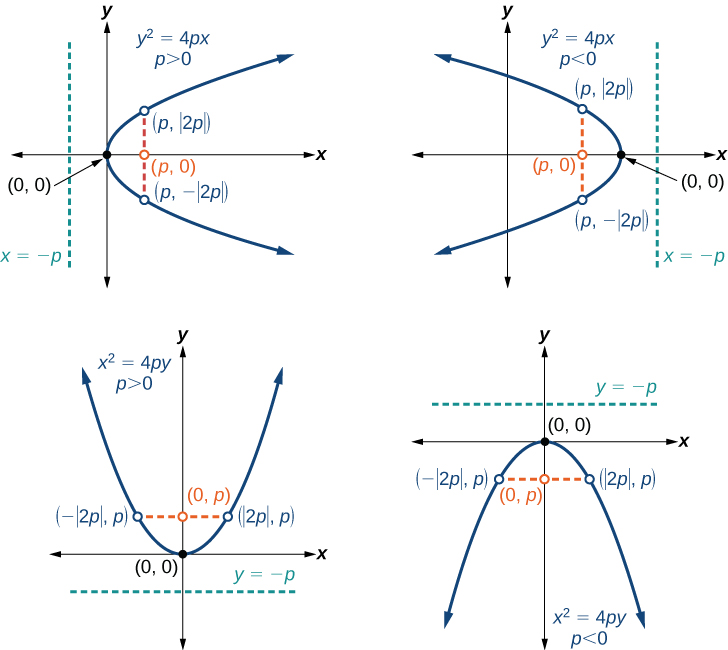
Makala muhimu ya parabola ni vertex yake, mhimili wa ulinganifu, lengo, directrix, na latus rectum (Kielelezo$\PageIndex{5}$). Wakati kupewa equation kiwango kwa parabola unaozingatia katika asili, tunaweza kwa urahisi kutambua vipengele muhimu kwa graph parabola. Mstari unasemekana kuwa tangent kwa Curve kama intersects Curve katika hatua moja hasa. Ikiwa tunachunguza mistari ya tangent kwa parabola kwenye mwisho wa rectum ya latus, mistari hii inakabiliana kwenye mhimili wa ulinganifu, kama inavyoonekana kwenye Mchoro$\PageIndex{6}$.

Kielelezo$\PageIndex{6}$

jinsi ya: Kutokana kiwango fomu equation kwa parabola unaozingatia katika$(0,0)$, sketch the graph

1. Kuamua ni aina gani ya kawaida inatumika kwa equation iliyotolewa:$y^2=4px$ au$x^2=4py$.
2. Tumia fomu ya kawaida iliyotambuliwa katika Hatua ya 1 ili kuamua mhimili wa ulinganifu, lengo, usawa wa directrix, na mwisho wa rectum ya latus.
   • Ikiwa equation iko katika fomu$y^2=4px$, basi
     • mhimili wa ulinganifu ni$x$ -axis,$y=0$
     • kuweka$4p$ sawa na mgawo wa$x$ katika equation kupewa kutatua kwa$p$. Ikiwa$p>0$, parabola inafungua haki. Ikiwa$p<0$, parabola inafungua kushoto.
     • tumia$p$ ili kupata kuratibu za lengo,$(p,0)$
     • tumia$p$ ili kupata equation ya directrix,$x=−p$
     • tumia$p$ ili kupata mwisho wa rectum ya latus,$(p,\pm 2p)$. Vinginevyo, mbadala$x=p$ katika equation ya awali.
   • Ikiwa equation iko katika fomu$x^2=4py$, basi
     • mhimili wa ulinganifu ni$y$ -axis,$x=0$
     • kuweka$4p$ sawa na mgawo wa$y$ katika equation kupewa kutatua kwa$p$. Ikiwa$p>0$, parabola inafungua. Ikiwa$p<0$, parabola inafungua.
     • tumia$p$ ili kupata kuratibu za lengo,$(0,p)$
     • tumia$p$ ili kupata equation ya directrix,$y=−p$
     • tumia$p$ ili kupata mwisho wa rectum ya latus,$(\pm 2p,p)$
3. Plot lengo, directrix, na latus rectum, na kuteka curve laini kuunda parabola.

-axis kama Axis ya Ulinganifu

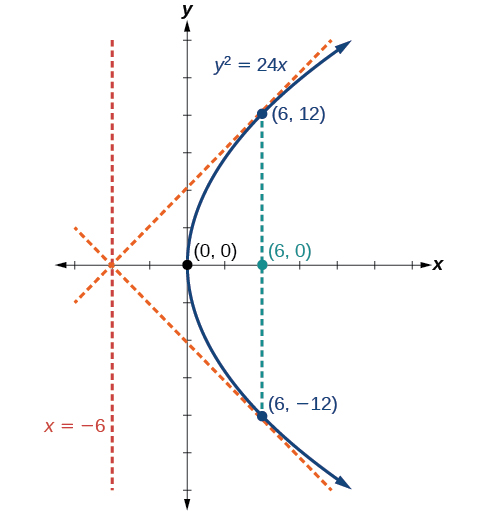
Grafu$y^2=24x$. Tambua na uweke alama ya lengo, directrix, na mwisho wa rectum ya latus.

Suluhisho

Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni$y^2=4px$. Hivyo, mhimili wa ulinganifu ni x -axis. Inafuata kwamba:

• $24=4p$, hivyo$p=6$. Tangu$p>0$, parabola inafungua haki
• kuratibu ya lengo ni$(p,0)=(6,0)$
• equation ya directrix ni$x=−p=−6$
• mwisho wa rectum ya latus una sawa x -kuratibu katika lengo. Ili kupata endpoints, mbadala$x=6$ katika equation ya awali:$(6,\pm 12)$

Halafu tunapanga lengo, directrix, na latus rectum, na kuteka curve laini ili kuunda parabola (Kielelezo$\PageIndex{7}$).

Kielelezo$\PageIndex{7}$

Zoezi$\PageIndex{1}$

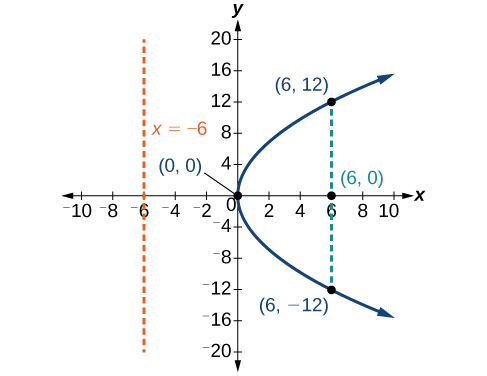
Grafu$y^2=−16x$. Tambua na uweke alama ya lengo, directrix, na mwisho wa rectum ya latus.

Jibu

• Mtazamo:$(−4,0)$
• Directrix:$x=4$
• Mwisho wa rectum ya latus:$(−4,\pm 8)$

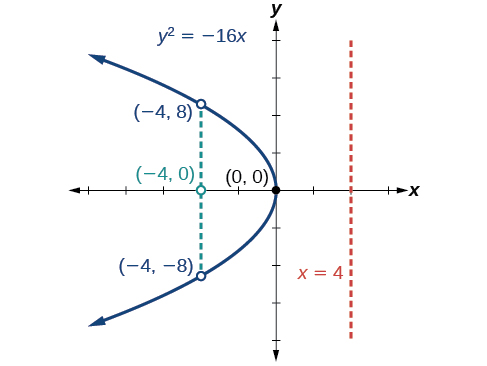
Kielelezo$\PageIndex{8}$

-axis kama Axis ya Ulinganifu

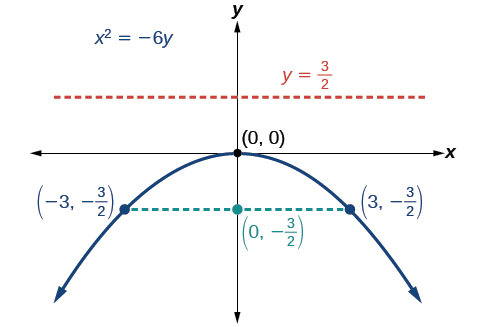
Grafu$x^2=−6y$. Tambua na uweke alama ya lengo, directrix, na mwisho wa rectum ya latus.

Suluhisho

Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni$x^2=4py$. Hivyo, mhimili wa ulinganifu ni$y$ -axis. Inafuata kwamba:

• $−6=4p$, hivyo$p=−\dfrac{3}{2}$. Tangu$p<0$, parabola inafungua.
• kuratibu ya lengo ni$(0,p)=(0,−\dfrac{3}{2})$
• equation ya directrix ni$y=−p=\dfrac{3}{2}$
• mwisho wa rectum latus unaweza kupatikana kwa kubadilisha$y=\dfrac{3}{2}$ katika equation ya awali,$(\pm 3,−\dfrac{3}{2})$

Halafu tunapanga lengo, directrix, na latus rectum, na kuteka curve laini ili kuunda parabola.

Kielelezo$\PageIndex{9}$

Zoezi$\PageIndex{2}$

Grafu$x^2=8y$. Tambua na uweke alama ya lengo, directrix, na mwisho wa rectum ya latus.

Jibu

• Mtazamo:$(0,2)$
• Directrix:$y=−2$
• Mwisho wa rectum ya latus:$(\pm 4,2)$.

Kielelezo$\PageIndex{10}$

Kuandika Ulinganisho wa Parabolas katika Fomu ya Standard

Katika mifano ya awali, tulitumia usawa wa fomu ya kawaida ya parabola ili kuhesabu maeneo ya vipengele vyake muhimu. Tunaweza pia kutumia mahesabu katika reverse kuandika equation kwa parabola wakati kupewa sifa zake muhimu.

Jinsi ya: Kutokana na mtazamo wake na directrix, kuandika equation kwa parabola katika fomu ya kawaida

1. Kuamua kama mhimili wa ulinganifu ni$x$ - au$y$ -axis.
   1. Ikiwa kuratibu zilizopewa za lengo zina fomu$(p,0)$, basi mhimili wa ulinganifu ni$x$ -axis. Tumia fomu ya kawaida$y^2=4px$.
   2. Ikiwa kuratibu zilizopewa za lengo zina fomu$(0,p)$, basi mhimili wa ulinganifu ni$y$ -axis. Tumia fomu ya kawaida$x^2=4py$.
2. Kuzidisha$4p$.
3. Badilisha thamani kutoka Hatua ya 2 kwenye usawa uliowekwa katika Hatua ya 1.

Mfano$\PageIndex{3}$: Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

Nini equation kwa parabola na lengo$(−\dfrac{1}{2},0)$ na directrix$x=\dfrac{1}{2}$?

Suluhisho

Lengo lina fomu$(p,0)$, hivyo equation itakuwa na fomu$y^2=4px$.

• Kuzidisha$4p$, tuna$4p=4(−\dfrac{1}{2})=−2$.
• Kubadilisha kwa$4p$, tuna$y^2=4px=−2x$. =

Kwa hiyo, equation kwa parabola ni$y^2=−2x$.

Zoezi$\PageIndex{3}$

Nini equation kwa parabola na lengo$\left(0,\dfrac{7}{2}\right)$ na directrix$y=−\dfrac{7}{2}$?

Jibu

$x^2=14y$.

Graphing Parabolas na Vertices Si katika Mwanzo

Kama grafu nyingine tumefanya kazi na, grafu ya parabola inaweza kutafsiriwa. Ikiwa parabola hutafsiriwa$h$ vitengo kwa usawa na$k$ vitengo kwa wima, vertex itakuwa$(h,k)$. Matokeo ya tafsiri hii katika fomu ya kawaida ya equation tuliyoona hapo awali na$x$ kubadilishwa$(x−h)$ na$y$ kubadilishwa na$(y−k)$.

Kwa grafu parabola na kipeo$(h,k)$ isipokuwa asili, tunatumia fomu ya kawaida${(y−k)}^2=4p(x−h)$ kwa parabola ambayo ina mhimili wa ulinganifu sambamba na$x$ -axis, na${(x−h)}^2=4p(y−k)$ kwa parabola zilizo na mhimili wa ulinganifu unaofanana na$y$ -axis. Fomu hizi za kawaida hutolewa hapa chini, pamoja na grafu zao za jumla na vipengele muhimu.

AINA ZA KAWAIDA ZA PARABOLAS NA VERTEX$(H, K)$

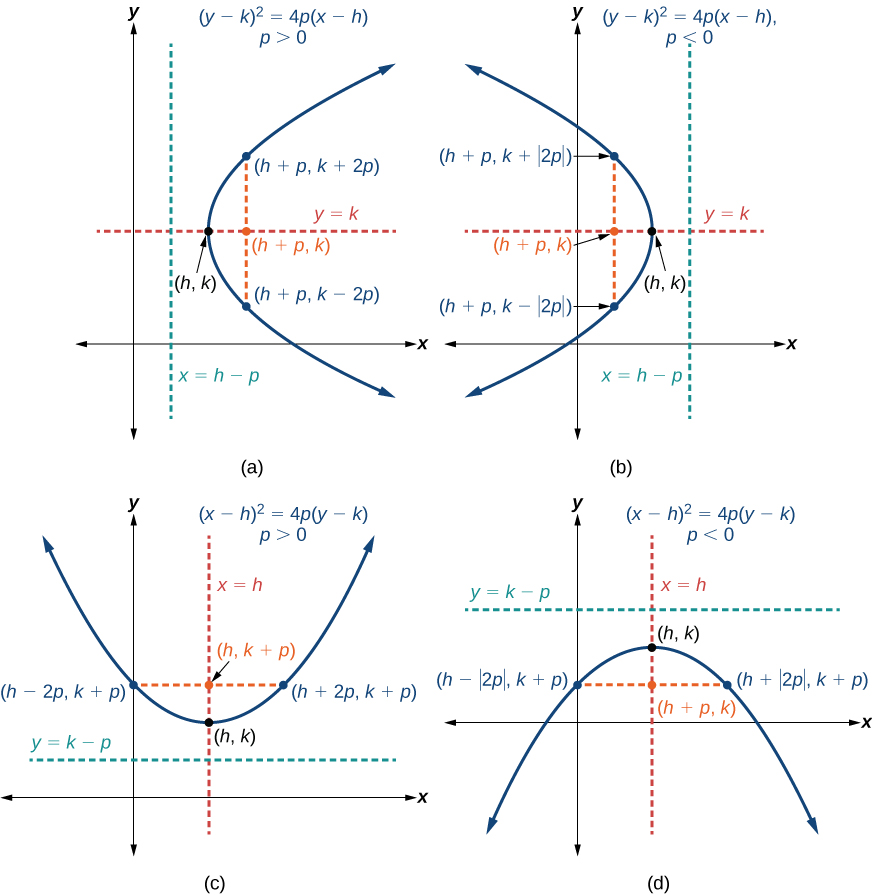
Jedwali$\PageIndex{2}$ na Kielelezo$\PageIndex{11}$ muhtasari vipengele vya kawaida vya parabolas na vertex kwa uhakika$(h,k)$.

Jedwali$\PageIndex{2}$

Axis ya Ulinganifu	Mlinganyo	Focus	Directrix	Mwisho wa Latus Rectum
$y=k$	${(y−k)}^2=4p(x−h)$	$(h+p, k)$	$x=h−p$	$(h+p, k\pm 2p)$
$x=h$	${(x−h)}^2=4p(y−k)$	$(h, k+p)$	$y=k−p$	$(h\pm 2p, k+p)$

Kielelezo$\PageIndex{11}$: (a) Wakati$p>0$, parabola inafungua haki. (b) Wakati$p<0$, parabola inafungua kushoto. (c) Wakati$p>0$, parabola inafungua. (d) Wakati$p<0$, parabola inafungua.

jinsi ya: Kutokana kiwango fomu equation kwa parabola unaozingatia katika$(h,k)$, sketch the graph

1. Kuamua ni aina gani ya kawaida inatumika kwa equation iliyotolewa:${(y−k)}^2=4p(x−h)$ au${(x−h)}^2=4p(y−k)$.
2. Tumia fomu ya kawaida iliyotambuliwa katika Hatua ya 1 ili kuamua kipeo, mhimili wa ulinganifu, lengo, usawa wa directrix, na mwisho wa rectum ya latus.
   • Ikiwa equation iko katika fomu${(y−k)}^2=4p(x−h)$, basi:
     • tumia equation iliyotolewa ili kutambua$h$ na$k$ kwa vertex,$(h,k)$
     • kutumia thamani ya$k$ kuamua mhimili wa ulinganifu,$y=k$
     • kuweka$4p$ sawa na mgawo wa$(x−h)$ katika equation kupewa kutatua kwa$p$. Ikiwa$p>0$, parabola inafungua haki. Ikiwa$p<0$, parabola inafungua kushoto.
     • kutumia$h$$k$,, na$p$ kupata kuratibu ya lengo,$(h+p, k)$
     • tumia$h$ andp ili kupata equation ya directrix,$x=h−p$
     • kutumia$h$,$k$, na$p$ kupata mwisho wa rectum latus,$(h+p,k\pm 2p)$
   • Ikiwa equation iko katika fomu${(x−h)}^2=4p(y−k)$, basi:
     • tumia equation iliyotolewa ili kutambua$h$ na$k$ kwa vertex,$(h,k)$
     • kutumia thamani ya$h$ kuamua mhimili wa ulinganifu,$x=h$
     • kuweka$4p$ sawa na mgawo wa$(y−k)$ katika equation kupewa kutatua kwa$p$. Ikiwa$p>0$, parabola inafungua. Ikiwa$p<0$, parabola inafungua.
     • kutumia$h$$k$,, na$p$ kupata kuratibu ya lengo,$(h, k+p)$
     • kutumia$k$ na$p$ kupata equation ya directrix,$y=k−p$
     • kutumia$h$,$k$, na$p$ kupata mwisho wa rectum latus,$(h\pm 2p, k+p)$
3. Panda vertex, mhimili wa ulinganifu, lengo, directrix, na latus rectum, na kuteka curve laini ili kuunda parabola.

Mfano$\PageIndex{4}$: Graphing a Parabola with Vertex $(h, k)$ and Axis of Symmetry Parallel to the $x$-axis

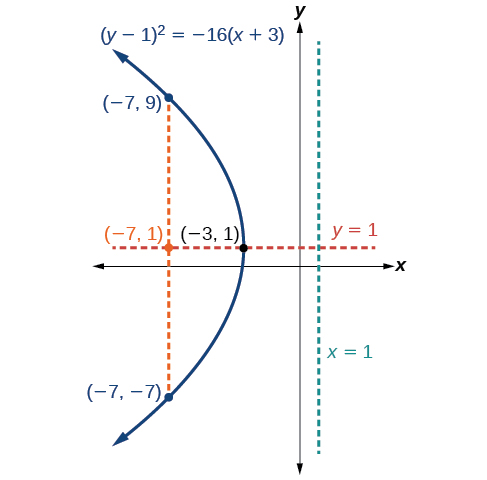
Grafu${(y−1)}^2=−16(x+3)$. Tambua na uandike kipeo, mhimili wa ulinganifu, lengo, directrix, na mwisho wa rectum ya latus.

Suluhisho

Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni${(y−k)}^2=4p(x−h)$. Hivyo, mhimili wa ulinganifu ni sawa na$x$ -axis. Inafuata kwamba:

• kipeo ni$(h,k)=(−3,1)$
• mhimili wa ulinganifu ni$y=k=1$
• $−16=4p$, hivyo$p=−4$. Tangu$p<0$, parabola inafungua kushoto.
• kuratibu ya lengo ni$(h+p,k)=(−3+(−4),1)=(−7,1)$
• equation ya directrix ni$x=h−p=−3−(−4)=1$
• mwisho wa rectum latus ni$(h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))$, au$(−7,−7)$ na$(−7,9)$

Halafu tunapanga vertex, mhimili wa ulinganifu, lengo, directrix, na latus rectum, na kuteka curve laini ili kuunda parabola (Kielelezo$\PageIndex{10}$).

Kielelezo$\PageIndex{12}$

Zoezi$\PageIndex{4}$

Grafu${(y+1)}^2=4(x−8)$. Tambua na uandike kipeo, mhimili wa ulinganifu, lengo, directrix, na mwisho wa rectum ya latus.

Jibu

• Vertex:$(8,−1)$
• Axis ya ulinganifu:$y=−1$
• Mtazamo:$(9,−1)$
• Directrix:$x=7$
• Mwisho wa rectum ya latus:$(9,−3)$ na$(9,1)$.

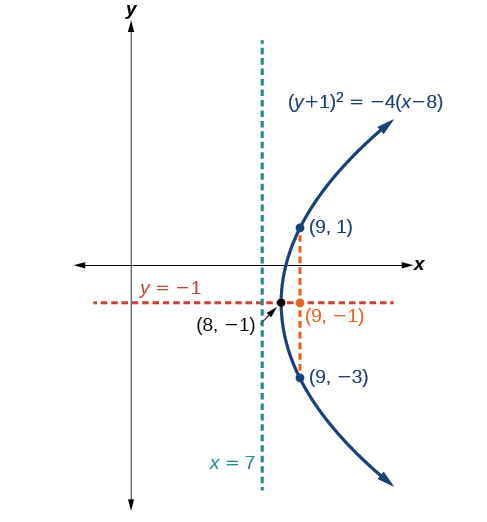
Kielelezo$\PageIndex{13}$

Mfano$\PageIndex{5}$: Graphing a Parabola from an Equation Given in General Form

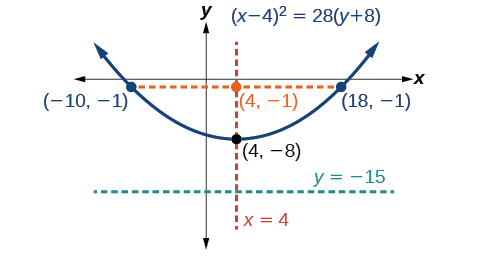
Grafu$x^2−8x−28y−208=0$. Tambua na uandike kipeo, mhimili wa ulinganifu, lengo, directrix, na mwisho wa rectum ya latus.

Suluhisho

Anza kwa kuandika equation ya parabola katika fomu ya kawaida. Fomu ya kawaida ambayo inatumika kwa equation iliyotolewa ni${(x−h)}^2=4p(y−k)$. Hivyo, mhimili wa ulinganifu ni sawa na$y$ -axis. Ili kuelezea equation ya parabola katika fomu hii, tunaanza kwa kutenganisha maneno yaliyo na variable$x$ ili kukamilisha mraba.

$$\begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}$$

Inafuata kwamba:

• kipeo ni$(h,k)=(4,−8)$
• mhimili wa ulinganifu ni$x=h=4$
• tangu$p=7$,$p>0$ na hivyo parabola inafungua
• kuratibu ya lengo ni$(h,k+p)=(4,−8+7)=(4,−1)$
• equation ya directrix ni$y=k−p=−8−7=−15$
• mwisho wa rectum latus ni$(h\pm 2p,k+p)=(4\pm 2(7),−8+7)$, au$(−10,−1)$ na$(18,−1)$

Halafu tunapanga vertex, mhimili wa ulinganifu, lengo, directrix, na latus rectum, na kuteka curve laini ili kuunda parabola (Kielelezo$\PageIndex{14}$).

Kielelezo$\PageIndex{14}$

Zoezi$\PageIndex{5}$

Grafu${(x+2)}^2=−20(y−3)$. Tambua na uandike kipeo, mhimili wa ulinganifu, lengo, directrix, na mwisho wa rectum ya latus.

Jibu

• Vertex:$(−2,3)$
• Axis ya ulinganifu:$x=−2$
• Mtazamo:$(−2,−2)$
• Directrix:$y=8$
• Mwisho wa rectum ya latus:$(−12,−2)$ na$(8,−2)$.

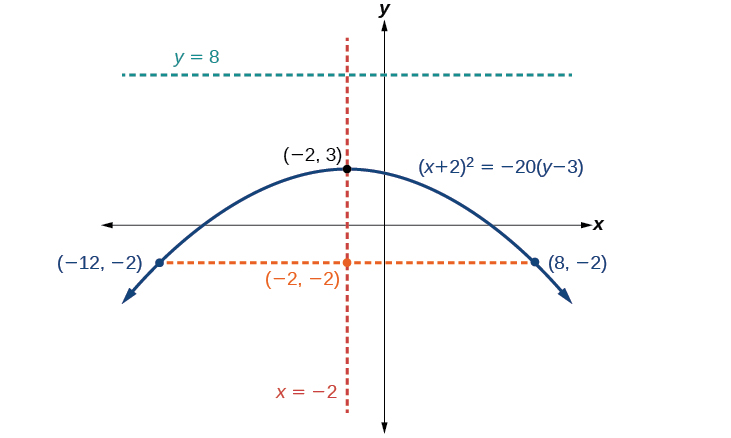
Kielelezo$\PageIndex{15}$

Kutatua Matatizo yaliyotumika Kuhusisha Parabolas

Kama tulivyosema mwanzoni mwa sehemu hiyo, parabola hutumiwa kutengeneza vitu vingi tunavyotumia kila siku, kama vile darubini, madaraja ya kusimamishwa, vipaza sauti, na vifaa vya rada. Vioo vya parabolic, kama vile vilivyotumiwa kuangaza tochi ya Olimpiki, vina mali ya kipekee ya kutafakari. Wakati mionzi ya mwanga inayofanana na mhimili wa parabola ya ulinganifu huelekezwa kuelekea uso wowote wa kioo, mwanga unaonekana moja kwa moja kwenye lengo (Kielelezo$\PageIndex{16}$). Hii ndiyo sababu tochi ya Olimpiki inapigwa moto wakati inafanyika kwenye mtazamo wa kioo cha parabolic.

Kielelezo$\PageIndex{16}$: Kuonyesha mali ya parabolas

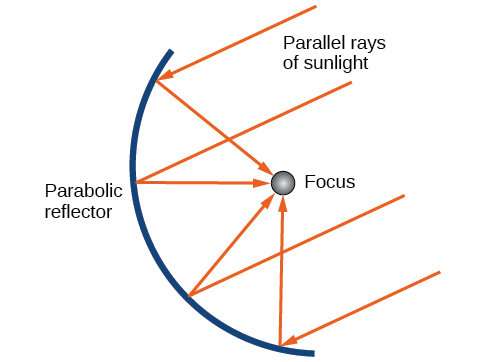
Vioo vya parabolic vina uwezo wa kuzingatia nishati ya jua kwa hatua moja, na kuongeza joto mamia ya digrii katika suala la sekunde. Hivyo, vioo vya parabolic vinatokana na bidhaa nyingi za gharama nafuu za nishati ya jua, kama vile cookers za jua, hita za jua, na hata nyota za moto za usafiri.

Mfano$\PageIndex{6}$: Solving Applied Problems Involving Parabolas

Sehemu ya msalaba wa kubuni kwa starter ya moto ya jua ya ukubwa wa usafiri inavyoonyeshwa kwenye Mchoro$\PageIndex{17}$. Mionzi ya jua huonyesha kioo cha parabolic kuelekea kitu kilichounganishwa na kupuuza. Kwa sababu kupuuza iko kwenye lengo la parabola, mionzi iliyojitokeza husababisha kitu kuchoma kwa sekunde tu.

1. Find equation ya parabola kwamba mifano ya starter moto. Fikiria kwamba vertex ya kioo cha parabolic ni asili ya ndege ya kuratibu.
2. Matumizi equation kupatikana katika sehemu (a) kupata kina cha starter moto.

Kielelezo$\PageIndex{17}$ Sehemu ya msalaba wa nyota ya moto ya jua ya ukubwa wa usafiri

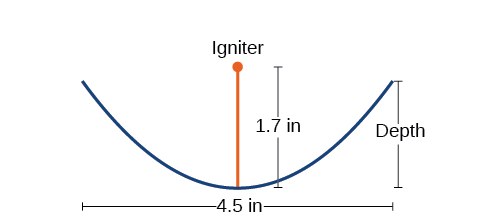
Suluhisho

1. Vertex ya sahani ni asili ya ndege ya kuratibu, hivyo parabola itachukua fomu ya kawaida$x^2=4py$, wapi$p>0$. Igniter, ambayo ni lengo, ni$1.7$ inchi juu ya vertex ya sahani. Hivyo tuna$p=1.7$.

$$\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}$$

2. Sahani huongeza$\dfrac{4.5}{2}=2.25$ inchi upande wowote wa asili. Tunaweza kuchukua nafasi$2.25$$x$ katika equation kutoka sehemu (a) ili kupata kina cha sahani.

$$\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}$$

Safu ni kuhusu$0.74$ inchi kirefu.

Zoezi$\PageIndex{6}$

Wafanyabiashara wa jua wenye ukubwa wa balcony wameundwa kwa ajili ya familia zinazoishi India. Juu ya sahani ina kipenyo cha$1600$ mm. Mionzi ya jua huonyesha kioo cha parabolic kuelekea “mpishi,” ambayo huwekwa$320$ mm kutoka msingi.

1. Pata usawa unaofanana na sehemu ya msalaba wa mpishi wa jua. Fikiria kwamba kipeo cha kioo cha paraboliki ni asili ya ndege ya kuratibu, na kwamba parabola inafungua kwa kulia (yaani, ina x -axis kama mhimili wake wa ulinganifu).
2. Tumia equation iliyopatikana katika sehemu (a) ili kupata kina cha mpishi.

Jibu

$y^2=1280x$

Jibu b

Ya kina cha mpishi ni$500$ mm

Mlinganyo muhimu

Parabola, vertex katika asili, mhimili wa ulinganifu juu ya x -axis	$y^2=4px$
Parabola, vertex katika asili, mhimili wa ulinganifu juu ya y -axis	$x^2=4py$
Parabola, vertex saa$(h,k)$, mhimili wa ulinganifu kwenye x -axis	${(y−k)}^2=4p(x−h)$
Parabola, vertex saa$(h,k)$, mhimili wa ulinganifu juu ya y -axis	${(x−h)}^2=4p(y−k)$

Dhana muhimu

• Parabola ni seti ya pointi zote$(x,y)$ katika ndege ambayo ni umbali sawa kutoka kwenye mstari uliowekwa, unaoitwa directrix, na hatua ya kudumu (lengo) sio kwenye directrix.
• Aina ya kawaida ya parabola na vertex$(0,0)$ na x -axis kama mhimili wake wa ulinganifu inaweza kutumika kwa grafu parabola. Ikiwa$p>0$, parabola inafungua haki. Ikiwa$p<0$, parabola inafungua kushoto. Angalia Mfano$\PageIndex{1}$.
• Aina ya kawaida ya parabola na vertex$(0,0)$ na y -axis kama mhimili wake wa ulinganifu inaweza kutumika kwa grafu parabola. Ikiwa$p>0$, parabola inafungua. Ikiwa$p<0$, parabola inafungua. Angalia Mfano$\PageIndex{2}$.
• Wakati kupewa lengo na directrix ya parabola, tunaweza kuandika equation yake katika fomu ya kawaida. Angalia Mfano$\PageIndex{3}$.
• Aina ya kawaida ya parabola na vertex$(h,k)$ na mhimili wa ulinganifu sambamba na$x$ -axis inaweza kutumika kwa grafu parabola. Ikiwa$p>0$, parabola inafungua haki. Ikiwa$p<0$, parabola inafungua kushoto. Angalia Mfano$\PageIndex{4}$.
• Aina ya kawaida ya parabola na vertex$(h,k)$ na mhimili wa ulinganifu sambamba na$y$ -axis inaweza kutumika kwa grafu parabola. Ikiwa$p>0$, parabola inafungua. Ikiwa$p<0$, parabola inafungua. Angalia Mfano$\PageIndex{5}$.
• Hali halisi ya ulimwengu inaweza kutengenezwa kwa kutumia equations ya kawaida ya parabolas. Kwa mfano, kutokana na kipenyo na lengo la sehemu ya msalaba wa kutafakari parabolic, tunaweza kupata equation kwamba mfano pande zake. Angalia Mfano$\PageIndex{6}$.