Skip to main content
Global

7.3: Theorem ya Kati ya Kikomo kwa Sums

  1. Last updated
  2. Save as PDF
  • Page ID
    181437

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Tuseme\(X\) ni variable random na usambazaji ambayo inaweza kujulikana au haijulikani (inaweza kuwa usambazaji wowote) na tuseme:

    • \(\mu_{x}\)= maana ya\(X\)
    • \(\sigma_{x}\)= kupotoka kwa kiwango cha\(X\)

    Kama kuteka sampuli random ya ukubwa\(n\), basi kama\(n\) ongezeko, variable random\(\sum X\) yenye kiasi huelekea kuwa kawaida kusambazwa na

    \[\sum X \sim N((n)(\mu_{x}), (\sqrt{n})(\sigma_{x})).\]

    Theorem ya kikomo ya kati kwa kiasi inasema kwamba ikiwa utaendelea kuchora sampuli kubwa na kubwa na kuchukua kiasi chao, kiasi huunda usambazaji wao wa kawaida (usambazaji wa sampuli), ambayo inakaribia usambazaji wa kawaida kama ukubwa wa sampuli huongezeka. Usambazaji wa kawaida una maana sawa na maana ya awali inayoongezeka kwa ukubwa wa sampuli na kupotoka kwa kiwango sawa na kupotoka kwa kiwango cha awali kilichoongezeka kwa mizizi ya mraba ya ukubwa wa sampuli.

    variable random\(\sum X\) ina zifuatazo z -alama zinazohusiana na hayo:

    1. \(\sum x\)ni jumla moja.
    2. \(z = \frac{\sum x - (n)(\mu_{x})}{(\sqrt{n})(\sigma_{x})}\)
      1. \((n)(\mu_{x})\)= maana ya\(\sum X\)
      2. \((\sqrt{n})(\sigma_{x})\)= kiwango kupotoka ya\(\sum X\)

    Kikokotoo

    Ili kupata uwezekano wa jumla kwenye calculator, fuata hatua hizi.

    2 na DISTRA

    2: normcdf
     normalcdf (thamani ya chini ya eneo hilo, thamani ya juu ya eneo hilo, (\(n\)) (maana), (\(\sqrt{n}\)) (kiwango cha kupotoka))

    ambapo:

    • maana ni maana ya usambazaji wa awali
    • kiwango kupotoka ni kupotoka kiwango cha usambazaji wa awali
    • ukubwa wa sampuli\(= n\)

    Mfano\(\PageIndex{1}\)

    Usambazaji usiojulikana una maana ya 90 na kupotoka kwa kiwango cha 15. Sampuli ya ukubwa 80 hutolewa nasibu kutoka kwa idadi ya watu.

    1. Pata uwezekano kwamba jumla ya maadili 80 (au jumla ya maadili 80) ni zaidi ya 7,500.
    2. Pata jumla ambayo ni upungufu wa kiwango cha 1.5 juu ya maana ya kiasi.

    Jibu

    Hebu thamani\(X =\) moja kutoka kwa idadi ya awali haijulikani. Swali la uwezekano linakuomba kupata uwezekano wa jumla (au jumla ya) maadili 80.

    \(\sum X =\)jumla au jumla ya maadili 80. Tangu\(\mu_{x} = 90\),\(\sigma_{x} = 15\), na\(n = 80\),\(\sum X \sim N((80)(90),(\sqrt{80})(15))\)

    • maana ya kiasi\(= (n)(\mu_{x}) = (80)(90) = 7,200\)
    • kiwango kupotoka kwa kiasi\(= (\sqrt{n})(\sigma_{x}) = (\sqrt{80})(15) = (80)(15)\)
    • jumla ya maadili 80\(= \sum X = 7,500\)

    a. kupata\(P(\sum X > 7,500)\)

    \(P(\sum X > 7,500) = 0.0127\)

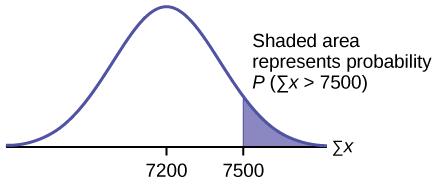
    Hii ni kawaida usambazaji Curve. Upeo wa curve unafanana na hatua ya 7200 kwenye mhimili usio na usawa. Hatua ya 7500 pia imeandikwa. Mstari wa wima unatoka hatua ya 7500 hadi kwenye pembe. Eneo la kulia la 7500 chini ya pembe ni kivuli.
    Kielelezo\(\PageIndex{1}\).

    normcdf (thamani ya chini, thamani ya juu, maana ya kiasi, stdev ya kiasi)

    Orodha ya parameter inafupishwa\(\left(lower, upper, (n)(\mu_{x}, (\sqrt{n}(\sigma_{x})\right)\)

    kawaidacf\(\left(7500,1E99,(80)(90),(\sqrt{80})(15)\right) = 0.0127\)

    UKUMBUSHO

    1E99 = 10 99.

    Bonyeza ufunguo wa EE kwa E.

    b. kupata\(\sum x\) wapi\(z = 1.5\).

    \(\sum x = (n)(\nu_{x}) + (z)(\sqrt{n})(\sigma_{x}) = (80)(90) + (1.5)(\sqrt{80})(15) = 7,401.2\)

    Zoezi\(\PageIndex{1}\)

    Usambazaji usiojulikana una maana ya 45 na kupotoka kwa kiwango cha nane. Ukubwa wa sampuli ya 50 hutolewa nasibu kutoka kwa idadi ya watu. Pata uwezekano kwamba jumla ya maadili ya 50 ni zaidi ya 2,400.

    Jibu

    0.0040

    Kikokotoo

    Ili kupata asilimia ya jumla kwenye calculator, fuata hatua hizi.

    2 na DistR

    3: Katika kawaida

    \(k = \text{invNorm} (\text{area to the left of} k, (n)(\text{mean}), (\sqrt{n})(\text{standard deviation}))\)

    ambapo:

    • \(k\)ni asilimia\(k\) th
    • maana ni maana ya usambazaji wa awali
    • kiwango kupotoka ni kupotoka kiwango cha usambazaji wa awali
    • ukubwa wa sampuli\(= n\)

    Mfano\(\PageIndex{2}\)

    Katika utafiti wa hivi karibuni uliripoti Oktoba 29, 2012 kwenye Blogu ya Flurry, umri wa wastani wa watumiaji wa kibao ni miaka 34. Tuseme kupotoka kwa kawaida ni miaka 15. Sampuli ya ukubwa ni 50.

    1. Nini maana na kiwango kupotoka kwa jumla ya umri wa watumiaji kibao? Usambazaji ni nini?
    2. Pata uwezekano kwamba jumla ya umri ni kati ya miaka 1,500 na 1,800.
    3. Kupata 80 th percentile kwa jumla ya 50 umri.

    Jibu

    1. \(\mu_{x} - n\mu_{x} = 1,700\)na Usambazaji ni\(\sigma_{\sum X} = \sqrt{n}\sigma_{X} = (\sqrt{50})(15) = 106.01\)
      wa kawaida kwa kiasi kikubwa na theorem ya kikomo ya kati.
    2. \(P(1500 < \sum X < 1800) = (1,500, 1,800, (50)(34), (\sqrt{50})(15)) = 0.7974\)
    3. Hebu\(k\) = asilimia 80 th.
      \(k = (0.80,(50)(34),(\sqrt{50})(15)) = 1,789.3\)

    Zoezi\(\PageIndex{2}\)

    Katika utafiti wa hivi karibuni uliripoti Oktoba 29, 2012 kwenye Blogu ya Flurry, umri wa wastani wa watumiaji wa kibao ni miaka 35. Tuseme kupotoka kwa kawaida ni miaka kumi. Ukubwa wa sampuli ni 39.

    1. Nini maana na kiwango kupotoka kwa jumla ya umri wa watumiaji kibao? Usambazaji ni nini?
    2. Pata uwezekano kwamba jumla ya umri ni kati ya miaka 1,400 na 1,500.
    3. Kupata 90 th percentile kwa jumla ya 39 umri.

    Jibu

    1. \(\mu_{\sum X} = n\mu_{X} = 1,365\)na Usambazaji ni\(\sigma_{\sum X} = \sqrt{n}\sigma_{x} = 62.4\)
      wa kawaida kwa kiasi kikubwa na theorem ya kikomo ya kati.
    2. \(P(1400 < \sum_{X} < 1500) = \text{normalcdf} (1400,1500,(39)(35),(\sqrt{39})(10)) = 0.2723\)
    3. Hebu\(k\) = asilimia 90 th.
      \(k = \text{invNorm} (0.90,(39)(35),(\sqrt{39}) (10)) = 1445.0\)

    Mfano\(\PageIndex{3}\)

    Idadi ya dakika ya ushiriki wa programu na mtumiaji wa kibao ni dakika 8.2. Tuseme kupotoka kwa kawaida ni dakika moja. Chukua sampuli ya ukubwa 70.

    1. Nini maana na kiwango kupotoka kwa kiasi?
    2. Kupata 95 th percentile kwa jumla ya sampuli. Tafsiri thamani hii katika sentensi kamili.
    3. Pata uwezekano kwamba jumla ya sampuli ni angalau masaa kumi.

    Jibu

    1. \(\mu_{\sum X} = n\mu_{X}= 70(8.2) = 574\)dakika na\(\sigma_{\sum X} (\sqrt{n})(\sigma_{x}) = (\sqrt{70})(1) = 8.37\) dakika
    2. Hebu\(k\) = asilimia 95 th.
      \(k = \text{invNorm} (0.95,(70)(8.2),(\sqrt{70})(1)) = 587.76\)dakika
      tisini na tano asilimia ya programu mara ushiriki ni saa zaidi 587.76 dakika.
    3. masaa kumi = dakika 600
      \(P(\sum X \geq 600) = \text{normalcdf}(600,E99,(70)(8.2),(\sqrt{70})(1)) = 0.0009\)

    Zoezi\(\PageIndex{3}\)

    Idadi ya dakika ya ushiriki wa programu na matumizi ya meza ni dakika 8.2. Tuseme kupotoka kwa kawaida ni dakika moja. Chukua ukubwa wa sampuli ya 70.

    1. Ni uwezekano gani kwamba jumla ya sampuli ni kati ya masaa saba na saa kumi? Hii ina maana gani katika mazingira ya tatizo?
    2. Pata asilimia 84 na 16 th kwa jumla ya sampuli. Tafsiri maadili haya kwa muktadha.

    Jibu

    1. Masaa ya 7 = dakika 420 masaa
      10 = dakika 600
      \(\text{normalcdf} P(420 \leq \sum X \leq 600) = \text{normalcdf}(420,600,(70)(8.2),\sqrt{70}(1)) = 0.9991\)
      Hii inamaanisha kwamba kwa sampuli hii kuna nafasi ya 99.9% kwamba kiasi cha dakika ya matumizi itakuwa kati ya dakika 420 na dakika 600.
    2. \(\text{invNorm}(0.84,(70)(8.2)\),\(\sqrt{70}(1)) = 582.32\)
      \(\text{invNorm}(0.16,(70)(8.2),(\sqrt{70}(1)) = 565.68\)
      Tangu 84% ya nyakati za ushiriki wa programu ni zaidi ya dakika 582.32 na 16% ya nyakati za ushiriki wa programu ni zaidi ya dakika 565.68, tunaweza kusema kuwa 68% ya nyakati za ushiriki wa programu ni kati ya dakika 565.68 na dakika 582.32.

    Marejeo

    1. Farago, Petro. “Ukweli Kuhusu Paka na Mbwa: Smartphone vs Tablet Matumizi Tofauti.” Blog Flurry, 2013. Imetumwa Oktoba 29, 2012. Inapatikana mtandaoni kwenye blog.flurry.com (imefikia Mei 17, 2013).

    Tathmini

    Theorem ya kikomo ya kati inatuambia kwamba kwa idadi ya watu wenye usambazaji wowote, usambazaji wa kiasi cha sampuli inamaanisha usambazaji wa kawaida kama ukubwa wa sampuli huongezeka. Kwa maneno mengine, kama ukubwa wa sampuli ni kubwa ya kutosha, usambazaji wa kiasi unaweza kulinganishwa na usambazaji wa kawaida hata kama idadi ya watu asilia si kawaida kusambazwa. Zaidi ya hayo, kama idadi ya watu wa awali ina maana ya\(\mu_{x}\) na kupotoka kiwango cha\(\sigma_{x}\), maana ya kiasi ni\(n\)\(\mu_{x}\) na kupotoka kiwango ni (\(\sqrt{n}\)) (\(\sigma_{x}\)) wapi\(n\) sampuli ukubwa.

    Mapitio ya Mfumo

    • Theorem ya Kati ya Limit kwa Sums:\(\sum X ~ N[(n)(\mu_{x}, (\sqrt{n})(\sigma_{x}))]\)
    • Maana ya Sums\((\sum X): (n)(\mu_{x})\)
    • Theorem ya Kati ya Limit kwa\(z\) Sums -alama na kiwango kupotoka kwa kiasi:\(z \text{ for the sample mean} = \frac{\sum x - (n)(\mu_{x})}{(\sqrt{n})(\sigma_{x})}\)
    • Kiwango kupotoka kwa Sums\((\sum X): (\sqrt{n})(\sigma_{x})\)