7.4: Kutumia Theorem ya Kati ya Kikomo

Ni muhimu kwako kuelewa wakati wa kutumia theorem ya kikomo ya kati (clt). Ikiwa unaulizwa kupata uwezekano wa maana, tumia clt kwa maana. Kama wewe ni kuwa aliuliza kupata uwezekano wa jumla au jumla, kutumia clt kwa kiasi. Hii inatumika pia kwa asilimia kwa njia na kiasi.

Ikiwa unaulizwa kupata uwezekano wa thamani ya mtu binafsi, usitumie clt. Tumia usambazaji wa kutofautiana kwake kwa random.

Sheria ya Idadi Kubwa

Sheria ya idadi kubwa inasema kwamba ikiwa unachukua sampuli za ukubwa mkubwa na mkubwa kutoka kwa idadi yoyote ya watu, basi maana\(\bar{x}\) ya sampuli huelekea kupata karibu na karibu\(\mu\). Kutoka kati kikomo theorem, tunajua kwamba kama\(n\) anapata kubwa na kubwa, sampuli ina maana kufuata usambazaji wa kawaida. Kubwa\(n\) hupata, ndogo kupotoka kwa kiwango hupata. (Kumbuka kwamba kiwango kupotoka kwa\(\bar{X}\) ni\(\dfrac{\sigma}{\sqrt{n}}\).) Hii ina maana kwamba sampuli maana\(\bar{x}\) lazima iwe karibu na maana ya idadi ya watu\(\mu\). Tunaweza kusema kwamba\(\mu\) ni thamani kwamba sampuli ina maana mbinu kama\(n\) anapata kubwa. Theorem ya kikomo ya kati inaonyesha sheria ya idadi kubwa.

Mfano\(\PageIndex{1}\)

Utafiti unaohusisha dhiki unafanywa kati ya wanafunzi kwenye chuo cha chuo kikuu. Alama za mkazo hufuata usambazaji sare na alama ya chini kabisa ya dhiki sawa na moja na ya juu sawa na tano. Kutumia sampuli ya wanafunzi 75, tafuta:

1. uwezekano kwamba wastani stress alama kwa 75 wanafunzi ni chini ya mbili.
2. The 90 ^th percentile kwa wastani stress alama kwa 75 wanafunzi.
3. uwezekano kwamba jumla ya 75 stress alama ni chini ya 200.
4. The 90 ^th percentile kwa jumla stress alama kwa 75 wanafunzi.

Solutions

Hebu alama\(X =\) moja ya dhiki.

Matatizo a na b kuuliza wewe kupata uwezekano au percentile kwa maana. Matatizo c na d kuuliza wewe kupata uwezekano au percentile kwa jumla au jumla. Ukubwa wa sampuli\(n\),, ni sawa na 75.

Kwa kuwa alama ya dhiki ya mtu binafsi hufuata usambazaji sare,\(X \sim U(1, 5)\) wapi\(a = 1\) na\(b = 5\).

\[\mu_{x} = \dfrac{a+b}{2} = \dfrac{1+5}{2} = 3\]

\[\sigma_{x} = \sqrt{\dfrac{(b-a)^{2}}{12}} = \sqrt{\dfrac{(5-1)^{2}}{12}} = 1.15\]

Kwa matatizo 1. na 2., basi\(\bar{X} =\) wastani stress alama kwa 75 wanafunzi. Kisha,

\[\bar{X} \sim N\left(3, \dfrac{1,15}{\sqrt{75}}\right)\]

wapi\(n = 75\).

1. Kupata\(P(\bar{x} < 2)\). Chora grafu.
2. Kupata 90 ^th percentile kwa maana ya 75 alama stress. Chora grafu.
3. Kupata\(P(\sum x < 2000)\). Chora grafu.
4. Kupata 90 ^th percentile kwa jumla ya 75 alama stress. Chora grafu.

Majibu

a.\(P(\bar{x} < 2) = 0\)

Uwezekano kwamba alama ya shida ya maana ni chini ya mbili ni kuhusu sifuri.

Kielelezo\(\PageIndex{1}\).

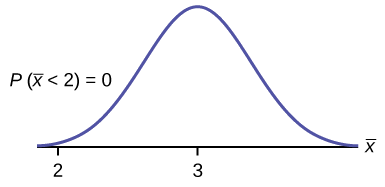
kawaidacf\(\left(1,2,3,\dfrac{1.15}{\sqrt{75}}\right) = 0\)

UKUMBUSHO

Alama ndogo zaidi ya dhiki ni moja

b Hebu\(k =\) 90 ^th percentile.

Kupata\(k\), wapi\(P(\bar{x} < k) = 0.90\).

\(k = 3.2\)

Kielelezo\(\PageIndex{2}\).

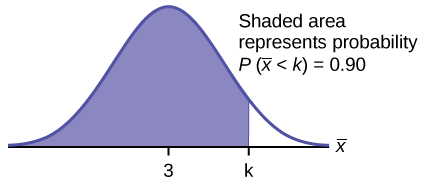
^{Asilimia ya} 90 kwa maana ya alama 75 ni karibu 3.2. Hii inatuambia kwamba 90% ya njia zote za alama za dhiki 75 ni zaidi ya 3.2, na kwamba 10% ni angalau 3.2.

isiyo ya kawaida\(\left(0.90,3,1.\dfrac{1.15}{\sqrt{75}}\right) = 3.2\)

Kwa matatizo c na d, basi jumla\(\sum X =\) ya 75 alama stress. Kisha,

\[\sum X \sim N((75)(3), (\sqrt{75})(1.15))\]

c. maana ya jumla ya alama 75 stress ni\((75)(3) = 225\)

Kupotoka kwa kiwango cha jumla ya alama 75 za dhiki ni\((\sqrt{75})(1.15) = 9.96\)

\(P(\sum x < 200)\)

Kielelezo\(\PageIndex{3}\).

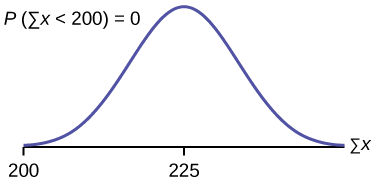
Uwezekano kwamba jumla ya alama 75 ni chini ya 200 ni kuhusu sifuri.

kawaidacf\(75,200,(75)(3),(\sqrt{75})(1.15)\).

UKUMBUSHO

Jumla ndogo zaidi ya alama za dhiki 75 ni 75, kwa sababu alama ndogo zaidi ni moja.

d Hebu\(k =\) 90 ^th percentile.

Pata\(k\) wapi\(P(\sum x < k) = 0.90\).

\(k = 237.8\)

Kielelezo\(\PageIndex{4}\).

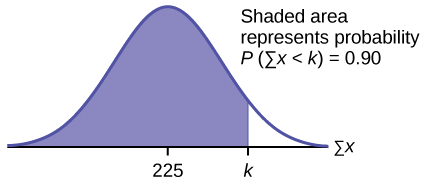
^{Asilimia ya} 90 kwa jumla ya alama 75 ni karibu 237.8. Hii inatuambia kwamba 90% ya jumla ya alama 75 sio zaidi ya 237.8 na 10% sio chini ya 237.8.

isiyo ya kawaida\(\left(0.90, (75)(3), (\sqrt{75})(1.15)\right) = 237.8\)

Zoezi\(\PageIndex{1}\)

Tumia maelezo katika Mfano\(\PageIndex{1}\), lakini tumia ukubwa wa sampuli ya 55 ili kujibu maswali yafuatayo.

1. Kupata\(P(\bar{x} < 7)\).
2. Kupata\(P(\sum x < 7)\).
3. Kupata 80 ^th percentile kwa maana ya alama 55.
4. Kupata 85 ^th percentile kwa jumla ya alama 55.

Jibu

1. 0.0265
2. 0.2789
3. 3.13
4. 173.84

Mfano\(\PageIndex{2}\)

Tuseme kwamba mchambuzi wa utafiti wa soko kwa kampuni ya simu ya mkononi inafanya utafiti wa wateja wao ambao huzidi posho wakati ni pamoja na kwenye mkataba wao wa msingi simu ya mkononi; mchambuzi anaona kwamba kwa wale watu ambao kuzidi muda ni pamoja na katika mkataba wao wa msingi, muda ziada kutumika ifuatavyo usambazaji wa kielelezo kwa maana ya dakika 22.

Fikiria sampuli random ya 80 wateja ambao kisichozidi posho wakati ni pamoja na katika mkataba wao msingi simu ya mkononi.

Hebu\(X =\) muda ziada kutumiwa na mtu binafsi simu ya mkononi mteja ambaye unazidi mkataba wake posho wakati.

\(X \sim Exp\left(\dfrac{1}{22}\right)\). Kutoka sura zilizopita, tunajua kwamba\(\mu = 22\) na\(\sigma = 22\).

Hebu\(\bar{X}\) = muda wa ziada unaotumiwa na sampuli ya\(n = 80\) wateja ambao huzidi muda wao wa mkataba wa posho.

\[\bar{X} \sim N\left(22,\dfrac{22}{\sqrt{80}}\right)\]

kwa theorem ya kikomo ya kati kwa njia ya sampuli

1. Pata uwezekano kwamba muda wa ziada unaotumiwa na wateja wa 80 katika sampuli ni mrefu zaidi ya dakika 20. Hii inatuuliza kupata\(P(\bar{x} > 20)\). Chora grafu.
2. Tuseme kwamba mteja mmoja ambaye unazidi kikomo cha muda kwa mkataba wake wa simu ya mkononi ni nasibu kuchaguliwa. Pata uwezekano kwamba muda wa ziada wa mteja huyu ni mrefu zaidi ya dakika 20. Hii inatuuliza kupata\(P(x > 20)\).
3. Eleza kwa nini probabilities katika sehemu a na b ni tofauti.
4. Kupata 95 ^th percentile kwa sampuli maana muda ziada kwa ajili ya sampuli ya 80 wateja ambao kisichozidi misaada yao ya msingi mkataba wakati. Chora grafu.

Jibu

1. Kupata:\(P(\bar{x} > 20)\)

   \(P(\bar{x} > 20) = 0.79199\)kutumia normcdf\(\left(20,1\text{E}99,22,\dfrac{22}{\sqrt{80}}\right)\)

   Uwezekano ni 0.7919 kwamba muda wa ziada unaotumiwa ni zaidi ya dakika 20, kwa sampuli ya wateja 80 ambao huzidi muda wao wa mkataba.

   20)." src="https://stats.libretexts.org/@api/de...1180/7.4.5.png">

   Kielelezo\(\PageIndex{5}\).

   UKUMBUSHO

   1E99 = 10 ⁹⁹ na —1E99 = —10 ⁹⁹. Vyombo vya habari EE muhimu kwa E. au tu kutumia 10 ⁹⁹ badala ya 1E99.

2. Kupata\(P(x > 20)\). Kumbuka kutumia usambazaji wa kielelezo kwa mtu binafsi:\(X \sim Exp\left(\dfrac{1}{22}\right)\). \(P(x > 20) = e^{(−\left(\dfrac{1}{22}\right)(20))}\)au\(e^{(–0.04545(20))} = 0.4029\)
3. 1. \(P(x > 20) = 0.4029\)lakini\(P(\bar{x} > 20) = 0.7919\)
   2. Probabilities si sawa kwa sababu tunatumia mgawanyo tofauti kuhesabu uwezekano kwa watu binafsi na kwa njia.
   3. Alipoulizwa kupata uwezekano wa thamani ya mtu binafsi, tumia usambazaji ulioelezwa wa kutofautiana kwake kwa random; usitumie clt. Matumizi clt na usambazaji wa kawaida wakati wewe ni kuwa aliuliza kupata uwezekano kwa maana.
4. Hebu\(k\) = 95 ^th percentile. Pata\(k\) wapi\(P(\bar{x} < k) = 0.95\)

   \(k = 26.0\)kutumia InvNorm\(\left(0.95,22,\dfrac{22}{\sqrt{80}}\right) = 26.0\)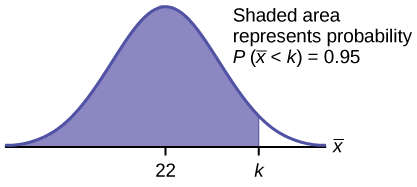

   

   Kielelezo\(\PageIndex{6}\).

   Asilimia ^ya 95 ya sampuli inamaanisha muda wa ziada unaotumiwa ni dakika 26.0 kwa sampuli za random za wateja wa 80 ambao huzidi muda wao wa kuruhusiwa mkataba.

   Asilimia tisini na tano ya sampuli hizo ingekuwa na maana chini ya dakika 26; asilimia tano tu ya sampuli hizo ingekuwa na maana zaidi ya dakika 26.

Zoezi\(\PageIndex{2}\)

Tumia maelezo katika Mfano\(\PageIndex{2}\), lakini ubadilishe ukubwa wa sampuli kwa 144.

1. Kupata\(P(20 < \bar{x} < 30)\).
2. Kupata\(P(\sum x \text{ is at least } 3,000)\).
3. Pata asilimia 75 ^ya sampuli inamaanisha muda wa ziada wa wateja wa 144.
4. Kupata 85 ^th percentile kwa jumla ya 144 nyakati ziada kutumiwa na wateja.

Jibu

1. 0.8623
2. 0.7377
3. 23.2
4. 3,441.6

Mfano\(\PageIndex{3}\)

Nchini Marekani, mtu anashambuliwa ngono kila baada ya dakika mbili, kwa wastani, kulingana na tafiti kadhaa. Tuseme kupotoka kwa kawaida ni dakika 0.5 na ukubwa wa sampuli ni 100.

1. Pata wastani, robo ya kwanza, na robo ya tatu kwa sampuli maana wakati wa mashambulizi ya kijinsia nchini Marekani.
2. Pata wastani, robo ya kwanza, na robo ya tatu kwa jumla ya nyakati za sampuli za mashambulizi ya kijinsia nchini Marekani.
3. Pata uwezekano kwamba unyanyasaji wa kijinsia hutokea kwa wastani kati ya dakika 1.75 na 1.85.
4. Kupata thamani ambayo ni mbili kiwango ukiukaji juu ya sampuli maana.
5. Pata IQR kwa jumla ya nyakati za sampuli.

Jibu

1. tuna,\(\mu_{x} = \mu = 2\) na\(\sigma_{x} = \dfrac{\sigma}{\sqrt{n}} = \dfrac{0.5}{10} = 0.05\). Kwa hiyo:
   1. ^Asilimia 50\(= \mu_{x} = \mu = 2\)
   2. ^Asilimia 25\(= \text{invNorm}(0.25,2,0.05) = 1.97\)
   3. ^Asilimia 75\(= \text{invNorm}(0.75,2,0.05) = 2.03\)
2. Tuna\(\mu_{\sum X} = n(\mu_{x}) = 100(2)\) na\(\sigma_{\mu X} = \sqrt{n}(\sigma_{x}) = 10(0.5) = 5\). Kwa hiyo
   1. 50 ^th percentile =\(\mu_{\sum X} = n(\mu_{X}) = 100(2) = 200\)
   2. ^Asilimia 25\(= \text{invNorm}(0.25,200,5) = 196.63\)
   3. ^Asilimia 75\(= \text{invNorm}(0.75,200,5) = 203.37\)
3. \(P(1.75 < bar{x} < 1.85) =\)kawaidacf\((1.75,1.85,2,0.05) = 0.0013\)
4. Kutumia equation\(z\) -score\(z = \dfrac{\bar{x} - \mu_{\bar{x}}}{\sigma_{\bar{x}}}\),, na kutatua kwa\(x\), tuna\(x = 2(0.05) + 2 = 2.1\)
5. \(IQR\)Ni 75 ^th percentile — 25 ^th percentile\(= 203.37 – 196.63 = 6.74\)

Zoezi\(\PageIndex{3}\)

Kulingana na takwimu kutoka Utafiti wa Afya ya Taifa, wanawake kati ya umri wa miaka 18 na 24 wana wastani wa shinikizo la damu systolic (katika mm Hg) ya 114.8 na kupotoka kwa kiwango cha 13.1. Shinikizo la damu la Systolic kwa wanawake kati ya umri wa miaka 18 hadi 24 hufuata usambazaji wa kawaida.

1. Ikiwa mwanamke mmoja kutoka kwa idadi hii anachaguliwa kwa nasibu, pata uwezekano kwamba shinikizo lake la damu la systolic ni kubwa kuliko 120.
2. Ikiwa wanawake 40 kutoka kwa idadi hii wanachaguliwa kwa nasibu, pata uwezekano kwamba shinikizo lao la systolic la damu ni kubwa kuliko 120.
3. Ikiwa sampuli ilikuwa wanawake wanne kati ya umri wa miaka 18 hadi 24 na hatukujua usambazaji wa awali, je, theorem ya kikomo ya kati inaweza kutumika?

Jibu

1. \(P(x > 120)\)= kawaidacdf\((120,99,114.8,13.1) = 0.0272\). Kuna kuhusu 3%, kwamba mwanamke aliyechaguliwa kwa nasibu atakuwa na systolics shinikizo la damu kubwa kuliko 120.
2. \(P(\bar{x} > 120) =\)kawaidacf\(\left(120,114.8,\dfrac{13.1}{\sqrt{40}}\right) = 0.006\). Kuna nafasi ya 0.6% tu kwamba wastani wa shinikizo la damu la systolic kwa kundi lililochaguliwa kwa nasibu ni kubwa kuliko 120.
3. Theorem ya kikomo ya kati haikuweza kutumika kama ukubwa wa sampuli ulikuwa wa nne na hatukujua usambazaji wa awali ulikuwa wa kawaida. Ukubwa wa sampuli itakuwa ndogo sana.

Mfano\(\PageIndex{4}\)

Utafiti ulifanyika kuhusu unyanyasaji dhidi ya makahaba na dalili za matatizo ya baada ya kiwewe waliyoendeleza. Mipaka ya umri wa makahaba ilikuwa 14 hadi 61. Umri wa wastani ulikuwa miaka 30.9 na kupotoka kwa kiwango cha miaka tisa.

1. Katika sampuli ya makahaba 25, ni uwezekano gani kwamba umri wa wastani wa makahaba ni chini ya 35?
2. Je, inawezekana kwamba umri wa wastani wa kundi la sampuli inaweza kuwa zaidi ya miaka 50? Tafsiri matokeo.
3. Katika sampuli ya makahaba 49, ni uwezekano gani kwamba jumla ya umri sio chini ya 1,600?
4. Je, inawezekana kwamba jumla ya umri wa makahaba 49 ni zaidi ya 1,595? Tafsiri matokeo.
5. Kupata 95 ^th asilimia kwa sampuli maana umri wa 65 makahaba. Tafsiri matokeo.
6. Kupata 90 ^th asilimia kwa jumla ya umri wa 65 makahaba. Tafsiri matokeo.

Jibu

1. \(P(\bar{x} < 35) =\)kawaidacf\((-E99,35,30.9,1.8) = 0.9886\)
2. \(P(\bar{x} > 50) =\)kawaidacf\((50, E99,30.9,1.8) \approx 0\). Kwa kundi hili la sampuli, haiwezekani kwa umri wa wastani wa kikundi kuwa zaidi ya 50. Hata hivyo, bado inawezekana kwa mtu binafsi katika kundi hili kuwa na umri mkubwa zaidi ya 50.
3. \(P(\sum x \geq 1,600) =\)kawaidacf\((1600,E99,1514.10,63) = 0.0864\)
4. \(P(\sum x \leq 1,595) =\)kawaidacf\((-E99,1595,1514.10,63) = 0.9005\). Hii ina maana kwamba kuna nafasi ya 90% kwamba jumla ya umri wa kundi la sampuli\(n = 49\) ni zaidi ya 1595.
5. Asilimia 95 = invNorm\((0.95,30.9,1.1) = 32.7\). Hii inaonyesha kwamba 95% ya makahaba katika sampuli ya 65 ni mdogo kuliko miaka 32.7, kwa wastani.
6. Asilimia ya 90 = invNorm\((0.90,2008.5,72.56) = 2101.5\). Hii inaonyesha kwamba 90% ya makahaba katika sampuli ya 65 wana jumla ya umri chini ya miaka 2,101.5.

Zoezi\(\PageIndex{4}\)

Kwa mujibu wa takwimu za Boeing, ndege ya 757 inabeba abiria 200 na ina milango yenye urefu wa inchi 72. Fikiria kwa idadi fulani ya wanaume tuna maana ya inchi 69.0 na kupotoka kwa kiwango cha inchi 2.8.

1. Nini maana urefu wa mlango utaruhusu 95% ya wanaume kuingia ndege bila bending?
2. Kudhani kwamba nusu ya abiria 200 ni wanaume. Nini maana urefu wa mlango hutimiza hali ya kuwa kuna uwezekano wa 0.95 kwamba urefu huu ni mkubwa kuliko urefu wa wastani wa wanaume 100?
3. Kwa wahandisi kubuni 757, ambayo matokeo ni muhimu zaidi: urefu kutoka sehemu a au sehemu b? Kwa nini?

Jibu

1. Tunajua kwamba\(\mu_{x} = \mu = 69\) na tuna\(\sigma_{x} = 2.8\). Urefu wa mlango unapatikana kuwa katika Norm\((0.95,69,2.8) = 73.61\)
2. Tunajua kwamba\(\mu_{x} = \mu = 69\) na tuna\(\sigma_{x} = 2.8\). Hivyo, katika kawaida\((0.95,69,0.28) = 69.49\)
3. Wakati wa kubuni urefu wa mlango, tunahitaji kuingiza tofauti iwezekanavyo ili kuhudumia abiria wengi iwezekanavyo. Kwa hiyo, tunahitaji kutumia matokeo kulingana na sehemu a.

Historia Kumbuka: Kawaida makadirio ya Binomial

Kihistoria, kuwa na uwezo wa kukokotoa probabilities ya binomial ilikuwa mojawapo ya maombi muhimu zaidi ya theorem ya kikomo ya kati. Probabilities ya Binomial yenye thamani ndogo kwa\(n\) (sema, 20) yalionyeshwa kwenye meza katika kitabu. Ili kuhesabu uwezekano na maadili makubwa ya\(n\), ulibidi kutumia formula ya binomial, ambayo inaweza kuwa ngumu sana. Kwa kutumia makadirio ya kawaida kwa usambazaji binomial kilichorahisishwa mchakato. Kukokotoa makadirio ya kawaida kwa usambazaji binomial, kuchukua rahisi random sampuli kutoka idadi ya watu. Lazima kufikia masharti ya usambazaji wa binomial:

• kuna idadi fulani ya majaribio\(n\) ya kujitegemea
• matokeo ya jaribio lolote ni mafanikio au kushindwa
• kila kesi ina uwezekano huo wa mafanikio\(p\)

Kumbuka kwamba ikiwa\(X\) ni variable ya binomial random, basi\(X \sim B(n, p)\). Sura ya usambazaji wa binomial inahitaji kuwa sawa na sura ya usambazaji wa kawaida. Ili kuhakikisha hili, kiasi\(np\) na\(nq\) lazima wote kuwa zaidi ya tano (\(np > 5\)na\(nq > 5\)); makadirio ni bora kama wote wawili ni kubwa kuliko au sawa na 10). Kisha binomial inaweza kuhesabiwa na usambazaji wa kawaida na kupotoka kwa maana\(\mu = np\) na kiwango\(\sigma = \sqrt{npq}\). Kumbuka hilo\(q = 1 - p\). Ili kupata makadirio bora, ongeza 0.5\(x\) au uondoe 0.5 kutoka\(x\) (kutumia\(x + 0.5\) au\(x - 0.5\)). Nambari 0.5 inaitwa sababu ya kusahihisha mwendelezo na hutumiwa katika mfano unaofuata.

Mfano\(\PageIndex{5}\)

Tuseme katika shule ya chekechea ^ya ndani kupitia wilaya ya shule ya 12 (K - 12), asilimia 53 ya idadi ya watu wanapendelea shule ya mkataba kwa darasa K hadi 5. Sampuli rahisi ya random ya 300 inachunguzwa.

1. Kupata uwezekano kwamba angalau 150 neema mkataba shule.
2. Kupata uwezekano kwamba katika zaidi 160 neema mkataba shule.
3. Kupata uwezekano kwamba zaidi ya 155 neema shule mkataba.
4. Kupata uwezekano kwamba chini ya 147 neema mkataba shule.
5. Kupata uwezekano kwamba hasa 175 neema mkataba shule.

Hebu nambari\(X =\) inayopendeza shule ya mkataba kwa ajili ya darasa K kupitia nyimbo 5. \(X \sim B(n, p)\)wapi\(n = 300\) na\(p = 0.53\). Tangu\(np > 5\) na\(nq > 5\), kutumia makadirio ya kawaida ya binomial. Njia za kupotoka kwa maana na kiwango ni\(\mu = np\) na\(\sigma = \sqrt{npq}\). Maana ni 159 na kupotoka kwa kawaida ni 8.6447. kutofautiana random kwa usambazaji wa kawaida ni\(X\). \(Y \sim N(159, 8.6447)\). Angalia Distribution Normal kwa msaada na maelekezo calculator.

Kwa sehemu a, wewe ni pamoja na 150 hivyo\(P(X \geq 150)\) ina makadirio ya kawaida\(P(Y \geq 149.5) = 0.8641\).

kawaidacf\((149.5,10^{99},159,8.6447) = 0.8641\).

Kwa sehemu b, wewe ni pamoja na 160 hivyo\(P(X \leq 160)\) ina makadirio ya kawaida\(P(Y \leq 160.5) = 0.5689\).

kawaidacf\((0,160.5,159,8.6447) = 0.5689\)

Kwa sehemu c, wewe kuwatenga 155 hivyo\(P(X > 155)\) ina makadirio ya kawaida\(P(y > 155.5) = 0.6572\).

kawaidacf\((155.5,10^{99},159,8.6447) = 0.6572\).

Kwa sehemu d, wewe kuwatenga 147 hivyo\(P(X < 147)\) ina makadirio ya kawaida\(P(Y < 146.5) = 0.0741\).

kawaidacf\((0,146.5,159,8.6447) = 0.0741\)

Kwa sehemu e,\(P(X = 175)\) ina makadirio ya kawaida\(P(174.5 < Y < 175.5) = 0.0083\).

kawaidacf\((174.5,175.5,159,8.6447) = 0.0083\)

Kwa sababu ya calculators na programu ya kompyuta kwamba basi wewe mahesabu probabilities binomial kwa maadili kubwa ya\(n\) urahisi, si lazima kutumia makadirio ya kawaida kwa usambazaji binomial, mradi una upatikanaji wa zana hizi teknolojia. Maabara mengi ya shule yana Microsoft Excel, mfano wa programu ya kompyuta ambayo huhesabu uwezekano wa binomial. Wanafunzi wengi wanapata mahesabu ya mfululizo wa TI-83 au 84, na huhesabu kwa urahisi uwezekano wa usambazaji wa binomial. Ikiwa unapiga “hesabu ya usambazaji wa uwezekano wa binomial” kwenye kivinjari cha wavuti, unaweza kupata angalau calculator moja ya mtandaoni kwa binomial.

Kwa mfano, probabilities ni mahesabu kwa kutumia usambazaji zifuatazo binomial: (\(n = 300 and p = 0.53\)). Linganisha majibu ya usambazaji wa binomial na ya kawaida. Angalia Discrete Random Vigezo kwa msaada na maelekezo calculator kwa binomial.

\(P(X \geq 150)\): 1 - binomialcdf\((300,0.53,149) = 0.8641\)

\(P(X \leq 160)\): binomialcdf\((300,0.53,160) = 0.5684\)

\(P(X > 155)\): 1 - binomialcdf\((300,0.53,155) = 0.6576\)

\(P(X < 147)\): binomialcdf\((300,0.53,146) = 0.0742\)

\(P(X = 175)\):( Unatumia pdf ya binomial.) binomial pdf\((300,0.53,175) = 0.0083\)

Zoezi\(\PageIndex{5}\)

Katika mji, 46 asilimia ya idadi ya watu neema madarakani, Dawn Morgan, kwa meya. Sampuli rahisi ya random ya 500 inachukuliwa. Kwa kutumia mwendelezo marekebisho sababu, kupata uwezekano kwamba angalau 250 neema Dawn Morgan kwa meya.

Jibu

0.0401

Marejeo

• Takwimu kutoka Wall Street Journal.
• “Utafiti wa Taifa wa Afya na Lishe.” Kituo cha Kudhibiti Magonjwa na Kuzuia. Inapatikana mtandaoni kwenye http://www.cdc.gov/nchs/nhanes.htm (imefikia Mei 17, 2013).

faharasa

Usambazaji wa kielelezo

kuendelea random variable (RV) kwamba inaonekana wakati sisi ni nia ya vipindi vya muda kati ya baadhi ya matukio random, kwa mfano, urefu wa muda kati ya waliofika dharura katika hospitali, nukuu:\(X \sim Exp(m)\). Maana ni\(\mu = \dfrac{1}{m}\) na kupotoka kwa kiwango ni\(\sigma = \dfrac{1}{m}\). uwezekano wiani kazi ni\(f(x) = me^{-mx}\),\(x \geq 0\) na nyongeza usambazaji kazi ni\(P(X \leq x) = 1 - e^{-mx}\).

Maana

idadi ambayo hatua tabia ya kati; jina la kawaida kwa maana ni “wastani.” Neno “maana” ni fomu iliyofupishwa ya “maana ya hesabu.” Kwa ufafanuzi, maana ya sampuli (iliyoonyeshwa na\(\bar{x}\)) ni\(\bar{x} = \dfrac{\text{Sum of all values in the sample}}{\text{Number of values in the sample}}\), na maana ya idadi ya watu (iliyoonyeshwa na\(\mu\)) ni\(\mu = \dfrac{\text{Sum of all values in the population}}{\text{Number of values in the population}}\).

Usambazaji wa kawaida

kuendelea random variable (RV) na pdf\(f(x) = \dfrac{1}{\sigma \sqrt{2\pi}}e^{\dfrac{(x - \mu)^{2}}{2\sigma^{2}}}\), ambapo\(\mu\) ni maana ya usambazaji na\(\sigma\) ni kupotoka kiwango.; nukuu:\(X \sim N(\mu, \sigma)\). Ikiwa\(\mu = 0\) na\(\sigma = 1\), RV inaitwa usambazaji wa kawaida wa kawaida.

Usambazaji Sare

kuendelea random variable (RV) ambayo ina matokeo sawa uwezekano juu ya uwanja,\(a < x < b\); mara nyingi hujulikana kama Distribution Rectangular kwa sababu graph ya pdf ina aina ya mstatili. Nukuu:\(X \sim U(a, b)\). Maana ni\(\mu = \dfrac{a+b}{2}\) na kupotoka kwa kiwango ni\(\sigma = \sqrt{\dfrac{(b-a)^{2}}{12}}\). Kazi ya wiani ya uwezekano ni\(f(x) = \dfrac{a+b}{2}\) kwa\(a < x < b\) au\(a \leq x \leq b\). Usambazaji wa jumla ni\(P(X \leq x) = \dfrac{x-a}{b-a}\).