Sura ya 10 Mazoezi Mapitio
- Page ID
- 177508
Sura ya 10 Mazoezi Mapitio
10.1 Kutatua Equations Quadratic Kutumia Mizizi ya Mizizi ya Mraba
Katika mazoezi yafuatayo, tatua kutumia Mizizi ya Mizizi ya Mraba.
\(x^2=100\)
- Jibu
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- Jibu
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- Jibu
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- Jibu
-
hakuna suluhisho
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- Jibu
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- Jibu
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
Katika mazoezi yafuatayo, tatua kutumia Mizizi ya Mizizi ya Mraba.
\((p−5)^2+3=19\)
- Jibu
-
p=1, 9
\((q+4)^2=9\)
\((u+1)^2=45\)
- Jibu
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- Jibu
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- Jibu
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- Jibu
-
hakuna suluhisho
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- Jibu
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- Jibu
-
a=-32, 34
\(4b^2−28b+49=25\)
10.2 Kutatua Equations Quadratic Kutumia Kukamilisha Square
Katika mazoezi yafuatayo, jaza mraba ili kufanya trinomial kamili ya mraba. Kisha kuandika matokeo kama mraba wa binomial.
\(x^2+22x\)
- Jibu
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- Jibu
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- Jibu
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- Jibu
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
Katika mazoezi yafuatayo, tatua kwa kukamilisha mraba.
\(c^2+20c=21\)
- Jibu
-
c=1, -21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- Jibu
-
x=-4, 8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- Jibu
-
hakuna suluhisho
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- Jibu
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- Jibu
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- Jibu
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- Jibu
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- Jibu
-
p=0, 6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- Jibu
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- Jibu
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 Tatua Ulinganisho wa Quadratic Kutumia Mfumo wa Quadratic
Katika mazoezi yafuatayo, tatua kwa kutumia Mfumo wa Quadratic.
\(4x^2−5x+1=0\)
- Jibu
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- Jibu
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- Jibu
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- Jibu
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- Jibu
-
hakuna ufumbuzi halisi
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- Jibu
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- Jibu
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- Jibu
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
Katika mazoezi yafuatayo, tambua idadi ya ufumbuzi kwa kila equation ya quadratic.
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- Jibu
-
- 1
- 2
- 2
- hakuna
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
Katika mazoezi yafuatayo, kutambua njia sahihi zaidi (Factoring, Square Root, au Quadratic Formula) kutumia kutatua kila equation quadratic.
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- Jibu
-
- sababu
- Mfumo wa Quadratic
- mizizi ya mraba
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 Kutatua Maombi Inatokana na Equations Quadratic
Katika mazoezi yafuatayo, tatua kwa kutumia mbinu za kuzingatia, kanuni ya mizizi ya mraba, au formula ya quadratic.
Kupata mbili mfululizo idadi isiyo ya kawaida ambayo bidhaa ni 323.
- Jibu
-
Nambari mbili za mfululizo zisizo za kawaida ambazo bidhaa zake ni 323 ni 17 na 19, na -17 na 19-19.
Pata namba mbili za mfululizo ambazo bidhaa zake ni 624.
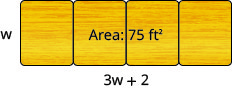
Bendera ya triangular ina eneo la sentimita za mraba 351. Urefu wa msingi ni sentimita mbili zaidi ya mara nne urefu. Pata urefu na urefu wa msingi.
- Jibu
-
Urefu wa bendera ni 13 cm na urefu wa upande ni 54 cm.
Julius alijenga kesi ya kuonyesha triangular kwa ukusanyaji wake wa sarafu. Urefu wa kesi ya kuonyesha ni inchi sita chini ya mara mbili upana wa msingi. Eneo la nyuma ya kesi ni inchi za mraba 70. Pata urefu na upana wa kesi hiyo.
Mosaic ya tile katika sura ya pembetatu sahihi hutumiwa kama kona ya njia ya mstatili. Hypotenuse ya mosaic ni miguu 5. Sehemu moja ya mosaic ni mara mbili kwa muda mrefu kama upande mwingine. Urefu wa pande ni nini? Pande zote hadi kumi ya karibu.

- Jibu
-
Urefu wa pande za mosaic ni 2.2 na 4.4 miguu.
Kipande cha mstatili cha plywood kina diagonal, ambayo inachukua miguu miwili zaidi ya upana. Urefu wa plywood ni mara mbili upana. Urefu wa diagonal ya plywood ni nini? Pande zote hadi kumi ya karibu.
Kutembea mbele kutoka mitaani hadi nyumba ya Pam kuna eneo la futi za mraba 250. Urefu wake ni mbili chini ya mara nne upana wake. Pata urefu na upana wa barabara ya barabara. Pande zote hadi kumi ya karibu.
- Jibu
-
Upana wa kutembea mbele ni futi 8.1 na urefu wake ni futi 30.8.
Kwa chama cha kuhitimu cha Sophia, meza kadhaa za upana huo zitapangwa mwisho hadi mwisho ili kutoa meza ya kutumikia na eneo la jumla la miguu ya mraba 75. Urefu wa jumla wa meza utakuwa mbili zaidi ya mara tatu upana. Pata urefu na upana wa meza ya kutumikia ili Sophia anaweza kununua kitambaa cha ukubwa sahihi. Jibu la pande zote kwa kumi ya karibu.
Mpira unatupwa kwa wima hewa na kasi ya 160 ft/sec. Kutumia formula\(h=−16t^2+v_{0}t\) kuamua wakati mpira itakuwa 384 miguu kutoka ardhini. Pande zote hadi kumi ya karibu.
- Jibu
-
Mpira utafikia miguu 384 njiani juu katika sekunde 4 na njiani chini katika sekunde 6.
Risasi inafukuzwa moja kwa moja kutoka ardhini kwa kasi ya 320 ft/sec. Kutumia\(h=−16t^2+v_{0}t\) formula kuamua wakati risasi kufikia miguu 800. Pande zote hadi kumi ya karibu.
10.5 Graphing Quadratic equations katika Vigezo viwili
Katika mazoezi yafuatayo, grafu kwa hatua ya kupanga.
Grafu\(y=x^2−2\)
- Jibu
-
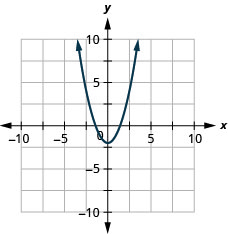
Grafu\(y=−x^2+3\)
Katika mazoezi yafuatayo, onyesha kama parabolas zifuatazo zinafungua au chini.
\(y=−3x^2+3x−1\)
- Jibu
-
chini
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- Jibu
-
juu
A\(y=−4x^2−7x+1\)
Katika mazoezi yafuatayo, tafuta
- mhimili wa ulinganifu na,
- kipeo.
\(y=−x^2+6x+8\)
- Jibu
-
- x=3
- (3,17)
\(y=2x^2−8x+1\)
Katika mazoezi yafuatayo, tafuta x - na y -intercepts.
\(y=x^2−4x+5\)
- Jibu
-
y: (0,5); x: (5,0), (-1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- Jibu
-
y: (0,10); x: hakuna
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- Jibu
-
y: (0,1); x: (14,0)
\(y=x^2+16x+64\)
Katika mazoezi yafuatayo, grafu kwa kutumia intercepts, vertex, na mhimili wa ulinganifu.
\(y=x^2+8x+15\)
- Jibu
-
y: (0,15); x: (-3,0), (-5,0);
mhimili: x = -4; kipeo :( -4, -1)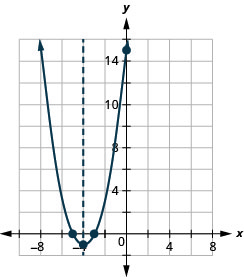
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- Jibu
-
y: (0, -16); x: (4,0);
mhimili: x=4; kipeo :( 4,0)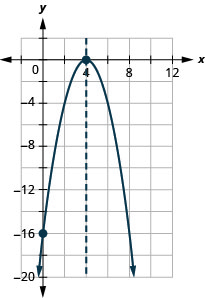
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- Jibu
-
y: (0,13); x:hakuna;
mhimili: x=—3; kipeo :( -3,4)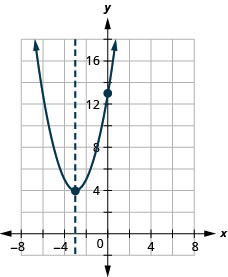
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- Jibu
-
y: (0, -11); x: (3.1,0), (0.9,0);
mhimili: x=2; kipeo :( 2,5)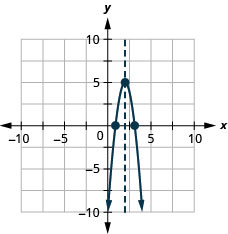
\(y=x^2+8x+10\)
Katika mazoezi yafuatayo, pata thamani ya chini au ya juu.
\(y=7x^2+14x+6\)
- Jibu
-
Thamani ya chini ni -1 wakati\(x=−1\).
\(y=−3x^2+12x−10\)
Katika mazoezi yafuatayo, tatua. Rounding majibu ya kumi karibu.
Mpira unatupwa juu kutoka chini na kasi ya awali ya 112 ft/sec. Matumizi equation quadratic\(h=−16t^2+112t\) kupata muda gani itachukua mpira kufikia urefu upeo, na kisha kupata urefu upeo.
- Jibu
-
Katika sekunde 3.5 mpira uko kwenye urefu wake wa juu wa futi 196.
Kituo cha huduma za mchana kinafunga eneo la mstatili upande wa jengo lao ili watoto kucheza nje. Wanahitaji kuongeza eneo hilo kwa kutumia miguu 180 ya uzio kwenye pande tatu za yadi. Equation quadratic\(A=−2x^2+180x\) inatoa eneo, A, ya yadi kwa urefu, x, ya jengo ambalo litapakana na yadi. Pata urefu wa jengo ambalo linapaswa kupakana na yadi ili kuongeza eneo hilo, na kisha upate eneo la juu.
Mazoezi mtihani
Tumia Mizizi ya Mizizi ya Mraba ili kutatua equation ya quadratic:\(3(w+5)^2=27\).
- Jibu
-
w=,12, -8
Tumia Kukamilisha Square kutatua equation quadratic:\(a^2−8a+7=23\)
Tumia Mfumo wa Quadratic kutatua equation ya quadratic:\(2m^2−5m+3=0\).
- Jibu
-
m=1, 32
Tatua usawa wa quadratic zifuatazo. Tumia njia yoyote.
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- Jibu
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- Jibu
-
hakuna ufumbuzi halisi
\(\frac{4}{3}y^2−4y+3=0\)
Tumia ubaguzi kuamua idadi ya ufumbuzi wa kila equation ya quadratic.
\(6p^2−13p+7=0\)
- Jibu
-
2
\(3q^2−10q+12=0\)
Tatua kwa kuzingatia, Mali ya Mizizi ya Mraba, au Mfumo wa Quadratic.
Pata namba mbili za mfululizo ambazo bidhaa zake ni 360.
- Jibu
-
Nambari mbili za mfululizo hata ni -20 na 18-18 na 18 na 20.
Urefu wa diagonal ya mstatili ni tatu zaidi ya upana. Urefu wa mstatili ni mara tatu upana. Pata urefu wa diagonal. (Pande zote hadi kumi ya karibu.)
Kwa kila parabola, tafuta
- njia ambayo inafungua,
- mhimili wa ulinganifu,
- kipeo,
- x - na y -intercepts, na
- thamani ya kiwango cha juu au cha chini.
\(y=3x^2+6x+8\)
- Jibu
-
- juu
- \(x=−1\)
- (-1,5)
- y: (0,8); x: hakuna; (0,8)
- kima cha chini cha thamani ya 5 wakati\(x=−1\).
\(y=x^2−4\)
\(y=x^2+10x+24\)
- Jibu
-
- juu
- \(x=−5\)
- (-5, -1)
- y: (0,24); x: (-6,0), (-4,0)
- thamani ya chini ya -5 wakati\(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- Jibu
-
- chini
- \(x=−4\)
- (-4,32)
- y; (0,16); x: (-9.7,0), (1.7,0)
- thamani ya juu ya 32 wakati\(x=−4\)
Grafu parabolas zifuatazo kwa kutumia intercepts, vertex, na mhimili wa ulinganifu.
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- Jibu
-
y: (0,9); x: (-34,0)
mhimili:\( x=−\frac{3}{4}\); vertex:\((−\frac{3}{4},0)\)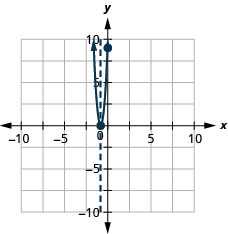
Kutatua.
Puto ya maji imezinduliwa juu kwa kiwango cha 86 ft/sec. Kutumia formula h=-16t ^ 2+86t, tafuta muda gani itachukua puto kufikia urefu wa juu na kisha kupata urefu wa juu. Pande zote hadi kumi ya karibu.