9.6: Tatua equations na Mizizi ya Mraba
- Page ID
- 177404
Mwishoni mwa sehemu hii, utaweza:
- Kutatua equations radical
- Tumia mizizi ya mraba katika programu
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kurahisisha: ⓐ\(\sqrt{9}\) ⓑ\(9^2\).
Kama amekosa tatizo hili, mapitio Mfano 9.1.1 na Zoezi 1.3.22. - Tatua: 5 (x+1) -4=3 (2x-7).
Kama amekosa tatizo hili, kupitia Zoezi 2.4.16. - Kutatua:\(n^2−6n+8=0\).
Kama amekosa tatizo hili, kupitia Zoezi 7.6.13.
Kutatua equations radical
Katika sehemu hii tutaweza kutatua equations ambayo ina variable katika radicand ya mizizi ya mraba. Ulinganisho wa aina hii huitwa equations radical.
Equation ambayo variable iko katika radicand ya mizizi ya mraba inaitwa equation radical.
Kama kawaida, katika kutatua milinganyo haya, tunachofanya kwa upande mmoja wa equation ni lazima tufanye kwa upande mwingine pia. Kwa kuwa squaring wingi na kuchukua mizizi mraba ni 'kinyume' shughuli, sisi mraba pande zote mbili ili kuondoa ishara radical na kutatua kwa variable ndani.
Lakini kumbuka kwamba tunapoandika\(\sqrt{a}\) tunamaanisha mizizi kuu ya mraba. Hivyo\(\sqrt{a} \ge 0\) daima. Wakati sisi kutatua equations radical kwa squaring pande zote mbili tunaweza kupata ufumbuzi algebraic ambayo kufanya\(\sqrt{a}\) hasi. Suluhisho hili la algebraic haliwezi kuwa suluhisho la equation ya awali ya radical; ni suluhisho la nje. Tuliona ufumbuzi wa nje wakati tulipotatua usawa wa busara, pia.
Kwa equation\(\sqrt{x+2}=x\):
- Je, x=2 ni suluhisho?
- Je, x=-1 ni suluhisho?
- Jibu
-
1. Je, x=2 ni suluhisho?
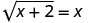
Hebu x = 2. 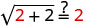
Kurahisisha. 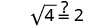
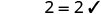
2 ni suluhisho. 2. Je, x=-1 ni suluhisho?
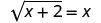
Hebu x = -1. 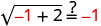
Kurahisisha. 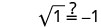
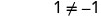
-1 si suluhisho. -1 ni suluhisho la nje kwa equation.
Kwa equation\(\sqrt{x+6}=x\):
- Je, x=-2 ni suluhisho?
- Je, x=3 ni suluhisho?
- Jibu
-
- hapana
- ndiyo
Kwa equation\(\sqrt{−x+2}=x\):
- Je, x=-2 ni suluhisho?
- Je, x=1 ni suluhisho?
- Jibu
-
- hapana
- ndiyo
Kwa\(a \ge 0\),\((\sqrt{a})^2=a\)
Jinsi ya kutatua equations Radical
Kutatua:\(\sqrt{2x−1}=7\)
- Jibu
-
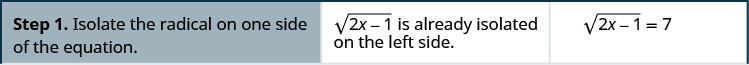



Kutatua:\(\sqrt{3x−5}=5\).
- Jibu
-
10
Kutatua:\(\sqrt{4x+8}=6\).
- Jibu
-
7
- Isulate radical upande mmoja wa equation.
- Square pande zote mbili za equation.
- Kutatua equation mpya.
- Angalia jibu.
Kutatua:\(\sqrt{5n−4}−9=0\).
- Jibu
-
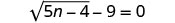
Ili kutenganisha radical, ongeza 9 kwa pande zote mbili. 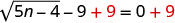
Kurahisisha. 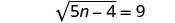
Square pande zote mbili za equation. 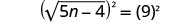
Kutatua equation mpya. 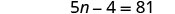


Angalia jibu.

Suluhisho ni n = 17.
Kutatua:\(\sqrt{3m+2}−5=0\).
- Jibu
-
\(\frac{23}{3}\)
Kutatua:\(\sqrt{10z+1}−2=0\).
- Jibu
-
\(\frac{3}{10}\)
Kutatua:\(\sqrt{3y+5}+2=5\).
- Jibu
-
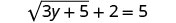
Ili kutenganisha radical, toa 2 kutoka pande zote mbili. 
Kurahisisha. 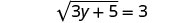
Square pande zote mbili za equation. 
Kutatua equation mpya. 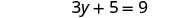

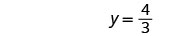
Angalia jibu.
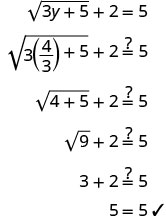
Suluhisho ni\(y=\frac{4}{3}\)
Kutatua:\(\sqrt{3p+3}+3=5\).
- Jibu
-
\(\frac{1}{3}\)
Kutatua:\(\sqrt{5q+1}+4=6\).
- Jibu
-
\(\frac{3}{5}\)
Tunapotumia ishara kali, tunamaanisha mizizi kuu au chanya. Kama equation ina mizizi mraba sawa na idadi hasi, equation kwamba haitakuwa na ufumbuzi.
Kutatua:\(\sqrt{9k−2}+1=0\).
- Jibu
-
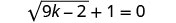
Ili kutenganisha radical, toa 1 kutoka pande zote mbili. 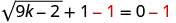
Kurahisisha. 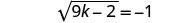
Kwa kuwa mizizi ya mraba ni sawa na idadi hasi, equation haina suluhisho.
Kutatua:\(\sqrt{2r−3}+5=0\)
- Jibu
-
hakuna suluhisho
Kutatua:\(\sqrt{7s−3}+2=0\).
- Jibu
-
hakuna suluhisho
\[\begin{array}{cc} {(a+b)^2=a^2+2ab+b^2}&{(a−b)^2=a^2−2ab+b^2}\\ \nonumber \end{array}\]
Usisahau muda wa kati!
Kutatua:\(\sqrt{p−1}+1=p\).
- Jibu
-
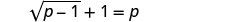
Ili kutenganisha radical, toa 1 kutoka pande zote mbili. 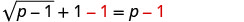
Kurahisisha. 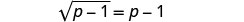
Square pande zote mbili za equation. 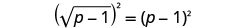
Kurahisisha, kisha kutatua equation mpya. 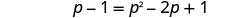
Ni equation quadratic, hivyo kupata sifuri upande mmoja. 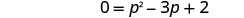
Fanya upande wa kulia. 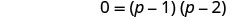
Tumia mali ya bidhaa ya sifuri. 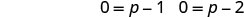
Kutatua kila equation. 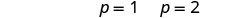
Angalia majibu.
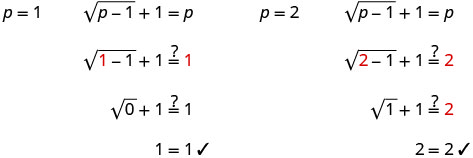
Ufumbuzi ni p = 1, p = 2.
Kutatua:\(\sqrt{x−2}+2=x\).
- Jibu
-
2, 3
Kutatua:\(\sqrt{y−5}+5=y\).
- Jibu
-
5, 6
Kutatua:\(\sqrt{r+4}−r+2=0\).
- Jibu
-
\(\sqrt{r+4}−r+2=0\) Isulate radical. \(\sqrt{r+4}=r−2\) Square pande zote mbili za equation. \((\sqrt{r+4})^2=(r−2)^2\) Kutatua equation mpya. \(r+4=r^2−4r+4\) Ni equation quadratic, hivyo kupata sifuri upande mmoja. \(0=r^2−5r\) Fanya upande wa kulia. \(0=r(r−5)\) Tumia mali ya bidhaa ya sifuri. 0=r 0=r-5 Kutatua equation. r=0 r=5 Angalia jibu.
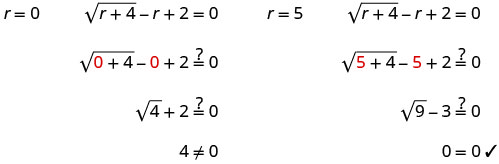
r=5 r=0 ni suluhisho la nje.
Kutatua:\(\sqrt{m+9}−m+3=0\).
- Jibu
-
7
Kutatua:\(\sqrt{n+1}−n+1=0\)
- Jibu
-
3
Wakati kuna mgawo mbele ya radical, lazima tuifanye mraba, pia.
Kutatua:\(3\sqrt{3x−5}−8=4\).
- Jibu
-
\(3\sqrt{3x−5}−8=4\) Isulate radical. \(3\sqrt{3x−5}=12\) Square pande zote mbili za equation. \((3\sqrt{3x−5})^2=(12)^2\) Kurahisisha, kisha kutatua equation mpya. 9 (3x-5) =144 Kusambaza. 27x-45=144 Kutatua equation. 27x=189 x=7 Angalia jibu.
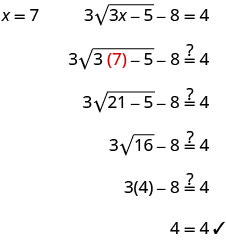
Suluhisho ni x=7.
Kutatua:\(\sqrt{24a+2}−16=16\).
- Jibu
-
\(\frac{127}{2}\)
Kutatua:\(\sqrt{36b+3}−25=50\).
- Jibu
-
\(\frac{311}{3}\)
Kutatua:\(\sqrt{4z−3}=\sqrt{3z+2}\).
- Jibu
-
\(\sqrt{4z−3}=\sqrt{3z+2}\) Maneno makubwa yanatengwa \(\sqrt{4z−3}=\sqrt{3z+2}\) Square pande zote mbili za equation. \((\sqrt{4z−3})^2=(\sqrt{3z+2})^2\) Kurahisisha, kisha kutatua equation mpya 4z-3=3z+2 z-3=2 z=5 x=7 Angalia jibu.
Tunakuacha ili kuonyesha kwamba hundi za 5!
Suluhisho ni z=5.
Kutatua:\(\sqrt{2x−5}=\sqrt{5x+3}\).
- Jibu
-
hakuna suluhisho
Kutatua:\(\sqrt{7y+1}=\sqrt{2y−5}\).
- Jibu
-
hakuna suluhisho
Wakati mwingine baada ya mraba pande zote mbili za equation, bado tuna variable ndani radical. Wakati huo hutokea, tunarudia Hatua ya 1 na Hatua ya 2 ya utaratibu wetu. Sisi kutenganisha radical na mraba pande zote mbili za equation tena.
Kutatua:\(\sqrt{m}+1=\sqrt{m+9}\).
- Jibu
-
\(\sqrt{m}+1=\sqrt{m+9}\) Radical upande wa kulia ni pekee.
Mraba pande zote mbili
\((\sqrt{m}+1)^2=(\sqrt{m+9})^2\) Kurahisisha - kuwa makini sana kama wewe kuzidisha! \(m+2\sqrt{m}+1=m+9\) Bado kuna radical katika equation.
Kwa hiyo tunapaswa kurudia hatua zilizopita. Isulate radical.
\(2\sqrt{m}=8\) Square pande zote mbili. \((2\sqrt{m})^2=(8)^2\) Kurahisisha, kisha kutatua equation mpya. 4m=64 m=16 Angalia jibu.
Sisi kuondoka ni kwa wewe kuonyesha kwamba m = 16 hundi!
Suluhisho ni m=16.
Kutatua:\(\sqrt{x}+3=\sqrt{x+5}\).
- Jibu
-
hakuna suluhisho
Kutatua:\(\sqrt{m}+5=\sqrt{m+16}\).
- Jibu
-
hakuna suluhisho
Kutatua:\(\sqrt{q−2}+3=\sqrt{4q+1}\).
- Jibu
-
\(\sqrt{q−2}+3=\sqrt{4q+1}\) Radical upande wa kulia ni pekee.
Mraba pande zote mbili
\((\sqrt{q−2}+3)^2=(\sqrt{4q+1})^2\) Kurahisisha. \(q−2+6\sqrt{q−2}+9=4q+1\) Bado kuna radical katika equation.
Kwa hiyo tunapaswa kurudia hatua zilizopita. Isulate radical.
\(6\sqrt{q−2}=3q−6\) Square pande zote mbili. \((6\sqrt{q−2})^2=(3q−6)^2\) Kurahisisha, kisha kutatua equation mpya. \(36(q−2)=9q^2−36q+36\) Kusambaza. \(36q−72=9q^2−36q+36\) Ni equation quadratic, hivyo kupata sifuri upande mmoja. \(0=9q^2−72q+108\) Fanya upande wa kulia. \(0=9(q^2−8q+12)\)
\(0=9(q−6)(q−2)\)
Tumia mali ya bidhaa zero \[\begin{array}{ll} {q−6=0}&{q−2=0}\\ {q=6}&{q=2}\\ \nonumber \end{array}\] Hundi zimeachwa kwako. (Ufumbuzi wote wanapaswa kufanya kazi.)
Ufumbuzi ni q=6 na q=2.
Kutatua:\(\sqrt{y−3}+2=\sqrt{4y+2}\).
- Jibu
-
hakuna suluhisho
Kutatua:\(\sqrt{n−4}+5=\sqrt{3n+3}\).
- Jibu
-
hakuna suluhisho
Tumia Mizizi ya Mraba katika Maombi
Unapoendelea kupitia kozi zako za chuo, utakutana na fomu ambazo zinajumuisha mizizi ya mraba katika taaluma nyingi. Tayari tumetumia formula kutatua maombi ya jiometri.
Tutatumia Mkakati wetu wa Kutatua Tatizo kwa Maombi ya Jiometri, na marekebisho kidogo, kutupa mpango wa kutatua maombi na fomu kutoka kwa nidhamu yoyote.
- Soma tatizo na uhakikishe maneno yote na mawazo yanaeleweka. Ikiwa inafaa, futa takwimu na uifanye alama kwa habari iliyotolewa.
- Tambua kile tunachotafuta.
- Jina kile tunachotafuta kwa kuchagua variable kuwakilisha.
- Tafsiri katika equation kwa kuandika formula sahihi au mfano kwa hali hiyo. Mbadala katika taarifa iliyotolewa.
- Kutatua equation kutumia mbinu nzuri algebra.
- Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
- Jibu swali kwa sentensi kamili.
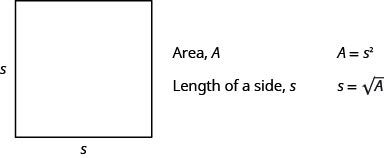
Tulitumia formula A=L · W ili kupata eneo la mstatili na urefu L na upana W. Mraba ni mstatili ambao urefu na upana ni sawa. Kama sisi basi s kuwa urefu wa upande wa mraba, eneo la mraba ni\(s^2\).
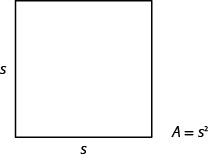
Fomu\(A=s^2\) inatupa eneo la mraba ikiwa tunajua urefu wa upande. Nini kama tunataka kupata urefu wa upande kwa eneo fulani? Kisha tunahitaji kutatua equation kwa s.
\[\begin{array}{ll} {}&{A=s^2}\\ {\text{Take the square root of both sides.}}&{\sqrt{A}=\sqrt{s^2}}\\ {\text{Simplify.}}&{s=\sqrt{A}}\\ \nonumber \end{array}\]
Tunaweza kutumia formula\(s=\sqrt{A}\) ili kupata urefu wa upande wa mraba kwa eneo lililopewa.
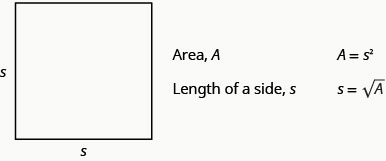
Tutaonyesha mfano wa hili katika mfano unaofuata.
Mike na Lychelle wanataka kufanya patio mraba. Wana saruji ya kutosha kusafisha eneo la futi za mraba 200. Tumia formula\(s=\sqrt{A}\) ili kupata urefu wa kila upande wa patio. Pindua jibu lako kwa sehemu ya kumi ya mguu.
- Jibu
-
Hatua ya 1. Soma tatizo. Chora takwimu na
uifanye alama kwa habari iliyotolewa.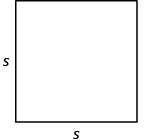
A = 200 mraba miguu Hatua ya 2. Tambua unachotafuta. Urefu wa upande wa patio ya mraba. Hatua ya 3. Jina unachotafuta kwa
kuchagua variable kuwakilisha.Hebu s = urefu wa upande. Hatua ya 4. Tafsiri katika equation kwa kuandika formula
sahihi au mfano kwa hali hiyo.
Badilisha taarifa iliyotolewa.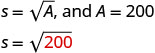
Hatua ya 5. Kutatua equation kutumia
mbinu nzuri algebra. Pande zote kwa sehemu moja ya decimal.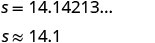
Hatua ya 6. Angalia jibu katika tatizo na
uhakikishe kuwa ni busara.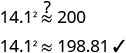
Hii ni karibu kutosha kwa sababu tulizunguka mizizi ya
mraba.
Je patio na upande 14.1 miguu busara?
Ndiyo.Hatua ya 7. Jibu swali kwa
sentensi kamili.Kila upande wa patio lazima iwe miguu 14.1.
Katie anataka kupanda lawn mraba katika yadi yake ya mbele. Ana sod ya kutosha kufunika eneo la futi za mraba 370. Kutumia formula\(s=\sqrt{A}\) kupata urefu wa kila upande wa lawn yake. Pindua jibu lako kwa sehemu ya kumi ya mguu.
- Jibu
-
Futi 19.2
Sergio anataka kufanya mosaic mraba kama inlay kwa meza yeye ni kujenga. Ana tile ya kutosha kufunika eneo la sentimita za mraba 2704. Tumia formula\(s=\sqrt{A}\) ili kupata urefu wa kila upande wa mosaic yake. Pindua jibu lako kwa sehemu ya kumi ya mguu.
- Jibu
-
52.0 cm
Matumizi mengine ya mizizi ya mraba inahusiana na mvuto.
Kwenye Dunia, ikiwa kitu kimeshuka kutoka urefu wa miguu ya hh, wakati katika sekunde itachukua kufikia ardhi hupatikana kwa kutumia formula,
\(t=\frac{\sqrt{h}}{4}\)
Kwa mfano, kama kitu ni imeshuka kutoka urefu wa miguu 64, tunaweza kupata muda inachukua kufikia ardhi kwa kubadilisha h = 64 katika formula.
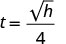 |
|
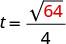 |
|
| Chukua mizizi ya mraba ya 64. | 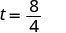 |
| Kurahisisha sehemu. | 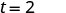 |
Itachukua sekunde 2 kwa kitu kilichoshuka kutoka kimo cha futi 64 kufikia ardhi.
Christy imeshuka miwani yake kutoka daraja 400 miguu juu ya mto. Kutumia formula ya\(t=\frac{\sqrt{h}}{4}\) kupata sekunde ngapi ilichukua kwa ajili ya miwani ya kufikia mto.
- Jibu
-
Hatua ya 1. Soma tatizo. Hatua ya 2. Tambua unachotafuta. Muda unaotumika kwa miwani ya miwani kufikia
mto.Hatua ya 3. Jina unachotafuta kwa
kuchagua variable kuwakilisha.Hebu t = wakati. Hatua ya 4. Tafsiri katika equation kwa kuandika formula
sahihi au mfano kwa hali hiyo.
Mbadala katika taarifa iliyotolewa.

Hatua ya 5. Kutatua equation kutumia
mbinu nzuri algebra.

Hatua ya 6. Angalia jibu katika tatizo na
uhakikishe kuwa ni busara.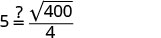

5=5 ✓Je, sekunde 5 zinaonekana kuwa nzuri?
Ndiyo.Hatua ya 7. Jibu swali kwa
sentensi kamili.Itachukua sekunde 5 kwa miwani ya jua ili
kugonga maji.
Helikopta imeshuka mfuko wa uokoaji kutoka kimo cha futi 1,296. Tumia formula\(t=\frac{\sqrt{h}}{4}\) ili kupata sekunde ngapi zilizochukua kwa mfuko ili kufikia chini.
- Jibu
-
Sekunde 9
Washer dirisha imeshuka squeegee kutoka jukwaa 196 miguu juu sidewalk Matumizi formula kupata\(t=\frac{\sqrt{h}}{4}\) jinsi sekunde nyingi ilichukua kwa squeegee kufikia sidewalk.
- Jibu
-
Sekunde 3.5
Maafisa wa polisi wanachunguza ajali za gari hupima urefu wa alama za skid kwenye lami. Kisha hutumia mizizi ya mraba kuamua kasi, kwa maili kwa saa, gari lilikuwa linakwenda kabla ya kutumia breki.
Ikiwa urefu wa alama za skid ni d miguu, basi kasi, s, ya gari kabla ya breki kutumika inaweza kupatikana kwa kutumia formula,
\(s=\sqrt{24d}\)
Baada ya ajali ya gari, alama za skid kwa gari moja zilipima miguu 190. Tumia formula\(s=\sqrt{24d}\) ili kupata kasi ya gari kabla ya breki zilitumiwa. Pindua jibu lako kwa karibu kumi.
- Jibu
-
Hatua ya 1. Soma tatizo. Hatua ya 2. Tambua kile tunachotafuta. Kasi ya gari. Hatua ya 3. Jina kile tunachotafuta. Hebu s = kasi. Hatua ya 4. Tafsiri katika equation kwa kuandika formula sahihi. 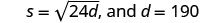
Badilisha taarifa iliyotolewa. 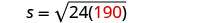
Hatua ya 5. Kutatua equation. 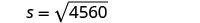
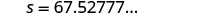
Pande zote hadi mahali 1 ya decimal. 
Hatua ya 6. Angalia jibu katika tatizo.
67.5≈? 24 (190) √
67.5≈? 4560 √
67.5≈? 67.5277...Je, 67.5 mph kasi ya kuridhisha? Ndiyo. Hatua ya 7. Jibu swali kwa sentensi kamili. Kasi ya gari ilikuwa takriban maili 67.5 kwa saa.
Mpelelezi wa ajali alipima alama za skid za gari. Urefu wa alama za skid ulikuwa miguu 76. Tumia formula\(s=\sqrt{24d}\) ili kupata kasi ya gari kabla ya breki zilitumiwa. Pindua jibu lako kwa karibu kumi.
- Jibu
-
Futi 42.7
Alama za skid za gari lililohusika katika ajali zilikuwa na urefu wa futi 122. Tumia formula\(s=\sqrt{24d}\) ili kupata kasi ya gari kabla ya breki zilitumika. Pindua jibu lako kwa karibu kumi.
- Jibu
-
Futi 54.1
Dhana muhimu
- Kutatua Equation Radical:
- Isulate radical upande mmoja wa equation.
- Square pande zote mbili za equation.
- Kutatua equation mpya.
- Angalia jibu. Baadhi ya ufumbuzi kupatikana inaweza kufanya kazi katika equation awali.
- Kutatua Maombi na Fomu
- Soma tatizo na uhakikishe maneno yote na mawazo yanaeleweka. Ikiwa inafaa, futa takwimu na uifanye alama kwa habari iliyotolewa.
- Tambua kile tunachotafuta.
- Jina kile tunachotafuta kwa kuchagua variable kuwakilisha.
- Tafsiri katika equation kwa kuandika formula sahihi au mfano kwa hali hiyo. Mbadala katika taarifa iliyotolewa.
- Kutatua equation kutumia mbinu nzuri algebra.
- Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
- Jibu swali kwa sentensi kamili.
- Eneo la Mraba
- vitu kuanguka
- Duniani, ikiwa kitu kimeshuka kutoka urefu wa miguu ya hh, muda katika sekunde itachukua kufikia ardhi hupatikana kwa kutumia formula\(t=\frac{\sqrt{h}}{4}\).
- Skid Marks na kasi ya gari
- Ikiwa urefu wa alama za skid ni d miguu, basi kasi, s, ya gari kabla ya breki kutumika inaweza kupatikana kwa kutumia formula\(s=\sqrt{24d}\).
faharasa
- equation radical
- Equation ambayo variable iko katika radicand ya mizizi ya mraba inaitwa equation radical


