9.5E: Mazoezi
- Page ID
- 177359
Mazoezi hufanya kamili
Gawanya Mizizi ya mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\frac{\sqrt{27}}{6}\)
- Jibu
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{\sqrt{50}}{10}\)
\(\frac{\sqrt{72}}{9}\)
- Jibu
-
\(\frac{2\sqrt{2}}{3}\)
\(\frac{\sqrt{243}}{6}\)
\(\frac{2−\sqrt{32}}{8}\)
- Jibu
-
\(\frac{1−2\sqrt{2}}{4}\)
\(\frac{3+\sqrt{27}}{9}\)
\(\frac{6+\sqrt{45}}{6}\)
- Jibu
-
\(\frac{2+\sqrt{5}}{2}\)
\(\frac{10−\sqrt{200}}{20}\)
\(\frac{\sqrt{80}}{\sqrt{125}}\)
- Jibu
-
\(\frac{4}{5}\)
\(\frac{\sqrt{72}}{\sqrt{200}}\)
\(\frac{\sqrt{128}}{\sqrt{72}}\)
- Jibu
-
\(\frac{4}{3}\)
\(\frac{\sqrt{48}}{\sqrt{75}}\)
- \(\frac{\sqrt{8x^6}}{2x^2}\)
- \(\frac{\sqrt{200m^5}}{98m}\)
- Jibu
-
- \(2x^2\)
- \(\frac{10m^2}{7}\)
- \(\frac{\sqrt{10y^3}}{5y}\)
- \(\frac{\sqrt{108n^7}}{243n^3}\)
\(\frac{\sqrt{75r^3}}{108r}\)
- Jibu
-
\(\frac{5r}{6}\)
\(\frac{\sqrt{196q^5}}{484q}\)
\(\frac{\sqrt{108p^{5}q^{2}}}{\sqrt{34p^{3}q^{6}}}\)
- Jibu
-
\(\frac{3p\sqrt{102}}{17q^2}\)
\(\frac{\sqrt{98rs^{10}}}{\sqrt{2r^{3}s^{4}}}\)
\(\frac{\sqrt{320mn^{5}}}{\sqrt{45m^{7}n^{3}}}\)
- Jibu
-
\(\frac{8n}{3m^3}\)
\(\frac{\sqrt{810c^{3}d^{7}}}{\sqrt{1000c^{5}d}}\)
\(\frac{\sqrt{98}}{14}\)
- Jibu
-
\(\frac{\sqrt{2}}{2}\)
\(\frac{\sqrt{72}}{18}\)
\(\frac{5+\sqrt{125}}{15}\)
- Jibu
-
\(\frac{1+\sqrt{3}}{3}\)
\(\frac{6−\sqrt{45}}{12}\)
\(\frac{\sqrt{96}}{\sqrt{150}}\)
- Jibu
-
\(\frac{4}{5}\)
\(\frac{\sqrt{28}}{\sqrt{63}}\)
\(\frac{\sqrt{26y^7}}{2y}\)
- Jibu
-
\(y^3\sqrt{13}\)
\(\frac{\sqrt{15x^3}}{\sqrt{3x}}\)
Rationalize Denominator ya Muda mmoja
Katika mazoezi yafuatayo, kurahisisha na kuimarisha denominator.
\(\frac{10}{\sqrt{6}}\)
- Jibu
-
\(\frac{5\sqrt{6}}{3}\)
\(\frac{8}{\sqrt{3}}\)
\(\frac{6}{\sqrt{7}}\)
- Jibu
-
\(\frac{6\sqrt{7}}{7}\)
\(\frac{4}{\sqrt{5}}\)
\(\frac{3}{\sqrt{13}}\)
- Jibu
-
\(\frac{3\sqrt{13}}{13}\)
\(\frac{10}{\sqrt{11}}\)
\(\frac{10}{3\sqrt{10}}\)
- Jibu
-
\(\frac{\sqrt{10}}{3}\)
\(\frac{2}{5\sqrt{2}}\)
\(\frac{4}{9\sqrt{5}}\)
- Jibu
-
\(\frac{4\sqrt{5}}{45}\)
\(\frac{9}{2\sqrt{7}}\)
\(−\frac{9}{2\sqrt{3}}\)
- Jibu
-
\(−\frac{3\sqrt{3}}{2}\)
\(−\frac{8}{3\sqrt{6}}\)
\(\sqrt{\frac{3}{20}}\)
- Jibu
-
\(\frac{\sqrt{15}}{10}\)
\(\sqrt{\frac{4}{27}}\)
\(\sqrt{\frac{7}{40}}\)
- Jibu
-
\(\frac{\sqrt{70}}{20}\)
\(\sqrt{\frac{8}{45}}\)
\(\sqrt{\frac{19}{175}}\)
- Jibu
-
\(\frac{\sqrt{133}}{35}\)
\(\sqrt{\frac{17}{192}}\)
Rationalize Denominator ya Muda Mbili
Katika mazoezi yafuatayo, kurahisisha kwa kupitisha denominator.
- \(\frac{3}{3+\sqrt{11}}\)
- \(\frac{8}{1−\sqrt{5}}\)
- Jibu
-
- \(\frac{3(3−\sqrt{11})}{−2}\)
- \(−2(1+\sqrt{5})\)
- \(\frac{4}{4+\sqrt{7}}\)
- \(\frac{7}{2−\sqrt{6}}\)
- \(\frac{5}{5+\sqrt{6}}\)
- \(\frac{6}{3−\sqrt{7}}\)
- Jibu
-
- \(\frac{5(5−\sqrt{6})}{19}\)
- \(3(3+\sqrt{7})\)
- \(\frac{6}{6+\sqrt{5}}\)
- \(\frac{5}{4−\sqrt{11}}\)
\(\frac{\sqrt{3}}{\sqrt{m}−\sqrt{5}}\)
- Jibu
-
\(\frac{\sqrt{3}(\sqrt{m}+\sqrt{5})}{m−5}\)
\(\frac{\sqrt{5}}{\sqrt{n}−\sqrt{7}}\)
\(\frac{\sqrt{2}}{\sqrt{x}−\sqrt{6}}\)
- Jibu
-
\(\frac{\sqrt{2}(\sqrt{x}+\sqrt{3})}{x−6}\)
\(\frac{\sqrt{7}}{\sqrt{y}+\sqrt{3}}\)
\(\frac{\sqrt{r}+\sqrt{5}}{\sqrt{r}−\sqrt{5}}\)
- Jibu
-
\(\frac{(\sqrt{r}+\sqrt{5})^2}{r−5}\)
\(\frac{\sqrt{s}−\sqrt{6}}{\sqrt{s}+\sqrt{6}}\)
\(\frac{\sqrt{150x^{2}y^{6}}}{\sqrt{6x^{4}y^{2}}}\)
- Jibu
-
\(\frac{5y^2}{x}\)
\(\frac{\sqrt{80p^{3}q}}{\sqrt{5pq^{5}}}\)
\(\frac{15}{\sqrt{5}}\)
- Jibu
-
\(3\sqrt{5}\)
\(\frac{3}{5\sqrt{8}}\)
\(\sqrt{\frac{8}{54}}\)
- Jibu
-
\(\frac{2\sqrt{3}}{9}\)
\(\sqrt{\frac{12}{20}}\)
\(\frac{3}{5+\sqrt{5}}\)
- Jibu
-
\(\frac{3(5−\sqrt{5})}{20}\)
\(\frac{20}{4−\sqrt{3}}\)
\(\frac{\sqrt{2}}{\sqrt{x}−\sqrt{3}}\)
- Jibu
-
\(\frac{\sqrt{2}(\sqrt{x}+\sqrt{3})}{x−3}\)
\(\frac{\sqrt{5}}{\sqrt{y}−\sqrt{7}}\)
\(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}−\sqrt{8}}\)
- Jibu
-
\(\frac{(\sqrt{x}+2\sqrt{2})^2}{x−8}\)
\(\frac{\sqrt{m}−\sqrt{3}}{\sqrt{m}+\sqrt{3}}\)
kila siku Math
Kitanda cha usambazaji kinashuka kutoka ndege inayopuka kwenye urefu wa miguu 250. \(\sqrt{\frac{250}{16}}\)Kurahisisha kuamua sekunde ngapi inachukua kwa kit cha usambazaji kufikia ardhi.
- Jibu
-
\(\frac{5\sqrt{10}}{4}\)sekunde
Flare imeshuka ndani ya bahari kutoka ndege inayopuka kwenye urefu wa miguu 1,200. \(\sqrt{\frac{1200}{16}}\)Kurahisisha kuamua sekunde ngapi inachukua kwa flare kufikia bahari.
Mazoezi ya kuandika
- Kurahisisha\(\sqrt{\frac{27}{3}}\) na kuelezea hatua zako zote.
- Kurahisisha\(\sqrt{\frac{27}{5}}\) na kuelezea hatua zako zote.
- Kwa nini njia mbili za kurahisisha mizizi ya mraba tofauti?
- Jibu
-
Majibu yatatofautiana.
- Takriban\(\frac{1}{\sqrt{2}}\) kwa kugawa\(\frac{1}{1.414}\) kwa kutumia mgawanyiko mrefu bila calculator.
- Rationalizing denominator ya\(\frac{1}{\sqrt{2}}\) anatoa\(\frac{\sqrt{2}}{2}\). Takriban\(\frac{\sqrt{2}}{2}\) kwa kugawa\(\frac{1.414}{2}\) kwa kutumia mgawanyiko mrefu bila calculator.
- Je, unakubaliana kwamba rationalizing denominator inafanya mahesabu rahisi? Kwa nini au kwa nini?
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
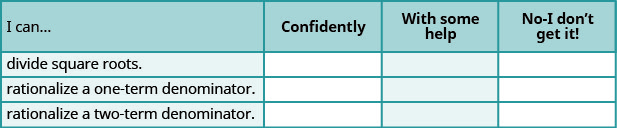
ⓑ Baada ya kuangalia orodha, unafikiri umeandaliwa vizuri kwa sehemu inayofuata? Kwa nini au kwa nini?


