Skip to main content
Global

9.5: Gawanya mizizi ya Mraba

  1. Last updated
  2. Save as PDF
  • Page ID
    177340

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Gawanya mizizi ya mraba
    • Rationalize denominator ya muda mmoja
    • Rationalize denominator mbili mrefu
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kupata sehemu sawa\(\frac{5}{8}\) na na denominator 48.
      Kama amekosa tatizo hili, kupitia Zoezi 1.6.1.
    2. Kurahisisha:\((\sqrt{5})^2\).
      Kama amekosa tatizo hili, mapitio Mfano 9.4.13.
    3. Panua: (7+3x) (7-3x).
      Kama amekosa tatizo hili, kupitia Zoezi 6.4.22.

    Gawanya Mizizi ya mraba

    Tunajua kwamba sisi kurahisisha sehemu kwa kuondoa mambo ya kawaida kwa nambari na denominator. Tunapokuwa na sehemu na mizizi ya mraba katika namba, sisi kwanza tunapunguza mizizi ya mraba. Kisha tunaweza kuangalia mambo ya kawaida.

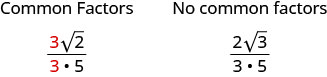
    Takwimu hii inaonyesha nguzo mbili. Ya kwanza inaitwa “Mambo ya kawaida” na ina mara 3 mizizi ya mraba ya 2 zaidi ya mara 3 5 chini yake. Wote namba tatu ni nyekundu. Safu ya pili inaitwa “Hakuna mambo ya kawaida” na ina mara 2 mizizi ya mraba ya 3 zaidi ya mara 3 5.

    Mfano\(\PageIndex{1}\)

    Kurahisisha:\(\frac{\sqrt{54}}{6}\)

    Jibu
      \(\frac{\sqrt{54}}{6}\)
    Kurahisisha radical. \(\frac{\sqrt{9}·\sqrt{6}}{6}\)
    Kurahisisha. \(\frac{3\sqrt{6}}{6}\)
    Ondoa mambo ya kawaida. \(\frac{3\sqrt{6}}{3·2}\)
    Kurahisisha. \(\frac{\sqrt{6}}{2}\)
    Mfano\(\PageIndex{2}\)

    Kurahisisha:\(\frac{\sqrt{32}}{8}\).

    Jibu

    \(\frac{\sqrt{2}}{2}\)

    Mfano\(\PageIndex{3}\)

    Kurahisisha:\(\frac{\sqrt{75}}{15}\).

    Jibu

    \(\frac{\sqrt{3}}{3}\)

    Mfano\(\PageIndex{4}\)

    Kurahisisha:\(\frac{6−\sqrt{24}}{12}\).

    Jibu
      \(\frac{6−\sqrt{24}}{12}\)
    Kurahisisha radical. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\)
    Kurahisisha. \(\frac{6−2\sqrt{6}}{12}\)
    Fanya sababu ya kawaida kutoka kwa nambari. \(\frac{2(3−\sqrt{6})}{12}\)
    Ondoa mambo ya kawaida. \(\frac{2(3−\sqrt{6})}{2·6}\)
    Kurahisisha. \(\frac{3−\sqrt{6}}{6}\)
    Mfano\(\PageIndex{5}\)

    Kurahisisha:\(\frac{8−\sqrt{40}}{10}\).

    Jibu

    \(\frac{4−\sqrt{10}}{5}\)

    Mfano\(\PageIndex{6}\)

    Kurahisisha:\(\frac{10−\sqrt{75}}{20}\).

    Jibu

    \(\frac{5−\sqrt{3}}{4}\)

    Tumetumia Mali ya Quotient ya Mizizi ya Mraba ili kurahisisha mizizi ya mraba ya sehemu ndogo. Mali Quotient ya mizizi Square anasema

    \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\),\(b \ne 0\).

    Wakati mwingine tutahitaji kutumia Mali ya Quotient ya Mizizi ya Mraba 'katika reverse' ili kurahisisha sehemu na mizizi ya mraba.

    \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\),\(b \ne 0\).

    Tutaandika upya Mali ya Quotient ya Mizizi ya Mraba ili tuone njia zote mbili pamoja. Kumbuka: tunadhani vigezo vyote ni kubwa kuliko au sawa na sifuri ili mizizi yao ya mraba ni namba halisi.

    Ufafanuzi: QUOTIENT PROPERTY YA SQUARE ROOTS

    Ikiwa, b ni namba zisizo hasi halisi na\(b \ne 0\), basi

    \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)na\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)

    Tutatumia Mali ya Quotient ya Mizizi ya Mraba 'katika reverse' wakati sehemu tunayoanza na ni quotient ya mizizi miwili ya mraba, na wala radicand ni mraba kamilifu. Tunapoandika sehemu katika mizizi moja ya mraba, tunaweza kupata mambo ya kawaida katika nambari na denominator.

    Mfano\(\PageIndex{7}\)

    Kurahisisha:\(\frac{\sqrt{27}}{\sqrt{75}}\)

    Jibu
      \(\frac{\sqrt{27}}{\sqrt{75}}\)
    Wala radicand ni mraba kamili, hivyo uandike tena kwa kutumia mali ya quotient ya mizizi ya mraba. \(\sqrt{\frac{27}{75}}\)
    Ondoa mambo ya kawaida katika nambari na denominator. \(\sqrt{\frac{9}{25}}\)
    Kurahisisha. \(\frac{3}{5}\)
    Mfano\(\PageIndex{8}\)

    Kurahisisha:\(\frac{\sqrt{48}}{\sqrt{108}}\)

    Jibu

    \(\frac{2}{3}\)

    Mfano\(\PageIndex{9}\)

    Kurahisisha:\(\frac{\sqrt{96}}{\sqrt{54}}\)

    Jibu

    \(\frac{4}{3}\)

    Tutatumia Quotient Mali kwa Exponents,\(\frac{a^m}{a^n}=a^{m−n}\), wakati tuna vigezo na exponents katika radicands.

    Mfano\(\PageIndex{10}\)

    Kurahisisha:\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)

    Jibu
      \(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
    Wala radicand ni mraba kamili, hivyo uandike tena kwa kutumia mali ya quotient ya mizizi ya mraba. \(\sqrt{\frac{6y^5}{2y}}\)
    Ondoa mambo ya kawaida katika nambari na denominator. \(\sqrt{3y^4}\)
    Kurahisisha. \(y^2\sqrt{3}\)
    Mfano\(\PageIndex{11}\)

    Kurahisisha:\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).

    Jibu

    \(r\sqrt{2}\)

    Mfano\(\PageIndex{12}\)

    Kurahisisha:\(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)

    Jibu

    \(p^2\sqrt{7}\)

    Mfano\(\PageIndex{13}\)

    Kurahisisha:\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)

    Jibu
      \(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
    Andika upya kutumia mali ya quotient ya mizizi ya mraba. \(\sqrt{\frac{72x^3}{162x}}\)
    Ondoa mambo ya kawaida. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\)
    Kurahisisha. \(\sqrt{\frac{4x^2}{9}}\)
    Kurahisisha radical. \(\frac{2x}{3}\)
    Mfano\(\PageIndex{14}\)

    Kurahisisha:\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).

    Jibu

    \(\frac{5s}{8}\)

    Mfano\(\PageIndex{15}\)

    Kurahisisha:\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).

    Jibu

    \(\frac{5q^2}{6}\)

    Mfano\(\PageIndex{16}\)

    Kurahisisha:\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).

    Jibu
      \(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\)
    Andika upya kutumia mali ya quotient ya mizizi ya mraba. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\)
    Ondoa mambo ya kawaida. \ (\ sqrt {\ frac {49b ^ 4} {a ^ 2}}\
    Kurahisisha radical. \(\frac{7b^2}{a}\)
    Mfano\(\PageIndex{17}\)

    Kurahisisha:\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).

    Jibu

    \(\frac{9x^2}{y^2}\)

    Mfano\(\PageIndex{18}\)

    Kurahisisha:\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).

    Jibu

    \(\frac{10n^3}{m}\)

    Tambua Denominator ya Muda Mmoja

    Kabla ya calculator kuwa chombo cha maisha ya kila siku, meza za mizizi ya mraba zilitumiwa kupata maadili ya karibu ya mizizi ya mraba. Kielelezo kinaonyesha sehemu ya meza ya mraba na mizizi ya mraba. Mizizi ya mraba inakaribia maeneo tano ya decimal katika meza hii.

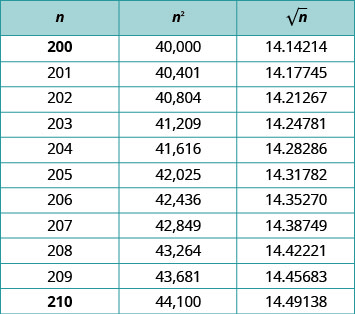
    Jedwali hili lina safu tatu na safu kumi na moja. Nguzo zimeandikwa, “n,” “n mraba,” na “mizizi ya mraba ya n.” Chini ya safu iliyoitwa “n” ni namba zifuatazo: 200; 201; 202; 203; 204; 205; 206; 207; 208; 209; na 210. Chini ya safu iliyoandikwa, “n mraba” ni namba zifuatazo: 40,000; 40,401; 40,804; 41,209; 41,616; 42,025; 42,436; 42,849; 43,264; 43,681; 44,100. Chini ya safu iliyoandikwa, “mizizi ya mraba ya n” ni namba zifuatazo: 14.14214; 14.17745; 14.21267; 14.24781; 14.28286; 14.31782; 14.35270; 14.38749; 14.42221; 14.45683; 14.49138.
    Jedwali la mizizi ya mraba ilitumiwa kupata maadili ya takriban ya mizizi ya mraba kabla ya kuwa na mahesabu.

    Ikiwa mtu anahitaji takriban sehemu na mizizi ya mraba katika denominator, ilimaanisha kufanya mgawanyiko mrefu na mgawanyiko wa mahali pa decimal tano. Hii ilikuwa mchakato mbaya sana.

    Kwa sababu hii, mchakato unaoitwa rationalizing denominator ulianzishwa. Sehemu yenye radical katika denominator inabadilishwa kwa sehemu sawa ambayo denominator ni integer. Utaratibu huu bado unatumika leo na ni muhimu katika maeneo mengine ya hisabati, pia.

    Ufafanuzi: RATIONALIZING DENOMINATOR

    Mchakato wa kubadili sehemu na radical katika denominator kwa sehemu sawa ambayo denominator ni integer inaitwa rationalizing denominator.

    Mizizi ya mraba ya namba ambazo si mraba kamili ni namba zisizo na maana. Wakati sisi rationalize denominator, sisi kuandika sehemu sawa na idadi ya busara katika denominator.

    Hebu tuangalie mfano wa namba.

    \[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]

    Lakini tunaweza kupata sehemu sawa na\(\frac{1}{\sqrt{2}}\) kwa kuzidisha nambari na denominator na\(\sqrt{2}\).

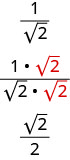
    Takwimu hii inaonyesha sehemu tatu. Sehemu ya kwanza ni 1 juu ya mizizi ya mraba ya 2. Ya pili ni mara 1 mizizi ya mraba ya 2 juu ya mizizi ya mraba ya mara 2 mizizi ya mraba ya 2. Ya tatu inaonyesha mizizi ya mraba ya 2 juu ya 2.

    Sasa ikiwa tunahitaji thamani ya takriban, tunagawanya\(2) \overline{1.41421}\). Hii ni rahisi sana.

    Ingawa tuna calculators inapatikana karibu kila mahali, sehemu na radical katika denominator bado lazima rationalized. Haifikiriwa kuwa rahisi kama denominator ina mizizi ya mraba.

    Vile vile, mizizi ya mraba haipatikani kuwa rahisi ikiwa radicand ina sehemu.

    Ufafanuzi: SQUARE ROOTS RAHISI

    Mizizi ya mraba inachukuliwa kuwa rahisi ikiwa kuna

    • hakuna sababu kamilifu za mraba katika radicand
    • hakuna sehemu ndogo katika radicand
    • hakuna mizizi ya mraba katika denominator ya sehemu

    Kwa rationalize denominator, sisi kutumia mali\((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.

    Tutatumia mali hii kwa rationalize denominator katika mfano unaofuata.

    Mfano\(\PageIndex{19}\)

    Kurahisisha:\(\frac{4}{\sqrt{3}}\).

    Jibu

    Ili kuondoa mizizi ya mraba kutoka kwa denominator, tunaizidisha yenyewe. Ili kuweka sehemu ndogo sawa, tunazidisha nambari zote na denominator kwa sababu sawa.

      \(\frac{4}{\sqrt{3}}\)

    Panua nambari zote mbili na denominator kwa\(\sqrt{3}\)    		 \(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\)
    Kurahisisha. \(\frac{4\sqrt{3}}{3}\)
    Mfano\(\PageIndex{20}\)

    Kurahisisha:\(\frac{5}{\sqrt{3}}\).

    Jibu

    \(\frac{5\sqrt{3}}{3}\)

    Mfano\(\PageIndex{21}\)

    Kurahisisha:\(\frac{6}{\sqrt{5}}\).

    Jibu

    \(\frac{6\sqrt{5}}{5}\)

    Mfano\(\PageIndex{22}\)

    Kurahisisha:\(−\frac{8}{3\sqrt{6}}\)

    Jibu

    Ili kuondoa mizizi ya mraba kutoka kwa denominator, tunaizidisha yenyewe. Ili kuweka sehemu ndogo sawa, tunazidisha nambari zote na denominator na\(\sqrt{6}\).

      .
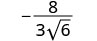
    Panua nambari zote mbili na denominator na\(\sqrt{6}\). .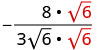
    Kurahisisha. .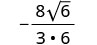
    Ondoa mambo ya kawaida. .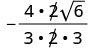
    Kurahisisha. .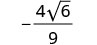
    Mfano\(\PageIndex{23}\)

    Kurahisisha:\(\frac{5}{2\sqrt{5}}\).

    Jibu

    \(\frac{\sqrt{5}}{2}\)

    Mfano\(\PageIndex{24}\)

    Kurahisisha:\(−\frac{9}{4\sqrt{3}}\).

    Jibu

    \(−\frac{3\sqrt{3}}{4}\)

    Daima kurahisisha radical katika denominator kwanza, kabla ya kuifanya. Kwa njia hii idadi hukaa ndogo na rahisi kufanya kazi na.

    Mfano\(\PageIndex{25}\)

    Kurahisisha:\(\sqrt{\frac{5}{12}}\).

    Jibu
      .
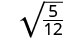
    Sehemu sio mraba kamili, hivyo uandike upya kwa kutumia Mali ya
    Quotient.    		 .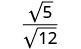
    Kurahisisha denominator. .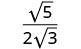
    Rationalize denominator. .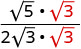
    Kurahisisha. .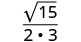
    Kurahisisha. .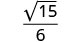
    Mfano\(\PageIndex{26}\)

    Kurahisisha:\(\sqrt{\frac{7}{18}}\).

    Jibu

    \(\frac{\sqrt{14}}{6}\)

    Mfano\(\PageIndex{27}\)

    Kurahisisha:\(\sqrt{\frac{3}{32}}\).

    Jibu

    \(\frac{\sqrt{6}}{8}\)

    Mfano\(\PageIndex{28}\)

    Kurahisisha:\(\sqrt{\frac{11}{28}}\)

    Jibu
      .
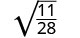
    Andika upya kwa kutumia Mali ya Quotient. .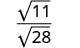
    Kurahisisha denominator. .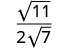
    Rationalize denominator. .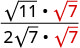
    Kurahisisha. .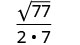
    Kurahisisha. .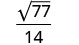
    Mfano\(\PageIndex{29}\)

    Kurahisisha:\(\sqrt{\frac{3}{27}}\).

    Jibu

    \(\frac{1}{3}\)

    Mfano\(\PageIndex{30}\)

    Kurahisisha:\(\sqrt{\frac{10}{50}}\)

    Jibu

    \(\frac{\sqrt{5}}{5}\)

    Tambua Denominator ya Muda Mbili

    Wakati denominator ya sehemu ni jumla au tofauti na mizizi ya mraba, tunatumia muundo wa Bidhaa ya Conjugates ili kurekebisha denominator.

    \[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]

    Tunapozidisha binomial ambayo inajumuisha mizizi ya mraba na mchanganyiko wake, bidhaa haina mizizi ya mraba.

    Mfano\(\PageIndex{31}\)

    Kurahisisha:\(\frac{4}{4+\sqrt{2}}\).

    Jibu
      .
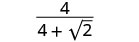
    Panua nambari na denominator kwa conjugate ya denominator. .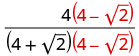
    Kuzidisha conjugates katika denominator. .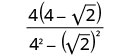
    Kurahisisha denominator. .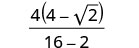
    Kurahisisha denominator. .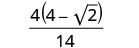
    Ondoa mambo ya kawaida kutoka kwa nambari na denominator. .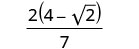
    Tunaacha nambari katika fomu iliyosababishwa ili iwe rahisi kuangalia mambo ya kawaida baada ya kurahisisha denominator.  
    Mfano\(\PageIndex{32}\)

    Kurahisisha:\(\frac{2}{2+\sqrt{3}}\).

    Jibu

    \(\frac{2(2−\sqrt{3})}{1}\)

    Mfano\(\PageIndex{33}\)

    Kurahisisha:\(\frac{5}{5+\sqrt{3}}\).

    Jibu

    \(\frac{5(5−\sqrt{3})}{22}\)

    Mfano\(\PageIndex{34}\)

    Kurahisisha:\(\frac{5}{2−\sqrt{3}}\).

    Jibu
      .
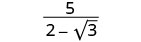
    Panua nambari na denominator kwa conjugate ya denominator. .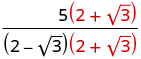
    Kuzidisha conjugates katika denominator. .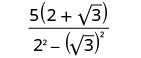
    Kurahisisha denominator. .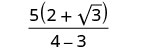
    Kurahisisha denominator. .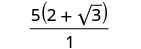
    Kurahisisha. .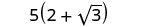
    Mfano\(\PageIndex{35}\)

    Kurahisisha:\(\frac{3}{1−\sqrt{5}}\).

    Jibu

    \(−\frac{3(1+\sqrt{5})}{4}\)

    Mfano\(\PageIndex{36}\)

    Kurahisisha:\(\frac{2}{4−\sqrt{6}}\).

    Jibu

    \(\frac{4+\sqrt{6}}{5}\)

    Mfano\(\PageIndex{37}\)

    Kurahisisha:\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).

    Jibu
      .
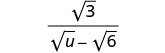
    Panua nambari na denominator kwa conjugate ya denominator. .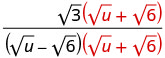
    Kuzidisha conjugates katika denominator. .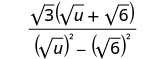
    Kurahisisha denominator. .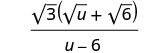
    Mfano\(\PageIndex{38}\)

    Kurahisisha:\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).

    Jibu

    \(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)

    Mfano\(\PageIndex{39}\)

    Kurahisisha:\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).

    Jibu

    \(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)

    Mfano\(\PageIndex{40}\)

    Kurahisisha:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).

    Jibu
      .
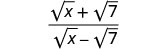
    Panua nambari na denominator kwa conjugate ya denominator. .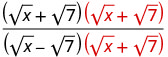
    Kuzidisha conjugates katika denominator. .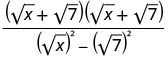
    Kurahisisha denominator. .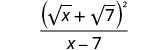
    Hatuna mraba namba. Kwa fomu iliyosababishwa, tunaweza kuona hakuna sababu za kawaida za kuondoa kutoka kwa nambari na denominator.  
    Mfano\(\PageIndex{41}\)

    Kurahisisha:\(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).

    Jibu

    \(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)

    Mfano\(\PageIndex{42}\)

    Kurahisisha:\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).

    Jibu

    \(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kugawanya na kugawa.

    • Kugawanya na Kutambua

    Dhana muhimu

    • Mali ya Quotient ya Mizizi ya Mraba
      • Ikiwa, b ni namba zisizo hasi halisi na\(b \ne 0\), basi

        \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)na\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)

    • Mizizi
      ya mraba iliyorahisishwa       Mizizi ya mraba inachukuliwa kuwa rahisi ikiwa kuna
      • hakuna sababu za mraba kamili katika radicand
      • hakuna sehemu ndogo katika radicand
      • hakuna mizizi ya mraba katika denominator ya sehemu

    faharasa

    rationalizing denominator
    Mchakato wa kubadili sehemu na radical katika denominator kwa sehemu sawa ambayo denominator ni integer inaitwa rationalizing denominator.