9.4E: Mazoezi
- Page ID
- 177375
Mazoezi hufanya kamili
Kuzidisha mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt{2}·\sqrt{8}\)
- \((3\sqrt{3})(2\sqrt{18})\)
- Jibu
-
- \(44\)
- \(18\sqrt{6}\)
- \(\sqrt{6}·\sqrt{6}\)
- \((3\sqrt{2})(2\sqrt{32})\)
- \(\sqrt{7}·\sqrt{14}\)
- \((4\sqrt{8})(5\sqrt{8})\)
- Jibu
-
- \(7\sqrt{2}\)
- 160
- \(\sqrt{6}·\sqrt{12}\)
- \((2\sqrt{5})(2\sqrt{10})\)
\((5\sqrt{2})(3\sqrt{6})\)
- Jibu
-
\(30\sqrt{3}\)
\((2\sqrt{3})(4\sqrt{6})\)
\((−2\sqrt{3})(3\sqrt{18})\)
- Jibu
-
\(−18\sqrt{6}\)
\((−4\sqrt{5})(5\sqrt{10})\)
\((5\sqrt{6})(−\sqrt{12})\)
- Jibu
-
\(−30\sqrt{2}\)
\((6\sqrt{2})(−\sqrt{10})\)
\((−2\sqrt{7})(−2\sqrt{14})\)
- Jibu
-
\(28\sqrt{2}\)
\((−2\sqrt{11})(−4\sqrt{22})\)
- \((\sqrt{15y})(\sqrt{5y^3})\)
- \((\sqrt{2n^2})(\sqrt{18n^3})\)
- Jibu
-
- \(5y^2\sqrt{3}\)
- \(6n^2\sqrt{n}\)
- \((\sqrt{14x^3})(\sqrt{7x^3})\)
- \((\sqrt{3q^2})(\sqrt{48q^3})\)
- \((\sqrt{16y^2})(\sqrt{8y^4})\)
- \((\sqrt{11s^6})(\sqrt{11s})\)
- Jibu
-
- \(8y^3\sqrt{2}\)
- \(11s^3\sqrt{s}\)
ⓐ\((\sqrt{8x^3})(\sqrt{3x})\)
ⓑ\((\sqrt{7r})(\sqrt{7r^8})\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
- Jibu
-
\(40b^2\sqrt{3}\)
\((\sqrt{38c^5})(\sqrt{26c^3})\)
\((6\sqrt{3d^3})(4\sqrt{12d^5})\)
- Jibu
-
\(144d^4\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
\((2\sqrt{5d^6})(3\sqrt{20d^2})\)
- Jibu
-
\(60d^4\)
\((−2\sqrt{7z^3})(3\sqrt{14z^8})\)
\((4\sqrt{2k^5})(−3\sqrt{32k^6})\)
- Jibu
-
\(−96k^5\sqrt{k}\)
- \((\sqrt{7})^2\)
- \((−\sqrt{15})^2\)
- \((\sqrt{11})^2\)
- \((−\sqrt{21})^2\)
- Jibu
-
- 11
- 21
- \((\sqrt{19})^2\)
- \((−\sqrt{5})^2\)
- \((\sqrt{23})^2\)
- \((−\sqrt{3})^2\)
- Jibu
-
- 23
- 3
- \((4\sqrt{11})(−3\sqrt{11})\)
- \((5\sqrt{3})^2\)
- \((2\sqrt{13})(−9\sqrt{13})\)
- \((6\sqrt{5})^2\)
- Jibu
-
- -234
- 180
- \((−3\sqrt{12})(−2\sqrt{6})\)
- \( (−4\sqrt{10})^2\)
- \((−7\sqrt{5})(−3\sqrt{10})\)
- \( (−2\sqrt{14})^2\)
- Jibu
-
- \(105\sqrt{2}\)
- 56
Tumia Uzidishaji wa Polynomial ili Kuzidisha Mizizi
Katika mazoezi yafuatayo, kurahisisha.
- \(3(4−\sqrt{3})\)
- \(\sqrt{2}(4−\sqrt{6})\)
- \(4(6−\sqrt{11})\)
- \(\sqrt{2}(5−\sqrt{12})\)
- Jibu
-
- \(24−4\sqrt{11}\)
- \(5\sqrt{2}−2\sqrt{6}\)
- \(5(3−\sqrt{7})\)
- \(\sqrt{3}(4−\sqrt{15})\)
- \(7(−2−\sqrt{11})\)
- \(\sqrt{7}(6−\sqrt{14})\)
- Jibu
-
- \(−14−7\sqrt{11}\)
- \(6\sqrt{7}−7\sqrt{2}\)
- \(\sqrt{7}(5+2\sqrt{7})\)
- \(\sqrt{5}(\sqrt{10}+\sqrt{18})\)
- \(\sqrt{11}(8+4\sqrt{11})\)
- \(\sqrt{3}(\sqrt{12}+\sqrt{27})\)
- Jibu
-
- \(44+8\sqrt{11}\)
- 15
- \(\sqrt{11}(−3+4\sqrt{1})\)
- \(\sqrt{3}(\sqrt{15}−\sqrt{18})\)
- \(\sqrt{2}(−5+9\sqrt{2})\)
- \(\sqrt{7}(\sqrt{3}−\sqrt{21})\)
- Jibu
-
- \(18−5\sqrt{2}\)
- \(\sqrt{21}−7\sqrt{3}\)
\((8+\sqrt{3})(2−\sqrt{3})\)
\((7+\sqrt{3})(9−\sqrt{3})\)
- Jibu
-
\(60+2\sqrt{3}\)
\((8−\sqrt{2})(3+\sqrt{2})\)
\((9−\sqrt{2})(6+\sqrt{2})\)
- Jibu
-
\(52+3\sqrt{2}\)
\((3−\sqrt{7})(5−\sqrt{7})\)
\((5−\sqrt{7})(4−\sqrt{7})\)
- Jibu
-
\(27−9\sqrt{7}\)
\((1+3\sqrt{10})(5−2\sqrt{10})\)
\((7−2\sqrt{5})(4+9\sqrt{5})\)
- Jibu
-
\(−62+55\sqrt{5}\)
\((\sqrt{3}+\sqrt{10})(\sqrt{3}+2\sqrt{10})\)
\((\sqrt{11}+\sqrt{5})(\sqrt{11}+6\sqrt{5})\)
- Jibu
-
\(41+7\sqrt{55}\)
\((2\sqrt{7}−5\sqrt{11})(4\sqrt{7}+9\sqrt{11})\)
\((4\sqrt{6}+7\sqrt{13})(8\sqrt{6}−3\sqrt{13})\)
- Jibu
-
\(−81+44\sqrt{78}\)
\((5−\sqrt{u})(3+\sqrt{u})\)
\((9−\sqrt{w})(2+\sqrt{w})\)
- Jibu
-
\(18+7\sqrt{w}\)
\((7+2\sqrt{m})(4+9\sqrt{m})\)
\((6+5\sqrt{n})(11+3\sqrt{n})\)
- Jibu
-
\(66+73\sqrt{n}+15n\)
- \((3+\sqrt{5})^2\)
- \((2−5\sqrt{3})^2\)
- \((4+\sqrt{11})^2\)
- \((3−2\sqrt{5})^2\)
- Jibu
-
- \(27+8\sqrt{11}\)
- \(29−12\sqrt{5}\)
- \((9−\sqrt{6})^2\)
- \((10+3\sqrt{7})^2\)
- \((5−\sqrt{10})^2\)
- \((8+3\sqrt{2})^2\)
- Jibu
-
- \(35−10\sqrt{10}\)
- \(82+48\sqrt{2}\)
\((3−\sqrt{5})(3+\sqrt{5})\)
\((10−\sqrt{3})(10+\sqrt{3})\)
- Jibu
-
97
\((4+\sqrt{2})(4−\sqrt{2})\)
\((7+\sqrt{10})(7−\sqrt{10})\)
- Jibu
-
39
\((4+9\sqrt{3})(4−9\sqrt{3})\)
\((1+8\sqrt{2})(1−8\sqrt{2})\)
- Jibu
-
-127
\((12−5\sqrt{5})(12+5\sqrt{5})\)
\((9−4\sqrt{3})(9+4\sqrt{3})\)
- Jibu
-
33
Mazoezi ya mchanganyiko
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{3}·\sqrt{21}\)
\((4\sqrt{6})(−\sqrt{18})\)
- Jibu
-
\(−24\sqrt{3}\)
\((−5+\sqrt{7})(6+\sqrt{21})\)
\((−5\sqrt{7})(6\sqrt{21})\)
- Jibu
-
\(−210\sqrt{3}\)
\((−4\sqrt{2})(2\sqrt{18})\)
\((\sqrt{35y^3})(\sqrt{7y^3})\)
- Jibu
-
\(7y^3\sqrt{5}\)
\((4\sqrt{12x^5})(2\sqrt{6x^3})\)
\((\sqrt{29})^2\)
- Jibu
-
29
\((−4\sqrt{17})(−3\sqrt{17})\)
\((−4+\sqrt{17})(−3+\sqrt{17})\)
- Jibu
-
\(29−7\sqrt{17}\)
kila siku Math
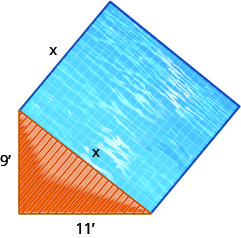
Msanii anataka kuweka bwawa la kutafakari mraba karibu na staha ya triangular, kama inavyoonekana hapa chini. Staha ya triangular ni pembetatu sahihi, na miguu ya urefu wa miguu 9 na miguu 11, na bwawa litakuwa karibu na hypotenuse.
- Tumia Theorem ya Pythagorean ili kupata urefu wa upande wa bwawa. Pindua jibu lako kwa sehemu ya kumi ya karibu ya mguu.
- Pata eneo halisi la bwawa.
Msanii anataka kufanya jiwe ndogo katika sura ya msingi wa mraba uliowekwa na pembetatu sahihi, kama inavyoonyeshwa hapa chini. Msingi wa mraba utakuwa karibu na mguu mmoja wa pembetatu. Mguu mwingine wa pembetatu utapima miguu 2 na hypotenuse itakuwa miguu 5.
- Tumia Theorem ya Pythagorean ili kupata urefu wa upande wa msingi wa mraba. Pindua jibu lako kwa sehemu ya kumi ya karibu ya mguu.
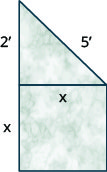
- Pata eneo halisi la uso wa msingi wa mraba.
- Jibu
-
- Futi 4.6
- 21 sq. miguu
Bustani ya mraba itafanywa kwa mpaka wa jiwe kwenye makali moja. Ikiwa\(3+\sqrt{10}\) miguu tu ya mawe inapatikana,\((3+\sqrt{10})^2\) kurahisisha kuamua eneo la bustani kubwa zaidi.
Bustani itafanywa ili kuwa na sehemu mbili za mraba, sehemu moja na\(\sqrt{5}+\sqrt{6}\) yadi za urefu wa upande na sehemu moja na\(\sqrt{2}+\sqrt{3}\) yadi za urefu wa upande. \((\sqrt{5}+\sqrt{6})(\sqrt{2}+\sqrt{3})\)Kurahisisha kuamua eneo la jumla la bustani.
Tuseme sehemu ya tatu itaongezwa kwenye bustani katika zoezi la awali. Sehemu ya tatu ni kuwa na upana wa\(\sqrt{432}\) miguu. Andika maneno ambayo inatoa jumla ya eneo la bustani.
Mazoezi ya kuandika
- Eleza kwa nini daima\((−\sqrt{n})^2\) ni chanya, kwa\(n \ge 0\).
- Eleza kwa nini daima\(−(\sqrt{n})^2\) ni hasi, kwa\(n \ge 0\).
- Jibu
-
- wakati wa mraba hasi, inakuwa chanya
- tangu hasi ni pamoja na katika mabano, si squared, na bado hasi
Tumia muundo wa mraba wa binomial ili kurahisisha\((3+\sqrt{2})^2\). Eleza hatua zako zote.
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
ⓑ Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?


